Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T04:00:38.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Shintani descent for algebraic groups and almost characters of unipotent groups

Part of: Representation theory of groups

Published online by Cambridge University Press:  01 June 2016

Tanmay Deshpande
Tanmay Deshpande*
Affiliation:
School of Mathematics, TIFR, Homi Bhabha Road, Colaba, Mumbai 400005, India email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we extend the notion of Shintani descent to general (possibly disconnected) algebraic groups defined over a finite field 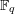$\mathbb{F}_{q}$. For this, it is essential to treat all the pure inner 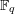$\mathbb{F}_{q}$-rational forms of the algebraic group at the same time. We prove that the notion of almost characters (introduced by Shoji using Shintani descent) is well defined for any neutrally unipotent algebraic group, i.e. an algebraic group whose neutral connected component is a unipotent group. We also prove that these almost characters coincide with the ‘trace of Frobenius’ functions associated with Frobenius-stable character sheaves on neutrally unipotent groups. In the course of the proof, we also prove that the modular categories that arise from Boyarchenko and Drinfeld’s theory of character sheaves on neutrally unipotent groups are in fact positive integral, confirming a conjecture due to Drinfeld.

Keywords

character sheavesShintani descent

MSC classification

Primary: 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 8 , August 2016 , pp. 1697 - 1724
Copyright
© The Author 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boyarchenko, M., Character sheaves and characters of unipotent groups over finite fields , Amer. J. Math. Soc. 135 (2013), 663–719.CrossRefGoogle Scholar
Boyarchenko, M. and Drinfeld, V., Character sheaves on unipotent groups in positive characteristic: foundations , Selecta Math. 20 (2014), 125–235, doi:10.1007/s00029-013-0133-7.CrossRefGoogle Scholar
Deshpande, T., Heisenberg idempotents on unipotent groups , Math. Res. Lett. 17 (2010), 415–434.CrossRefGoogle Scholar
Deshpande, T., Modular categories associated with unipotent groups , Selecta Math. 20 (2014), 285–313, doi:10.1007/s00029-013-0126-6.CrossRefGoogle Scholar
Deshpande, T., Crossed $S$ -matrices and character sheaves on unipotent groups, Preprint (2014), arXiv:1410.3274.Google Scholar
Drinfeld, V., Gelaki, S., Nikshych, D. and Ostrik, V., On braided fusion categories I , Selecta Math. 16 (2010), 1–119.Google Scholar
Etingof, P., Nikshych, D. and Ostrik, V., Quantum Topol. 1 (2010), 209–273.Google Scholar
Schaumann, G., Traces on module categories over fusion categories , J. Algebra 379 (2013), 382–425.CrossRefGoogle Scholar
Shintani, T., Two remarks on irreducible characters of finite general linear groups , J. Math. Soc. Japan 28 (1976), 396–414.Google Scholar
Shoji, T., Shintani descent for algebraic groups over a finite field, I , J. Algebra 145 (1992), 468–524.Google Scholar