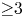Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Addington, Nicolas
Bragg, Daniel
and
Petrov, Alexander
2023.
Hodge numbers are not derived invariants in positive characteristic.
Mathematische Annalen,
Vol. 387,
Issue. 1-2,
p.
847.