Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Campana, Frédéric
and
Claudon, Benoît
2016.
Quelques propriétés de stabilité des variétés spéciales.
Mathematische Zeitschrift,
Vol. 283,
Issue. 1-2,
p.
581.
Cao, Junyan
and
Păun, Mihai
2017.
Kodaira dimension of algebraic fiber spaces over abelian varieties.
Inventiones mathematicae,
Vol. 207,
Issue. 1,
p.
345.
Claudon, Benoît
2018.
Smooth families of tori and linear Kähler groups.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 27,
Issue. 3,
p.
477.
Claudon, Benoît
Höring, Andreas
and
Lin, Hsueh-Yung
2019.
The fundamental group of compact Kähler
threefolds.
Geometry & Topology,
Vol. 23,
Issue. 7,
p.
3233.
Papadima, Stefan
and
Suciu, Alexander I.
2020.
RANK TWO TOPOLOGICAL AND INFINITESIMAL EMBEDDED JUMP LOCI OF QUASI-PROJECTIVE MANIFOLDS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 19,
Issue. 2,
p.
451.
Greb, Daniel
Kebekus, Stefan
and
Peternell, Thomas
2021.
Projectively flat klt varieties.
Journal de l’École polytechnique — Mathématiques,
Vol. 8,
Issue. ,
p.
1005.
Claudon, Benoît
Graf, Patrick
Guenancia, Henri
and
Naumann, Philipp
2022.
Kähler spaces with zero first Chern class: Bochner principle, Albanese map and fundamental groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 786,
p.
245.
Pereira, Jorge Vitório
Rousseau, Erwan
and
Touzet, Frédéric
2022.
Numerically non-special varieties.
Compositio Mathematica,
Vol. 158,
Issue. 6,
p.
1428.
Liu, Jie
Ou, Wenhao
and
Yang, Xiaokui
2022.
Projective manifolds whose tangent bundle contains a strictly nef subsheaf.
Journal of Algebraic Geometry,
Vol. 33,
Issue. 1,
p.
1.
Javanpeykar, Ariyan
and
Rousseau, Erwan
2022.
Albanese Maps and Fundamental Groups of Varieties With Many Rational Points Over Function Fields.
International Mathematics Research Notices,
Vol. 2022,
Issue. 24,
p.
19354.
Brunebarbe, Yohan
and
Maculan, Marco
2023.
Counting integral points of bounded height on varieties with large fundamental group.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Bei, Francesco
Diverio, Simone
Eyssidieux, Philippe
and
Trapani, Stefano
2024.
Weakly Kähler hyperbolic manifolds and the Green–Griffiths–Lang conjecture.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Liu, Jie
Ou, Wenhao
Wang, Juanyong
Yang, Xiaokui
and
Zhong, Guolei
2024.
Algebraic fibre spaces with strictly nef relative anti‐log canonical divisor.
Journal of the London Mathematical Society,
Vol. 109,
Issue. 6,
Druel, Stéphane
2024.
Projectively flat log smooth pairs.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 33,
Issue. 3,
p.
611.
Druel, Stéphane
2025.
PROJECTIVELY FLAT FOLIATIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 24,
Issue. 3,
p.
763.
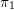 ${\it\pi}_{1}$of compact Kähler manifolds, J. Reine Angew. Math. 472 (1996), 139–156]. Enfin nous étendons au cas kählérien les résultats généraux de convexité holomorphe pour les revêtements associés connus dans le cas projectif.
${\it\pi}_{1}$of compact Kähler manifolds, J. Reine Angew. Math. 472 (1996), 139–156]. Enfin nous étendons au cas kählérien les résultats généraux de convexité holomorphe pour les revêtements associés connus dans le cas projectif.

