Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T14:35:37.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Pin(2)-equivariant Seiberg–Witten Floer homology of Seifert fibrations

Part of: Low-dimensional topology

Published online by Cambridge University Press:  09 December 2019

Matthew Stoffregen
Matthew Stoffregen*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA02142, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the 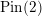$\text{Pin}(2)$-equivariant Seiberg–Witten Floer homology of Seifert rational homology three-spheres in terms of their Heegaard Floer homology. As a result of this computation, we prove Manolescu’s conjecture that 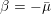$\unicode[STIX]{x1D6FD}=-\bar{\unicode[STIX]{x1D707}}$ for Seifert integral homology three-spheres. We show that the Manolescu invariants 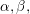$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},$ and 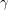$\unicode[STIX]{x1D6FE}$ give new obstructions to homology cobordisms between Seifert fiber spaces, and that many Seifert homology spheres $\unicode[STIX]{x1D6F4}(a_{1},\ldots ,a_{n})$ are not homology cobordant to any 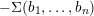$-\unicode[STIX]{x1D6F4}(b_{1},\ldots ,b_{n})$. We then use the same invariants to give an example of an integral homology sphere not homology cobordant to any Seifert fiber space. We also show that the 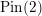$\text{Pin}(2)$-equivariant Seiberg–Witten Floer spectrum provides homology cobordism obstructions distinct from 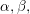$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},$ and 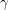$\unicode[STIX]{x1D6FE}$. In particular, we identify an 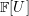$\mathbb{F}[U]$-module called connected Seiberg–Witten Floer homology, whose isomorphism class is a homology cobordism invariant.

Keywords

monopole Floer homologyhomology cobordismSeifert spaces

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 2 , February 2020 , pp. 199 - 250
Copyright
© The Author 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

MS was supported by NSF Grant DMS-1702532.

References

Borodzik, M. and Némethi, A., Heegaard–Floer homologies of (+1) surgeries on torus knots, Acta Math. Hungar. 139 (2013), 303–319.CrossRefGoogle Scholar
Can, M. B. and Karakurt, Ç., Calculating Heegaard–Floer homology by counting lattice points in tetrahedra, Acta Math. Hungar. 144 (2014), 43–75.CrossRefGoogle Scholar
Colin, V., Ghiggini, P. and Honda, K., Equivalence of Heegaard Floer homology and embedded contact homology via open book decompositions, Proc. Natl Acad. Sci. USA 108 (2011), 8100–8105.CrossRefGoogle ScholarPubMed
Conley, C., Isolated invariant sets and the Morse index, CBMS Regional Conference Series in Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 1978).CrossRefGoogle Scholar
Fintushel, R. and Stern, R. J., Pseudofree orbifolds, Ann. of Math. (2) 122 (1985), 335–364.CrossRefGoogle Scholar
Floer, A., A refinement of the Conley index and an application to the stability of hyperbolic invariant sets, Ergodic Theory Dynam. Systems 7 (1987), 93–103.CrossRefGoogle Scholar
Fukumoto, Y., Furuta, M. and Ue, M., W-invariants and Neumann–Siebenmann invariants for Seifert homology 3-spheres, Topol. Appl. 116 (2001), 333–369.CrossRefGoogle Scholar
Galewski, D. E. and Stern, R. J., Classification of simplicial triangulations of topological manifolds, Ann. of Math. (2) 111 (1980), 1–34.CrossRefGoogle Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Equivariant cohomology, Koszul duality, and the localization theorem, Invent. Math. 131 (1998), 25–83.CrossRefGoogle Scholar
Kronheimer, P. and Mrowka, T., Monopoles and three-manifolds, New Mathematical Monographs, vol. 10 (Cambridge University Press, Cambridge, 2007).CrossRefGoogle Scholar
Kutluhan, C., Lee, Y.-J. and Taubes, C. H., HF $=$ HM I: Heegaard Floer homology and Seiberg–Witten Floer homology, Preprint (2010), arXiv:1007.1979.Google Scholar
Lidman, T. and Manolescu, C., The equivalence of two Seiberg–Witten Floer homologies, Astérisque 399 (2018).Google Scholar
Lin, F., The surgery exact triangle in Pin(2)-monopole Floer homology, Algebr. Geom. Topol. 17 (2017), 2915–2960.CrossRefGoogle Scholar
Lin, F., A Morse–Bott approach to monopole Floer homology and the Triangulation conjecture, Mem. Amer. Math. Soc. 255(1221) (2018).Google Scholar
Manolescu, C., Seiberg–Witten–Floer stable homotopy type of three-manifolds with b 1 = 0, Geom. Topol. 7 (2003), 889–932 (electronic).CrossRefGoogle Scholar
Manolescu, C., The Conley index, gauge theory, and triangulations, J. Fixed Point Theory Appl. 13 (2013), 431–457.CrossRefGoogle Scholar
Manolescu, C., On the intersection forms of spin four-manifolds with boundary, Math. Ann. 359 (2014), 695–728.CrossRefGoogle Scholar
Manolescu, C., Pin(2)-equivariant Seiberg–Witten Floer homology and the triangulation conjecture, J. Amer. Math. Soc. 29 (2016), 147–176.CrossRefGoogle Scholar
Matumoto, T., Triangulation of manifolds, in Algebraic and geometric topology, part 2, Proc. Sympos. Pure Math., Stanford, CA, 1976, Proceedings of Symposia in Pure Mathematics, vol. 32 (American Mathematical Society, Providence, RI, 1978), 3–6.Google Scholar
Mrowka, T., Ozsváth, P. and Yu, B., Seiberg–Witten monopoles on Seifert fibered spaces, Comm. Anal. Geom. 5 (1997), 685–791.CrossRefGoogle Scholar
Némethi, A., On the Ozsváth–Szabó invariant of negative definite plumbed 3-manifolds, Geom. Topol. 9 (2005), 991–1042.CrossRefGoogle Scholar
Némethi, A., Graded roots and singularities, in Singularities in geometry and topology (World Scientific, Hackensack, NJ, 2007), 394–463.CrossRefGoogle Scholar
Neumann, W. D., An invariant of plumbed homology spheres, in Topology Symposium Siegen 1979, Lecture Notes in Mathematics, vol. 788 (Springer, Berlin, 1980), 125–144.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Absolutely graded Floer homologies and intersection forms for four-manifolds with boundary, Adv. Math. 173 (2003), 179–261.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., On the Floer homology of plumbed three-manifolds, Geom. Topol. 7 (2003), 185–224 (electronic).CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and topological invariants for closed three-manifolds, Ann. of Math. (2) 159 (2004), 1027–1158.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and three-manifold invariants: properties and applications, Ann. of Math. (2) 159 (2004), 1159–1245.CrossRefGoogle Scholar
Pruszko, A. M., The Conley index for flows preserving generalized symmetries, in Conley index theory, Warsaw, 1997, Banach Center Publications, vol. 47 (Polish Academy of Sciences, Warsaw, 1999), 193–217.Google Scholar
Ruberman, D. and Saveliev, N., The 𝜇 -invariant of Seifert fibered homology spheres and the Dirac operator, Geom. Dedicata 154 (2011), 93–101.CrossRefGoogle Scholar
Saveliev, N., Floer homology and invariants of homology cobordism, Internat. J. Math. 9 (1998), 885–919.CrossRefGoogle Scholar
Saveliev, N., Floer homology of Brieskorn homology spheres, J. Differential Geom. 53 (1999), 15–87.CrossRefGoogle Scholar
Saveliev, N., Fukumoto–Furuta invariants of plumbed homology 3-spheres, Pacific J. Math. 205 (2002), 465–490.CrossRefGoogle Scholar
Siebenmann, L., On vanishing of the Rohlin invariant and nonfinitely amphicheiral homology 3-spheres, in Topology Symposium Siegen 1979, Lecture Notes in Mathematics, vol. 788 (Springer, Berlin, 1980), 172–222.CrossRefGoogle Scholar
Taubes, C. H., The Seiberg–Witten equations and the Weinstein conjecture, Geom. Topol. 11 (2007), 2117–2202.CrossRefGoogle Scholar
tom Dieck, T., Transformation groups, De Gruyter Studies in Mathematics, vol. 8 (De Gruyter, Berlin, 1987).CrossRefGoogle Scholar
Tweedy, E., Heegaard Floer homology and several families of Brieskorn spheres, Topology Appl. 160 (2013), 620–632.CrossRefGoogle Scholar
Waner, S., Equivariant homotopy theory and Milnor’s theorem, Trans. Amer. Math. Soc. 258 (1980), 351–368.Google Scholar
Weibel, C. A., An introduction to homological algebra, in Cambridge Studies in Advanced Mathematics, vol 38 (Cambridge University Press, Cambridge, 1994).Google Scholar