Article contents
The Pila–Wilkie theorem for subanalytic families: a complex analytic approach
Published online by Cambridge University Press: 27 July 2017
Abstract
We present a complex analytic proof of the Pila–Wilkie theorem for subanalytic sets. In particular, we replace the use of 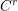 $C^{r}$-smooth parametrizations by a variant of Weierstrass division. As a consequence we are able to apply the Bombieri–Pila determinant method directly to analytic families without limiting the order of smoothness by a
$C^{r}$-smooth parametrizations by a variant of Weierstrass division. As a consequence we are able to apply the Bombieri–Pila determinant method directly to analytic families without limiting the order of smoothness by a 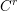 $C^{r}$ parametrization. This technique provides the key inductive step for our recent proof (in a closely related preprint) of the Wilkie conjecture for sets definable using restricted elementary functions. As an illustration of our approach we prove that the rational points of height
$C^{r}$ parametrization. This technique provides the key inductive step for our recent proof (in a closely related preprint) of the Wilkie conjecture for sets definable using restricted elementary functions. As an illustration of our approach we prove that the rational points of height 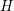 $H$ in a compact piece of a complex-analytic set of dimension
$H$ in a compact piece of a complex-analytic set of dimension 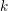 $k$ in
$k$ in 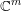 $\mathbb{C}^{m}$ are contained in
$\mathbb{C}^{m}$ are contained in 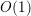 $O(1)$ complex-algebraic hypersurfaces of degree
$O(1)$ complex-algebraic hypersurfaces of degree 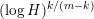 $(\log H)^{k/(m-k)}$. This is a complex-analytic analog of a recent result of Cluckers, Pila, and Wilkie for real subanalytic sets.
$(\log H)^{k/(m-k)}$. This is a complex-analytic analog of a recent result of Cluckers, Pila, and Wilkie for real subanalytic sets.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 4
- Cited by


