Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T05:35:26.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Paraboline variation over 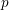$p$-adic families of $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  19 January 2017

John Bergdall
John Bergdall*
Affiliation:
Department of Mathematics and Statistics, Boston University, 111 Cummington Mall, Boston, MA 02215, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the 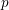$p$-adic variation of triangulations over 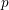$p$-adic families of 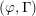$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules. In particular, we study certain canonical sub-filtrations of the pointwise triangulations and show that they extend to affinoid neighborhoods of crystalline points. This generalizes results of Kedlaya, Pottharst and Xiao and (independently) Liu in the case where one expects the entire triangulation to extend. We also study the ramification of weight parameters over natural 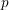$p$-adic families.

Keywords

(𝜑, 𝛤)-modulestrianguline representations

MSC classification

Primary: 11F80: Galois representations 11F85: $p$-adic theory, local fields
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F55: Other groups and their modular and automorphic forms (several variables)
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 1 , January 2017 , pp. 132 - 174
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellaïche, J., Critical p-adic L-functions , Invent. Math. 189 (2012), 1–60.Google Scholar
Bellaïche, J. and Chenevier, G., Families of Galois representations and Selmer groups, Astérisque, vol. 324 (Société Mathématique de France, 2009).Google Scholar
Bellovin, R., p-adic Hodge theory in rigid analytic families , Algebra Number Theory 9 (2015), 371–433.Google Scholar
Bergdall, J., Ordinary modular forms and companion points on the eigencurve , J. Number Theory 134 (2014), 226–239.Google Scholar
Berger, L., Représentations p-adiques et équations différentielles , Invent. Math. 148 (2002), 219–284.CrossRefGoogle Scholar
Berger, L., Équations différentielles p-adiques et (𝜙, N)-modules filtrés , in Représentations p-adiques de groupes p-adiques I: représentations galoisiennes et (𝜙, 𝛤)-modules, Astérisque, vol. 319 (Société Mathématique de France, 2008), 13–38.Google Scholar
Berkovich, V. G., Étale cohomology for non-Archimedean analytic spaces , Publ. Math. Inst. Hautes Études Sci. 78 (1994), 5–161; 1993.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis: a systematic approach to rigid analytic geometry, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261 (Springer, Berlin, 1984).Google Scholar
Bosch, S. and Lütkebohmert, W., Formal and rigid geometry. II. Flattening techniques , Math. Ann. 296 (1993), 403–429.Google Scholar
Breuil, C., Vers le socle localement analytique pour GL n II , Math. Ann. 361 (2015), 741–785.Google Scholar
Chenevier, G., On the infinite fern of Galois representations of unitary type , Ann. Sci. Éc. Norm. Supér. (4) 44 (2011), 963–1019.Google Scholar
Cherbonnier, F. and Colmez, P., Représentations p-adiques surconvergentes , Invent. Math. 133 (1998), 581–611.Google Scholar
Coleman, R. F. and Mazur, B., The eigencurve , in Galois representations in arithmetic algebraic geometry (Durham, 1996), London Mathematical Society Lecture Note Series, vol. 254 (Cambridge University Press, Cambridge, 1998), 1–113.Google Scholar
Colmez, P., Représentations triangulines de dimension 2 , in Représentations p-adiques de groupes p-adiques I: représentations galoisiennes et (𝜙, 𝛤)-modules, Astérisque, vol. 319 (Société Mathématique de France, 2008), 213–258.Google Scholar
Conrad, B., Irreducible components of rigid spaces , Ann. Inst. Fourier (Grenoble) 49 (1999), 473–541.Google Scholar
Ducros, A., Les espaces de Berkovich sont excellents , Ann. Inst. Fourier (Grenoble) 59 (2009), 1443–1552.CrossRefGoogle Scholar
Emerton, M., Local-global compatibility in the $p$ -adic Langlands programme for $\text{GL}_{2}/\mathbf{Q}$ , Preprint, www.math.uchicago.edu/∼emerton/pdffiles/lg.pdf.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux. I , in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 249–309.Google Scholar
Fontaine, J.-M. and Mazur, B., Geometric Galois representations , in Elliptic curves, modular forms, & Fermat’s last theorem (Hong Kong, 1993), Series on Number Theory, I (International Press, Cambridge, MA, 1995), 41–78.Google Scholar
Hansen, D., Universal eigenvarieties, trianguline Galois representations, and $p$ -adic Langlands functoriality, J. Reine Angew. Math., to appear, doi:10.1515/crelle-2014-0130.Google Scholar
Herr, L., Sur la cohomologie galoisienne des corps p-adiques , Bull. Soc. Math. France 126 (1998), 563–600.Google Scholar
Kedlaya, K. S., A p-adic local monodromy theorem , Ann. of Math. (2) 160 (2004), 93–184.Google Scholar
Kedlaya, K. S. and Liu, R., On families of 𝜑, 𝛤-modules , Algebra Number Theory 4 (2010), 943–967.Google Scholar
Kedlaya, K. S., Pottharst, J. and Xiao, L., Cohomology of arithmetic families of (𝜑, 𝛤)-modules , J. Amer. Math. Soc. 27 (2014), 1043–1115.Google Scholar
Kisin, M., Overconvergent modular forms and the Fontaine-Mazur conjecture , Invent. Math. 153 (2003), 373–454.Google Scholar
Liu, R., Cohomology and duality for (𝜙, 𝛤)-modules over the Robba ring , Int. Math. Res. Not. IMRN 2007 (2007), doi:10.1093/imrn/rnm150.Google Scholar
Liu, R., Triangulation of refined families , Comment. Math. Helv. 90 (2015), 831–904.Google Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8, second edition (Cambridge University Press, Cambridge, 1989); translated from the Japanese by M. Reid.Google Scholar
Mazur, B. and Wiles, A., On p-adic analytic families of Galois representations , Compositio Math. 59 (1986), 231–264.Google Scholar
Nakamura, K., Classification of two-dimensional split trianguline representations of p-adic fields , Compositio Math. 145 (2009), 865–914.Google Scholar
Schneider, P. and Teitelbaum, J., Algebras of p-adic distributions and admissible representations , Invent. Math. 153 (2003), 145–196.Google Scholar
Sen, S., The analytic variation of p-adic Hodge structure , Ann. of Math. (2) 127 (1988), 647–661.Google Scholar
Tan, F., Families of p-adic Galois Representations. ProQuest LLC, Ann Arbor, MI, 2011, PhD Thesis, Massachusetts Institute of Technology.Google Scholar
The Stacks Project Authors. Stacks project. http://stacks.math.columbia.edu, 2015.Google Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994).Google Scholar