Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T04:38:46.820Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Balmer spectrum for compact Lie groups

Part of: Homotopy theory

Published online by Cambridge University Press:  14 November 2019

Tobias Barthel ,
J. P. C. Greenlees  and
Markus Hausmann
Tobias Barthel
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 København Ø, Denmark email [email protected], [email protected]
J. P. C. Greenlees
Affiliation:
Warwick Mathematics Institute, Zeeman Building, Coventry CV4 7AL, UK email [email protected]
Markus Hausmann
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 København Ø, Denmark email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the Balmer spectrum of the category of finite 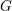$G$-spectra for a compact Lie group 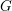$G$, extending the work for finite 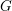$G$ by Strickland, Balmer–Sanders, Barthel–Hausmann–Naumann–Nikolaus–Noel–Stapleton and others. We give a description of the underlying set of the spectrum and show that the Balmer topology is completely determined by the inclusions between the prime ideals and the topology on the space of closed subgroups of 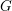$G$. Using this, we obtain a complete description of this topology for all abelian compact Lie groups and consequently a complete classification of thick tensor ideals. For general compact Lie groups we obtain such a classification away from a finite set of primes 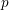$p$.

Keywords

equivariant spectrathick tensor idealsBalmer spectrumspace of subgroups

MSC classification

Primary: 55P42: Stable homotopy theory, spectra 55P91: Equivariant homotopy theory
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 1 , January 2020 , pp. 39 - 76
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany

2

Current address: Mathematical Institute, Rheinische Friedrich-Wilhelms-Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany

TB was supported by the Danish National Research Foundation Grant DNRF92 and the European Unions Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 751794. JPCG is grateful to the EPSRC for support from EP/P031080/1. MH was supported by the Danish National Research Foundation Grant DNRF92.

References

Arone, G., Iterates of the suspension map and Mitchell’s finite spectra with A k-free cohomology , Math. Res. Lett. 5 (1998), 485–496; MR 1653316.Google Scholar
Arone, G. and Lesh, K., Fixed points of coisotropic subgroups of $\unicode[STIX]{x1D6E4}_{k}$ on decomposition spaces, Preprint (2017), arXiv:1701.06070.Google Scholar
Arone, G. and Mahowald, M., The Goodwillie tower of the identity functor and the unstable periodic homotopy of spheres , Invent. Math. 135 (1999), 743–788; MR 1669268.Google Scholar
Balmer, P., The spectrum of prime ideals in tensor triangulated categories , J. Reine Angew. Math. 588 (2005), 149–168; MR 2196732.Google Scholar
Balmer, P., Spectra, spectra, spectra – tensor triangular spectra versus Zariski spectra of endomorphism rings , Algebr. Geom. Topol. 10 (2010), 1521–1563; MR 2661535.Google Scholar
Balmer, P. and Sanders, B., The spectrum of the equivariant stable homotopy category of a finite group , Invent. Math. 208 (2017), 283–326; MR 3621837.Google Scholar
Barthel, T., Hausmann, M., Naumann, N., Nikolaus, T., Noel, J. and Stapleton, N., The Balmer spectrum of the equivariant homotopy category of a finite abelian group , Invent. Math. 216 (2019), 215–240; MR 3935041.Google Scholar
Bousfield, A. K., On K (n)-equivalences of spaces , in Homotopy invariant algebraic structures (Baltimore, MD, 1998), Contemporary Mathematics, vol. 239 (American Mathematical Society, Providence, RI, 1999), 85–89; MR 1718077.Google Scholar
Bredon, G., Introduction to compact transformation groups, Pure and Applied Mathematics, vol. 46 (Academic Press, New York–London, 1972); MR 0413144.Google Scholar
Bröcker, T. and tom Dieck, T., Representations of compact Lie groups, Graduate Texts in Mathematics, vol. 98 (Springer, New York, 1985); MR 781344.Google Scholar
Devinatz, E. S., Hopkins, M. J. and Smith, J. H., Nilpotence and stable homotopy theory. I , Ann. of Math. (2) 128 (1988), 207–241; MR 960945.Google Scholar
tom Dieck, T., Bordism of G-manifolds and integrality theorems , Topology 9 (1970), 345–358; MR 0266241.Google Scholar
tom Dieck, T., The Burnside ring and equivariant stable homotopy, Lecture Notes by Michael C. Bix (Department of Mathematics, University of Chicago, Chicago, IL, 1975); MR 0423389.Google Scholar
tom Dieck, T., The Burnside ring of a compact Lie group. I , Math. Ann. 215 (1975), 235–250; MR 0394711.Google Scholar
tom Dieck, T., A finiteness theorem for the Burnside ring of a compact Lie group , Compositio Math. 35 (1977), 91–97; MR 0474344.Google Scholar
tom Dieck, T., Transformation groups and representation theory, Lecture Notes in Mathematics, vol. 766 (Springer, Berlin, 1979); MR 551743.Google Scholar
Dress, A., A characterisation of solvable groups , Math. Z. 110 (1969), 213–217; MR 0248239.Google Scholar
Fausk, H., Survey on the Burnside ring of compact Lie groups , J. Lie Theory 18 (2008), 351–368; MR 2431120.Google Scholar
Fausk, H. and Oliver, B., Continuity of 𝜋-perfection for compact Lie groups , Bull. Lond. Math. Soc. 37 (2005), 135–140; MR 2106728.Google Scholar
Greenlees, J. P. C. and May, J. P., Equivariant stable homotopy theory , in Handbook of algebraic topology (North-Holland, Amsterdam, 1995), 277–323; MR 1361893.Google Scholar
Greenlees, J. P. C. and May, J. P., Generalized Tate cohomology , Mem. Amer. Math. Soc. 113 (1995), MR 1230773 (96e:55006).Google Scholar
Greenlees, J. P. C., The Balmer spectrum of rational equivariant cohomology theories , J. Pure Appl. Algebra 223 (2019), 2845–2871; MR 3912951.Google Scholar
Greenlees, J. P. C. and Sadofsky, H., The Tate spectrum of v n-periodic complex oriented theories , Math. Z. 222 (1996), 391–405; MR 1400199.Google Scholar
Hopkins, M. J. and Smith, J. H., Nilpotence and stable homotopy theory. II , Ann. of Math. (2) 148 (1998), 1–49; MR 1652975.Google Scholar
Hovey, M., Palmieri, J. H. and Strickland, N. P., Axiomatic stable homotopy theory , Mem. Amer. Math. Soc. 128 (1997), MR 1388895.Google Scholar
Kelly, G., Basic concepts of enriched category theory, London Mathematical Society Lecture Note Series, vol. 64 (Cambridge University Press, Cambridge-New York, 1982); MR 651714.Google Scholar
Landweber, P., Conjugations on complex manifolds and equivariant homotopy of MU , Bull. Amer. Math. Soc. 74 (1968), 271–274; MR 0222890.Google Scholar
Lewis, L. G. Jr., May, J. P., Steinberger, M. and McClure, J. E., Equivariant stable homotopy theory, Lecture Notes in Mathematics, vol. 1213 (Springer, Berlin, 1986), with contributions by J. E. McClure; MR 866482.Google Scholar
May, J. P., Equivariant homotopy and cohomology theory, CBMS Regional Conference Series in Mathematics, vol. 91 (American Mathematical Society, Providence, RI, 1996); MR 1413302.Google Scholar
Mandell, M. A. and May, J. P., Equivariant orthogonal spectra and S-modules , Mem. Amer. Math. Soc. 159 (2002), MR 1922205.Google Scholar
Mathew, A., Naumann, N. and Noel, J., Nilpotence and descent in equivariant stable homotopy theory , Adv. Math. 305 (2017), 994–1084; MR 3570153.Google Scholar
Mitchell, S., Finite complexes with A (n)-free cohomology , Topology 24 (1985), 227–246; MR 793186 (86k:55007).Google Scholar
Montgomery, D. and Zippin, L., A theorem on Lie groups , Bull. Amer. Math. Soc. 48 (1942), 448–452; MR 0006545.Google Scholar
Orlik, P. and Terao, H., Arrangements of hyperplanes, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 300 (Springer, Berlin), 1992; MR 1217488.Google Scholar
Ravenel, D., Localization with respect to certain periodic homology theories , Amer. J. Math. 106 (1984), 351–414; MR 737778.Google Scholar
Schwede, S., Global homotopy theory, New Mathematical Monographs, vol. 34 (Cambridge University Press, Cambridge, 2018); MR 3838307.Google Scholar
Sinha, D. P., Computations of complex equivariant bordism rings , Amer. J. Math. 123 (2001), 577–605; MR 1844571.Google Scholar