Article contents
On higher direct images of convergent isocrystals
Published online by Cambridge University Press: 25 September 2019
Abstract
Let 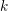 $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic 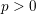 $p>0$ and let
$p>0$ and let 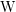 $\operatorname{W}$ be the ring of Witt vectors of
$\operatorname{W}$ be the ring of Witt vectors of 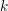 $k$. In this article, we give a new proof of the Frobenius descent for convergent isocrystals on a variety over
$k$. In this article, we give a new proof of the Frobenius descent for convergent isocrystals on a variety over 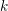 $k$ relative to
$k$ relative to 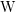 $\operatorname{W}$. This proof allows us to deduce an analogue of the de Rham complexes comparison theorem of Berthelot [
$\operatorname{W}$. This proof allows us to deduce an analogue of the de Rham complexes comparison theorem of Berthelot [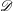 $\mathscr{D}$-modules arithmétiques. II. Descente par Frobenius, Mém. Soc. Math. Fr. (N.S.) 81 (2000)] without assuming a lifting of the Frobenius morphism. As an application, we prove a version of Berthelot’s conjecture on the preservation of convergent isocrystals under the higher direct image by a smooth proper morphism of
$\mathscr{D}$-modules arithmétiques. II. Descente par Frobenius, Mém. Soc. Math. Fr. (N.S.) 81 (2000)] without assuming a lifting of the Frobenius morphism. As an application, we prove a version of Berthelot’s conjecture on the preservation of convergent isocrystals under the higher direct image by a smooth proper morphism of 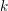 $k$-varieties.
$k$-varieties.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2019
References
- 2
- Cited by


