Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goldring, Wushi
and
Koskivirta, Jean-Stefan
2018.
Automorphic vector bundles with global sections on -schemes.
Compositio Mathematica,
Vol. 154,
Issue. 12,
p.
2586.
Boxer, George
Calegari, Frank
Gee, Toby
and
Pilloni, Vincent
2021.
Abelian surfaces over totally real fields are potentially modular.
Publications mathématiques de l'IHÉS,
Vol. 134,
Issue. 1,
p.
153.
Goren, Eyal
and
de Shalit, Ehud
2023.
Foliations on Shimura varieties in positive characteristic.
Journal of Algebraic Geometry,
Vol. 33,
Issue. 3,
p.
401.
Diamond, Fred
2023.
GEOMETRIC WEIGHT-SHIFTING OPERATORS ON HILBERT MODULAR FORMS IN CHARACTERISTIC p.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 4,
p.
1871.
Diamond, Fred
and
Kassaei, Payman L
2023.
The Cone of Minimal Weights for Mod p Hilbert Modular Forms.
International Mathematics Research Notices,
Vol. 2023,
Issue. 14,
p.
12148.
Imai, Naoki
and
Koskivirta, Jean-Stefan
2024.
Partial Hasse invariants for Shimura varieties of Hodge-type.
Advances in Mathematics,
Vol. 440,
Issue. ,
p.
109518.
Deo, Shaunak V.
Dimitrov, Mladen
and
Wiese, Gabor
2024.
Unramifiedness of weight 1 Hilbert Hecke algebras.
Algebra & Number Theory,
Vol. 18,
Issue. 8,
p.
1465.
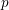 $p$
$p$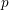 $p$ Hilbert modular forms associated to a totally real field of degree
$p$ Hilbert modular forms associated to a totally real field of degree 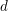 $d$ in which
$d$ in which 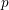 $p$ is unramified. We prove that every such form arises by multiplication by partial Hasse invariants from one whose weight (a
$p$ is unramified. We prove that every such form arises by multiplication by partial Hasse invariants from one whose weight (a 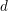 $d$-tuple of integers) lies in a certain cone contained in the set of non-negative weights, answering a question of Andreatta and Goren. The proof is based on properties of the Goren–Oort stratification on mod
$d$-tuple of integers) lies in a certain cone contained in the set of non-negative weights, answering a question of Andreatta and Goren. The proof is based on properties of the Goren–Oort stratification on mod 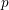 $p$ Hilbert modular varieties established by Goren and Oort, and Tian and Xiao.
$p$ Hilbert modular varieties established by Goren and Oort, and Tian and Xiao.