Article contents
Localization and nilpotent spaces in 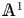 ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
Published online by Cambridge University Press: 27 May 2022
Abstract
For a subring 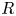 $R$ of the rational numbers, we study
$R$ of the rational numbers, we study 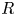 $R$-localization functors in the local homotopy theory of simplicial presheaves on a small site and then in
$R$-localization functors in the local homotopy theory of simplicial presheaves on a small site and then in 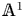 ${\mathbb {A}}^1$-homotopy theory. To this end, we introduce and analyze two notions of nilpotence for spaces in
${\mathbb {A}}^1$-homotopy theory. To this end, we introduce and analyze two notions of nilpotence for spaces in 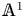 ${\mathbb {A}}^1$-homotopy theory, paying attention to future applications for vector bundles. We show that
${\mathbb {A}}^1$-homotopy theory, paying attention to future applications for vector bundles. We show that 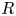 $R$-localization behaves in a controlled fashion for the nilpotent spaces we consider. We show that the classifying space
$R$-localization behaves in a controlled fashion for the nilpotent spaces we consider. We show that the classifying space 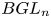 $BGL_n$ is
$BGL_n$ is 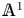 ${\mathbb {A}}^1$-nilpotent when
${\mathbb {A}}^1$-nilpotent when 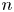 $n$ is odd, and analyze the (more complicated) situation where
$n$ is odd, and analyze the (more complicated) situation where 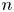 $n$ is even as well. We establish analogs of various classical results about rationalization in the context of
$n$ is even as well. We establish analogs of various classical results about rationalization in the context of 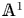 ${\mathbb {A}}^1$-homotopy theory: if
${\mathbb {A}}^1$-homotopy theory: if 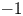 $-1$ is a sum of squares in the base field,
$-1$ is a sum of squares in the base field, 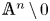 ${\mathbb {A}}^n \,{\setminus}\, 0$ is rationally equivalent to a suitable motivic Eilenberg–Mac Lane space, and the special linear group decomposes as a product of motivic spheres.
${\mathbb {A}}^n \,{\setminus}\, 0$ is rationally equivalent to a suitable motivic Eilenberg–Mac Lane space, and the special linear group decomposes as a product of motivic spheres.
Keywords
- Type
- Research Article
- Information
- Copyright
- © 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
AA was partially supported by National Science Foundation Awards DMS-1254892 and DMS-1802060. MJH was partially supported by National Science Foundation Awards DMS-0906194, DMS-1510417 and DMS-1810917.
References
- 1
- Cited by



