No CrossRef data available.
Article contents
Local monodromy of Drinfeld modules
Published online by Cambridge University Press: 03 December 2024
Abstract
Compared with algebraic varieties the local monodromy of Drinfeld modules appears to be hopelessly complex: the image of the wild inertia subgroup under Tate module representations is infinite save for the case of potential good reduction. Nonetheless, we show that Tate modules of Drinfeld modules are ramified in a limited way: the image of a sufficiently deep ramification subgroup is trivial. This leads to a new invariant, the local conductor of a Drinfeld module. We establish an upper bound on the conductor in terms of the volume of the period lattice. As an intermediate step we develop a theory of normed lattices in function field arithmetic including the notion of volume. We relate normed lattices to vector bundles on projective curves. With the aid of Castelnuovo–Mumford regularity this implies a volume bound on norms of lattice generators, and the conductor inequality follows. Last but not least we describe the image of inertia for Drinfeld modules with period lattices of rank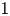 
$1$. Just as in the theory of local 
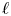$\ell$-adic Galois representations this image is commensurable with a commutative unipotent algebraic subgroup. However, in the case of Drinfeld modules such a subgroup can be a product of several copies of 
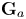$\mathbf {G}_a$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
In memory of my father Leonid.
References
Asayama, T. and Huang, M., Ramification of Tate modules for rank 
$2$ Drinfeld modules, Tohoku Math. J. 76 (2024), 445–481.CrossRefGoogle Scholar
$2$ Drinfeld modules, Tohoku Math. J. 76 (2024), 445–481.CrossRefGoogle ScholarBosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften, vol. 261. Springer, Berlin, 1984).CrossRefGoogle Scholar
Bourbaki, N., Espaces vectoriels topologiques. Chapitres 1 à 5. Éléments de mathématique (Masson, Paris, 1981).Google Scholar
Grothendieck, A. and Raynaud, M., Modèles de Néron et monodromie, in Groupes de monodromie en géométrie algébrique (SGA 7 1), Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, Heidelberg, 1972), 313–523.CrossRefGoogle Scholar
Huang, M., On successive minimal bases of division points of Drinfeld modules, Taiwanese J. Math. 28 (2024), 249–295.CrossRefGoogle Scholar
Papikian, M., Drinfeld Modules, Graduate Texts in Mathematics, vol. 296 (Springer, Cham, 2023).CrossRefGoogle Scholar
Poonen, B., Local height functions and the Mordell–Weil theorem for Drinfeld modules, Compos. Math. 97 (1995), 349–368.Google Scholar
Raynaud, M., Variétés abéliennes et géométrie rigide, in Actes, Congrès Intern. Math., 1970, Tome 1 (Gauthier-Villars Éditeur, Paris, 1971), 473–477.Google Scholar
Serre, J.-P., Local class field theory, in Algebraic number theory (Thompson, Washington, DC, 1967), 128–161.Google Scholar
Serre, J.-P., Corps locaux, 3ème édition, corrigée, Publications de l'Institut de Mathématique de l'Université de Nancago, vol. VIII (Hermann, Paris, 1968).Google Scholar
Silverman, J. H., The arithmetic of elliptic curves, second edition, Graduate Texts in Mathematics, vol. 106 (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Taguchi, Y., Semi-simplicity of the Galois representations attached to Drinfeld modules over fields of “infinite characteristic”, J. Number Theory 44 (1993), 292–314.CrossRefGoogle Scholar
Takahashi, T., Good reduction of elliptic modules, J. Math. Soc. Japan 34 (1982), 475–487.CrossRefGoogle Scholar
Thomas, L., Ramification groups in Artin–Schreier–Witt extensions, J. Théor. Nombres Bordeaux 17 (2005), 689–720.CrossRefGoogle Scholar