Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang-Erickson, Carl
2018.
Algebraic families of Galois representations and potentially semi-stable pseudodeformation rings.
Mathematische Annalen,
Vol. 371,
Issue. 3-4,
p.
1615.
Lan, Kai-Wen
and
Stroh, Benoît
2018.
Nearby cycles of automorphic étale sheaves.
Compositio Mathematica,
Vol. 154,
Issue. 1,
p.
80.
Haines, Thomas
2018.
Dualities for root systems with automorphisms and applications to non-split groups.
Representation Theory of the American Mathematical Society,
Vol. 22,
Issue. 1,
p.
1.
RICHARZ, TIMO
and
SCHOLBACH, JAKOB
2020.
THE INTERSECTION MOTIVE OF THE MODULI STACK OF SHTUKAS.
Forum of Mathematics, Sigma,
Vol. 8,
Issue. ,
Haines, Thomas
and
Richarz, Timo
2020.
The test function conjecture for parahoric local models.
Journal of the American Mathematical Society,
Vol. 34,
Issue. 1,
p.
135.
He, Xuhua
Pappas, Georgios
and
Rapoport, Michael
2020.
Good and semi-stable reductions of Shimura varieties.
Journal de l’École polytechnique — Mathématiques,
Vol. 7,
Issue. ,
p.
497.
Haines, Thomas J.
and
Richarz, Timo
2020.
The test function conjecture for local models of Weil-restricted groups.
Compositio Mathematica,
Vol. 156,
Issue. 7,
p.
1348.
Liu, Shinan
2021.
Modèle local des schémas de Hilbert–Siegel
de niveau Γ1(p).
Algebra & Number Theory,
Vol. 15,
Issue. 7,
p.
1655.
Lourenço, João
2023.
Grassmanniennes affines tordues sur les entiers.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Fakhruddin, Najmuddin
Haines, Thomas
Lourenço, João
and
Richarz, Timo
2025.
Singularities of local models.
Mathematische Annalen,
Vol. 391,
Issue. 4,
p.
6205.
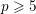 $p\geqslant 5$. We show that the local models are normal with special fiber reduced and study the monodromy action on the sheaves of nearby cycles. As a consequence, we prove a conjecture of Kottwitz that the semi-simple trace of Frobenius gives a central function in the parahoric Hecke algebra. We also introduce a notion of splitting model and use this to study the inertial action in the case of an unramified group.
$p\geqslant 5$. We show that the local models are normal with special fiber reduced and study the monodromy action on the sheaves of nearby cycles. As a consequence, we prove a conjecture of Kottwitz that the semi-simple trace of Frobenius gives a central function in the parahoric Hecke algebra. We also introduce a notion of splitting model and use this to study the inertial action in the case of an unramified group.