Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T13:11:10.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreducibility of polynomials over global fields is diophantine

Part of: Algebraic number theory: global fields Number theory: Connections with logic

Published online by Cambridge University Press:  08 March 2018

Philip Dittmann
Philip Dittmann*
Affiliation:
Mathematical Institute, University of Oxford, Woodstock Road, Oxford OX2 6GG, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a global field 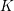$K$ and a positive integer $n$, we present a diophantine criterion for a polynomial in one variable of degree $n$ over 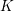$K$ not to have a root in 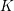$K$. This strengthens a result by Colliot-Thélène and Van Geel [Compositio Math. 151 (2015), 1965–1980] stating that the set of non-$n$th powers in a number field 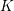$K$ is diophantine. We also deduce a diophantine criterion for a polynomial over 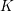$K$ of given degree in a given number of variables to be irreducible. Our approach is based on a generalisation of the quaternion method used by Poonen and Koenigsmann for first-order definitions of 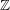$\mathbb{Z}$ in 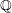$\mathbb{Q}$.

Keywords

central simple algebradefinabilitydiophantine set

MSC classification

Primary: 11U05: Decidability
Secondary: 11R52: Quaternion and other division algebras
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 4 , April 2018 , pp. 761 - 772
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cohen, S. D., Explicit theorems on generator polynomials , Finite Fields Appl. (2005), 337–357.Google Scholar
Colliot-Thélène, J.-L. and Van Geel, J., Le complémentaire des puissances n-ièmes dans un corps de nombres est un ensemble diophantien , Compositio Math. 151 (2015), 1965–1980.Google Scholar
Eisenträger, K., Integrality at a prime for global fields and the perfect closure of global fields of characteristic p > 2 , J. Number Theory 114 (2005), 170–181.Google Scholar
Eisenträger, K. and Morrison, T., Universally and existentially definable subsets of global fields, Math Res. Lett. (2017), to appear. Preprint (2016), arXiv:1609.09787 [math.NT].Google Scholar
Fein, B., Kantor, W. M. and Schacher, M., Relative Brauer groups II , J. Reine Angew. Math. 328 (1981), 39–57.Google Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology (Cambridge University Press, Cambridge, 2006).Google Scholar
Hodges, W., A shorter model theory (Cambridge University Press, Cambridge, 1997).Google Scholar
Jacobson, N., Finite-dimensional division algebras over fields (Springer, Berlin, 1996).CrossRefGoogle Scholar
Jacobson, N., Basic algebra II, second edn (Dover Publications, Mineola, NY, 2009).Google Scholar
Koenigsmann, J., Defining ℤ in ℚ , Ann. of Math. (2) 183 (2016), 73–93.CrossRefGoogle Scholar
Lang, S., Algebraic number theory (Addison-Wesley, Reading, MA; London, 1970).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, second edition (Springer, Berlin, Heidelberg, 2008).Google Scholar
Park, J., A universal first order formula defining the ring of integers in a number field , Math. Res. Lett. 20 (2013), 961–980.Google Scholar
Poonen, B., Characterizing integers among rational numbers with a universal-existential formula , Amer. J. Math. 131 (2009), 675–682.Google Scholar
Rosen, M., Number theory in function fields (Springer, New York, London, 2002).Google Scholar
Shlapentokh, A., Diophantine classes of holomorphy rings of global fields , J. Algebra 169 (1994), 139–175.Google Scholar