Article contents
Hopf-theoretic approach to motives of twisted flag varieties
Published online by Cambridge University Press: 29 April 2021
Abstract
Let 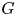 $G$ be a split semisimple algebraic group over a field and let
$G$ be a split semisimple algebraic group over a field and let 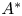 $A^*$ be an oriented cohomology theory in the Levine–Morel sense. We provide a uniform approach to the
$A^*$ be an oriented cohomology theory in the Levine–Morel sense. We provide a uniform approach to the 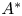 $A^*$-motives of geometrically cellular smooth projective
$A^*$-motives of geometrically cellular smooth projective 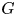 $G$-varieties based on the Hopf algebra structure of
$G$-varieties based on the Hopf algebra structure of 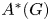 $A^*(G)$. Using this approach, we provide various applications to the structure of motives of twisted flag varieties.
$A^*(G)$. Using this approach, we provide various applications to the structure of motives of twisted flag varieties.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
Footnotes
The first author was supported by Laboratory of Modern Algebra and Applications, St. Petersburg State University, via a grant of the government of the Russian Federation for the state support of scientific research carried out under the supervision of leading scientists, agreement 14.W03.31.0030 dated 15.02.2018, by Young Russian Mathematics award and by RFBR grant 18-31-20044. The second author acknowledges the support of the SPP 1786 ‘Homotopy theory and algebraic geometry’ (DFG).
References
- 1
- Cited by



