Hostname: page-component-5cf477f64f-zrtmk Total loading time: 0 Render date: 2025-04-06T11:28:11.101Z Has data issue: false hasContentIssue false
  • English
  • Français

Homological vanishing for the Steinberg representation

Part of: Linear algebraic groups and related topics Connections with homological algebra and category theory

Published online by Cambridge University Press:  29 April 2018

Avner Ash ,
Andrew Putman  and
Steven V Sam
Avner Ash
Affiliation:
Department of Mathematics, Boston College, Chestnut Hill, MA 02467-3806, USA email [email protected]
Andrew Putman
Affiliation:
Department of Mathematics, University of Notre Dame, 279 Hurley Hall, Notre Dame, IN 46556, USA email [email protected]
Steven V Sam
Affiliation:
Department of Mathematics, University of Wisconsin, 480 Lincoln Dr., Madison, WI 53706-1325, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a field 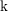$\text{k}$, we prove that the 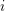$i$th homology of the groups 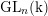$\operatorname{GL}_{n}(\text{k})$, 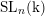$\operatorname{SL}_{n}(\text{k})$, 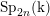$\operatorname{Sp}_{2n}(\text{k})$, 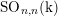$\operatorname{SO}_{n,n}(\text{k})$, and $\operatorname{SO}_{n,n+1}(\text{k})$ with coefficients in their Steinberg representations vanish for 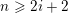$n\geqslant 2i+2$.

Keywords

Steinberg representationhomological stability

MSC classification

Primary: 20J05: Homological methods in group theory 20G10: Cohomology theory
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 6 , June 2018 , pp. 1111 - 1130
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borel, A. and Serre, J.-P., Corners and arithmetic groups , Comment. Math. Helv. 48 (1973), 436–491.CrossRefGoogle Scholar
Brown, K. S., Buildings (Springer, New York, NY, 1989).CrossRefGoogle Scholar
Brown, K. S., Cohomology of groups, Graduate Texts in Mathematics, vol. 87 corrected reprint of the 1982 original (Springer, New York, NY, 1994).Google Scholar
Church, T., Farb, B. and Putman, A., A stability conjecture for the unstable cohomology of SL n ℤ, mapping class groups, and Aut(F n ) , in Algebraic topology: applications and new directions, Contemporary Mathematics, vol. 620 (American Mathematical Society, Providence, RI, 2014), 55–70.Google Scholar
Church, T. and Putman, A., The codimension-one cohomology of  SL n ℤ , Geom. Topol. 21 (2017), 999–1032.CrossRefGoogle Scholar
Dwyer, W. G., Twisted homological stability for general linear groups , Ann. of Math. (2) 111 (1980), 239–251.CrossRefGoogle Scholar
Friedrich, N., Homological Stability of automorphism groups of quadratic modules and manifolds, Preprint (2016), arXiv:1612.04584v2.CrossRefGoogle Scholar
Humphreys, J. E., The Steinberg representation , Bull. Amer. Math. Soc. (N.S.) 16 (1987), 247–263.CrossRefGoogle Scholar
Lee, R. and Szczarba, R. H., On the homology and cohomology of congruence subgroups , Invent. Math. 33 (1976), 15–53.CrossRefGoogle Scholar
Maazen, H., Homology stability for the general linear group, PhD thesis, University of Utrecht (1979).Google Scholar
Macdonald, I. G., Symmetric functions and Hall polynomials, Oxford Mathematical Monographs, second edition (Oxford University Press, New York, NY, 1995).CrossRefGoogle Scholar
Malle, G. and Zalesskiĭ, A., Prime power degree representations of quasi-simple groups , Arch. Math. (Basel) 77 (2001), 461–468.CrossRefGoogle Scholar
Mirzaii, B. and van der Kallen, W., Homology stability for unitary groups , Doc. Math. 7 (2002), 143–166.CrossRefGoogle Scholar
Quillen, D., Finite generation of the groups K i of rings of algebraic integers , in Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Institute, Seattle, WA, 1972), Lecture Notes in Mathematics, vol. 341 (Springer, Berlin, 1972), 179–198.Google Scholar
Randal-Williams, O. and Wahl, N., Homological stability for automorphism groups, Preprint (2015), arXiv:1409.3541v3.Google Scholar
Reeder, M., The Steinberg module and the cohomology of arithmetic groups , J. Algebra 141 (1991), 287–315.CrossRefGoogle Scholar
van der Kallen, W., Homology stability for linear groups , Invent. Math. 60 (1980), 269–295.CrossRefGoogle Scholar