Article contents
Higher preprojective algebras, Koszul algebras, and superpotentials
Published online by Cambridge University Press: 01 February 2021
Abstract
In this article we study higher preprojective algebras, showing that various known results for ordinary preprojective algebras generalize to the higher setting. We first show that the quiver of the higher preprojective algebra is obtained by adding arrows to the quiver of the original algebra, and these arrows can be read off from the last term of the bimodule resolution of the original algebra. In the Koszul case, we are able to obtain the new relations of the higher preprojective algebra by differentiating a superpotential and we show that when our original algebra is 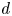 $d$-hereditary, all the relations come from the superpotential. We then construct projective resolutions of all simple modules for the higher preprojective algebra of a
$d$-hereditary, all the relations come from the superpotential. We then construct projective resolutions of all simple modules for the higher preprojective algebra of a 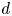 $d$-hereditary algebra. This allows us to recover various known homological properties of the higher preprojective algebras and to obtain a large class of almost Koszul dual pairs of algebras. We also show that when our original algebra is Koszul there is a natural map from the quadratic dual of the higher preprojective algebra to a graded trivial extension algebra.
$d$-hereditary algebra. This allows us to recover various known homological properties of the higher preprojective algebras and to obtain a large class of almost Koszul dual pairs of algebras. We also show that when our original algebra is Koszul there is a natural map from the quadratic dual of the higher preprojective algebra to a graded trivial extension algebra.
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
Footnotes
J.G. was supported first by the Japan Society for the Promotion of Science and then by the Engineering and Physical Sciences Research Council [grant number EP/G007497/1]. O.I. was supported by JSPS Grant-in-Aid for Scientific Research (B) 24340004, (B) 16H03923, (C) 18K03209 and (S) 15H05738.
References
- 8
- Cited by



