Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-02T20:33:41.413Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher index Fano varieties with finitely many birational automorphisms

Part of: Special varieties Birational geometry

Published online by Cambridge University Press:  02 December 2022

Nathan Chen  and
David Stapleton
Nathan Chen
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA [email protected]
David Stapleton
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A famous problem in birational geometry is to determine when the birational automorphism group of a Fano variety is finite. The Noether–Fano method has been the main approach to this problem. The purpose of this paper is to give a new approach to the problem by showing that in every positive characteristic, there are Fano varieties of arbitrarily large index with finite (or even trivial) birational automorphism group. To do this, we prove that these varieties admit ample and birationally equivariant line bundles. Our result applies the differential forms that Kollár produces on 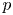$p$-cyclic covers in characteristic 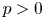$p > 0$.

Keywords

Fano varietieshypersurfacesbirational automorphismsrigidity

MSC classification

Primary: 14E07: Birational automorphisms, Cremona group and generalizations
Secondary: 14E05: Rational and birational maps 14M20: Rational and unirational varieties
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 11 , November 2022 , pp. 2033 - 2045
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author's research was partially supported by an NSF postdoctoral fellowship, DMS-2103099. The second author's research is partially supported by the NSF FRG grant number 1952399.

References

Cheltsov, I., On a smooth four-dimensional quintic, Mat. Sb. 191 (2000), 139–160.Google Scholar
Chen, N. and Stapleton, D., Fano hypersurfaces with arbitrarily large degrees of irrationality, Forum Math. Sigma 8 (2020), e24.CrossRefGoogle Scholar
Chen, N. and Stapleton, D., Rational endomorphisms of Fano hypersurfaces, Preprint (2021). arXiv:2103.12207.Google Scholar
Colliot-Thélene, J.-L. and Pirutka, A., Hypersurfaces quartiques de dimension 3: non rationalité stable, Ann. Sci. Éc. Norm. Supér. (4) 49 (2016), 371–397.CrossRefGoogle Scholar
Corti, A., Factoring birational maps of 3-folds after Sarkisov, J. Algebraic Geom. 4 (1995), 223–254.Google Scholar
de Fernex, T., Birationally rigid hypersurfaces, Invent. Math. 192 (2013), 533–566.CrossRefGoogle Scholar
de Fernex, T., Erratum to: Birationally rigid hypersurfaces, Invent. Math. 203 (2016), 675–680.CrossRefGoogle Scholar
de Fernex, T., Ein, L. and Mustaţă, M., Bounds for log canonical thresholds with applications to birational rigidity, Math. Res. Lett. 10 (2003), 219–236.Google Scholar
Fano, G., Sopra alcune varieta algebriche a tre dimensioni aventi tutti i generi nulli, Atti. Ac. Torino 43 (1908), 973–977.Google Scholar
Fano, G., Osservazioni sopra alcune varieta non razionali aventi tutti i generi nulli, Atti. Ac. Torino 50 (1915), 1067–1072.Google Scholar
Iskovskikh, V. A. and Manin, J. I., Three-dimensional quartics and counterexamples to the Lüroth problem, Mat. Sb. 86 (1971), 140–166.Google Scholar
Kollár, J., Nonrational hypersurfaces, J. Amer. Math. Soc. 8 (1995), 241–249.CrossRefGoogle Scholar
Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 32 (Springer, Berlin, 1996).CrossRefGoogle Scholar
Matsumura, H. and Monsky, P., On the automorphisms of hypersurfaces, J. Math. Kyoto Univ. 3 (1963), 347–361.Google Scholar
Poonen, B., Varieties without extra automorphisms III: hypersurfaces, Finite Fields Appl. 11 (2005), 230–268.CrossRefGoogle Scholar
Pukhlikov, A. V., Birational isomorphisms of four-dimensional quintics, Invent. Math. 87 (1987), 303–329.CrossRefGoogle Scholar
Pukhlikov, A. V., Birationally rigid Fano hypersurfaces, Izv. Math. 66 (2002), 1243.CrossRefGoogle Scholar
Pukhlikov, A. V., Birational geometry of Fano double spaces of index two, Izv. Math. 74 (2010), 925–991.CrossRefGoogle Scholar
Pukhlikov, A. V., Birational geometry of Fano hypersurfaces of index two, Math. Ann. 366 (2016), 721–782.CrossRefGoogle Scholar
Pukhlikov, A. V., Birational geometry of singular Fano hypersurfaces of index two, Manuscripta Math. 161 (2020), 161–203.CrossRefGoogle Scholar
Pukhlikov, A. V., Birational geometry of singular Fano double spaces of index two, Sb. Math. 212 (2021), 551–566.CrossRefGoogle Scholar
Schreieder, S., Stably irrational hypersurfaces of small slopes, J. Amer. Math. Soc. 32 (2019), 1171–1199.CrossRefGoogle Scholar
Totaro, B., Hypersurfaces that are not stably rational, J. Amer. Math. Soc. 29 (2016), 883–891.CrossRefGoogle Scholar
Voisin, C., Abel-Jacobi map, integral Hodge classes and decomposition of the diagonal, J. Algebraic Geom. 22 (2013), 141–174.CrossRefGoogle Scholar