Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T19:59:09.981Z Has data issue: false hasContentIssue false
  • English
  • Français

The growth of Tate–Shafarevich groups in cyclic extensions

Part of: Arithmetic algebraic geometry Algebraic number theory: global fields Abelian varieties and schemes

Published online by Cambridge University Press:  04 November 2022

Yi Ouyang  and
Jianfeng Xie
Yi Ouyang
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, China [email protected] Hefei National Laboratory, University of Science and Technology of China, Hefei 230088, China
Jianfeng Xie
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, China [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 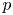$p$ be a prime number. Kęstutis Česnavičius proved that for an abelian variety 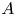$A$ over a global field 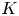$K$, the 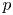$p$-Selmer group 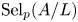$\mathrm {Sel}_{p}(A/L)$ grows unboundedly when 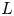$L$ ranges over the 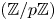$(\mathbb {Z}/p\mathbb {Z})$-extensions of 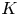$K$. Moreover, he raised a further problem: is 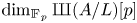$\dim _{\mathbb {F}_{p}} \text{III} (A/L) [p]$ also unbounded under the above conditions? In this paper, we give a positive answer to this problem in the case 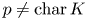$p \neq \mathrm {char}\,K$. As an application, this result enables us to generalize the work of Clark, Sharif and Creutz on the growth of potential $\text{III}$ in cyclic extensions. We also answer a problem proposed by Lim and Murty concerning the growth of the fine Tate–Shafarevich groups.

Keywords

abelian varietiesSelmer groupsTate–Shafarevich groupsfine Tate–Shafarevich groupstwist of abelian varieties

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$ 14K15: Arithmetic ground fields
Secondary: 11G05: Elliptic curves over global fields 11R34: Galois cohomology 14K05: Algebraic theory
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 10 , October 2022 , pp. 2014 - 2032
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Česnavičius, K., Selmer groups and class groups, Compos. Math. 151 (2015), 416–434.CrossRefGoogle Scholar
Česnavičius, K., Poitou-Tate without restrictions on the order, Math. Res. Lett. 22 (2015), 1621–1666.CrossRefGoogle Scholar
Česnavičius, K., Selmer groups as flat cohomology groups, J. Ramanujan Math. Soc. 31 (2016), 31–61.Google Scholar
Česnavičius, K., $p$-Selmer growth in extensions of degree $p$, J. Lond. Math. Soc. (2) 95 (2017), 833–852.CrossRefGoogle Scholar
Clark, P. L. and Sharif, S., Period, index and potential $\text{III}$, Algebra Number Theory 4 (2010), 151–174.CrossRefGoogle Scholar
Creutz, B., Potential Sha for abelian varieties, J. Number Theory 131 (2011), 2162–2174.CrossRefGoogle Scholar
Kundu, D., Growth of $p$-fine Selmer groups and $p$-fine Shafarevich-Tate groups in $\mathbb {Z}/p\mathbb {Z}$-extension, J. Ramanujan Math. Soc. 1 (2021), 1–9.Google Scholar
Lim, M. F. and Murty, V. K., The growth of fine Selmer groups, J. Ramanujan Math. Soc. 31 (2016), 79–94.Google Scholar
Madan, M. L., Class groups of global fields, J. Reine Angew. Math. 252 (1972), 171–177.Google Scholar
Matsuno, K., Elliptic curves with large Tate-Shafarevich groups over a number field, Math. Res. Lett. 16 (2009), 449–461.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Finding large Selmer rank via an arithmetic theory of local constants, Ann. of Math. (2) 166 (2007), 579–612.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Diophantine stability, with an appendix by M. Larsen, Amer. J. Math. 140 (2018), 571–616.Google Scholar
Mazur, B., Rubin, K. and Silverberg, A., Twisting commutative algebraic groups, J. Algebra 314 (2007), 419–438.CrossRefGoogle Scholar
Milne, J. S., On the arithmetic of abelian varieties, Invent. Math. 17 (1972), 177–190.CrossRefGoogle Scholar
Neukirch, J., Algebraic number theory, Grundl. Math. Wissen., vol. 322 (Springer, 2013).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, Grundl. Math. Wissen., vol. 323, second edition (Springer, 2008).CrossRefGoogle Scholar
Wuthrich, C., The fine Tate-Shafarevich group, Math. Proc. Cambridge Philos. Soc. 142 (2007), 1–12.CrossRefGoogle Scholar