Article contents
Geometry and topology of the space of Kähler metrics on singular varieties
Published online by Cambridge University Press: 19 July 2018
Abstract
Let 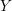 $Y$ be a compact Kähler normal space and let
$Y$ be a compact Kähler normal space and let 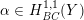 $\unicode[STIX]{x1D6FC}\in H_{\mathit{BC}}^{1,1}(Y)$ be a Kähler class. We study metric properties of the space
$\unicode[STIX]{x1D6FC}\in H_{\mathit{BC}}^{1,1}(Y)$ be a Kähler class. We study metric properties of the space 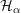 ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}$ of Kähler metrics in
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}$ of Kähler metrics in 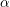 $\unicode[STIX]{x1D6FC}$ using Mabuchi geodesics. We extend several results of Calabi, Chen, and Darvas, previously established when the underlying space is smooth. As an application, we analytically characterize the existence of Kähler–Einstein metrics on
$\unicode[STIX]{x1D6FC}$ using Mabuchi geodesics. We extend several results of Calabi, Chen, and Darvas, previously established when the underlying space is smooth. As an application, we analytically characterize the existence of Kähler–Einstein metrics on 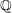 $\mathbb{Q}$-Fano varieties, generalizing a result of Tian, and illustrate these concepts in the case of toric varieties.
$\mathbb{Q}$-Fano varieties, generalizing a result of Tian, and illustrate these concepts in the case of toric varieties.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
Footnotes
Current address: IHES, Université Paris Saclay, 91400 Bures sur Yvette, France email [email protected]
References
- 11
- Cited by


