Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T04:41:09.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating functions on covering groups

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  20 February 2018

David Ginzburg
David Ginzburg*
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Ramat Aviv, Tel Aviv 6997801, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove a conjecture relating the Whittaker function of a certain generating function with the Whittaker function of the theta representation 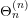$\unicode[STIX]{x1D6E9}_{n}^{(n)}$. This enables us to establish that a certain global integral is factorizable and hence deduce the meromorphic continuation of the standard partial 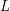$L$ function 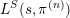$L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$. In fact we prove that this partial 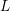$L$ function has at most a simple pole at 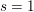$s=1$. Here, 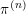$\unicode[STIX]{x1D70B}^{(n)}$ is a genuine irreducible cuspidal representation of the group 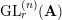$\text{GL}_{r}^{(n)}(\mathbf{A})$.

Keywords

L functionsmetaplectic covering groupsgenerating functions

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 11F55: Other groups and their modular and automorphic forms (several variables) 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 4 , April 2018 , pp. 671 - 684
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bump, D. and Friedberg, S., Metaplectic generating functions and Shimura integrals , in Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996), Proceedings of Symposia in Pure Mathematics, vol. 66, Part 2 (American Mathematical Society, Providence, RI, 1999), 1–17.Google Scholar
Bump, D. and Ginzburg, D., Symmetric square L-functions on GL(r) , Ann. of Math. (2) 136 (1992), 137–205.Google Scholar
Bump, D. and Hoffstein, J., Some Euler products associated with cubic metaplectic forms on GL(3) , Duke Math. J. 53 (1986), 1047–1072.Google Scholar
Bump, D. and Hoffstein, J., On Shimura’s correspondence , Duke Math. J. 55 (1987), 661–691.Google Scholar
Cai, Y., Fourier coefficients for theta representations on covers of general linear groups , Trans. Amer. Math. Soc. to appear, doi:10.1090/tran/7429. Preprint (2016), arXiv:1602.06614.Google Scholar
Cai, Y., Friedberg, S., Ginzburg, D. and Kaplan, E., Doubling constructions for covering groups and tensor product L-functions, Preprint (2016), arXiv:1601.08240.Google Scholar
Flicker, Y. Z., Automorphic forms on covering groups of GL(2) , Invent. Math. 57 (1980), 119–182.Google Scholar
Friedberg, S. and Ginzburg, D., Criteria for the existence of cuspidal theta representations , Res. Number Theory 2 (2016), 1–16.Google Scholar
Gelbart, S. and Piatetski-Shapiro, I. I., Distinguished representations and modular forms of half-integral weight , Invent. Math. 59 (1980), 145–188.Google Scholar
Kazhdan, D. A. and Patterson, S. J., Metaplectic forms , Publ. Math. Inst. Hautes Études Sci. 59 (1984), 35–142.Google Scholar
Patterson, S. J. and Piatetski-Shapiro, I. I., A cubic analogue of the cuspidal theta representations , J. Math. Pures Appl. (9) 63 (1984), 333–375.Google Scholar
Piatetski-Shapiro, I. and Rallis, S., A new way to get Euler products , J. Reine Angew. Math. 392 (1988), 110–124.Google Scholar