Article contents
Generalized and degenerate Whittaker models
Published online by Cambridge University Press: 06 February 2017
Abstract
We study generalized and degenerate Whittaker models for reductive groups over local fields of characteristic zero (archimedean or non-archimedean). Our main result is the construction of epimorphisms from the generalized Whittaker model corresponding to a nilpotent orbit to any degenerate Whittaker model corresponding to the same orbit, and to certain degenerate Whittaker models corresponding to bigger orbits. We also give choice-free definitions of generalized and degenerate Whittaker models. Finally, we explain how our methods imply analogous results for Whittaker–Fourier coefficients of automorphic representations. For 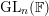 $\text{GL}_{n}(\mathbb{F})$ this implies that a smooth admissible representation
$\text{GL}_{n}(\mathbb{F})$ this implies that a smooth admissible representation  $\unicode[STIX]{x1D70B}$ has a generalized Whittaker model
$\unicode[STIX]{x1D70B}$ has a generalized Whittaker model 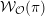 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ corresponding to a nilpotent coadjoint orbit
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ corresponding to a nilpotent coadjoint orbit 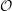 ${\mathcal{O}}$ if and only if
${\mathcal{O}}$ if and only if 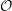 ${\mathcal{O}}$ lies in the (closure of) the wave-front set
${\mathcal{O}}$ lies in the (closure of) the wave-front set 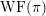 $\operatorname{WF}(\unicode[STIX]{x1D70B})$. Previously this was only known to hold for
$\operatorname{WF}(\unicode[STIX]{x1D70B})$. Previously this was only known to hold for  $\mathbb{F}$ non-archimedean and
$\mathbb{F}$ non-archimedean and 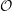 ${\mathcal{O}}$ maximal in
${\mathcal{O}}$ maximal in 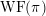 $\operatorname{WF}(\unicode[STIX]{x1D70B})$, see Moeglin and Waldspurger [Modeles de Whittaker degeneres pour des groupes p-adiques, Math. Z. 196 (1987), 427–452]. We also express
$\operatorname{WF}(\unicode[STIX]{x1D70B})$, see Moeglin and Waldspurger [Modeles de Whittaker degeneres pour des groupes p-adiques, Math. Z. 196 (1987), 427–452]. We also express 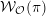 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ as an iteration of a version of the Bernstein–Zelevinsky derivatives [Bernstein and Zelevinsky, Induced representations of reductive p-adic groups. I., Ann. Sci. Éc. Norm. Supér. (4) 10 (1977), 441–472; Aizenbud et al., Derivatives for representations of
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ as an iteration of a version of the Bernstein–Zelevinsky derivatives [Bernstein and Zelevinsky, Induced representations of reductive p-adic groups. I., Ann. Sci. Éc. Norm. Supér. (4) 10 (1977), 441–472; Aizenbud et al., Derivatives for representations of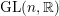 $\text{GL}(n,\mathbb{R})$and
$\text{GL}(n,\mathbb{R})$and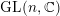 $\text{GL}(n,\mathbb{C})$, Israel J. Math. 206 (2015), 1–38]. This enables us to extend to
$\text{GL}(n,\mathbb{C})$, Israel J. Math. 206 (2015), 1–38]. This enables us to extend to 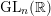 $\text{GL}_{n}(\mathbb{R})$ and
$\text{GL}_{n}(\mathbb{R})$ and  $\text{GL}_{n}(\mathbb{C})$ several further results by Moeglin and Waldspurger on the dimension of
$\text{GL}_{n}(\mathbb{C})$ several further results by Moeglin and Waldspurger on the dimension of 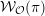 ${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ and on the exactness of the generalized Whittaker functor.
${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ and on the exactness of the generalized Whittaker functor.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 31
- Cited by


