Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T05:26:48.247Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact functors on perverse coherent sheaves

Part of: Local theory Abelian categories (Co)homology theory

Published online by Cambridge University Press:  04 May 2015

Clemens Koppensteiner
Clemens Koppensteiner*
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Rd, Evanston, IL 60208, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Inspired by symplectic geometry and a microlocal characterizations of perverse (constructible) sheaves we consider an alternative definition of perverse coherent sheaves. We show that a coherent sheaf is perverse if and only if 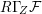$R{\rm\Gamma}_{Z}{\mathcal{F}}$ is concentrated in degree 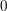$0$ for special subvarieties 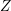$Z$ of 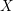$X$. These subvarieties 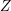$Z$ are analogs of Lagrangians in the symplectic case.

Keywords

perverse coherent sheaveslocal cohomology

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions
Secondary: 18E30: Derived categories, triangulated categories 14B15: Local cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 9 , September 2015 , pp. 1688 - 1696
Copyright
© The Author 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arinkin, D. and Bezrukavnikov, R., Perverse coherent sheaves, Mosc. Math. J. 10 (2010), 3–29.CrossRefGoogle Scholar
Beauville, A., Symplectic singularities, Invent. Math. 139 (2000), 541–549.CrossRefGoogle Scholar
Bezrukavnikov, R., Perverse coherent sheaves (after Deligne), Preprint (2000), arXiv:math/0005152.Google Scholar
Brodmann, M. P. and Sharp, R. Y., Local cohomology: an algebraic introduction with geometric applications, Cambridge Studies in Advanced Mathematics, vol. 60 (Cambridge University Press, Cambridge, 1998), doi:10.1017/CBO9780511629204.Google Scholar
Hartshorne, R., Residues and duality, Lecture Notes in Mathematics, vol. 20 (Springer, Berlin, 1966).Google Scholar
Kashiwara, M., t-structures on the derived categories of holonomic D-modules and coherent 𝓞-modules, Mosc. Math. J. 4 (2004), 847–868.CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds, Grundlehren der Mathematischen Wissenschaften, vol. 292 (Springer, Berlin, 1994).Google Scholar
Mirkovi, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143; doi:10.4007/annals.2007.166.95.CrossRefGoogle Scholar
Grothendieck, A. and Raynaud, M., Cohomologie locale des faisceaux co-hérents et théorémes de Lefschetz locaux et globaux (SGA2), Documents Mathématiques, vol. 4 (Société Mathématique de France, Paris, 2005); arXiv:math/0511279; MR 2171939.Google Scholar
Williamson, G., Vanishing of !-restriction of constructible sheaves, MathOverflow (2013), http://mathoverflow.net/a/129244.Google Scholar