Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T04:15:13.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of irreversible and reversible Pimsner operator algebras

Part of: Linear spaces and algebras of operators Selfadjoint operator algebras

Published online by Cambridge University Press:  13 January 2021

Adam Dor-On ,
Søren Eilers  and
Shirly Geffen
Adam Dor-On
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetspark 5, 2100Copenhagen, [email protected]
Søren Eilers
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetspark 5, 2100Copenhagen, [email protected]
Shirly Geffen
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, PO box 653, Be'er Sheva, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Since their inception in the 1930s by von Neumann, operator algebras have been used to shed light on many mathematical theories. Classification results for self-adjoint and non-self-adjoint operator algebras manifest this approach, but a clear connection between the two has been sought since their emergence in the late 1960s. We connect these seemingly separate types of results by uncovering a hierarchy of classification for non-self-adjoint operator algebras and 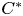$C^{*}$-algebras with additional 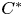$C^{*}$-algebraic structure. Our approach naturally applies to algebras arising from 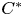$C^{*}$-correspondences to resolve self-adjoint and non-self-adjoint isomorphism problems in the literature. We apply our strategy to completely elucidate this newly found hierarchy for operator algebras arising from directed graphs.

Keywords

classificationtensor algebrasPimsner algebrasrigiditynon-commutative boundaryK-theorygraph algebrasreconstruction

MSC classification

Primary: 47L30: Abstract operator algebras on Hilbert spaces 46L35: Classifications of $C^*$-algebras
Secondary: 47L55: Representations of (nonselfadjoint) operator algebras 46L80: $K$-theory and operator algebras (including cyclic theory) 46L08: $C^*$-modules
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2510 - 2535
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by NSF grant DMS-1900916 and by the European Union's Horizon 2020 Marie Sklodowska-Curie grant No 839412. The second author was supported by the DFF-Research Project 2 ‘Automorphisms and Invariants of Operator Algebras’, no. 7014-00145B, and by the DNRF through the Centre for Symmetry and Deformation (DNRF92). The third author was supported by a Negev fellowship, a Minerva fellowship programme, an ISF grant no. 476/16 and the DFG through SFB 878 and EXC 2044 Mathematics Münster: Dynamics–Geometry–Structure.

References

Arveson, W. B., Operator algebras and measure preserving automorphisms, Acta Math. 118 (1967), 95–109.CrossRefGoogle Scholar
Arveson, W. B., Subalgebras of $C^{\ast }$-algebras, Acta Math. 123 (1969), 141–224.CrossRefGoogle Scholar
Arveson, W. B., Subalgebras of $C^{\ast }$-algebras. II, Acta Math. 128 (1972), 271–308.CrossRefGoogle Scholar
Arveson, W. B., Subalgebras of $C^{\ast }$-algebras. III. Multivariable operator theory, Acta Math. 181 (1998), 159–228.CrossRefGoogle Scholar
Asadi, M. B., Hilbert $C^{*}$-modules and $*$-isomorphisms, J. Operator Theory 59 (2008), 431–434.Google Scholar
Blecher, D. P. and Le Merdy, C., Operator algebras and their modules—an operator space approach, London Mathematical Society Monographs, New Series, vol. 30 (The Clarendon Press, Oxford, 2004).CrossRefGoogle Scholar
Brown, L. G., Green, P. and Rieffel, M. A., Stable isomorphism and strong Morita equivalence of $C^{*}$-algebras, Pacific J. Math. 71 (1977), 349–363.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., $C^{*}$-algebras and finite-dimensional approximations, Graduate Studies in Mathematics, vol. 88 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Brownlowe, N., Laca, M., Robertson, D. and Sims, A., Reconstructing directed graphs from generalised gauge actions on their Toeplitz algebras, Proc. Roy. Soc. Edinburgh Sect. A, 150 (2020), 2632–2641.CrossRefGoogle Scholar
Carlsen, T. M., Ruiz, E., Sims, A. and Tomforde, M., Reconstruction of groupoids and $C^{*}$-rigidity of dynamical systems, to appear. Preprint (2017), arXiv:1711.01052.Google Scholar
Choquet, G. and Meyer, P.-A., Existence et unicité des représentations intégrales dans les convexes compacts quelconques, Ann. Inst. Fourier (Grenoble) 13 (1963), 139–154.CrossRefGoogle Scholar
Cuntz, J. and Krieger, W., A class of $C^{*}$-algebras and topological Markov chains, Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
Davidson, K. R. and Katsoulis, E. G., Isomorphisms between topological conjugacy algebras, J. Reine Angew. Math. 621 (2008), 29–51.Google Scholar
Davidson, K. R. and Katsoulis, E. G., Operator algebras for multivariable dynamics, Mem. Amer. Math. Soc. 209 (2011), 53.Google Scholar
Davidson, K. R. and Katsoulis, E. G., Dilation theory, commutant lifting and semicrossed products, Doc. Math. 16 (2011), 781–868.Google Scholar
Davidson, K. R., Ramsey, C. and Shalit, O. M., The isomorphism problem for some universal operator algebras, Adv. Math. 228 (2011), 167–218.CrossRefGoogle Scholar
Dor-On, A., Isomorphisms of tensor algebras arising from weighted partial systems, Trans. Amer. Math. Soc. 370 (2018), 3507–3549.CrossRefGoogle Scholar
Dor-On, A. and Katsoulis, E., Tensor algebras of product systems and their $C^{*}$-envelopes, J. Funct. Anal. 278 (2020), 108416.CrossRefGoogle Scholar
Dor-On, A. and Markiewicz, D., Operator algebras and subproduct systems arising from stochastic matrices, J. Funct. Anal. 267 (2014), 1057–1120.CrossRefGoogle Scholar
Dor-On, A. and Salomon, G., Full Cuntz–Krieger dilations via non-commutative boundaries, J. Lond. Math. Soc. 98 (2018), 416–438.CrossRefGoogle Scholar
Drinen, D. and Tomforde, M., Computing the $K$-theory and $Ext$ for graph $C^{*}$-algebra, Illinois J. Math. 46 (2002), 81–91.CrossRefGoogle Scholar
Dritschel, M. and McCullough, S., Boundary representations for families of representations of operator algebras and spaces, J. Operator Theory 53 (2005), 159–167.Google Scholar
Eilers, S., Ruiz, E. and Sørensen, A. P. W., Amplified graph $C^{*}$-algebras, Münster J. Math. 5 (2012), 121–150.Google Scholar
Exel, R., Partial dynamical systems, fell bundles and applications, Mathematical Surveys and Monographs, vol. 224 (American Mathematical Society, 2017), 321.CrossRefGoogle Scholar
Gardner, L. T., On isomorphisms of $C^{*}$-algebras, Amer. J. Math. 87 (1965), 384–396.CrossRefGoogle Scholar
Giordano, T., Matui, H., Putnam, I. F. and Skau, C. F., Orbit equivalence for Cantor minimal $\mathbb {Z}^{d}$-systems, Invent. Math. 179 (2010), 119–158.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C. F., Topological orbit equivalence and $C^{*}$-crossed products, J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Hamana, M., Injective envelopes of operator systems, Publ. Res. Inst. Math. Sci. 15 (1979), 773–785.CrossRefGoogle Scholar
Katsoulis, E., $C^{*}$-envelopes and the Hao–Ng Isomorphism for discrete groups, Int. Math. Res. Not. (IMRN) 2017 (2017), 5751–5768.Google Scholar
Katsoulis, E. and Kribs, D. W., Isomorphisms of algebras associated with directed graphs, Math. Ann. 330 (2004), 709–728.CrossRefGoogle Scholar
Katsoulis, E. and Kribs, D. W., Tensor algebras of ${C^{*}}$-correspondences and their ${C^{*}}$-envelopes, J. Funct. Anal. 234 (2006), 226–233.CrossRefGoogle Scholar
Katsura, T., A class of ${C^{*}}$-algebras generalizing both graph algebras and homeomorphism ${C^{*}}$-algebras. I. Fundamental results, Trans. Amer. Math. Soc. 356 (2004), 4287–4322 (electronic).CrossRefGoogle Scholar
Katsura, T., On ${C^{*}}$-algebras associated with ${C^{*}}$-correspondences, J. Funct. Anal. 217 (2004), 366–401; MR 2102572.CrossRefGoogle Scholar
Katsura, T., Ideal structure of $C^{*}$-algebras associated with ${C^{*}}$-correspondences, Pacific J. Math. 230 (2007), 107–145.CrossRefGoogle Scholar
Krieger, W., On ergodic flows and the isomorphism of factors, Math. Ann. 223 (1976), 19–70.CrossRefGoogle Scholar
Lance, E. C., Hilbert ${C^{*}}$-modules. A toolkit for operator algebraists, London Mathematical Society Lecture Note Series, vol. 210 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Li, X., K-theoretic invariants of semigroup $C^{*}$-algebras attached to number fields, Adv. Math. 264 (2014), 371–395.CrossRefGoogle Scholar
Li, X., K-theoretic invariants of semigroup $C^{*}$-algebras attached to number fields, Part II, Adv. Math. 291 (2016), 1–11.CrossRefGoogle Scholar
Manuilov, V. M. and Troitsky, E. V., Hilbert $C^{*}$-modules, Translations of Mathematical Monographs, vol. 226 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Meyer, R., Adjoining a unit to an operator algebra, J. Operator Theory 46 (2001), 281–288.Google Scholar
Muhly, P. and Solel, B., Tensor algebras over ${C^{*}}$-correspondences: representations, dilations and ${C^{*}}$-envelopes, J. Funct. Anal. 158 (1998), 389–457.CrossRefGoogle Scholar
Muhly, P. and Solel, B., On the Morita equivalence of tensor algebras, Proc. Lond. Math. Soc. (3) 81 (2000), 113–168.CrossRefGoogle Scholar
Paulsen, V., Completely bounded maps and operator algebras, Cambridge Studies in Advanced Mathematics, vol. 78 (Cambridge University Press, 2002); MR 1976867.Google Scholar
Pimsner, M. V., A class of $C^{*}$-algebras generalizing both Cuntz–Krieger algebras and crossed products by $\textbf {Z}$. Free probability theory (Waterloo, ON, 1995), Fields Institute Communications, vol. 12 (American Mathematical Society, Providence, RI, 1995), 189–212.Google Scholar
Raeburn, I., Graph algebras, CBMS Regional Conference Series in Mathematics, vol. 103 (American Mathematical Society, Providence, RI, 2005).CrossRefGoogle Scholar
Raeburn, I., On graded $C^{*}$-algebras, Bull. Aust. Math. Soc. 97 (2018), 127–132.CrossRefGoogle Scholar
Renault, J., Cartan subalgebras in $C^{*}$-algebras, Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
Rørdam, M., Classification of Cuntz–Krieger algebras, $K$-Theory 9 (1995), 31–58.Google Scholar
Rørdam, M., An introduction to K-theory for $C^{*}$-algebras, London Mathematical Society Student Texts, vol. 49 (Cambridge University Press, Cambridge, 2000).Google Scholar
Solel, B., You can see the arrows in a quiver operator algebra, J. Aust. Math. Soc. 77 (2004), 111–122.CrossRefGoogle Scholar
Tikuisis, A., White, S. and Winter, W., Quasidiagonality of nuclear $C^{\ast }$-algebras, Ann. of Math. (2) 185 (2017), 229–284.CrossRefGoogle Scholar