Article contents
Burgess-like subconvexity for 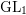 $\text{GL}_{1}$
$\text{GL}_{1}$
Published online by Cambridge University Press: 04 July 2019
Abstract
We generalize our previous method on the subconvexity problem for 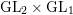 $\text{GL}_{2}\times \text{GL}_{1}$ with cuspidal representations to Eisenstein series, and deduce a Burgess-like subconvex bound for Hecke characters, that is, the bound
$\text{GL}_{2}\times \text{GL}_{1}$ with cuspidal representations to Eisenstein series, and deduce a Burgess-like subconvex bound for Hecke characters, that is, the bound 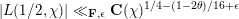 $|L(1/2,\unicode[STIX]{x1D712})|\ll _{\mathbf{F},\unicode[STIX]{x1D716}}\mathbf{C}(\unicode[STIX]{x1D712})^{1/4-(1-2\unicode[STIX]{x1D703})/16+\unicode[STIX]{x1D716}}$ for varying Hecke characters
$|L(1/2,\unicode[STIX]{x1D712})|\ll _{\mathbf{F},\unicode[STIX]{x1D716}}\mathbf{C}(\unicode[STIX]{x1D712})^{1/4-(1-2\unicode[STIX]{x1D703})/16+\unicode[STIX]{x1D716}}$ for varying Hecke characters 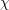 $\unicode[STIX]{x1D712}$ over a number field
$\unicode[STIX]{x1D712}$ over a number field 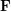 $\mathbf{F}$ with analytic conductor
$\mathbf{F}$ with analytic conductor 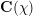 $\mathbf{C}(\unicode[STIX]{x1D712})$. As a main tool, we apply the extended theory of regularized integrals due to Zagier developed in a previous paper to obtain the relevant triple product formulas of Eisenstein series.
$\mathbf{C}(\unicode[STIX]{x1D712})$. As a main tool, we apply the extended theory of regularized integrals due to Zagier developed in a previous paper to obtain the relevant triple product formulas of Eisenstein series.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2019
Footnotes
Research partially supported by SNF-grant 200021-125291 and DFG-SNF-grant 00021L_153647.
References
- 9
- Cited by


