Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T04:49:48.722Z Has data issue: false hasContentIssue false
  • English
  • Français

The bounded height conjecture for semiabelian varieties

Part of: Abelian varieties and schemes Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  30 June 2020

Lars Kühne
Lars Kühne*
Affiliation:
Departement Mathematik und Informatik, Universität Basel, Spiegelgasse 1, 4051 Basel, Switzerland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The bounded height conjecture of Bombieri, Masser, and Zannier states that for any sufficiently generic algebraic subvariety of a semiabelian 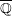$\overline{\mathbb{Q}}$-variety 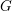$G$ there is an upper bound on the Weil height of the points contained in its intersection with the union of all algebraic subgroups having (at most) complementary dimension in 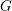$G$. This conjecture has been shown by Habegger in the case where 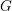$G$ is either a multiplicative torus or an abelian variety. However, there are new obstructions to his approach if 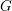$G$ is a general semiabelian variety. In particular, the lack of Poincaré reducibility means that quotients of a given semiabelian variety are intricate to describe. To overcome this, we study directly certain families of line bundles on 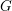$G$. This allows us to demonstrate the conjecture for general semiabelian varieties.

MSC classification

Primary: 11G50: Heights
Secondary: 14K15: Arithmetic ground fields 14G40: Arithmetic varieties and schemes; Arakelov theory; heights
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 7 , July 2020 , pp. 1405 - 1456
Copyright
© The Author 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by an Ambizione Grant of the Swiss National Science Foundation.

References

Ax, J., Some topics in differential algebraic geometry. I. Analytic subgroups of algebraic groups, Amer. J. Math. 94 (1972), 1195–1204.CrossRefGoogle Scholar
Bertrand, D., Endomorphismes de groupes algébriques; applications arithmétiques, in Diophantine approximations and transcendental numbers (Luminy, 1982), Progress in Mathematics, vol. 31 (Birkhäuser, Boston, MA, 1983), 1–45.Google Scholar
Birkenhake, C. and Lange, H., Complex abelian varieties, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 302, second edition (Springer, Berlin, 2004).CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine geometry, New Mathematical Monographs, vol. 4 (Cambridge University Press, Cambridge, 2006).Google Scholar
Bombieri, E., Masser, D. and Zannier, U., Intersecting a curve with algebraic subgroups of multiplicative groups, Int. Math. Res. Not. IMRN 1999 (1999), 1119–1140.CrossRefGoogle Scholar
Bombieri, E., Masser, D. and Zannier, U., Anomalous subvarieties – structure theorems and applications, Int. Math. Res. Not. IMRN 2007 (2007), Art. ID rnm057.10.1093/imrn/rnm057CrossRefGoogle Scholar
Bombieri, E., Masser, D. and Zannier, U., Intersecting a plane with algebraic subgroups of multiplicative groups, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 7 (2008), 51–80.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Brion, M., Algebraic groups: structure and actions, Proceedings of Symposia in Pure Mathematics, vol. 94 (American Mathematical Society, Providence, RI, 2017), 53–125.CrossRefGoogle Scholar
Chambert-Loir, A., Géométrie d’Arakelov et hauteurs canoniques sur des variétés semi-abéliennes, Math. Ann. 314 (1999), 381–401.CrossRefGoogle Scholar
Chambert-Loir, A., Points de petite hauteur sur les variétés semi-abéliennes, Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 789–821.10.1016/S0012-9593(00)01053-3CrossRefGoogle Scholar
Chambert-Loir, A. and Chambert-Loir, A., Relations de dépendance et intersections exceptionnelles (Exp. No. 1032), in Séminaire Bourbaki: Vol. 2010/2011. Exposés 1027–1042 (Société Mathématique de France, Paris, 2012), 149–188.Google Scholar
Conrad, B., A modern proof of Chevalley’s theorem on algebraic groups, J. Ramanujan Math. Soc. 17 (2002), 1–18.Google Scholar
Demailly, J.-P., Complex analytic and differential geometry. Available from http://www-fourier.ujf-grenoble.fr/∼demailly/, 09 2012.Google Scholar
Dolgachev, I. V., A modern view, in Classical algebraic geometry (Cambridge University Press, Cambridge, 2012).CrossRefGoogle Scholar
Faltings, G. and Wüstholz, G., Einbettungen kommutativer algebraischer Gruppen und einige ihrer Eigenschasten, J. Reine Angew. Math. 354 (1984), 175–205.Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 2, second edition (Springer, Berlin, 1998).CrossRefGoogle Scholar
H. Grauert, T. Peternell and R. Remmert (eds), Sheaf-theoretical methods in complex analysis, in Several complex variables. VII, Encyclopaedia of Mathematical Sciences, vol. 74 (Springer, Berlin, 1994). A reprint of Current problems in mathematics, Fundamental Directions, Vol. 74 (Russian), Vseross. Inst. Nauchn. i Tekhn. Inform. (VINITI, Moscow).CrossRefGoogle Scholar
Griffiths, P. and Harris, J., Principles of algebraic geometry, Wiley Classics Library (John Wiley & Sons, Inc., New York, 1994). Reprint of the 1978 original.CrossRefGoogle Scholar
Gunning, R. C., Function theory, in Introduction to holomorphic functions of several variables. Vol. I, The Wadsworth & Brooks/Cole Mathematics Series (Wadsworth & Brooks/Cole Advanced Books & Sostware, Pacific Grove, CA, 1990).Google Scholar
Gunning, R. C., Local theory, in Introduction to holomorphic functions of several variables. Vol. II, The Wadsworth & Brooks/Cole Mathematics Series (Wadsworth & Brooks/Cole Advanced Books & Software, Monterey, CA, 1990).Google Scholar
Habegger, P., Intersecting subvarieties of abelian varieties with algebraic subgroups of complementary dimension, Invent. Math. 176 (2009), 405–447.10.1007/s00222-008-0170-6CrossRefGoogle Scholar
Habegger, P., On the bounded height conjecture, Int. Math. Res. Not. IMRN 2009 (2009), 860–886.Google Scholar
Helgason, S., Differential geometry, Lie groups, and symmetric spaces, Graduate Studies in Mathematics, vol. 34 (American Mathematical Society, Providence, RI, 2001). Corrected reprint of the 1978 original.CrossRefGoogle Scholar
Hindry, M., Autour d’une conjecture de Serge Lang, Invent. Math. 94 (1988), 575–603.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H., An introduction, in Diophantine geometry, Graduate Texts in Mathematics, vol. 201 (Springer, New York, 2000).CrossRefGoogle Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. I, II, Ann. of Math. (2) 79 (1964), 109–203; ibid. (2) 79 (1964), 205–326.CrossRefGoogle Scholar
Huybrechts, D., An introduction, in Complex geometry, Universitext (Springer, Berlin, 2005).Google Scholar
Kirby, J., The theory of the exponential differential equations of semiabelian varieties, Selecta Math. (N.S.) 15 (2009), 445–486.CrossRefGoogle Scholar
Kleiman, S. L., Toward a numerical theory of ampleness, Ann. of Math. (2) 84 (1966), 293–344.CrossRefGoogle Scholar
Knop, F. and Lange, H., Commutative algebraic groups and intersections of quadrics, Math. Ann. 267 (1984), 555–571.CrossRefGoogle Scholar
Knop, F. and Lange, H., Some remarks on compactifications of commutative algebraic groups, Comment. Math. Helv. 60 (1985), 497–507.CrossRefGoogle Scholar
Kollár, J., Lectures on resolution of singularities, Annals of Mathematics Studies, vol. 166 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Kollár, J., Smith, K. E. and Corti, A., Rational and nearly rational varieties, Cambridge Studies in Advanced Mathematics, vol. 92 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Kühne, L., The bounded height conjecture for semiabelian varieties, Oberwolfach Rep. 13 (2016), 1060–1062.Google Scholar
Lang, S., Fundamentals of Diophantine geometry (Springer, New York, 1983).CrossRefGoogle Scholar
Lang, S., Introduction to Arakelov theory (Springer, New York, 1988).CrossRefGoogle Scholar
Laurent, M., Équations diophantiennes exponentielles, Invent. Math. 78 (1984), 299–327.CrossRefGoogle Scholar
Lazarsfeld, R., Classical setting: line bundles and linear series, in Positivity in algebraic geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 48 (Springer, Berlin, 2004).Google Scholar
Lelong, P., Intégration sur un ensemble analytique complexe, Bull. Soc. Math. France 85 (1957), 239–262.CrossRefGoogle Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, vol. 6 (Oxford University Press, Oxford, 2002). Translated from the French by Reinie Erné, Oxford Science Publications.Google Scholar
Maurin, G., Courbes algébriques et équations multiplicatives, Math. Ann. 341 (2008), 789–824.10.1007/s00208-008-0212-9CrossRefGoogle Scholar
Maurin, G., Équations multiplicatives sur les sous-variétés des tores, Int. Math. Res. Not. IMRN 2011 (2011), 5259–5366.Google Scholar
Mordell, L. J., Diophantine equations, Pure and Applied Mathematics, vol. 30 (Academic Press, London, New York, 1969).Google Scholar
Moret-Bailly, L., Familles de courbes et de variétés abéliennes sur ℙ1 . I, in Séminaire sur les Pinceaux de Courbes de Genre au Moins Deux, Astérisque, vol. 86, ed. Szpiro, L. (Société Mathématique de France, Paris, 1981).Google Scholar
Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, No. 5 (Tata Institute of Fundamental Research, Bombay, 1970).Google Scholar
Mumford, D., Varieties defined by quadratic equations, in Questions on algebraic varieties (CIME, III Ciclo, Varenna, 1969) (Edizioni Cremonese, Rome, 1970), 29–100.Google Scholar
Mumford, D., Fogarty, J. and Kirwan, F., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34, third edition (Springer, Berlin, 1994).CrossRefGoogle Scholar
Oort, F., Commutative group schemes, Lecture Notes in Mathematics, vol. 15 (Springer, Berlin, New York, 1966).CrossRefGoogle Scholar
Pink, R., A common generalization of the conjectures of André–Oort, Manin–Mumford, and Mordell–Lang. Preprint (2005), http://www.math.ethz.ch/∼pink.Google Scholar
Raynaud, M., Courbes sur une variété abélienne et points de torsion, Invent. Math. 71 (1983), 207–233.CrossRefGoogle Scholar
Raynaud, M., Sous-variétés d’une variété abélienne et points de torsion, in Arithmetic and geometry, Vol. I, Progress in Mathematics, vol. 35 (Birkhäuser Boston, Boston, MA, 1983), 327–352.CrossRefGoogle Scholar
Rémond, G., Approximation diophantienne sur les variétés semi-abéliennes, Ann. Sci. Éc. Norm. Supér. (4) 36 (2003), 191–212.CrossRefGoogle Scholar
Rémond, G., Intersection de sous-groupes et de sous-variétés. III, Comment. Math. Helv. 84 (2009), 835–863.10.4171/CMH/183CrossRefGoogle Scholar
Rudin, W., Functional analysis, International Series in Pure and Applied Mathematics, second edition (McGraw-Hill, New York, 1991).Google Scholar
Serre, J.-P., Algebraic groups and class fields, Graduate Texts in Mathematics, vol. 117 (Springer, New York, 1988). Translated from the French.10.1007/978-1-4612-1035-1CrossRefGoogle Scholar
Serre, J.-P., Espaces fibrés algébriques, in Exposés de séminaires (1950–1999), Documents Mathématiques (Paris) [Mathematical Documents (Paris)], vol. 1 (Société Mathématique de France, Paris, 2001).Google Scholar
P. Gille and P. Polo (eds), Schémas en groupes (SGA 3). Tome I. Propriétés générales des schémas en groupes, Documents Mathématiques (Paris) [Mathematical Documents (Paris)], vol. 7 (Société Mathématique de France, Paris, 2011). Séminaire de Géométrie Algébrique du Bois Marie 1962–64. [Algebraic Geometry Seminar of Bois Marie 1962–64], A seminar directed by M. Demazure and A. Grothendieck with the collaboration of M. Artin, J.-E. Bertin, P. Gabriel, M. Raynaud and J.-P. Serre, Revised and annotated edition of the 1970 French original.Google Scholar
Siu, Y. T., An effective Matsusaka big theorem, Ann. Inst. Fourier (Grenoble) 43 (1993), 1387–1405.CrossRefGoogle Scholar
Viada, E., The intersection of a curve with algebraic subgroups in a product of elliptic curves, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 2 (2003), 47–75.Google Scholar
Villareal, O. G., Moving subvarieties by endomorphisms, Manuscripta Math. 125 (2008), 81–93.CrossRefGoogle Scholar
Voisin, C., Hodge theory and complex algebraic geometry. I, Cambridge studies in Advanced Mathematics, vol. 76, English edition (Cambridge University Press, Cambridge, 2007). Translated from the French by Leila Schneps.Google Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties. I, Invent. Math. 126 (1996), 133–181.CrossRefGoogle Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties. II, Amer. J. Math. 121 (1999), 283–313.CrossRefGoogle Scholar
Waldschmidt, M., Nombres transcendants et groupes algébriques, Astérisque, vol. 69 (Société Mathématique de France, Paris, 1979). With appendices by Daniel Bertrand and Jean-Pierre Serre, with an English summary.Google Scholar
Warner, F. W., Foundations of differentiable manifolds and Lie groups, Graduate Texts in Mathematics, vol. 94 (Springer, New York, Berlin, 1983). Corrected reprint of the 1971 edition.CrossRefGoogle Scholar
Zannier, U., Polynomials with special regard to reducibility, Encyclopedia of Mathematics and its Applications, vol. 77 (Cambridge University Press, Cambridge, 2000), 517–539. Chapter Appendix by Umberto Zannier. Proof of Conjecture 1.Google Scholar
Zannier, U., Some problems of unlikely intersections in arithmetic and geometry, Annals of Mathematics Studies, vol. 181 (Princeton University Press, Princeton, NJ, 2012). With appendixes by David Masser.Google Scholar
Zilber, B., Exponential sums equations and the Schanuel conjecture, J. Lond. Math. Soc. (2) 65 (2002), 27–44.CrossRefGoogle Scholar