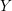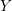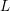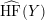Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baker, Kenneth
2020.
The Poincaré homology sphere, lens space surgeries, and some knots with tunnel number two.
Pacific Journal of Mathematics,
Vol. 305,
Issue. 1,
p.
1.
Eftekhary, Eaman
2020.
Correction to the article Floer homology and splicing knot complements.
Algebraic & Geometric Topology,
Vol. 20,
Issue. 6,
p.
3205.
Daemi, Aliakbar
Lidman, Tye
Vela-Vick, David Shea
and
Wong, C.-M. Michael
2022.
Ribbon homology cobordisms.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108580.
Hom, Jennifer
Levine, Adam Simon
and
Lidman, Tye
2022.
Knot concordance in homology cobordisms.
Duke Mathematical Journal,
Vol. 171,
Issue. 15,
Lidman, Tye
Pinzón‐Caicedo, Juanita
and
Zentner, Raphael
2023.
Toroidal integer homology three‐spheres have irreducible SU(2)$SU(2)$‐representations.
Journal of Topology,
Vol. 16,
Issue. 1,
p.
344.
Hanselman, Jonathan
Rasmussen, Jacob
and
Watson, Liam
2023.
Bordered Floer homology for manifolds with torus boundary via immersed curves.
Journal of the American Mathematical Society,
Bagherifard, Neda
and
Eftekhary, Eaman
2024.
Simple balanced three-manifolds, Heegaard
Floer homology and the Andrews–Curtis conjecture.
Algebraic & Geometric Topology,
Vol. 24,
Issue. 8,
p.
4519.
Boyer, Steven
Gordon, Cameron McA.
and
Hu, Ying
2024.
Recalibrating R$\mathbb {R}$‐order trees and Homeo+(S1)$\mbox{Homeo}_+(S^1)$‐representations of link groups.
Journal of Topology,
Vol. 17,
Issue. 4,