Article contents
Autoequivalences of twisted K3 surfaces
Published online by Cambridge University Press: 30 April 2019
Abstract
Derived equivalences of twisted K3 surfaces induce twisted Hodge isometries between them; that is, isomorphisms of their cohomologies which respect certain natural lattice structures and Hodge structures. We prove a criterion for when a given Hodge isometry arises in this way. In particular, we describe the image of the representation which associates to any autoequivalence of a twisted K3 surface its realization in cohomology: this image is a subgroup of index 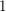 $1$ or
$1$ or 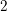 $2$ in the group of all Hodge isometries of the twisted K3 surface. We show that both indices can occur.
$2$ in the group of all Hodge isometries of the twisted K3 surface. We show that both indices can occur.
- Type
- Research Article
- Information
- Copyright
- © The Author 2019
Footnotes
This material is based upon work supported by the National Science Foundation under grant no. DMS-1501461 and by the Studienstiftung des deutschen Volkes.
References
- 5
- Cited by


