Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T04:25:13.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetic purity of strong approximation for semi-simple simply connected groups

Part of: Multiplicative number theory Linear algebraic groups and related topics Arithmetic algebraic geometry

Published online by Cambridge University Press:  01 February 2021

Yang Cao  and
Zhizhong Huang
Yang Cao
Affiliation:
University of Science and Technology of China, School of Mathematical Sciences, 96 Jinzhai Road, 230026Hefei, Anhui, [email protected]
Zhizhong Huang
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, 53111Bonn, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we establish the arithmetic purity of strong approximation for certain semisimple simply connected linear algebraic groups and their homogeneous spaces over a number field 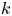$k$. For instance, for any such group 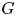$G$ and for any open subset 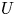$U$ of 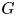$G$ with 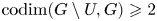${\mathrm {codim}}(G\setminus U, G)\geqslant 2$, we prove that (i) if 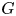$G$ is 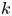$k$-simple and 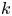$k$-isotropic, then 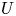$U$ satisfies strong approximation off any finite number of places; and (ii) if 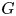$G$ is the spin group of a non-degenerate quadratic form which is not compact over archimedean places, then 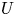$U$ satisfies strong approximation off all archimedean places. As a consequence, we prove that the same property holds for affine quadratic hypersurfaces. Our approach combines a fibration method with subgroup actions developed for induction on the codimension of 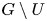$G\setminus U$, and an affine linear sieve which allows us to produce integral points with almost-prime polynomial values.

Keywords

strong approximationlinear algebraic groupsaffine linear sieves

MSC classification

Secondary: 11G35: Varieties over global fields 20G35: Linear algebraic groups over adèles and other rings and schemes 11N36: Applications of sieve methods
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2628 - 2649
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

American Institute of Mathematics, AIM open problem session 2014, http://aimath.org/pastworkshops/ratlhigherdimvarproblems.pdf.Google Scholar
Anantharaman, S., Schémas en groupes, espaces homogènes et espaces algébriques sur une base de dimension 1, Mém. Soc. Math. Fr. (N.S.) 33 (1973), 5–79.Google Scholar
Borel, A., Linear algebraic groups, second edition, Graduate Texts in Mathematics, vol. 126 (Springer, New York, NY, 1991).CrossRefGoogle Scholar
Borovoi, M., On representations of integers by indefinite ternary quadratic forms, J. Number Theory 90 (2001), 281–293.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Cao, Y., Liang, Y. and Xu, F., Arithmetic purity of strong approximation for homogeneous spaces, J. Math. Pures Appl. (9) 132 (2019), 334–368.CrossRefGoogle Scholar
Cao, Y. and Xu, F., Strong approximation with Brauer-Manin obstruction for toric varieties, Ann. Inst. Fourier (Grenoble) 68 (2018), 1879–1908.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Xu, F., Brauer-Manin obstruction for integral points of homogeneous spaces and representation of integral quadratic forms, Compos. Math. 145 (2009), 309–363.CrossRefGoogle Scholar
Conrad, B., Weil and Grothendieck approaches to adelic points, Enseign. Math. 58 (2012), 61–97.CrossRefGoogle Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive groups, second edition, New Mathematical Monographs, vol. 17 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Duke, W., Rudnick, Z. and Sarnak, P., Density of integer points on affine homogeneous varieties, Duke Math. J. 71 (1993), 143–179.CrossRefGoogle Scholar
Eichler, M., Allgemeine Kongruenzklassenteilungen der Ideal einfacher Algebren über algebraischen Zahlkörpern und ihre L-Reihen, J. Reine Angew. Math. 179 (1938), 227–251.Google Scholar
Friedlander, J. and Iwaniec, H., Opera de cribro, Colloquium Publications, vol. 57 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Gorodnik, A. and Weiss, B., Distribution of lattice orbits on homogeneous varieties, Geom. Funct. Anal. 17 (2007), 58–115.CrossRefGoogle Scholar
Grothendieck, A., Le groupe de Brauer. III. Exemples et compléments, Dix Exposés sur la Cohomologie des Schémas (North-Holland, Amsterdam, 1968), 88–188.Google Scholar
Halberstam, H. and Richert, H. E., Sieve methods, London Mathematical Society Monographs, vol. 4 (Academic Press, London, 1974).Google Scholar
Harari, D., Le défaut d'approximation forte pour les groupes algébriques commutatifs, Algebra Number Theory 2 (2008), 595–611.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, NY, 1977).CrossRefGoogle Scholar
Humphreys, J., Linear algebraic groups, Graduate Texts in Mathematics, vol. 21 (Springer, New York, NY, 1975).CrossRefGoogle Scholar
Kneser, M., Starke Approximation in algebraischen Gruppen I, J. Reine Angew. Math. 218 (1965), 190–203.Google Scholar
Maucourant, F., Homogeneous asymptotic limits of Haar measures of semisimple linear groups and their lattices, Duke Math. J. 136 (2007), 357–399.CrossRefGoogle Scholar
Minčhev, K. P., Strong approximation for varieties over an algebraic number field, Dokl. Akad. Nauk BSSR 33 (1989), 5–8.Google Scholar
Nevo, A. and Sarnak, P., Prime and almost prime integral points on principal homogeneous spaces, Acta Math. 205 (2010), 361–402.CrossRefGoogle Scholar
Platonov, V. P., The strong approximation problem and the Kneser-Tits conjecture for algebraic groups, Izv. Akad. Nauk SSSR, Ser. Mat. 33 (1969), 1211–1219.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic Press, Boston, MA, 1994).Google Scholar
Poonen, B., Rational points on varieties, Graduate Studies in Mathematics, vol. 186 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Popov, V. L. and Vinberg, E. B., Invariant theory, in Algebraic Geometry IV, eds A. N. Parshin and I. R. Shafarevich, Encyclopaedia of Mathematical Sciences, vol. 55 (Springer, Berlin, 1994).Google Scholar
Serre, J.-P., Topics in galois theory, Research Notes in Mathematics, vol. 1 (Jones and Bartlett Publishers, Boston, MA, 1992).Google Scholar
Szamuely, T., Galois groups and fundamental groups, Cambridge Studies in Advanced Mathematics, vol. 117 (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory, Cambridge Studies in Advanced Mathematics, vol. 46 (Cambridge University Press, Cambridge, 1995).Google Scholar
Wei, D., Strong approximation for a toric variety, Preprint (2014), arXiv:1403.1035.Google Scholar
Wittenberg, O., Rational points and zero-cycles on rationally connected varieties over number fields, in Algebraic Geometry: Salt Lake City 2015, Part 2, 597–635, Proceedings of Symposia in Pure Mathematics, vol. 97 (American Mathematical Society, Providence, RI, 2018).CrossRefGoogle Scholar