Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T07:55:22.675Z Has data issue: false hasContentIssue false
  • English
  • Français

A Well-Conditioned Hypersingular Boundary Element Method for Electrostatic Potentials in the Presence of Inhomogeneities within Layered Media

Part of: Higher-dimensional theory Physiological, cellular and medical topics

Published online by Cambridge University Press:  12 April 2016

Brian Zinser  and
Wei Cai
Brian Zinser
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Charlotte, Charlotte, NC 28223, USA
Wei Cai*
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Charlotte, Charlotte, NC 28223, USA INS, Shanghai Jiaotong University, Shanghai 200240, P.R. China
*
*Corresponding author. Email addresses:[email protected] (B. Zinser), [email protected] (W. Cai)
Get access

Abstract

In this paper, we will present a high-order, well-conditioned boundary element method (BEM) based on Müller's hypersingular second kind integral equation formulation to accurately compute electrostatic potentials in the presence of inhomogeneity embedded within layered media. We consider two types of inhomogeneities: the first one is a simple model of an ion channel which consists of a finite height cylindrical cavity embedded in a layered electrolytes/membrane environment, and the second one is a Janus particle made of two different semi-spherical dielectric materials. Both types of inhomogeneities have relevant applications in biology and colloidal material, respectively. The proposed BEM gives 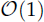condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.

Keywords

Poisson Boltzmann equationLayered electrolytes and dielectricsJanus particlesion channelsexplicit/implicit hybrid solvation model

MSC classification

Secondary: 31B05: Harmonic, subharmonic, superharmonic functions 92C05: Biophysics 65Z05: Applications to physics
Type
Research Article
Information
Communications in Computational Physics , Volume 19 , Issue 4 , April 2016 , pp. 970 - 997
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Atkinson, K. and Graham, I.. Iterative variants of the Nystrom method for second kind boundary integral operators. SIAM J. Sci. Stat. Comput., 13:694–722,1990.Google Scholar
[2]Barros, K. and Luijten, E.. Dielectric Effects in the Self-Assembly of Binary Colloidal Aggregates. Phys. Rev. Lett., 113:017801,2014.Google Scholar
[3]Bremer, J.. On the Nystrom discretization of integral equations on planar curves with corners. Appl. Comput. Harmon. Anal., 32:45–64, 2012.Google Scholar
[4]Böttcher, C. J. F.. Theory of Electric Polarization, vol. 1: Dielectricsin Static Fields, 2nd ed. Elsevier Sciences, Amsterdam, 1973.Google Scholar
[5]Cai, W.. Computational Methods for Electromagnetic Phenomena. Cambridge Univ. Press, Cambridge, 2013.Google Scholar
[6]Cai, W., Deng, S., and Jacobs, D.. Extending the fast multipole method to charges inside or outside a dielectric sphere. J. Comput. Phys., 223:846–864,2007.Google Scholar
[7]Chandler, G.. Galerkin's method for boundary integral equations on polygonal domains. J. Aust. Math. Soc. Ser. B, Appl. Math., 26:1–13,1984.Google Scholar
[8]Chen, L., Holst, M., and Xu, J.. The finite element approximation of the nonlinear Poisson-Boltzmann equation. SIAM J. Numer. Anal., 45:2298–2320,2007.Google Scholar
[9]Chern, I.-L., Lie, J.-G., and Wang, W.-C.. Accurate evaluation of electrostatics for macromolecules in solution. Meth. Appl. Anal., 10:309–328,2003.Google Scholar
[10]Deng, S. and Cai, W.. Analysis and application of an orthogonal nodal basis on triangles for discontinuous spectral element methods. Appl. Num. Anal. Comp. Math., 2:326–345,2005.Google Scholar
[11]Dunavant, D.. High degree efficient symmetrical gaussian quadrature rules for the triangle. Int. J. Numer. Meth. Engng., 21:1129–1148,1985.Google Scholar
[12]Fogolari, F., Brigo, A., and Molinari, H.. The Poisson-Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit., 15:377–392,2002.Google Scholar
[13]Juffer, A. H., Botta, E. F. F., van Keulen, B. A. M., van der Ploeg, A., and Berendsen, H. J. C.. The electric potential of a macromolecule in a solvent: A fundamental approach. J. Comput. Phys., 97:144–171,1991.Google Scholar
[14]Kress, R. A.. A Nyström method for boundary integral equations in domains with corners. Numer. Math., 58:145–161,1990.Google Scholar
[15]Lin, H., Tang, H., and Cai, W.. Accuracy and efficiency in computing electrostatic potential for an ion channel model in layered dielectric/electrolyte media. J. Comput. Phys., 259:448–512, 2013.Google Scholar
[16]Lu, B., Cheng, X., Huang, J., and McCammon, J. A.. Order N algorithm for computation of electrostatic interactions in biomolecular systems. Proc. Natl. Acad. Sci. USA, 103:19314–19319, 2006.Google Scholar
[17]Müller, C.. Foundations of the Mathematical Theory of Electromagnetic Waves. Springer-Verlag, Berlin Heidelberg, 1969.Google Scholar
[18]Nédélec, J. C.. Acoustic and Electromagnetic Equations: Integral Representations for Harmonic Problems. Springer-Verlag New York, 2001.Google Scholar
[19]Rokhlin, V.. Solution of acoustic scattering problem by means of second kind of integral equations. Wave Motion, 5:257–272,1983.Google Scholar
[20]Still, W. C., Tempczyk, A., Hawley, R. C., and Hendrickson, T.. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc., 112:6127–6129,1990.Google Scholar
[21]Walther, A. and Müller, A. H. E., Janus particles: Synthesis, self-assembly, physical properties, and applications. Chem. Rev., 113:5194–5261,2013.Google Scholar
[22] Mathematica, Version 10.0. Wolfram Research, Inc., Champaign, IL, 2014.Google Scholar
[23]Xu, Z. L. and Cai, W.. Fast analytical methods for macroscopic electrostatic models in biomolecular simulations. SIAM Review, 53:683–720,2011.Google Scholar