Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T13:55:19.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling Regimes and the Singularity of Specific Heat in the 3D Ising Model

Published online by Cambridge University Press:  03 June 2015

J. Kaupužs ,
R. V. N. Melnik  and
J. Rimšāns
J. Kaupužs*
Affiliation:
Institute of Mathematics and Computer Science, University of Latvia, 29 Raiņa Boulevard, LV1459, Riga, Latvia Institute of Mathematical Sciences and Information Technologies, University of Liepaja, 14 Liela Street, Liepaja LV-3401, Latvia
R. V. N. Melnik*
Affiliation:
Wilfrid Laurier University, Waterloo, Ontario, Canada, N2L 3C5
J. Rimšāns*
Affiliation:
Institute of Mathematics and Computer Science, University of Latvia, 29 Raiņa Boulevard, LV1459, Riga, Latvia Institute of Mathematical Sciences and Information Technologies, University of Liepaja, 14 Liela Street, Liepaja LV-3401, Latvia
*
Corresponding author.Email:[email protected]
Email:[email protected]
Email:[email protected]
Get access

Abstract

The singularity of specific heat CV of the three-dimensional Ising model is studied based on Monte Carlo data for lattice sizes L≤1536. Fits of two data sets, one corresponding to certain value of the Binder cumulant and the other — to the maximum of CV, provide consistent values of C0 in the ansatz CV(L)=C0+ALα/ν at large L, if α/ν=0.196(6). However, a direct estimation from our 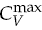data suggests that α/ν, most probably, has a smaller value (e.g., α/ν= 0.113(30)). Thus, the conventional power-law scaling ansatz can be questioned because of this inconsistency. We have found that the data are well described by certain logarithmic ansatz.

Keywords

65C0582B2082B8082B27Ising modelMonte Carlo simulationspecific heatfinite-size scalingcritical exponents
Type
Research Article
Information
Communications in Computational Physics , Volume 14 , Issue 2 , August 2013 , pp. 355 - 369
Copyright
Copyright © Global Science Press Limited 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Hasenbusch, M., Int. J. Mod. Phys. C 12 (2001) 911.Google Scholar
[2]Deng, Y., Bloöte, H. W. J., Phys. Rev. E 68 (2003) 036125.Google Scholar
[3]Chen, J.-H., Fisher, M. E., Phys. Rev. Lett. 48 (1982) 630.Google Scholar
[4]Bloöte, H. W. J., Luijten, E., Heringa, J. R., J. Phys. A: Math. Gen. 28 (1995) 6289.Google Scholar
[5]Feng, X., Bloöte, H. W. J., Phys. Rev. E 81 (2010) 031103.Google Scholar
[6]Hasenbusch, M., Phys. Rev. B 82 (2010) 174433.Google Scholar
[7]Hasenbusch, M., Phys. Rev. B 82 (2010) 174434.Google Scholar
[8]Kaupuzˇs, J., Rimsøāns, J., Melnik, R. V. N., Ukr. J. Phys. 56 (2011) 845.Google Scholar
[9]Stauffer, D., Braz. J. Phys. 30 (2000) 787.CrossRefGoogle Scholar
[10]Kaupuzˇs, J., Ann. Phys. (Berlin) 10 (2001) 299.Google Scholar
[11]Kaupuzˇs, J., Progress of Theoretical Physics 124 (2010) 613.Google Scholar
[12]Zhang, Z-D., Philosophical Magazine 87 (2007) 5309.Google Scholar
[13]Guida, R., Zinn-Justin, J., J. Phys. A 31 (1998) 8103.CrossRefGoogle Scholar
[14]Wolff, U., Phys. Rev. Lett. 62 (1989) 361.Google Scholar
[15]Kaupuzˇs, J., Rimsøāns, J., Melnik, R. V. N., Phys. Rev. E 81 (2010) 026701.Google Scholar
[16]Amit, D. J., Field Theory, the Renormalization Group, and Critical Phenomena, World Scientific, Singapore, 1984.Google Scholar
[17]Ma, S.-K., Modern Theory of Critical Phenomena, W. A. Benjamin, Inc., New York, 1976.Google Scholar
[18]Zinn-Justin, J., Quantum Field Theory and Critical Phenomena, Clarendon Press, Oxford, 1996.Google Scholar
[19]Kleinert, H., Schulte-Frohlinde, V., Critical Properties of ø 4 Theories, World Scientific, Singapore, 2001.Google Scholar
[20]Pelissetto, A., Vicari, E., Phys. Rep. 368 (2002) 549.Google Scholar
[21]Newman, K. E., Riedel, E. K., Phys. Rev. B 30 (1984) 6615.Google Scholar
[22]Tseskis, A. L., Exp, J.Theor. Phys. 75 (1992) 269.Google Scholar
[23]Janke, W., Kenna, R., Nucl. Phys. Proc. Suppl. 106 (2002) 929.Google Scholar
[24]Press, W. H., Flannery, B. P., Teukolsky, S. A., Vetterling, W. T., Numerical Recipes - The Art of Scientific Computing, Cambridge University Press, Cambridge, 1989.Google Scholar
[25]Campostrini, M., Pelissetto, A., Rossi, P., Vicari, E., Phys. Rev. E 65 (2002) 066127.Google Scholar
[26]Butera, P., Comi, M., Phys. Rev. B 65 (2002) 144431.Google Scholar
[27]Butera, P., Comi, M., Phys. Rev. B 72 (2005) 014442.Google Scholar
[28]Collura, M., J. Stat. Mech. (2010) P12036.CrossRefGoogle Scholar
[29]Kaupuzˇs, J., Can. J. Phys. 90 (2012) 373.Google Scholar
[30]Haäggkvist, R., Rosengren, A., Lundow, P. H., Markstroäm, K., Andreén, D., Kundrotas, P., Advances in Physics 56 (2007) 653.Google Scholar
[31]Lundow, P. H., Markstroäm, K., Rosengren, A., Philosophical Magazine 89 (2009) 2009.Google Scholar