Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T19:34:23.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Precorrected-FFT Accelerated Singular Boundary Method for Large-Scale Three-Dimensional Potential Problems

Part of: Numerical methods in Fourier analysis Partial differential equations, boundary value problems Partial differential equations, initial value and time-dependent initial-boundary value problems

Published online by Cambridge University Press:  21 June 2017

Weiwei Li ,
Wen Chen  and
Zhuojia Fu
Weiwei Li*
Affiliation:
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, International Center for Simulation Software in Engineering and Sciences, College of Mechanics and Materials, Hohai University, Nanjing 210098, P.R. China State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, P.R. China
Wen Chen*
Affiliation:
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, International Center for Simulation Software in Engineering and Sciences, College of Mechanics and Materials, Hohai University, Nanjing 210098, P.R. China State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, P.R. China
Zhuojia Fu*
Affiliation:
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, International Center for Simulation Software in Engineering and Sciences, College of Mechanics and Materials, Hohai University, Nanjing 210098, P.R. China State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, P.R. China
*
*Corresponding author. Email addresses:[email protected] (W. Li), [email protected] (W. Chen), [email protected] (Z. Fu)
*Corresponding author. Email addresses:[email protected] (W. Li), [email protected] (W. Chen), [email protected] (Z. Fu)
*Corresponding author. Email addresses:[email protected] (W. Li), [email protected] (W. Chen), [email protected] (Z. Fu)
Get access

Abstract

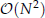This study makes the first attempt to accelerate the singular boundary method (SBM) by the precorrected-FFT (PFFT) for large-scale three-dimensional potential problems. The SBM with the GMRES solver requires computational complexity, where N is the number of the unknowns. To speed up the SBM, the PFFT is employed to accelerate the SBM matrix-vector multiplication at each iteration step of the GMRES. Consequently, the computational complexity can be reduced to 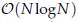. Several numerical examples are presented to validate the developed PFFT accelerated SBM (PFFT-SBM) scheme, and the results are compared with those of the SBM without the PFFT and the analytical solutions. It is clearly found that the present PFFT-SBM is very efficient and suitable for 3D large-scale potential problems.

Keywords

Singular boundary methodprecorrected-FFTfast matrix algorithmthree-dimensional potential problemslarge-scale

MSC classification

Secondary: 65M70: Spectral, collocation and related methods 65N35: Spectral, collocation and related methods 65T50: Discrete and fast Fourier transforms
Type
Research Article
Information
Communications in Computational Physics , Volume 22 , Issue 2 , August 2017 , pp. 460 - 472
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Chen, W., Singular boundary method: a novel, simple, meshfree, boundary collocation numerical method (in Chinese), ACTA MECH SOLIDA SIN 30 (2009), 592–599.Google Scholar
[2] Fu, Z., Chen, W., Chen, J. T., and Qu, W., Singular Boundary Method: Three Regularization Approaches and Exterior Wave Applications, CMES-COMP MODEL ENG 99 (2014), 417–443.Google Scholar
[3] Gu, Y., Gao, H., Chen, W., Liu, C., Zhang, C., and He, X., Fast-multipole accelerated singular boundary method for large-scale three-dimensional potential problems, INT J HEAT MASS TRAN 90 (2015), 291–301.CrossRefGoogle Scholar
[4] Saad, Y., and Schultz, M.H., GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems, SIAM J Sci and Stat Comput 7 (1986), 856–869.Google Scholar
[5] G. L, , and R. V, , A fast algorithmfor particle simulations, J COMPUT PHYS 72 (1987), 325–348.Google Scholar
[6] G. L, , and R. V, , A new version of the fast multipole method for the Laplace equation in three dimensions, ACTA NUMER 6 (1997), 229–269.Google Scholar
[7] Qu, W., Chen, W., and Gu, Y., Fast multipole accelerated singular boundary method for the 3D Helmholtz equation in low frequency regime, COMPUT MATH APPL 70 (2015), 679–690.Google Scholar
[8] P. J. R, , and W. J. K, , A precorrected-FFT method for electrostatic analysis of complicated 3-d structures, IEEE T COMPUT AID D 16 (1997), 1059–1072.Google Scholar
[9] Yan, Z. Y., Zhang, J., and Ye, W., Rapid solution of 3-D oscillatory elastodynamics using the pFFT accelerated BEM, ENG ANAL BOUND ELEM 34 (2010), 956–962.Google Scholar
[10] Ding, J., and Ye, W., A fast integral approach for drag force calculation due to oscillatory slip Stokes flows, INT J NUMER METH ENG 60 (2004), 1535–1567.CrossRefGoogle Scholar
[11] Masters, N., and Ye, W., Fast BEM Solution for Coupled 3D Electrostatic and Linear Elastic Problems, ENG ANAL BOUND ELEM 28 (2004), 1175C1186.CrossRefGoogle Scholar
[12] Ye, W., Wang, X., Hemmert, W., Freeman, D., and White, J., Air damping in laterally oscillating micro-resonators: A Numerical and Experimental Study, J MICROELECTROMECH S 12 (2003), 557–566.Google Scholar
[13] Xiao, J., Ye, W., Cai, Y., and Zhang, J., Precorrected FFT accelerated BEM for large-scale transient elastodynamic analysis using frequency-domain approach, INT J NUMER METH ENG 90 (2012), 116–134.Google Scholar
[14] Chen, Z., Chai, S., Yang, H., and Mao, J., Precorrected-FFT method for EM scattering from composite metallicdielectric objects, CHINESE SCI BULL 55 (2010), 656–663.Google Scholar
[15] Liua, Y., Nishimurab, N., and Otanib, Y., Large-scale modeling of carbon-nanotube composites by a fast multipole boundary element method, COMP MATER SCI 34 (2005), 173–187.CrossRefGoogle Scholar
[16] Jiang, S.-c., Teng, B., Gou, Y., and Ning, D.-z., A precorrected-FFT higher-order boundary element method for waveCbody problems, ENG ANAL BOUND ELEM 36 (2012), 404–415.Google Scholar
[17] Yan, H., and Liu, Y., An efficient high-order boundary element method for nonlinear waveCwave and wave-body interactions, J COMPUT PHYS 230 (2011), 402–424.Google Scholar
[18] Yan, Z., Simulation of acoustic scattering by the fast BEM approach, J HYDRODYN 22 (2010), 948–953.Google Scholar
[19] Yan, Z., and Gao, X., The development of the pFFT accelerated BEM for 3-D acoustic scattering problems based on the Burton and Miller's integral formulation, ENG ANAL BOUND ELEM 37 (2013), 409–418.CrossRefGoogle Scholar
[20] Chen, W., and Fu, Z., A method of fundamental solutions without fictitious boundary, ENG ANAL BOUND ELEM 34 (2010), 530–532.CrossRefGoogle Scholar