Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T05:48:38.976Z Has data issue: false hasContentIssue false
  • English
  • Français

A Numerical Analysis of the Weak Galerkin Method for the Helmholtz Equation with High Wave Number

Part of: Partial differential equations, boundary value problems Optics, electromagnetic theory - General

Published online by Cambridge University Press:  03 May 2017

Yu Du  and
Zhimin Zhang
Yu Du*
Affiliation:
Beijing computational science research center, Beijing 100193, P.R. China
Zhimin Zhang*
Affiliation:
Beijing computational science research center, Beijing 100193, P.R. China Department of Mathematics, Wayne State University, Detroit, MI 48202, USA
*
*Corresponding author. Email addresses:[email protected], [email protected] (Y. Du), [email protected], [email protected] (Z. Zhang)
*Corresponding author. Email addresses:[email protected], [email protected] (Y. Du), [email protected], [email protected] (Z. Zhang)
Get access

Abstract

We study the error analysis of the weak Galerkin finite element method in [24, 38] (WG-FEM) for the Helmholtz problem with large wave number in two and three dimensions. Using a modified duality argument proposed by Zhu and Wu, we obtain the pre-asymptotic error estimates of the WG-FEM. In particular, the error estimates with explicit dependence on the wave number k are derived. 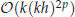This shows that the pollution error in the broken H1-norm is bounded by under mesh condition k7/2h2≤C0 or (kh)2+k(kh)p+1≤C0, which coincides with the phase error of the finite element method obtained by existent dispersion analyses. Here h is the mesh size, p is the order of the approximation space and C0 is a constant independent of k and h. Furthermore, numerical tests are provided to verify the theoretical findings and to illustrate the great capability of the WG-FEM in reducing the pollution effect.

Keywords

Weak Galerkin finite element methodHelmholtz equationlarge wave numberstabilityerror estimates

MSC classification

Secondary: 65N12: Stability and convergence of numerical methods 65N15: Error bounds 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods 78A40: Waves and radiation
Type
Research Article
Information
Communications in Computational Physics , Volume 22 , Issue 1 , July 2017 , pp. 133 - 156
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ainsworth, M., Discrete dispersion relation for hp-version finite element approximation at high wave number, SIAM J. Numer. Anal., 42 (2004), pp. 553–575.CrossRefGoogle Scholar
[2] Aziz, A. and Kellogg, R., A scattering problem for the Helmholtz equation, in Advances in Computer Methods for Partial Differential Equations-III, vol. 1, 1979, pp. 93–95.Google Scholar
[3] Babuška, I., Ihlenburg, F., Paik, E., and Sauter, S., A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution, Comput. Methods Appl. Mech. Engrg., 128 (1995), pp. 325–359.CrossRefGoogle Scholar
[4] Babuška, I. and Sauter, S., Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers?, SIAM Rev., 42 (2000), pp. 451–484.Google Scholar
[5] Brenner, S. and Scott, L., The mathematical theory of finite element methods, Springer, New York, third ed., 2008.CrossRefGoogle Scholar
[6] Chen, H., Lu, P., and Xu, X., A hybridizable discontinuous Galerkin method for the Helmholtz equation with high wave number, SIAM J. Numer. Anal., 51 (2013), pp. 2166–2188.CrossRefGoogle Scholar
[7] Ciarlet, P. G., The finite element method for elliptic problems, North-Holland Pub. Co., New York, 1978.Google Scholar
[8] Demkowicz, L., Gopalakrishnan, J., Muga, I., and Zitelli, J., Wavenumber explicit analysis of a DPG method for the multidimensional Helmholtz equation, Comput. Methods Appl. Mech. Engrg., 214 (2012), pp. 126–138.CrossRefGoogle Scholar
[9] Deraemaeker, A., Babuška, I., and Bouillard, P., Dispersion and pollution of the FEM solution for the Helmholtz equation in one, two and three dimensions, Internat. J. Numer. Methods Engrg., 46 (1999), pp. 471–499.3.0.CO;2-6>CrossRefGoogle Scholar
[10] Douglas, J. Jr, Santos, J., and Sheen, D., Approximation of scalar waves in the space-frequency domain, Math. Models Methods Appl. Sci., 4 (1994), pp. 509–531.CrossRefGoogle Scholar
[11] Du, Y. and Wu, H., Preasymptotic error analysis of higher order fem and cip-fem for Helmholtz equation with high wave number, SIAM J. Numer. Anal., 53 (2015), pp. 782–804.CrossRefGoogle Scholar
[12] Du, Y. and Zhu, L., Preasymptotic error analysis of high order interior penalty discontinuous Galerkin methods for the Helmholtz equation with high wave number, J. Sci. Comput., 67 (2016), pp. 130–152.CrossRefGoogle Scholar
[13] Engquist, B. and Majda, A., Radiation boundary conditions for acoustic and elastic wave calculations, Comm. Pure Appl. Math., 32 (1979), pp. 313–357.CrossRefGoogle Scholar
[14] Feng, X. and Wu, H., Discontinuous Galerkin methods for the Helmholtz equation with large wave numbers, SIAM J. Numer. Anal., 47 (2009), pp. 2872–2896.CrossRefGoogle Scholar
[15] Feng, X. and Wu, H., hp-discontinuous Galerkin methods for the Helmholtz equation with large wave number, Math. Comp., 80 (2011), pp. 1997–2024.CrossRefGoogle Scholar
[16] Harari, I., Reducing spurious dispersion, anisotropy and reflection in finite element analysis of time-harmonic acoustics, Comput. Meth. Appl. Mech. Engrg., 140 (1997), pp. 39–58.CrossRefGoogle Scholar
[17] Ihlenburg, F., Finite element analysis of acoustic scattering, vol. 132 of Applied Mathematical Sciences, Springer-Verlag, New York, 1998.CrossRefGoogle Scholar
[18] Ihlenburg, F. and Babuška, I., Finite element solution of the Helmholtz equation with high wave number. I. The h-version of the FEM, Comput. Math. Appl., 30 (1995), pp. 9–37.CrossRefGoogle Scholar
[19] Ihlenburg, F. and Babuška, I., Finite element solution of the Helmholtz equation with high wave number. II. The h-p version of the FEM, SIAM J. Numer. Anal., 34 (1997), pp. 315–358.CrossRefGoogle Scholar
[20] Melenk, J., Parsania, A., and Sauter, S., General DG-methods for highly indefinite Helmholtz problems, Journal of Scientific Computing, 57 (2013), pp. 536–581.CrossRefGoogle Scholar
[21] Melenk, J. M. and Sauter, S., Convergence analysis for finite element discretizations of the Helmholtz equation with Dirichlet-to-Neumann boundary conditions, Math. Comp., 79 (2010), pp. 1871–1914.CrossRefGoogle Scholar
[22] Melenk, J. M. and Sauter, S., Wavenumber explicit convergence analysis for Galerkin discretizations of the Helmholtz equation, SIAM J. Numer. Anal., 49 (2011), pp. 1210–1243.CrossRefGoogle Scholar
[23] Monk, P., Finite element methods for Maxwell's equations, Oxford University Press, New York, 2003.CrossRefGoogle Scholar
[24] Mu, L., Wang, J., and Ye, X., A new weak Galerkin finite element method for the Helmholtz equation, IMA Journal of Numerical Analysis, 35 (2014), pp. 1228–1255.Google Scholar
[25] Mu, L., Wang, J., Ye, X., and Zhao, S., A numerical study on the weak Galerkin method for the helmholtz equation, Communications in Computational Physics, 15 (2014), pp. 1461–1479.CrossRefGoogle Scholar
[26] Schatz, A., An observation concerning Ritz–Galerkin methods with indefinite bilinear forms, Math. Comp., 28 (1974), pp. 959–962.CrossRefGoogle Scholar
[27] Shen, J. and Wang, L., Analysis of a spectral-Galerkin approximation to the Helmholtz equation in exterior domains, SIAM J. Numer. Anal., 45 (2007), pp. 1954–1978.CrossRefGoogle Scholar
[28] Thompson, L., A review of finite-element methods for time-harmonic acoustics, J. Acoust. Soc. Am., 119 (2006), pp. 1315–1330.CrossRefGoogle Scholar
[29] Thompson, L. and Pinsky, P., Complex wavenumber Fourier analysis of the p-version finite element method, Comput. Mech., 13 (1994), pp. 255–275.CrossRefGoogle Scholar
[30] Wang, J. and Wang, C., Weak Galerkin finite element methods for elliptic pdes (in chinese), Sci. Sin. Math, 45 (2015), pp. 1061–1092.CrossRefGoogle Scholar
[31] Wang, J. and Ye, X., A weak Galerkin finite element method for second-order elliptic problems, J. Comp. Appl. Math., 214 (2013), pp. 103–115.CrossRefGoogle Scholar
[32] Wu, H., Pre-asymptotic error analysis of CIP-FEM and FEM for Helmholtz equation with high wave number. Part I: Linear version, IMA J. Numer. Anal., 34 (2014), pp. 1266–1288.CrossRefGoogle Scholar
[33] Zhu, L. and Du, Y., Pre-asymptotic error analysis of hp-interior penalty discontinuous Galerkin methods for the Helmholtz equation with large wave number, Comput. Math. Appl., 70 (2015), pp. 917–933.CrossRefGoogle Scholar
[34] Zhu, L. and Wu, H., Pre-asymptotic error analysis of CIP-FEM and FEM for Helmholtz equation with high wave number. Part II: hp version, SIAM J. Numer. Anal., 51 (2013), pp. 1828–1852.CrossRefGoogle Scholar
[35] Zitelli, J., Muga, I., Demkowicz, L., Gopalakrishnan, J., Pardo, D., and Calo, V., A class of discontinuous Petrov-Galerkin methods. Part IV: The optimal test norm and time-harmonic wave propagation in 1D, J. Comput. Phys., 230 (2011), pp. 2406–2432.CrossRefGoogle Scholar
[36] Zhang, R. and Zhai, Q., A weak Galerkin finite element scheme for the biharmonic equa- tions by using polynomials of reduced order, J. Sci. Comput., 64(2015), pp. 559–585.CrossRefGoogle Scholar
[37] Zhai, Q., Zhang, R. and Mu, L., A new weak Galerkin finite element scheme for the Brinkman model, Commun. Comput. Phys., 19(2016), pp. 1409–1434.CrossRefGoogle Scholar
[38] Mu, L., Wang, J., Ye, X. and Zhang, S., A weak Galerkin finite element method for the Maxwell equations, (English summary) J. Sci. Comput., 65(2015), pp. 363–386.CrossRefGoogle Scholar