Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T10:09:22.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations

Part of: General theory in ordinary differential equations Real functions Miscellaneous topics - Partial differential equations Computational aspects Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  07 February 2017

Shidong Jiang ,
Jiwei Zhang ,
Qian Zhang  and
Zhimin Zhang
Shidong Jiang*
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102, USA
Jiwei Zhang*
Affiliation:
Beijing Computational Science Research Center, Beijing 100093, China
Qian Zhang*
Affiliation:
Beijing Computational Science Research Center, Beijing 100093, China
Zhimin Zhang*
Affiliation:
Beijing Computational Science Research Center, Beijing 100093, China Department of Mathematics, Wayne State University, Detroit, MI 48202, USA
*
*Corresponding author. Email addresses:[email protected] (S. Jiang), [email protected] (J. Zhang), [email protected] (Q. Zhang), [email protected] (Z. Zhang)
*Corresponding author. Email addresses:[email protected] (S. Jiang), [email protected] (J. Zhang), [email protected] (Q. Zhang), [email protected] (Z. Zhang)
*Corresponding author. Email addresses:[email protected] (S. Jiang), [email protected] (J. Zhang), [email protected] (Q. Zhang), [email protected] (Z. Zhang)
*Corresponding author. Email addresses:[email protected] (S. Jiang), [email protected] (J. Zhang), [email protected] (Q. Zhang), [email protected] (Z. Zhang)
Get access

Abstract

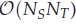The computational work and storage of numerically solving the time fractional PDEs are generally huge for the traditional direct methods since they require total memory and work, where NT and NS represent the total number of time steps and grid points in space, respectively. To overcome this difficulty, we present an efficient algorithm for the evaluation of the Caputo fractional derivative 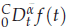of order α∈(0,1). The algorithm is based on an efficient sum-of-exponentials (SOE) approximation for the kernel t–1–α on the interval [Δt, T] with a uniform absolute error ε. We give the theoretical analysis to show that the number of exponentials Nexp needed is of order 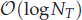for T≫1 or 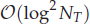for TH1 for fixed accuracy ε. The resulting algorithm requires only 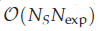storage and 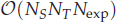work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.

Keywords

Fractional derivativeCaputo derivativesum-of-exponentials approximationfractional diffusion equationfast convolution algorithmstability analysis

MSC classification

Secondary: 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$ 33F05: Numerical approximation and evaluation 35Q40: PDEs in connection with quantum mechanics 35Q55: NLS-like equations (nonlinear Schrödinger) 34A08: Fractional differential equations 35R11: Fractional partial differential equations 26A33: Fractional derivatives and integrals
Type
Research Article
Information
Communications in Computational Physics , Volume 21 , Issue 3 , March 2017 , pp. 650 - 678
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Tao Zhou

References

[1] Alpert, B., Greengard, L., and Hagstrom, T., Rapid evaluation of nonreflecting boundary kernels for time-domain wave propagation, SIAM J. Numer. Anal., 37 (2000), 1138–1164.CrossRefGoogle Scholar
[2] Awotunde, A. A., Ghanam, R. A., and Tatar, N., Artificial boundary condition for a modified fractional diffusion problem, Bound. Value Probl., 1 (2015), 1–17.Google Scholar
[3] Baffet, D. and Hesthaven, Jan S., A Laplace transform based kernel reduction scheme for fractional differential equations, https://infoscience.epfl.ch/record/212955, 2016.Google Scholar
[4] Brunner, H., Han, H., and Yin, D., Artificial boundary conditions and finite difference approximations for a time-fractional diffusion-wave equation on a two-dimensional unbounded spatial domain, J. Comput. Phys., 276 (2014), 541–562.CrossRefGoogle Scholar
[5] Beylkin, G. and Monzón, L., On approximation of functions by exponential sums, Appl. Comput. Harmon. Anal., 19 (2005), 17–48.CrossRefGoogle Scholar
[6] Beylkin, G. and Monzón, L., Approximation by exponential sums revisited, Appl. Comput. Harmon. Anal., 28 (2010), 131–149.CrossRefGoogle Scholar
[7] Brunner, H., Han, H., and Yin, D., The maximum principle for time-fractional diffusion equations and its application, Numer. Funct. Anal. Optim., 36 (2015), 1307–1321.CrossRefGoogle Scholar
[8] Brunner, H., Wu, X. and Zhang, J., Computational Solution of Blow-Up Problems for Semilinear Parabolic PDEs on Unbounded Domains. SIAM J. Sci. Comput., 31(2010), 4478–4496.CrossRefGoogle Scholar
[9] Cao, J.X., Li, C.P. and Chen, Y.Q., High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (II), Frac. Calc. and Appl. Anal. 18.3 (2015), 735–761.Google Scholar
[10] Cao, J. and Xu, C., A high order scheme for the numerical solution of the fractional ordinary differential equations, J. Comput. Phys., 238 (2013), 154–168.CrossRefGoogle Scholar
[11] Chen, C., Liu, F., Anh, V., and Turner, I., Numerical methods for solving a two-dimensional variable-order anomalous subdiffusion equation, Math. Comp., 81 (2012), 345–366.CrossRefGoogle Scholar
[12] Cui, M., Compact finite difference method for the fractional diffusion equation, J. Comput. Phys., 228 (2009), 7792–7804.CrossRefGoogle Scholar
[13] Cui, M., Compact alternating direction implicit method for two-dimensional time fractional diffusion equation, J. Comput. Phys., 231 (2012), 2621–2633.CrossRefGoogle Scholar
[14] Dea, J. R., Absorbing boundary conditions for the fractional wave equation, Appl. Math. Comput., 219 (2013), 9810–9820.Google Scholar
[15] Gao, G. H., Sun, Z. Z., and Zhang, Y. N., A finite difference scheme for fractional sub-diffusion equations on an unbounded domain using artificial boundary conditions, J. Comput. Phys., 231 (2012), 2865–2879.Google Scholar
[16] Gao, G. H. and Sun, Z. Z., The finite difference approximation for a class of fractional subdiffusion equations on a space unbounded domain, J. Comput. Phys., 236 (2013), 443–460.CrossRefGoogle Scholar
[17] Gao, G. H. and Sun, Z. Z., A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications, J. Comput. Phys., 259 (2014), 33–50.Google Scholar
[18] Ghaffari, R. and Hosseini, S. M., Obtaining artificial boundary conditions for fractional subdiffusion equation on space two-dimensional unbounded domains, Comput. Math. Appl., 68 (2014), 13–26.CrossRefGoogle Scholar
[19] Guo, B. L., Xu, Q. and Zhu, A. L. A second-order finite difference method for two-dimensional fractional percolation equations, Commun. Comput. Phys., 19 (2016), 733–757.CrossRefGoogle Scholar
[20] Greengard, L. and Lin, P., Spectral approximation of the free-space heat kernel, Appl. Comput. Harmon. Anal., 9 (2000), 83–97.Google Scholar
[21] Greengard, L. and Strain, J., A fast algorithm for the evaluation of heat potentials, Comm. Pure Appl. Math., 43 (1990), 949–963.Google Scholar
[22] Han, H. and Wu, X., Artificial Boundary Method, Tsinghua Univ. Press, 2013.CrossRefGoogle Scholar
[23] Huang, X. and Yin, D., Artificial boundary conditions and finite difference approximations for a time-fractional diffusion-wave equation on high dimensional unbounded spatial domain, J. Comput. Phys., to appear.Google Scholar
[24] Jiang, S. and Greengard, L., Efficient representation of nonreflecting boundary conditions for the time-dependent Schrödinger equation in two dimensions, Comm. Pure Appl. Math., 61 (2008), 261–288.Google Scholar
[25] Jiang, S., Greengard, L., and Bao, W., Fast and accurate evaluation of nonlocal Coulomb and dipole-dipole interactions via the nonuniform FFT, SIAM J. Sci. Comput., 36.5 (2014), B777–B794.Google Scholar
[26] Jiang, S., Greengard, L., and Wang, S., Efficient sum-of-exponentials approximations for the heat kernel and their applications, Adv. Comput. Math., 41.3 (2015), 529–551.CrossRefGoogle Scholar
[27] Ke, R., Ng, M., and Sun, H., A fast direct method for block triangular Toeplitz-like with tridiagonal block systems from time-fractional partial differential equations, J. Comput. Phys., 303 (2015), 203–211.CrossRefGoogle Scholar
[28] Kilbas, A., Srivastava, H., and Trujillo, J., Theory and Applications of Fractional Differential Equations, Elesvier Science and Technology, Boston, 2006.Google Scholar
[29] Langlands, T. and Henry, B., Fractional chemotaxis diffusion equations, Phys. Rev. E, 81 (2010), 051102.Google Scholar
[30] Langlands, T. and Henry, B., The accuracy and stability of an implicit solution method for the fractional diffusion equation, J. Comput. Phys., 205 (2005), 719–736.CrossRefGoogle Scholar
[31] Lei, S. and Sun, H., A circulant preconditioner for fractional diffusion equations, J. Comput. Phys., 242 (2013), 715–725.CrossRefGoogle Scholar
[32] Li, C., Deng, W., and Wu, Y., Numerical analysis and physical simulations for the time fractional radial diffusion equation, Comput. Math. Appl., 62 (2011), 1024–1037.CrossRefGoogle Scholar
[33] Li, C., Chen, A., and Ye, J., Numerical approaches to fractional calculus and fractional ordinary differential equation, J. Comput. Phys., 230 (2011), 3352–3368.CrossRefGoogle Scholar
[34] Li, C., Wu, R. and Ding, H., High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations, Commun. Appl. Indu. Math., 6.2, e-536 (2014), 1–32.Google Scholar
[35] Li, D. and Zhang, J., Efficient implementation to numerically solve the nonlinear time fractional parabolic problems on unbounded spatial domain, J. Comput. Phys., 322 (2016), 415–428.Google Scholar
[36] Li, D., Zhang, C., Ran, M., A linear finite difference scheme for generalized time fractional Burgers equation, Appl. Math. Model., 40 (2016), 6069–6081.CrossRefGoogle Scholar
[37] Li, H., Cao, J., Li, C., High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (III), J. Comput. Appl. Math., 299 (2016), 159–175.Google Scholar
[38] Li, J., A fast time stepping method for evaluating fractional integrals, SIAM J. Sci. Comput., 31 (2010), 4696–4714.Google Scholar
[39] Li, L.M., Xu, D., Alternating direction implicit Galerkin finite element method for the two-dimensional time fractional evolution equation, Numer. Math. Theor. Meth. Appl., 7 (2014), 41–57.Google Scholar
[40] Lin, Y. and Xu, C., Finite difference/spectral approximations for the time-fractional diffusion equation, J. Comput. Phys., 225 (2007), 1533–1552.CrossRefGoogle Scholar
[41] Lin, Y., Li, X., and Xu, C., Finite difference/spectral approximations for the fractional cable equation, Math. Comp., 80 (2011), 1369–1396.Google Scholar
[42] Lin, Y. and Xu, C., Finite difference/spectral approximations for time-fractional diffusion equation, J. Comput. Phys., 225 (2007), 1533–1552.CrossRefGoogle Scholar
[43] Lu, X., Sun, H., and Pang, H., Fast approximate inversion of a block triangular Toeplitz matrix with applications to fractional subdiffusion equations, J. Numer. Lin. Alg. Appl., 22 (2015), 866–882.CrossRefGoogle Scholar
[44] Lubich, C. and Schädle, A., Fast convolution for nonreflecting boundary conditions, SIAM J. Sci. Comput. 24 (2002) 161–182.CrossRefGoogle Scholar
[45] McLean, W., Fast summation by interval clustering for an evolution equation with memory, SIAM J. Numer. Anal., 34.6 (2012), 3039–3056.Google Scholar
[46] Metzler, R. and Klafter, J., The random walks guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 339 (2000).CrossRefGoogle Scholar
[47] Odibat, Z., Approximations of fractional integrals and Caputo fractional derivatives, Appl. Math. Comput., 178 (2006), 527–533.Google Scholar
[48] Oldham, K. B. and Spanier, J., The Fractional Calculus, Academic Press, New York, 1974.Google Scholar
[49] Olver, F. W. J., Lozier, D. W., Boisvert, R. F., and Clark, C. W., editors. NIST Handbook of Mathematical Functions, Cambridge University Press, New York, NY, 2010.Google Scholar
[50] Pang, H. and Sun, H., Multigrid method for fractional diffusion equations, J. Comput. Phys., 231 (2012), 693–703.CrossRefGoogle Scholar
[51] Podlubny, I., Fractional Differential Equations, Academic Press, San Diego, 1999.Google Scholar
[52] Sun, Z. and Wu, X., A fully discrete difference scheme for a diffusion-wave system, Appl. Numer. Math., 56 (2006), 193–209.CrossRefGoogle Scholar
[53] Wang, H., Wang, K., and Sircar, T., A direct finite difference method for fractional diffusion equations, J. Comput. Phys., 229 (2010), 8095–8104.Google Scholar
[54] Wang, H. and Treena, S. B., A fast finite difference method for two-dimensional space-fractional diffusion equations, SIAM J. Sci. Comput., 34 (2012), 2444–2458.Google Scholar
[55] Xu, K. and Jiang, S., A bootstrap method for sum-of-poles approximations, J. Sci. Comput., 55 (2013), 16–39.CrossRefGoogle Scholar
[56] Zhang, J., Xu, Z., Wu, X., Unified approach to split absorbing boundary conditions for nonlinear Schrödinger equations, Phys. Rev. E, 78 (2008), 026709.CrossRefGoogle ScholarPubMed
[57] Zhang, J., Xu, Z., Wu, X., Unified approach to split absorbing boundary conditions for nonlinear Schröinger equations: Two dimensional case, Phys. Rev. E, 79 (2009), 046711.CrossRefGoogle Scholar
[58] Zhang, Q., Zhang, J., Jiang, S., Zhang, Z., Numerical solution to a linearized time fractional KdV equation on unbounded domains, accepted by Math. Comput., 2016.Google Scholar
[59] Zheng, C., Approximation, stability and fast evaluation of exact artificial boundary condition for one-dimensional heat equation, J. Comput. Math., 25 (2007), 730–745.Google Scholar