Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T17:35:57.709Z Has data issue: false hasContentIssue false
  • English
  • Français

An Adaptive Finite Element Method with Hybrid Basis for Singularly Perturbed Nonlinear Eigenvalue Problems

Part of: General mathematical topics and methods in quantum theory Partial differential equations, boundary value problems Equations of mathematical physics and other areas of application Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  01 February 2016

Ye Li
Ye Li*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China
*
*Corresponding author. Email address:[email protected] (Y.Li)
Get access

Abstract

In this paper, we propose an uniformly convergent adaptive finite element method with hybrid basis (AFEM-HB) for the discretization of singularly perturbed nonlinear eigenvalue problems under constraints with applications in Bose-Einstein condensation (BEC) and quantum chemistry. We begin with the time-independent Gross-Pitaevskii equation and show how to reformulate it into a singularly perturbed nonlinear eigenvalue problem under a constraint. Matched asymptotic approximations for the problem are reviewed to confirm the asymptotic behaviors of the solutions in the boundary/interior layer regions. By using the normalized gradient flow, we propose an adaptive finite element with hybrid basis to solve the singularly perturbed nonlinear eigenvalue problem. Our basis functions and the mesh are chosen adaptively to the small parameter ε. Extensive numerical results are reported to show the uniform convergence property of our method. We also apply the AFEM-HB to compute the ground and excited states of BEC with box/harmonic/optical lattice potential in the semiclassical regime (0 <ε≪C 1). In addition, we give a detailed error analysis of our AFEM-HB to a simpler singularly perturbed two point boundary value problem, show that our method has a minimum uniform convergence order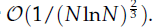

Keywords

Adaptive finite elementhybrid basisnonlinear eigenvalue problemsingularly perturbed problemBose-Einstein condensationuniform convergence

MSC classification

Secondary: 35P30: Nonlinear eigenvalue problems, nonlinear spectral theory 35Q55: NLS-like equations (nonlinear Schrödinger) 65N25: Eigenvalue problems 65N06: Finite difference methods 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods 81Q05: Closed and approximate solutions to the Schrödinger, Dirac, Klein-Gordon and other equations of quantum mechanics
Type
Research Article
Information
Communications in Computational Physics , Volume 19 , Issue 2 , February 2016 , pp. 442 - 472
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Adhikari, S. K., Numerical solution of the two-dimensional Gross-Pitaevskii equation for trapped interacting atoms, Phys. Lett. A, 265 (2000), 91.Google Scholar
[2]Aftalion, A. and Du, Q., Vortices in a rotating Bose-Einstein condensate: Critical angular velocities and energy diagrams in the Thomas-Fermi regime, Phys. Rev. A, 64 (2001), 063603.Google Scholar
[3]Anderson, M. H., Ensher, J. R., Matthewa, M. R., Wieman, C. E. and Cornell, E. A., Observation of Bose-Einstein condensation in a dilute atomic vapor, Science, 269 (1995), 198–201.Google Scholar
[4]Bao, W., Ground states and dynamics of multi-component Bose-Einstein condensates, Multiscale Modeling and Simulation, 2 (2004), 210–236.Google Scholar
[5]Bao, W. and Cai, Y., Mathematical theory and numerical methods for Bose-Einstein condensation, Kinet. Relat. Mod., 6 (2013), 1–135.CrossRefGoogle Scholar
[6]Bao, W., Cai, Y. and Wang, H., Efficient numerical methods for computing ground states and dynamics of dipolar Bose-Einstein condensates, J. Comput. Phys., 229 (2010), 7874–7892.Google Scholar
[7]Bao, W., Chern, I-L. and Zhang, Y., Efficient methods for computing ground states of spin-1 Bose-Einstein condensates based on their characterizations, J. Comput. Phys., 253 (2013), 189–208.Google Scholar
[8]Bao, W. and Chai, M. H., A uniformly convergent numerical method for singularly perturbed nonlinear eigenvalue problem, Commun. Comput. Phys. 4 (2008), 135–160.Google Scholar
[9]Bao, W. and Du, Q., Computing the ground state solution of Bose-Einstein condensates by a normalized gradient flow, SIAM J. Sci. Comput., 25 (2004), 1674–1697.Google Scholar
[10]Bao, W., Chern, I.-L. and Lim, F. Y., Efficient and spectrally accurate numerical methods for computing ground and first excited states in Bose-Einstein condensates, J. Comput. Phys., 219 (2006), 836–854.CrossRefGoogle Scholar
[11]Bao, W., Jaksch, D. and Markowich, P. A., Numerical solution of the Gross-Pitaevskii equation for Bose-Einstein condensation, J. Comput. Phys., 187 (2003), 318–342.Google Scholar
[12]Bao, W. and Lim, F. Y., Computing ground states of spin-1 Bose-Einstein Condensates by the normalized gradient flow, SIAM J. Sci. Comput., 34 (2008), 1985–2008.Google Scholar
[13]Bao, W., Lim, F. Y. and Zhang, Y., Energy and chemical potential asymptotics for the ground state of Bose-Einstein condensates in the semiclassical regime, Bull. Inst. Math., Academia Sinica, 2 (2007), 495–532.Google Scholar
[14]Bao, W. and Tang, W., Ground state solution of trapped interacting Bose-Einstein condensate by directly minimizing the energy functional, J. Comput. Phys., 187 (2003), 230–254.CrossRefGoogle Scholar
[15]Bao, W. and Wang, H., A mass and magnetization conservative and energy diminishing numerical method for computing ground state of spin-1 Bose-Einstein condensates, SIAM J. Numer. Anal., 45 (2007), 2177–2200.CrossRefGoogle Scholar
[16]Bao, W., Wang, H. and Markowich, P. A., Ground, symmetric and central vortex states in rotating Bose-Einstein condensates, Commun. Math. Sci., 3 (2005), 57–88.Google Scholar
[17]Chen, H., He, L. and Zhou, A., Finite element approximations of nonlinear eigenvalue problems in quantumn physics, Comput. Methods Appl. Mech. Engrg., 200 (2011), 1846–1865.Google Scholar
[18]Ciarlet, P. G., The Finite Element Method for Elliptic Problems, North-Holland, Amsterdam, 1978.Google Scholar
[19]Cerimele, M. M., Chiofalo, M. L., Pistella, F., Succi, S. and Tosi, M. P., Numerical solution of the Gross-Pitaevskii equation using an explicit finite-difference scheme: An application to trapped Bose-Einstein condensates, Phys. Rev. E, 62, 1382 (2000).CrossRefGoogle ScholarPubMed
[20]Chang, S.-M., Lin, W.-W and Shieh, S.-F., Gauss-Seidel-type methods for energy states of a multi-component Bose-Einstein condensate, J. Comput. Phys., 202 (2005), 367–390.Google Scholar
[21]Chin, R. C. Y. and Krasny, R., A hybrid asymptotic finite element method for stiff two-point boundary value problems. SIAM J. Sci. Comput., 4 (1983), 229–243.CrossRefGoogle Scholar
[22]Chiofalo, M. L., Succi, S. and Tosi, M. P., Ground state of trapped interacting Bose-Einstein condensates by an explicit imaginary-time algorithm, Phys. Rev. E, 62 (2000), 7438.Google Scholar
[23]Dalfovo, F. and Stringari, S., Bosons in anisotropic traps: Ground state and vortices, Phys. Rev. A, 53 (1996), 2477.Google Scholar
[24]Dai, X., Xu, J. and Zhou, A., Convergence and optimal complexity of adaptive finite element eigenvalue computations, Numer. Math., 110 (2008), 313–355.Google Scholar
[25]Dodd, R. J., Approximate solutions of the nonlinear Schrodinger equation for ground and excited states of Bose-Einstein condensates, J. Res. Natl. Inst. Stan., 101 (1996), 545.Google Scholar
[26]Edwards, M. and Burnett, K., Numerical solution of the nonlinear Schrodinger equation for small samples of trapped neutral atoms, Phys. Rev. A, 51 (1995), 1382.Google Scholar
[27]Han, H. and Huang, Z., Tailored finite point method for steady-state reaction-diffusion equation, Commun. Math. Sci., 8 (2010), 887–899.CrossRefGoogle Scholar
[28]Han, H. and Huang, Z., Tailored finite point method based on exponential bases for convection-diffusion-reaction equation, Math. Comp., 82 (2013), 213–226.Google Scholar
[29]Han, H. and Huang, Z, The Tailored Finite Point Method, Comput. Methods Appl. Math. 14 (2014), 321–345.Google Scholar
[30]Han, H., Huang, Z. and Kellogg, B., A Tailored finite point method for a singular perturbation problem on an unbounded domain, J. Sci. Comput., 36 (2008), 243–261.Google Scholar
[31]Han, H., Miller, J. J. H. and Tang, M., A parameter-uniform tailored finite point method for singularly perturbed linear ODE systems, J. Comput. Math. 31 (2013), 422–438.Google Scholar
[32]Jiang, L. and Yue, X., Local exponentially fitted fnite element schemes for singularly perturbed convection-diffusion problems, J. Comput. Appl. Math., 132 (2001), 277–293.Google Scholar
[33]Lin, R. and Stynes, M., A balanced finite element method for singularly perturbed reaction diffusion problems, SIAM J. Numer. Anal., 50 (2012), 2729–2743.CrossRefGoogle Scholar
[34]Melenk, J. M., hp-finite element methods for singular perturbations, Lecture Notes in Mathematics, 1796. Springer-Verlag, Berlin, 2002.Google Scholar
[35]Miller, J. J. H., ORiordan, E. and Shishkin, G. I., Fitted Numerical Mehtods for Sigular Perturbation Problems, World Scientific, 1996.Google Scholar
[36]Miller, J. J. H., ORiordan, E. and Shishkin, G. I., On piecewise-uniform meshes for upwindand central-difference operators for solving singularly perturbed problems, IMA J. Numer. Anal., 15 (1995), 89–99.Google Scholar
[37]Pitaevskii, L. P. and Stringari, S., Bose-Einstein Condensation, Clarendon Press, 2003.Google Scholar
[38]O'Riordan, E., Stynes, M., A uniformly accurate finite-element method for a singularly perturbed one dimensional reaction-diffusion problem, Math. Comp., 47 (1986), 555–570.Google Scholar
[39]Roos, H. G., Stynes, M. and Tobiska, L., Numerical Methods for Singularly Perturbed Differential Equations, Springer-Verlag, Berlin, 2nd ed., 2008.Google Scholar
[40]Schneider, B. I. and Feder, D. L., Numerical approach to the ground and excited states of a Bose-Einstein condensated gas confined in a completely anisotropic trap, Phys. Rev. A, 59 (1999), 2232.Google Scholar
[41]Shen, L., Xin, J. and Zhou, A., Finite element computation of KPP front speeds in celluar and cats eye flows, J. Sci. comput., 55 (2013), 455–470.Google Scholar
[42]Shen, L. and Zhou, A., A defect correction scheme for finite element eigenvalues with applications to quantum chemistry, SIAM J. Sci. Comput., 28 (2006), 321–338.Google Scholar
[43]Stynes, M., ORiordan, E., An analysis of a singularly perturbed two-point boundary problem using only finite element techniques, Math. Comp., 56 (1991), 663–675.Google Scholar
[44]Qiu, Y., Sloan, D. M. and Tang, T., Numerical solution of a singularly perturbed two-point boundary value problem using equidistribution: analysis of convergence, J. Comput. Appl. Math., 116 (2000), 121–143.Google Scholar
[45]Zhou, A., Finite dimensional approximations for the electronic ground state solution of a molecular system, Math. Methods Appl. Sci., 30 (2007), 429–447.Google Scholar
[46]Zhou, A., An analysis of finite-dimensional approximations for the ground state solution of Bose-Einstein condensates, Nonlinearity, 17 (2004), 541–550.Google Scholar