No CrossRef data available.
Article contents
Vicarious Graphs
Published online by Cambridge University Press: 13 November 2009
Abstract
Let H be some fixed graph. We call a graph Gvicarious for H if G is maximal H-free and, for every edge e of G, there is an edge f not in G such that G − e + f is also H-free. We demonstrate various properties of vicarious graphs and several examples are given. It is conjectured that a graph of order n which is vicarious for K3 has size at most (1/4 + o(1))(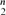 ).
).
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 819 - 827
- Copyright
- Copyright © Cambridge University Press 2009
References
[1]Erdős, P. (1967) Some recent results on extremal problems in graph theory: Results. In Theory of Graphs, Proc. International Symposium, Rome 1966 (Rosenstiehl, P., ed.), Gordon and Breach, New York, Dunod, Paris, pp. 118–123.Google Scholar
[2]Erdős, P. (1968) On some new inequalities concerning extremal properties of graphs. In Theory of Graphs, Proc. Colloquium, Tihany 1966 (Erdős, P. and Katona, G., eds), Academic Press, New York, pp. 77–81.Google Scholar
[3]Erdős, P., Faudree, R. J., Gyárfás, A. and Schelp, R. H. (1991) Odd cycles in graphs of given minimum degree. In Graph Theory, Combinatorics and Applications, Vol. 1, Proc. International Conference, Kalamazoo 1988, Wiley-Interscience, New York, pp. 407–418.Google Scholar
[4]Simonovits, M. (1968) A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs, Proc. Colloquium, Tihany 1966 (Erdős, P. and Katona, G., eds), Academic Press, New York, pp. 279–319.Google Scholar


