Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T17:16:41.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Universality of Graphs with Few Triangles and Anti-Triangles

Part of: Graph theory

Published online by Cambridge University Press:  29 July 2015

DAN HEFETZ  and
MYKHAYLO TYOMKYN
DAN HEFETZ
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK (e-mail: [email protected], [email protected])
MYKHAYLO TYOMKYN
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study 3-random-like graphs, that is, sequences of graphs in which the densities of triangles and anti-triangles converge to 1/8. Since the random graph 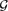$\mathcal{G}$n,1/2 is, in particular, 3-random-like, this can be viewed as a weak version of quasi-randomness. We first show that 3-random-like graphs are 4-universal, that is, they contain induced copies of all 4-vertex graphs. This settles a question of Linial and Morgenstern [10]. We then show that for larger subgraphs, 3-random-like sequences demonstrate completely different behaviour. We prove that for every graph H on n ⩾ 13 vertices there exist 3-random-like graphs without an induced copy of H. Moreover, we prove that for every ℓ there are 3-random-like graphs which are ℓ-universal but not m-universal when m is sufficiently large compared to ℓ.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C60: Isomorphism problems (reconstruction conjecture, etc.) and homomorphisms (subgraph embedding, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 4 , July 2016 , pp. 560 - 576
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alon, N., Fischer, E., Krivelevich, M. and Szegedy, M. (2000) Efficient testing of large graphs. Combinatorica 20 451–476.Google Scholar
[2] Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, third edition, Wiley.Google Scholar
[3] Balister, P. Personal communication.Google Scholar
[4] Bollobás, B. (1998) Modern Graph Theory, corrected edition, Graduate texts in Mathematics, Springer.CrossRefGoogle Scholar
[5] Chung, F. R. K., Graham, R. L. and Wilson, R. M. (1989) Quasi-random graphs. Combinatorica 9 345–362.Google Scholar
[6] Erdős, P. (1962) On the number of complete subgraphs contained in certain graphs. Magyar Tud. Akad. Mat. Kulató Int. Kőzl 7 459–464.Google Scholar
[7] Erdős, P. and Hajnal, A. (1989) Ramsey-type theorems. Discrete Appl. Math. 25 37–52.CrossRefGoogle Scholar
[8] Falgas-Ravry, V. and Vaughan, E. R. (2013) Applications of the semi-definite method to the Turán density problem for 3-graphs. Combin. Probab. Comput. 22 21–54.CrossRefGoogle Scholar
[9] Goodman, A. W. (1959) On sets of acquaintances and strangers at any party. Amer. Math. Monthly 66 778–783.Google Scholar
[10] Linial, N. and Morgenstern, A. Graphs with few 3-cliques and 3-anticliques are 3-universal. J. Graph Theory, to appear. arXiv.org:1306.2020 Google Scholar
[11] Radziszowski, S. (2011) Small Ramsey numbers. Electron. J. Combin. DS1.CrossRefGoogle Scholar
[12] Seinsche, D. (1974) On a property of the class of n-colorable graphs. J. Combin. Theory Ser. B 16 191–193.Google Scholar
[13] Simonovits, M. (1968) A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs: Proc. Colloq., Tihany, 1966, Academic, pp. 279–319.Google Scholar
[14] Thomason, A. (1987) Pseudorandom graphs. In Random Graphs'85: Poznań, 1985, Vol. 144 of North-Holland Mathematics Studies, North-Holland, pp. 307–331.Google Scholar
[15] Thomason, A. (1989) A disproof of a conjecture of Erdős in Ramsey theory. J. London Math. Soc 39 246–255.Google Scholar