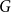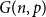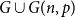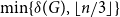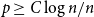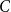1. Introduction and main result
The problem of subgraph containment is one of the most studied questions in extremal and probabilistic combinatorics. In this paper, we are interested in conditions that guarantee the containment of pairwise vertex-disjoint triangles in different graph models. In particular, when a graph
![]() $G$
on
$G$
on
![]() $v(G)$
vertices contains
$v(G)$
vertices contains
![]() $\lfloor v(G)/3 \rfloor$
pairwise vertex-disjoint copies of triangles, we say that
$\lfloor v(G)/3 \rfloor$
pairwise vertex-disjoint copies of triangles, we say that
![]() $G$
contains a triangle factor. We will consider minimum degree conditions in dense graphs, lower bounds on the edge-probability in random graphs, and a combination of both.
$G$
contains a triangle factor. We will consider minimum degree conditions in dense graphs, lower bounds on the edge-probability in random graphs, and a combination of both.
From Mantel’s theorem on the maximum number of edges in a triangle-free graph, it follows that any
![]() $n$
-vertex graph with minimum degree larger than
$n$
-vertex graph with minimum degree larger than
![]() $n/2$
contains a triangle. The first result on the containment of a triangle factor is due to Corrádi and Hajnal [Reference Corrádi and Hajnal11], who proved that any
$n/2$
contains a triangle. The first result on the containment of a triangle factor is due to Corrádi and Hajnal [Reference Corrádi and Hajnal11], who proved that any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G) \ge 2n/3$
contains a triangle factor. From this, it is not hard to derive a more general result for graphs with smaller minimum degree, which was first proved by Dirac [Reference Dirac12].
$\delta (G) \ge 2n/3$
contains a triangle factor. From this, it is not hard to derive a more general result for graphs with smaller minimum degree, which was first proved by Dirac [Reference Dirac12].
Theorem 1.1 (Dirac [Reference Dirac12]). Any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $n/2 \le \delta (G) \le 2n/3$
contains at least
$n/2 \le \delta (G) \le 2n/3$
contains at least
![]() $2\delta (G)-n$
pairwise vertex-disjoint triangles.
$2\delta (G)-n$
pairwise vertex-disjoint triangles.
Given an integer
![]() $m$
with
$m$
with
![]() $n/2 \le m \le 2n/3$
, the tripartite complete graph with parts of size
$n/2 \le m \le 2n/3$
, the tripartite complete graph with parts of size
![]() $2m-n$
,
$2m-n$
,
![]() $n-m$
, and
$n-m$
, and
![]() $n-m$
shows the result is best possible. Moreover, a stability version of Theorem 1.1 was proved by Hladký, Hu, and Piguet [Reference Hladký, Hu and Piguet18].
$n-m$
shows the result is best possible. Moreover, a stability version of Theorem 1.1 was proved by Hladký, Hu, and Piguet [Reference Hladký, Hu and Piguet18].
Sparser graphs do not necessarily contain triangles, but most of them do if there are enough edges. To determine a cut-off point for the containment of a subgraph in the binomial random graph
![]() $G(n,p)$
, we define a threshold function. Before stating its definition, we remark that we say that a property
$G(n,p)$
, we define a threshold function. Before stating its definition, we remark that we say that a property
![]() $\mathcal{A}$
holds asymptotically almost surely (a.a.s.) in the random graph
$\mathcal{A}$
holds asymptotically almost surely (a.a.s.) in the random graph
![]() $G(n,p)$
if
$G(n,p)$
if
![]() $\lim _{n \to \infty }\mathbb{P}[G(n,p) \in \mathcal{A}]=1$
. Given a graph
$\lim _{n \to \infty }\mathbb{P}[G(n,p) \in \mathcal{A}]=1$
. Given a graph
![]() $H$
, the function
$H$
, the function
![]() $\hat{p} \;:\; \mathbb{N} \rightarrow [0,1]$
is called the threshold for the containment of
$\hat{p} \;:\; \mathbb{N} \rightarrow [0,1]$
is called the threshold for the containment of
![]() $H$
in
$H$
in
![]() $G(n,p)$
if a.a.s.
$G(n,p)$
if a.a.s.
![]() $H \subseteq G(n,p)$
for
$H \subseteq G(n,p)$
for
![]() $p = \omega (\hat{p})$
and a.a.s.
$p = \omega (\hat{p})$
and a.a.s.
![]() $H \not \subseteq G(n,p)$
for
$H \not \subseteq G(n,p)$
for
![]() $p=o(\hat{p})$
. Already in one of the early papers on random graphs by Erdős and Rényi [Reference Erdős and Rényi14] from
$p=o(\hat{p})$
. Already in one of the early papers on random graphs by Erdős and Rényi [Reference Erdős and Rényi14] from
![]() $1960$
, the threshold for a single triangle was determined as
$1960$
, the threshold for a single triangle was determined as
![]() $1/n$
. However, the problem for a triangle factor is much harder and was eventually solved by Johannson, Kahn, and Vu [Reference Johansson, Kahn and Vu20], in
$1/n$
. However, the problem for a triangle factor is much harder and was eventually solved by Johannson, Kahn, and Vu [Reference Johansson, Kahn and Vu20], in
![]() $2008$
, as part of a more general result, and the threshold was located at
$2008$
, as part of a more general result, and the threshold was located at
![]() $n^{-2/3} \log ^{1/3}n$
, with an even sharper transition than in our definition of threshold. When one requires
$n^{-2/3} \log ^{1/3}n$
, with an even sharper transition than in our definition of threshold. When one requires
![]() $\varepsilon n$
to
$\varepsilon n$
to
![]() $(1-\varepsilon )n$
pairwise vertex-disjoint triangles, the problem is easier and the threshold is
$(1-\varepsilon )n$
pairwise vertex-disjoint triangles, the problem is easier and the threshold is
![]() $n^{-2/3}$
as proved by Ruciński [Reference Ruciński29] in
$n^{-2/3}$
as proved by Ruciński [Reference Ruciński29] in
![]() $1992$
. Note that the the spanning version requires an extra
$1992$
. Note that the the spanning version requires an extra
![]() $\log ^{1/3}n$
, and this logarithmic term is essential to ensure that a.a.s. every vertex is contained in a triangle.
$\log ^{1/3}n$
, and this logarithmic term is essential to ensure that a.a.s. every vertex is contained in a triangle.
Bohman, Frieze, and Martin [Reference Bohman, Frieze and Martin7] combined the random graph model and the deterministic minimum-degree model by asking how many random edges one needs to add to a dense graph with small linear minimum degree, such that it contains a Hamilton cycle. More precisely, they introduced the model of randomly perturbed graphs as the union of an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G_\alpha$
with minimum degree at least
$G_\alpha$
with minimum degree at least
![]() $\alpha n$
and the random graph
$\alpha n$
and the random graph
![]() $G(n,p)$
. Given
$G(n,p)$
. Given
![]() $H$
and fixed
$H$
and fixed
![]() $\alpha$
, we are then interested in lower bounds on the edge-probability
$\alpha$
, we are then interested in lower bounds on the edge-probability
![]() $p$
such that a.a.s.
$p$
such that a.a.s.
![]() $G_\alpha \cup G(n,p)$
contains
$G_\alpha \cup G(n,p)$
contains
![]() $H$
for any
$H$
for any
![]() $G_\alpha$
. A lower bound
$G_\alpha$
. A lower bound
![]() $\hat{p}$
is optimal when in addition there exists a
$\hat{p}$
is optimal when in addition there exists a
![]() $G_\alpha$
for which a.a.s.
$G_\alpha$
for which a.a.s.
![]() $G_\alpha \cup G(n,p)$
does not contain
$G_\alpha \cup G(n,p)$
does not contain
![]() $H$
if
$H$
if
![]() $p=o(\hat{p})$
, in which case we call
$p=o(\hat{p})$
, in which case we call
![]() $\hat{p}$
the threshold for the containment of
$\hat{p}$
the threshold for the containment of
![]() $H$
in the randomly perturbed model. Note that this threshold
$H$
in the randomly perturbed model. Note that this threshold
![]() $\hat{p}$
only depends on
$\hat{p}$
only depends on
![]() $\alpha$
and
$\alpha$
and
![]() $H$
. In recent years, there has been a lot of work on embeddings of spanning graphs in randomly perturbed graphs. Most results in this model focus on the extreme cases with small
$H$
. In recent years, there has been a lot of work on embeddings of spanning graphs in randomly perturbed graphs. Most results in this model focus on the extreme cases with small
![]() $\alpha \gt 0$
[Reference Balogh, Treglown and Wagner4, Reference Bohman, Frieze, Krivelevich and Martin6, Reference Böttcher, Montgomery, Parczyk and Person8, Reference Joos and Kim21, Reference Krivelevich, Kwan and Sudakov23–Reference McDowell and Mycroft26] or small
$\alpha \gt 0$
[Reference Balogh, Treglown and Wagner4, Reference Bohman, Frieze, Krivelevich and Martin6, Reference Böttcher, Montgomery, Parczyk and Person8, Reference Joos and Kim21, Reference Krivelevich, Kwan and Sudakov23–Reference McDowell and Mycroft26] or small
![]() $p$
[Reference Antoniuk, Dudek, Reiher, Ruciński and Schacht2, Reference Bedenknecht, Han, Kohayakawa and Mota5, Reference Dudek, Reiher, Ruciński and Schacht13, Reference Nenadov and Trujić27]. More recently, Han, Morris, and Treglown [Reference Han, Morris and Treglown17] started a more thorough investigation of the intermediate regime. The goal is to determine the perturbed threshold for every
$p$
[Reference Antoniuk, Dudek, Reiher, Ruciński and Schacht2, Reference Bedenknecht, Han, Kohayakawa and Mota5, Reference Dudek, Reiher, Ruciński and Schacht13, Reference Nenadov and Trujić27]. More recently, Han, Morris, and Treglown [Reference Han, Morris and Treglown17] started a more thorough investigation of the intermediate regime. The goal is to determine the perturbed threshold for every
![]() $\alpha$
from
$\alpha$
from
![]() $\alpha =0$
, where we can rely only on
$\alpha =0$
, where we can rely only on
![]() $G(n,p)$
, to the
$G(n,p)$
, to the
![]() $\alpha$
where the structure already exists in
$\alpha$
where the structure already exists in
![]() $G_\alpha$
alone and
$G_\alpha$
alone and
![]() $p=0$
is sufficient.
$p=0$
is sufficient.
It is easy to see that with
![]() $0\lt \alpha \le 1/2$
,
$0\lt \alpha \le 1/2$
,
![]() $G_\alpha \cup G(n,p)$
a.a.s. contains a triangle when
$G_\alpha \cup G(n,p)$
a.a.s. contains a triangle when
![]() $p \ge C/n^2$
and
$p \ge C/n^2$
and
![]() $C$
is a sufficiently large constant depending on
$C$
is a sufficiently large constant depending on
![]() $\alpha$
. This is asymptotically optimal, as
$\alpha$
. This is asymptotically optimal, as
![]() $G(n,p)$
with
$G(n,p)$
with
![]() $p = o(n^2)$
a.a.s. is empty. Together with the cases for
$p = o(n^2)$
a.a.s. is empty. Together with the cases for
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\alpha \gt 1/2$
discussed above, this completes all the range of
$\alpha \gt 1/2$
discussed above, this completes all the range of
![]() $\alpha$
for the containment of a single triangle. For a triangle factor, we already know the threshold when
$\alpha$
for the containment of a single triangle. For a triangle factor, we already know the threshold when
![]() $\alpha =0$
from the random graph model, and when
$\alpha =0$
from the random graph model, and when
![]() $\alpha \ge 2/3$
we do not need random edges at all. For any
$\alpha \ge 2/3$
we do not need random edges at all. For any
![]() $\alpha \gt 0$
, Balogh, Treglown, and Wagner [Reference Balogh, Treglown and Wagner4] showed that
$\alpha \gt 0$
, Balogh, Treglown, and Wagner [Reference Balogh, Treglown and Wagner4] showed that
![]() $p \ge C n^{-2/3}$
is always sufficient (with
$p \ge C n^{-2/3}$
is always sufficient (with
![]() $C$
depending on
$C$
depending on
![]() $\alpha$
). This is asymptotically optimal in the case
$\alpha$
). This is asymptotically optimal in the case
![]() $0\lt \alpha \lt 1/3$
, as with
$0\lt \alpha \lt 1/3$
, as with
![]() $G_\alpha$
the complete bipartite graph with classes of size
$G_\alpha$
the complete bipartite graph with classes of size
![]() $\alpha n$
and
$\alpha n$
and
![]() $(1-\alpha n)$
, we need a linear number of triangles with all edges from the random graph, for which
$(1-\alpha n)$
, we need a linear number of triangles with all edges from the random graph, for which
![]() $n^{-2/3}$
is the threshold as discussed above. For
$n^{-2/3}$
is the threshold as discussed above. For
![]() $1/3 \lt \alpha \lt 2/3$
, Han, Morris, and Treglown [Reference Han, Morris and Treglown17] proved that then already
$1/3 \lt \alpha \lt 2/3$
, Han, Morris, and Treglown [Reference Han, Morris and Treglown17] proved that then already
![]() $p \ge C/n$
is enough for a triangle factor. Again this is asymptotically optimal as, when
$p \ge C/n$
is enough for a triangle factor. Again this is asymptotically optimal as, when
![]() $G_\alpha$
is the complete tripartite graph with classes of size
$G_\alpha$
is the complete tripartite graph with classes of size
![]() $\alpha n/2$
,
$\alpha n/2$
,
![]() $\alpha n/2$
and
$\alpha n/2$
and
![]() $(1-\alpha )n$
, we need a linear number of edges from
$(1-\alpha )n$
, we need a linear number of edges from
![]() $G(n,p)$
. Together, these results can be summarised as follows.
$G(n,p)$
. Together, these results can be summarised as follows.
Theorem 1.2 (Balogh, Treglown, and Wagner [Reference Balogh, Treglown and Wagner4] and Han, Morris, and Treglown [Reference Han, Morris and Treglown17]). Given any
![]() $\alpha \in (0,1/3) \cup (1/3,2/3)$
there exists
$\alpha \in (0,1/3) \cup (1/3,2/3)$
there exists
![]() $C\gt 0$
such that the following holds. For any
$C\gt 0$
such that the following holds. For any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G) \ge \alpha n$
, a.a.s. there is a triangle factor in
$\delta (G) \ge \alpha n$
, a.a.s. there is a triangle factor in
![]() $G \cup G(n,p)$
provided that
$G \cup G(n,p)$
provided that
![]() $p \ge C n^{-2/3}$
if
$p \ge C n^{-2/3}$
if
![]() $\alpha \in (0,1/3)$
and
$\alpha \in (0,1/3)$
and
![]() $p \ge C n^{-1}$
if
$p \ge C n^{-1}$
if
![]() $\alpha \in (1/3,2/3)$
.
$\alpha \in (1/3,2/3)$
.
In this paper, we close the remaining open case for the triangle factor, that is
![]() $\alpha = 1/3$
, for which we show that
$\alpha = 1/3$
, for which we show that
![]() $p \ge C \log n/n$
is sufficient.
$p \ge C \log n/n$
is sufficient.
Theorem 1.3.
There exists
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G) \ge n/3$
, we can a.a.s. find a triangle factor in
$\delta (G) \ge n/3$
, we can a.a.s. find a triangle factor in
![]() $G \cup G(n,p)$
, provided that
$G \cup G(n,p)$
, provided that
![]() $p\ge C \log n/n$
.
$p\ge C \log n/n$
.
To see that the bound on
![]() $p$
in Theorem 1.3 is asymptotically optimal consider the complete bipartite graph
$p$
in Theorem 1.3 is asymptotically optimal consider the complete bipartite graph
![]() $G=K_{n/3,2n/3}$
and denote the partition classes by
$G=K_{n/3,2n/3}$
and denote the partition classes by
![]() $A$
and
$A$
and
![]() $B$
with
$B$
with
![]() $|A|\lt |B|$
. By Markov’s inequality and with
$|A|\lt |B|$
. By Markov’s inequality and with
![]() $p \le \tfrac 12 \log n/n$
a.a.s. there are
$p \le \tfrac 12 \log n/n$
a.a.s. there are
![]() $O(\log ^4 n)$
triangles within
$O(\log ^4 n)$
triangles within
![]() $B$
and a.a.s. there is a polynomial number of vertices in the class
$B$
and a.a.s. there is a polynomial number of vertices in the class
![]() $B$
without any neighbours in
$B$
without any neighbours in
![]() $B$
[Reference Janson, Łuczak and Ruciński19, Theorem 6.36]. However, for a triangle factor to exist, for each triangle with at most one vertex in
$B$
[Reference Janson, Łuczak and Ruciński19, Theorem 6.36]. However, for a triangle factor to exist, for each triangle with at most one vertex in
![]() $B$
, there must be at least one triangle fully contained in
$B$
, there must be at least one triangle fully contained in
![]() $B$
. In conclusion, a.a.s.
$B$
. In conclusion, a.a.s.
![]() $G \cup G(n,p)$
does not contain a triangle factor, and the
$G \cup G(n,p)$
does not contain a triangle factor, and the
![]() $\log n$
-term is needed for local reasons similarly as discussed above for the triangle factor in
$\log n$
-term is needed for local reasons similarly as discussed above for the triangle factor in
![]() $G(n,p)$
.
$G(n,p)$
.
This result closes the problem of determining, given
![]() $\alpha \in [0,1]$
, the threshold for a triangle factor in
$\alpha \in [0,1]$
, the threshold for a triangle factor in
![]() $G_\alpha \cup G(n,p)$
and we refer to Table 1 for a summary. Note that the threshold is within a constant factor in the intervals
$G_\alpha \cup G(n,p)$
and we refer to Table 1 for a summary. Note that the threshold is within a constant factor in the intervals
![]() $(0,1/3)$
and
$(0,1/3)$
and
![]() $(1/3,2/3)$
, while it jumps at
$(1/3,2/3)$
, while it jumps at
![]() $\alpha =0$
,
$\alpha =0$
,
![]() $1/3$
, and
$1/3$
, and
![]() $2/3$
.
$2/3$
.
Table 1 Triangle factor containment in
![]() $G_\alpha \cup G(n,p)$
, where
$G_\alpha \cup G(n,p)$
, where
![]() $\delta (G_\alpha ) \ge \alpha n$
$\delta (G_\alpha ) \ge \alpha n$
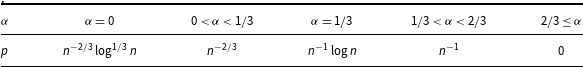
Theorem 1.3 is a special case of the following theorem, which is our main result. It answers the question which minimum degree condition is needed in the randomly perturbed graph model with
![]() $p= C\log n/n$
to enforce
$p= C\log n/n$
to enforce
![]() $k$
vertex-disjoint triangles for any
$k$
vertex-disjoint triangles for any
![]() $1\le k\le \lfloor n/3\rfloor$
.
$1\le k\le \lfloor n/3\rfloor$
.
Theorem 1.4 (Main result). There exists
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
we can a.a.s. find at least
$G$
we can a.a.s. find at least
![]() $\min \{ \delta (G), \lfloor n/3 \rfloor \}$
pairwise vertex-disjoint triangles in
$\min \{ \delta (G), \lfloor n/3 \rfloor \}$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
, provided that
$G \cup G(n,p)$
, provided that
![]() $p\ge C \log n/n$
.
$p\ge C \log n/n$
.
This is a perturbed version of the result by Dirac on vertex-disjoint triangles in dense graphs (Theorem 1.1). We are not aware of other results in the randomly perturbed graph model that consider large but not spanning structures.
Theorem 1.4 is basically optimal in terms of the number of triangles, because given
![]() $1 \le m \lt n/3$
, then
$1 \le m \lt n/3$
, then
![]() $G=K_{m,n-m}$
has minimum degree
$G=K_{m,n-m}$
has minimum degree
![]() $\delta (G)=m$
, and there can be at most
$\delta (G)=m$
, and there can be at most
![]() $m$
pairwise vertex-disjoint triangles using each at least one edge of
$m$
pairwise vertex-disjoint triangles using each at least one edge of
![]() $G$
, and at most
$G$
, and at most
![]() $O(\log ^4 n)$
additional triangles solely coming from
$O(\log ^4 n)$
additional triangles solely coming from
![]() $G(n,p)$
. The bound on
$G(n,p)$
. The bound on
![]() $p$
is asymptotically optimal as it is in Theorem 1.3, but we remark that when
$p$
is asymptotically optimal as it is in Theorem 1.3, but we remark that when
![]() $m$
is ‘significantly smaller’ than
$m$
is ‘significantly smaller’ than
![]() $n/3$
, then already
$n/3$
, then already
![]() $p \ge C/ n$
is sufficient to a.a.s. find
$p \ge C/ n$
is sufficient to a.a.s. find
![]() $m$
pairwise vertex-disjoint triangles in
$m$
pairwise vertex-disjoint triangles in
![]() $K_{m,n-m} \cup G(n,p)$
. We call
$K_{m,n-m} \cup G(n,p)$
. We call
![]() $K_{m,n-m}$
the extremal graph. See the concluding remarks (Section 9) for more details.
$K_{m,n-m}$
the extremal graph. See the concluding remarks (Section 9) for more details.
In addition, we prove a stability version (Theorem 2.2) of our main result, which allows us to work with edge probability only
![]() $p=C/n$
for graphs
$p=C/n$
for graphs
![]() $G$
that are not ‘close’Footnote
1
to the extremal graph.
$G$
that are not ‘close’Footnote
1
to the extremal graph.
We believe that the methods we introduce for proving our results are valuable for other questions concerning randomly perturbed graphs; we discuss some possible directions and open problems in Section 9. One important novel ingredient in our proofs is that we can find a triangle factor in a graph on three vertex sets
![]() $U, V, W$
of the same size, where
$U, V, W$
of the same size, where
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
are super-regular pairs and between
$(V,W)$
are super-regular pairs and between
![]() $U$
and
$U$
and
![]() $W$
we have random edges with probability
$W$
we have random edges with probability
![]() $p \ge C \log n/n$
(see Lemma 4.1).
$p \ge C \log n/n$
(see Lemma 4.1).
Organisation
The rest of this paper is organised as follows. In Section 2, we state our Stability Theorem (Theorem 2.2), one result (Theorem 2.3) that deals with the ‘extremal’ case of Theorem 1.4, and one result (Theorem 2.4) that deals with the case of small minimum degrees; we shall show that these three theorems together imply our main result (Theorem 1.4).
In Section 3, we then introduce some tools that we will use later. In Section 4, we outline the proofs of Theorems 2.2, 2.3, and 2.4 and we state the auxiliary lemmas we use in their proofs. In Section 5 we prove Theorem 2.3, in Section 6 we prove Theorem 2.2, and in Section 7 we prove Theorem 2.4. The auxiliary lemmas are proved in Section 8.
Finally, we give concluding remarks and pose some open questions in Section 9. A few supplementary proofs are moved to Appendix A.
Notation
For numbers
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
, we write
$c$
, we write
![]() $a = b \pm c$
for
$a = b \pm c$
for
![]() $b-c \le a \le b+c$
. Moreover, for non-negative
$b-c \le a \le b+c$
. Moreover, for non-negative
![]() $a$
,
$a$
,
![]() $b$
, we write
$b$
, we write
![]() $0\lt a \ll b$
, when we require
$0\lt a \ll b$
, when we require
![]() $a \le f(b)$
for some function
$a \le f(b)$
for some function
![]() $f \colon \mathbb{R}_{\gt 0} \mapsto \mathbb{R}_{\gt 0}$
. We will only use this to improve readability and in addition to the precise dependencies of the constants.
$f \colon \mathbb{R}_{\gt 0} \mapsto \mathbb{R}_{\gt 0}$
. We will only use this to improve readability and in addition to the precise dependencies of the constants.
We use standard graph theory notation. For a graph
![]() $G$
on vertex set
$G$
on vertex set
![]() $V$
and two disjoint sets
$V$
and two disjoint sets
![]() $A$
,
$A$
,
![]() $B \subseteq V$
, let
$B \subseteq V$
, let
![]() $G[A]$
be the subgraph of
$G[A]$
be the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $A$
,
$A$
,
![]() $G[A,B]$
be the bipartite subgraph of
$G[A,B]$
be the bipartite subgraph of
![]() $G$
induced by sets
$G$
induced by sets
![]() $A$
and
$A$
and
![]() $B$
,
$B$
,
![]() $e(A)$
be the number of edges with both endpoints in
$e(A)$
be the number of edges with both endpoints in
![]() $A$
and
$A$
and
![]() $e(A,B)$
be the number of edges with one endpoint in
$e(A,B)$
be the number of edges with one endpoint in
![]() $A$
and the other one in
$A$
and the other one in
![]() $B$
. We will also use standard Landau notation for
$B$
. We will also use standard Landau notation for
![]() $f,g \;:\; \mathbb{N} \rightarrow \mathbb{R}_{\gt 0} \;:\; f = o(g)$
if and only if
$f,g \;:\; \mathbb{N} \rightarrow \mathbb{R}_{\gt 0} \;:\; f = o(g)$
if and only if
![]() $\lim _{n \to \infty }f(n)/g(n)=0$
and
$\lim _{n \to \infty }f(n)/g(n)=0$
and
![]() $f = \omega (g)$
if and only if
$f = \omega (g)$
if and only if
![]() $g = o(f)$
.
$g = o(f)$
.
2. Stability version and proof of the main result
We already discussed how the probability
![]() $p \ge C \log n/n$
cannot be significantly lowered in Theorem 1.4. However, we are able to show that when the minimum degree of
$p \ge C \log n/n$
cannot be significantly lowered in Theorem 1.4. However, we are able to show that when the minimum degree of
![]() $G$
is linear in
$G$
is linear in
![]() $n$
, then with
$n$
, then with
![]() $m=\min \{\delta (G),n/3\}$
, the complete bipartite graph
$m=\min \{\delta (G),n/3\}$
, the complete bipartite graph
![]() $K_{m,n-m}$
is the unique extremal graph for Theorem 1.4, in the sense that if the graph
$K_{m,n-m}$
is the unique extremal graph for Theorem 1.4, in the sense that if the graph
![]() $G$
is not ‘close’ to
$G$
is not ‘close’ to
![]() $K_{m,n-m}$
then a.a.s.
$K_{m,n-m}$
then a.a.s.
![]() $G \cup G(n,p)$
contains
$G \cup G(n,p)$
contains
![]() $m$
pairwise vertex-disjoint triangles already at probability
$m$
pairwise vertex-disjoint triangles already at probability
![]() $p \ge C/n$
and we can even assume a slightly smaller minimum degree on
$p \ge C/n$
and we can even assume a slightly smaller minimum degree on
![]() $G$
. To formalise this, we introduce the following notion of stability for an
$G$
. To formalise this, we introduce the following notion of stability for an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
.
$G$
.
Definition 2.1 (
![]() $(\alpha,\beta )$
-stable). For
$(\alpha,\beta )$
-stable). For
![]() $0 \lt \beta \lt \alpha \lt 1/2$
, we say that an
$0 \lt \beta \lt \alpha \lt 1/2$
, we say that an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
is
$G$
is
![]() $(\alpha,\beta )$
-stable if there exists a partition of
$(\alpha,\beta )$
-stable if there exists a partition of
![]() $V(G)$
into two sets
$V(G)$
into two sets
![]() $A$
and
$A$
and
![]() $B$
of size
$B$
of size
![]() $|A|=(\alpha \pm \beta ) n$
and
$|A|=(\alpha \pm \beta ) n$
and
![]() $|B|=(1-\alpha \pm \beta ) n$
such that the minimum degree of the bipartite subgraph
$|B|=(1-\alpha \pm \beta ) n$
such that the minimum degree of the bipartite subgraph
![]() $G[A,B]$
of
$G[A,B]$
of
![]() $G$
induced by
$G$
induced by
![]() $A$
and
$A$
and
![]() $B$
is at least
$B$
is at least
![]() $\alpha n/4$
, all but at most
$\alpha n/4$
, all but at most
![]() $\beta n$
vertices from
$\beta n$
vertices from
![]() $A$
have degree at least
$A$
have degree at least
![]() $|B|-\beta n$
into
$|B|-\beta n$
into
![]() $B$
, all but at most
$B$
, all but at most
![]() $\beta n$
vertices from
$\beta n$
vertices from
![]() $B$
have degree at least
$B$
have degree at least
![]() $|A|-\beta n$
into
$|A|-\beta n$
into
![]() $A$
, and
$A$
, and
![]() $G[B]$
contains at most
$G[B]$
contains at most
![]() $\beta n^{2}$
edges.
$\beta n^{2}$
edges.
The stability condition with
![]() $\alpha =1/3$
says that the size of
$\alpha =1/3$
says that the size of
![]() $B$
is roughly double the size of
$B$
is roughly double the size of
![]() $A$
, there is a minimum degree condition between
$A$
, there is a minimum degree condition between
![]() $A$
and
$A$
and
![]() $B$
, in each part all but at most a few vertices see most of the other part, and the set
$B$
, in each part all but at most a few vertices see most of the other part, and the set
![]() $B$
is almost independent. Note that for
$B$
is almost independent. Note that for
![]() $0 \lt \alpha \le 1/3$
and
$0 \lt \alpha \le 1/3$
and
![]() $m=\alpha n$
an integer, the complete bipartite graph
$m=\alpha n$
an integer, the complete bipartite graph
![]() $K_{m,n-m}$
is
$K_{m,n-m}$
is
![]() $(\alpha,\beta )$
-stable with
$(\alpha,\beta )$
-stable with
![]() $\beta =0$
. We prove the following stability result in Section 6.
$\beta =0$
. We prove the following stability result in Section 6.
Theorem 2.2 (Stability Theorem). For
![]() $0 \lt \beta \lt 1/12$
there exist
$0 \lt \beta \lt 1/12$
there exist
![]() $\gamma \gt 0$
and
$\gamma \gt 0$
and
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $\alpha$
with
$\alpha$
with
![]() $4 \beta \le \alpha \le 1/3$
the following holds. Let
$4 \beta \le \alpha \le 1/3$
the following holds. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta (G) \ge \left (\alpha - \gamma \right ) n$
that is not
$\delta (G) \ge \left (\alpha - \gamma \right ) n$
that is not
![]() $(\alpha,\beta )$
-stable. With
$(\alpha,\beta )$
-stable. With
![]() $p\ge C/n$
a.a.s. the perturbed graph
$p\ge C/n$
a.a.s. the perturbed graph
![]() $G \cup G(n,p)$
contains at least
$G \cup G(n,p)$
contains at least
![]() $ \min \{ \alpha n, \lfloor n/3 \rfloor \}$
pairwise vertex-disjoint triangles.
$ \min \{ \alpha n, \lfloor n/3 \rfloor \}$
pairwise vertex-disjoint triangles.
The result is best possible as
![]() $G$
can be bipartite and have no triangles, in which case we need at least a linear number of edges from the random graph to find a linear number of pairwise vertex-disjoint triangles in
$G$
can be bipartite and have no triangles, in which case we need at least a linear number of edges from the random graph to find a linear number of pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
. On the other hand, the logarithmic factor is needed for the extremal graph. When the graph
$G \cup G(n,p)$
. On the other hand, the logarithmic factor is needed for the extremal graph. When the graph
![]() $G$
is
$G$
is
![]() $(\alpha, \beta )$
-stable for a small enough
$(\alpha, \beta )$
-stable for a small enough
![]() $\beta \gt 0$
, then we prove the following in Section 5.
$\beta \gt 0$
, then we prove the following in Section 5.
Theorem 2.3 (Extremal Theorem). For
![]() $0 \lt \alpha _0 \le 1/3$
there exist
$0 \lt \alpha _0 \le 1/3$
there exist
![]() $\beta,\gamma \gt 0$
and
$\beta,\gamma \gt 0$
and
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $\alpha$
with
$\alpha$
with
![]() $\alpha _0 \le \alpha \le 1/3$
the following holds. Let
$\alpha _0 \le \alpha \le 1/3$
the following holds. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta (G) \ge \left ( \alpha -\gamma \right ) n$
that is
$\delta (G) \ge \left ( \alpha -\gamma \right ) n$
that is
![]() $(\alpha,\beta )$
-stable. With
$(\alpha,\beta )$
-stable. With
![]() $p\ge C \log n/n$
a.a.s. the perturbed graph
$p\ge C \log n/n$
a.a.s. the perturbed graph
![]() $G \cup G(n,p)$
contains at least
$G \cup G(n,p)$
contains at least
![]() $\min \{ \delta (G), \lfloor \alpha n \rfloor \}$
pairwise vertex-disjoint triangles.
$\min \{ \delta (G), \lfloor \alpha n \rfloor \}$
pairwise vertex-disjoint triangles.
Indeed our argument will give slightly more. If
![]() $G$
is
$G$
is
![]() $(\alpha,\beta )$
-stable and
$(\alpha,\beta )$
-stable and
![]() $|A| \ge \alpha n$
, then we can a.a.s. find
$|A| \ge \alpha n$
, then we can a.a.s. find
![]() $\lceil \alpha n \rceil$
if
$\lceil \alpha n \rceil$
if
![]() $\alpha \lt 1/3$
and
$\alpha \lt 1/3$
and
![]() $\lfloor n/3 \rfloor$
if
$\lfloor n/3 \rfloor$
if
![]() $\alpha =1/3$
pairwise vertex-disjoint triangles in
$\alpha =1/3$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
(even when the minimum degree in
$G \cup G(n,p)$
(even when the minimum degree in
![]() $G$
is smaller than
$G$
is smaller than
![]() $\alpha n$
). Also, although as discussed above the
$\alpha n$
). Also, although as discussed above the
![]() $\log n$
-factor cannot be avoided in general, when
$\log n$
-factor cannot be avoided in general, when
![]() $|A|-\alpha n$
is linear in
$|A|-\alpha n$
is linear in
![]() $n$
our proof does not need such a
$n$
our proof does not need such a
![]() $\log n$
-factor.
$\log n$
-factor.
The proofs of Theorem 2.2 and 2.3 use regularity. When the minimum degree gets smaller, we can avoid the transition to sparse regularity and prove the following in Section 7 with a more elementary argument.
Theorem 2.4 (Sublinear Theorem). There exists
![]() $C\gt 0$
such that the following holds for any
$C\gt 0$
such that the following holds for any
![]() $1 \le m \le n/256$
and any
$1 \le m \le n/256$
and any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
of minimum degree
$G$
of minimum degree
![]() $\delta (G) \ge m$
. With
$\delta (G) \ge m$
. With
![]() $p \ge C \log n/n$
a.a.s. the perturbed graph
$p \ge C \log n/n$
a.a.s. the perturbed graph
![]() $G \cup G(n,p)$
contains at least
$G \cup G(n,p)$
contains at least
![]() $m$
pairwise vertex-disjoint triangles.
$m$
pairwise vertex-disjoint triangles.
Theorem 1.4 easily follows from Theorems 2.2, 2.3, and 2.4.
Proof of Theorem 1.4.Let
![]() $\beta _{2.3}, \gamma _{2.3}\gt 0$
and
$\beta _{2.3}, \gamma _{2.3}\gt 0$
and
![]() $C_{2.3}$
be given by Theorem 2.3 on input
$C_{2.3}$
be given by Theorem 2.3 on input
![]() $\alpha _0=1/256$
. Then let
$\alpha _0=1/256$
. Then let
![]() $\gamma _{2.2}\gt 0$
and
$\gamma _{2.2}\gt 0$
and
![]() $C_{2.2}$
be given by Theorem 2.2 on input
$C_{2.2}$
be given by Theorem 2.2 on input
![]() $\beta = \min \{ \alpha _0/4, \beta _{2.3} \}$
. Moreover, let
$\beta = \min \{ \alpha _0/4, \beta _{2.3} \}$
. Moreover, let
![]() $C_{2.4}$
be given by Theorem 2.4. Define
$C_{2.4}$
be given by Theorem 2.4. Define
![]() $C = \max \{ C_{2.3},C_{2.4} \}$
and
$C = \max \{ C_{2.3},C_{2.4} \}$
and
![]() $\gamma =\min \{ \gamma _{2.3},\gamma _{2.2} \}$
.
$\gamma =\min \{ \gamma _{2.3},\gamma _{2.2} \}$
.
Let
![]() $G$
be any
$G$
be any
![]() $n$
-vertex graph and
$n$
-vertex graph and
![]() $p \ge C \log n/n$
, and define
$p \ge C \log n/n$
, and define
![]() $m= \min \{ \delta (G), \lfloor n/3 \rfloor \}$
. If
$m= \min \{ \delta (G), \lfloor n/3 \rfloor \}$
. If
![]() $m \le n/256$
, then we get from Theorem 2.4 that a.a.s.
$m \le n/256$
, then we get from Theorem 2.4 that a.a.s.
![]() $G \cup G(n,p)$
contains at least
$G \cup G(n,p)$
contains at least
![]() $m$
pairwise vertex-disjoint triangles, as
$m$
pairwise vertex-disjoint triangles, as
![]() $C \ge C_{2.4}$
. Otherwise,
$C \ge C_{2.4}$
. Otherwise,
![]() $m \gt n/256$
and we can choose
$m \gt n/256$
and we can choose
![]() $\alpha \in (\alpha _0,1/3]$
such that
$\alpha \in (\alpha _0,1/3]$
such that
![]() $(\alpha -\gamma )n \le m \le \alpha n$
. If
$(\alpha -\gamma )n \le m \le \alpha n$
. If
![]() $G$
is
$G$
is
![]() $(\alpha,\beta )$
-stable, then
$(\alpha,\beta )$
-stable, then
![]() $G$
is also
$G$
is also
![]() $(\alpha,\beta _{2.3})$
-stable and, by Theorem 2.3, there are a.a.s. at least
$(\alpha,\beta _{2.3})$
-stable and, by Theorem 2.3, there are a.a.s. at least
![]() $\min \{ \delta (G),\lfloor \alpha n\rfloor \} \ge m$
pairwise vertex-disjoint triangles in
$\min \{ \delta (G),\lfloor \alpha n\rfloor \} \ge m$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
, as
$G \cup G(n,p)$
, as
![]() $\alpha _0 \lt \alpha \le 1/3$
and
$\alpha _0 \lt \alpha \le 1/3$
and
![]() $C \ge C_{2.3}$
. Otherwise,
$C \ge C_{2.3}$
. Otherwise,
![]() $G$
is not
$G$
is not
![]() $(\alpha,\beta )$
-stable and, by Theorem 2.2, a.a.s.
$(\alpha,\beta )$
-stable and, by Theorem 2.2, a.a.s.
![]() $G \cup G(n,p)$
contains at least
$G \cup G(n,p)$
contains at least
![]() $ \min \{ \alpha n, \lfloor n/3 \rfloor \} \ge m$
pairwise vertex-disjoint triangles, as
$ \min \{ \alpha n, \lfloor n/3 \rfloor \} \ge m$
pairwise vertex-disjoint triangles, as
![]() $p = \omega (1/n)$
.
$p = \omega (1/n)$
.
3. Tools
We will repeatedly use the following concentration inequality due to Chernoff (see e.g. [Reference Janson, Łuczak and Ruciński19, Corollaries 2.3 and 2.4]).
Lemma 3.1 (Chernoff’s inequality). Let
![]() $X$
be the sum of independent binomial random variables, then for any
$X$
be the sum of independent binomial random variables, then for any
![]() $\delta \in (0,1)$
we have
$\delta \in (0,1)$
we have
Moreover, for any
![]() $k \ge 7\, \mathbb{E}[X]$
, we have
$k \ge 7\, \mathbb{E}[X]$
, we have
![]() $\mathbb{P}[X \gt k] \le \exp (-k)$
.
$\mathbb{P}[X \gt k] \le \exp (-k)$
.
The following lemma allows us to find specific triangles in a dense graph with additional random edges. The proof is a standard application of Janson’s inequality (see e.g. [Reference Janson, Łuczak and Ruciński19, Theorem 2.18]), and it is included in Appendix A.
Lemma 3.2.
For any
![]() $d\gt 0$
there exists
$d\gt 0$
there exists
![]() $C\gt 0$
such that the following holds. Let
$C\gt 0$
such that the following holds. Let
![]() $U,V,W$
be three sets of vertices of size
$U,V,W$
be three sets of vertices of size
![]() $n$
,
$n$
,
![]() $G$
be a bipartite graph on
$G$
be a bipartite graph on
![]() $(U,W)$
with
$(U,W)$
with
![]() $e(G) \ge d n^2$
,
$e(G) \ge d n^2$
,
![]() $p \gt C/n$
and
$p \gt C/n$
and
![]() $G(U \cup W,V,p)$
be the random bipartite graph. Then with probability at least
$G(U \cup W,V,p)$
be the random bipartite graph. Then with probability at least
![]() $1-2^{-4n/d}$
there is a triangle in
$1-2^{-4n/d}$
there is a triangle in
![]() $G \cup G(U \cup W,V,p)$
with one vertex in each of
$G \cup G(U \cup W,V,p)$
with one vertex in each of
![]() $U,V,W$
.
$U,V,W$
.
We will use Szemerédi’s Regularity Lemma [Reference Szemerédi30] and some of its consequences. Before stating it, we introduce the relevant terminology. The density of a pair
![]() $(A,B)$
of disjoint sets of vertices is defined by
$(A,B)$
of disjoint sets of vertices is defined by
and the pair
![]() $(A,B)$
is called
$(A,B)$
is called
![]() $\varepsilon$
-regular, if for all sets
$\varepsilon$
-regular, if for all sets
![]() $X \subseteq A$
and
$X \subseteq A$
and
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|X| \ge \varepsilon |A|$
and
$|X| \ge \varepsilon |A|$
and
![]() $|Y| \ge \varepsilon |B|$
we have
$|Y| \ge \varepsilon |B|$
we have
![]() $|d(A,B)-d(X,Y)| \le \varepsilon$
. Without further mentioning it, we will repeatedly use that when
$|d(A,B)-d(X,Y)| \le \varepsilon$
. Without further mentioning it, we will repeatedly use that when
![]() $\varepsilon \lt 1/2$
any
$\varepsilon \lt 1/2$
any
![]() $A' \subseteq A$
with
$A' \subseteq A$
with
![]() $|A'| \ge |A|/2$
and
$|A'| \ge |A|/2$
and
![]() $B' \subseteq B$
with
$B' \subseteq B$
with
![]() $|B'| \ge |B|/2$
give a
$|B'| \ge |B|/2$
give a
![]() $2\varepsilon$
-regular pair
$2\varepsilon$
-regular pair
![]() $(A',B')$
with density at least
$(A',B')$
with density at least
![]() $d(A,B)-\varepsilon$
.
$d(A,B)-\varepsilon$
.
We will also use the following well-known result that follows from the definition.
Lemma 3.3 (Minimum Degree Lemma). Let
![]() $(A,B)$
be an
$(A,B)$
be an
![]() $\varepsilon$
-regular pair with
$\varepsilon$
-regular pair with
![]() $d(A,B)=d$
. Then for every
$d(A,B)=d$
. Then for every
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|Y| \ge \varepsilon |B|$
, the number of vertices from
$|Y| \ge \varepsilon |B|$
, the number of vertices from
![]() $A$
with degree into
$A$
with degree into
![]() $Y$
less than
$Y$
less than
![]() $(d-\varepsilon )|Y|$
is at most
$(d-\varepsilon )|Y|$
is at most
![]() $\varepsilon |A|$
.
$\varepsilon |A|$
.
With
![]() $d \in [0,1)$
a pair
$d \in [0,1)$
a pair
![]() $(A,B)$
is called
$(A,B)$
is called
![]() $(\varepsilon,d)$
-super-regular, if for all sets
$(\varepsilon,d)$
-super-regular, if for all sets
![]() $X \subseteq A$
and
$X \subseteq A$
and
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|X| \ge \varepsilon |A|$
and
$|X| \ge \varepsilon |A|$
and
![]() $|Y| \ge \varepsilon |B|$
we have
$|Y| \ge \varepsilon |B|$
we have
![]() $d(X,Y) \ge d$
and
$d(X,Y) \ge d$
and
![]() $\deg (a) \ge d|B|$
for all
$\deg (a) \ge d|B|$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $\deg (b) \ge d|A|$
for all
$\deg (b) \ge d|A|$
for all
![]() $b \in B$
. It is easy to prove with Hall’s Theorem that a super-regular pair with parts of the same size contains a perfect matching.
$b \in B$
. It is easy to prove with Hall’s Theorem that a super-regular pair with parts of the same size contains a perfect matching.
Lemma 3.4.
For any
![]() $d\gt 0$
there exists
$d\gt 0$
there exists
![]() $\varepsilon \gt 0$
such that any
$\varepsilon \gt 0$
such that any
![]() $(\varepsilon,d)$
-super-regular pair
$(\varepsilon,d)$
-super-regular pair
![]() $(U,V)$
with
$(U,V)$
with
![]() $|U|=|V|$
contains a perfect matching.
$|U|=|V|$
contains a perfect matching.
We will use the following well-known degree form of the regularity lemma that can be derived from the original version [Reference Szemerédi30].
Lemma 3.5 ([Reference Komlós and Simonovits22]). For every
![]() $\varepsilon \gt 0$
and integer
$\varepsilon \gt 0$
and integer
![]() $t_0$
there exists an integer
$t_0$
there exists an integer
![]() $T\gt t_0$
such that for any graph
$T\gt t_0$
such that for any graph
![]() $G$
on at least
$G$
on at least
![]() $T$
vertices and
$T$
vertices and
![]() $d \in [0,1]$
there is a partition of
$d \in [0,1]$
there is a partition of
![]() $V(G)$
into
$V(G)$
into
![]() $t_0 \lt t+1 \le T$
sets
$t_0 \lt t+1 \le T$
sets
![]() $V_0,\dots,V_{t}$
and a subgraph
$V_0,\dots,V_{t}$
and a subgraph
![]() $G'$
of
$G'$
of
![]() $G$
such that
$G$
such that
-
(P1)
 $|V_i| = |V_j|$
for all
$|V_i| = |V_j|$
for all
 $1 \le i,j \le t$
and
$1 \le i,j \le t$
and
 $|V_0|\le \varepsilon |V(G)|$
,
$|V_0|\le \varepsilon |V(G)|$
, -
(P2)
 $\deg _{G'}(v) \ge \deg _G(v) - (d+\varepsilon ) |V(G)|$
for all
$\deg _{G'}(v) \ge \deg _G(v) - (d+\varepsilon ) |V(G)|$
for all
 $v \in V(G)$
,
$v \in V(G)$
, -
(P3) the set
 $V_i$
is independent in
$V_i$
is independent in
 $G'$
for all
$G'$
for all
 $1 \le i \le t$
,
$1 \le i \le t$
, -
(P4) for all
 $1 \le i \lt j \le t$
, the pair
$1 \le i \lt j \le t$
, the pair
 $(V_i,V_j)$
is
$(V_i,V_j)$
is
 $\varepsilon$
-regular in
$\varepsilon$
-regular in
 $G'$
and has density either
$G'$
and has density either
 $0$
or at least
$0$
or at least
 $d$
.
$d$
.
The sets
![]() $V_1, \dots, V_t$
are also called clusters, and we refer to
$V_1, \dots, V_t$
are also called clusters, and we refer to
![]() $V_0$
as the set of exceptional vertices. We call a partition
$V_0$
as the set of exceptional vertices. We call a partition
![]() $V_0, \dots, V_t$
, which satisfies (P1)–(P4), a
$V_0, \dots, V_t$
, which satisfies (P1)–(P4), a
![]() $(\varepsilon,d)$
-regular partition of
$(\varepsilon,d)$
-regular partition of
![]() $G$
. Given this partition, we define the
$G$
. Given this partition, we define the
![]() $(\varepsilon,d)$
-reduced graph
$(\varepsilon,d)$
-reduced graph
![]() $R$
for
$R$
for
![]() $G$
, that is the graph on the vertex set
$G$
, that is the graph on the vertex set
![]() $[t]$
, where
$[t]$
, where
![]() $ij$
is an edge if and only if
$ij$
is an edge if and only if
![]() $(V_i,V_j)$
is an
$(V_i,V_j)$
is an
![]() $\varepsilon$
-regular pair in
$\varepsilon$
-regular pair in
![]() $G'$
and has density at least
$G'$
and has density at least
![]() $d$
.
$d$
.
We will also use the following result on perfect matchings in random subgraphs of bipartite graphs with large minimum degree. For any given graph
![]() $G$
, we denote by
$G$
, we denote by
![]() $G_p$
the random graph model, where we keep each edge of
$G_p$
the random graph model, where we keep each edge of
![]() $G$
with probability
$G$
with probability
![]() $p$
, independently from all other choices.
$p$
, independently from all other choices.
Lemma 3.6.
For any
![]() $\varepsilon \gt 0$
there exists
$\varepsilon \gt 0$
there exists
![]() $C\gt 0$
such that the following holds for any bipartite graph
$C\gt 0$
such that the following holds for any bipartite graph
![]() $G$
with partition classes
$G$
with partition classes
![]() $|U|=|W|=n$
and minimum degree
$|U|=|W|=n$
and minimum degree
![]() $\delta (G)\ge (1/2+\varepsilon ) n$
. With
$\delta (G)\ge (1/2+\varepsilon ) n$
. With
![]() $p\ge C \log n/n$
there is a.a.s. a perfect matching in
$p\ge C \log n/n$
there is a.a.s. a perfect matching in
![]() $G_p$
.
$G_p$
.
The proof is standard and closely follows the proof for the perfect matching threshold in the random bipartite graph
![]() $G(n,n,p)$
(see [Reference Janson, Łuczak and Ruciński19, Theorem 4.1]). For completeness, we include it in Appendix A.
$G(n,n,p)$
(see [Reference Janson, Łuczak and Ruciński19, Theorem 4.1]). For completeness, we include it in Appendix A.
4. Proof overview and main Lemmas
In this section, we sketch the ideas behind our proof of Theorem 2.2, 2.3, and 2.4, and we give the statements of the lemmas we use. For simplicity, when outlining the proof of Theorem 2.2 and 2.3, we assume
![]() $\alpha =1/3$
,
$\alpha =1/3$
,
![]() $n$
is a multiple of
$n$
is a multiple of
![]() $3$
, and
$3$
, and
![]() $G$
is an
$G$
is an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta (G) \ge n/3$
, in which case both theorems give a triangle factor in
$\delta (G) \ge n/3$
, in which case both theorems give a triangle factor in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
4.1 Extremal case
Assume that
![]() $G$
is
$G$
is
![]() $(1/3,\beta )$
-stable and let
$(1/3,\beta )$
-stable and let
![]() $p\ge C \log n/n$
. The definition of stability (Definition 2.1) gives a partition of
$p\ge C \log n/n$
. The definition of stability (Definition 2.1) gives a partition of
![]() $V(G)$
into
$V(G)$
into
![]() $A \cup B$
where the size of
$A \cup B$
where the size of
![]() $B$
is roughly the double of the size of
$B$
is roughly the double of the size of
![]() $A$
, there is a minimum degree condition between
$A$
, there is a minimum degree condition between
![]() $A$
and
$A$
and
![]() $B$
, and in each part all but at most a few vertices see all but at most few a vertices of the other part. Our proof will follow three steps. Firstly, we find a collection of triangles
$B$
, and in each part all but at most a few vertices see all but at most few a vertices of the other part. Our proof will follow three steps. Firstly, we find a collection of triangles
![]() $\mathcal{T}_1$
, such that after removing the triangles of
$\mathcal{T}_1$
, such that after removing the triangles of
![]() $\mathcal{T}_1$
, we are left with two sets
$\mathcal{T}_1$
, we are left with two sets
![]() $A_1=A \setminus V(\mathcal{T}_1)$
and
$A_1=A \setminus V(\mathcal{T}_1)$
and
![]() $B_1=B \setminus V(\mathcal{T}_1)$
with
$B_1=B \setminus V(\mathcal{T}_1)$
with
![]() $|B_1| = 2|A_1|$
. The way we find these triangles depend on the sizes of
$|B_1| = 2|A_1|$
. The way we find these triangles depend on the sizes of
![]() $A$
and
$A$
and
![]() $B$
, and we will use two different approaches when
$B$
, and we will use two different approaches when
![]() $|B| \gt 2n/3$
and
$|B| \gt 2n/3$
and
![]() $|B| \le 2n/3$
. In particular, when
$|B| \le 2n/3$
. In particular, when
![]() $|B| \gt 2n/3$
, we need to find some triangles entirely within
$|B| \gt 2n/3$
, we need to find some triangles entirely within
![]() $B$
, just using the minimum degree
$B$
, just using the minimum degree
![]() $n/3-|A|$
and random edges. For that we will use Theorem 2.4.
$n/3-|A|$
and random edges. For that we will use Theorem 2.4.
Our second step is to cover the vertices in
![]() $A_1$
and
$A_1$
and
![]() $B_1$
that do not have a high degree to the other part; this will give two collections of triangles
$B_1$
that do not have a high degree to the other part; this will give two collections of triangles
![]() $\mathcal{T}_2$
and
$\mathcal{T}_2$
and
![]() $\mathcal{T}_3$
. Each such triangle has one vertex in
$\mathcal{T}_3$
. Each such triangle has one vertex in
![]() $A_1$
and two vertices in
$A_1$
and two vertices in
![]() $B_1$
so that we still have
$B_1$
so that we still have
![]() $|B_2| = 2 |A_2|$
, where
$|B_2| = 2 |A_2|$
, where
![]() $A_2=A_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
and
$A_2=A_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
and
![]() $B_2=B_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
. Moreover, at this point, each vertex sees all but at most a few vertices of the other part. We are now ready for the last step. We split
$B_2=B_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
. Moreover, at this point, each vertex sees all but at most a few vertices of the other part. We are now ready for the last step. We split
![]() $B_2$
arbitrarily into two subsets
$B_2$
arbitrarily into two subsets
![]() $B'_{\!\!1}$
and
$B'_{\!\!1}$
and
![]() ${B''}_{\!\!\!2}$
of equal size and we obtain that
${B''}_{\!\!\!2}$
of equal size and we obtain that
![]() $(B'_{\!\!1}$
,
$(B'_{\!\!1}$
,
![]() $A_2$
,
$A_2$
,
![]() ${B''}_{\!\!\!2})$
is a super-regular cherry, i.e. both
${B''}_{\!\!\!2})$
is a super-regular cherry, i.e. both
![]() $(B'_{\!\!1},A_2)$
and
$(B'_{\!\!1},A_2)$
and
![]() $({B''}_{\!\!\!2},A_2)$
are super-regular pairs. We want to find a triangle factor covering the cherry, with the help of random edges between
$({B''}_{\!\!\!2},A_2)$
are super-regular pairs. We want to find a triangle factor covering the cherry, with the help of random edges between
![]() $B'_{\!\!1}$
and
$B'_{\!\!1}$
and
![]() ${B''}_{\!\!\!2}$
. The next lemma, which encapsulates the main idea of our paper, takes care of this and will be proved in Section 8.
${B''}_{\!\!\!2}$
. The next lemma, which encapsulates the main idea of our paper, takes care of this and will be proved in Section 8.
Lemma 4.1.
For any
![]() $0\lt d\lt 1$
there exist
$0\lt d\lt 1$
there exist
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $C\gt 0$
such that the following holds. Let
$C\gt 0$
such that the following holds. Let
![]() $U,V,W$
be sets of size
$U,V,W$
be sets of size
![]() $n$
, let
$n$
, let
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
be
$(V,W)$
be
![]() $(\varepsilon,d)$
-super-regular pairs and let
$(\varepsilon,d)$
-super-regular pairs and let
![]() $G(U,W,p)$
be a random bipartite graph with
$G(U,W,p)$
be a random bipartite graph with
![]() $p\ge C \log n/n$
. Then a.a.s. there exists a triangle factor.
$p\ge C \log n/n$
. Then a.a.s. there exists a triangle factor.
Thus, we are able to cover the cherry with a triangle factor
![]() $\mathcal{T}_4$
, and we conclude observing that the collection of triangles
$\mathcal{T}_4$
, and we conclude observing that the collection of triangles
![]() $\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3 \cup \mathcal{T}_4$
gives a triangle factor in
$\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3 \cup \mathcal{T}_4$
gives a triangle factor in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
4.2 Non-extremal case
Before giving an overview of Theorem 2.2, it is worth to make some comments about Lemma 4.1. We point out that the probability
![]() $p$
cannot be significantly lowered. Indeed, a triangle factor in the setting of Lemma 4.1 gives a perfect matching in the random bipartite graph on vertex set
$p$
cannot be significantly lowered. Indeed, a triangle factor in the setting of Lemma 4.1 gives a perfect matching in the random bipartite graph on vertex set
![]() $U \cup W$
and this is a.a.s. not possible with
$U \cup W$
and this is a.a.s. not possible with
![]() $p\le \frac{1}{2} \log n/n$
[Reference Janson, Łuczak and Ruciński19, Theorem 4.1]. However, we would like to be able to find a triangle factor in a super-regular cherry with the help of the random edges also in the proof of Theorem 2.2, where we claimed that when the graph
$p\le \frac{1}{2} \log n/n$
[Reference Janson, Łuczak and Ruciński19, Theorem 4.1]. However, we would like to be able to find a triangle factor in a super-regular cherry with the help of the random edges also in the proof of Theorem 2.2, where we claimed that when the graph
![]() $G$
is not
$G$
is not
![]() $(1/3,\beta )$
-stable, already
$(1/3,\beta )$
-stable, already
![]() $p \ge C/n$
is sufficient. For that we will use the following variation of Lemma 4.1, where the improvement on the probability comes from the assumption that the super-regular cherry
$p \ge C/n$
is sufficient. For that we will use the following variation of Lemma 4.1, where the improvement on the probability comes from the assumption that the super-regular cherry
![]() $U,V,W$
is a bit unbalanced as the sizes of
$U,V,W$
is a bit unbalanced as the sizes of
![]() $U$
and
$U$
and
![]() $W$
are smaller than the size of
$W$
are smaller than the size of
![]() $V$
, and thus the random bipartite graph on vertex set
$V$
, and thus the random bipartite graph on vertex set
![]() $U \cup W$
will be used to build a large matching covering all but a small linear fraction of vertices, which is possible already with
$U \cup W$
will be used to build a large matching covering all but a small linear fraction of vertices, which is possible already with
![]() $p \ge C/n$
. Note that here we need to use random edges within
$p \ge C/n$
. Note that here we need to use random edges within
![]() $V$
.
$V$
.
Lemma 4.2.
For any
![]() $0\lt \delta '\le d\lt 1$
there exist
$0\lt \delta '\le d\lt 1$
there exist
![]() $\delta _0,\delta,\varepsilon$
with
$\delta _0,\delta,\varepsilon$
with
![]() $\delta '\ge \delta _0\gt \delta \gt \varepsilon \gt 0$
and
$\delta '\ge \delta _0\gt \delta \gt \varepsilon \gt 0$
and
![]() $C\gt 0$
such that the following holds. Let
$C\gt 0$
such that the following holds. Let
![]() $U,V,W$
be sets of size
$U,V,W$
be sets of size
![]() $|V|=n$
and
$|V|=n$
and
![]() $(1-\delta _0) n \le |U|=|W| \le (1-\delta )n$
where
$(1-\delta _0) n \le |U|=|W| \le (1-\delta )n$
where
![]() $|V|+|U|+|W| \equiv 0 \pmod 3$
. Further, let
$|V|+|U|+|W| \equiv 0 \pmod 3$
. Further, let
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
be
$(V,W)$
be
![]() $(\varepsilon,d)$
-super-regular pairs and let
$(\varepsilon,d)$
-super-regular pairs and let
![]() $G(V,p)$
,
$G(V,p)$
,
![]() $G(U,W,p)$
be random graphs with
$G(U,W,p)$
be random graphs with
![]() $p\ge C/n$
. Then a.a.s. there exists a triangle factor.
$p\ge C/n$
. Then a.a.s. there exists a triangle factor.
From Lemma 4.2, we also derive the following result about the existence of a triangle factor in a super-regular pair edge, again with the help of the random edges. Lemmas 4.2, and 4.3 will be proved in Section 8.
Lemma 4.3.
For any
![]() $0\lt d\lt 1$
there exist
$0\lt d\lt 1$
there exist
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $C\gt 0$
such the following holds for sets
$C\gt 0$
such the following holds for sets
![]() $U,V$
of size
$U,V$
of size
![]() $|V|=n$
and
$|V|=n$
and
![]() $3n/4 \le |U| \le n$
where
$3n/4 \le |U| \le n$
where
![]() $|V|+|U| \equiv 0 \pmod 3$
. If
$|V|+|U| \equiv 0 \pmod 3$
. If
![]() $(U,V)$
is an
$(U,V)$
is an
![]() $(\varepsilon,d)$
-super-regular pair and
$(\varepsilon,d)$
-super-regular pair and
![]() $G(U,p)$
and
$G(U,p)$
and
![]() $G(V,p)$
are random graphs with
$G(V,p)$
are random graphs with
![]() $p\ge C/n$
, then a.a.s. there exists a triangle factor.
$p\ge C/n$
, then a.a.s. there exists a triangle factor.
Now we turn to the overview of the proof for Theorem 2.2. Assume that
![]() $G$
is not
$G$
is not
![]() $(1/3,\beta )$
-stable and let
$(1/3,\beta )$
-stable and let
![]() $p\ge C/n$
. We apply the regularity lemma to
$p\ge C/n$
. We apply the regularity lemma to
![]() $G$
and obtain the reduced graph
$G$
and obtain the reduced graph
![]() $R$
. By adjusting an argument of the fourth author with Balogh and Mousset [Reference Balogh, Mousset and Skokan3], we can prove the following stability result.
$R$
. By adjusting an argument of the fourth author with Balogh and Mousset [Reference Balogh, Mousset and Skokan3], we can prove the following stability result.
Lemma 4.4.
For any
![]() $0\lt \beta \lt 1/12$
there exists
$0\lt \beta \lt 1/12$
there exists
![]() $d\gt 0$
such that the following holds for any
$d\gt 0$
such that the following holds for any
![]() $0\lt \varepsilon \lt d/4$
,
$0\lt \varepsilon \lt d/4$
,
![]() $4 \beta \le \alpha \le 1/3$
, and
$4 \beta \le \alpha \le 1/3$
, and
![]() $t \ge 10/d$
. Let
$t \ge 10/d$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta (G) \ge (\alpha -d/2)n$
that is not
$\delta (G) \ge (\alpha -d/2)n$
that is not
![]() $(\alpha,\beta )$
-stable and let
$(\alpha,\beta )$
-stable and let
![]() $R$
be the
$R$
be the
![]() $(\varepsilon,d)$
-reduced graph for some
$(\varepsilon,d)$
-reduced graph for some
![]() $(\varepsilon,d)$
-regular partition
$(\varepsilon,d)$
-regular partition
![]() $V_0,\dots,V_t$
of
$V_0,\dots,V_t$
of
![]() $G$
. Then
$G$
. Then
![]() $R$
contains a matching
$R$
contains a matching
![]() $M$
of size
$M$
of size
![]() $(\alpha +2d)t$
.
$(\alpha +2d)t$
.
For completeness, we give the proof in Appendix A. It follows that we can cover the vertices of
![]() $R$
with cherries
$R$
with cherries
![]() $K_{1,2}$
and matching edges
$K_{1,2}$
and matching edges
![]() $K_{1,1}$
, such that there are not too many cherries.Footnote
2
Before we can apply Lemma 4.2 to each cherry and Lemma 4.3 to each matching edge, some preliminary steps are needed. We remove some vertices from each cherry to make it unbalanced and ensure that both edges are super-regular. Then we cover all vertices that are not contained in any of the cherries or edges by finding a collection of triangles
$K_{1,1}$
, such that there are not too many cherries.Footnote
2
Before we can apply Lemma 4.2 to each cherry and Lemma 4.3 to each matching edge, some preliminary steps are needed. We remove some vertices from each cherry to make it unbalanced and ensure that both edges are super-regular. Then we cover all vertices that are not contained in any of the cherries or edges by finding a collection of triangles
![]() $\mathcal{T}_1$
. We construct another collection of triangles
$\mathcal{T}_1$
. We construct another collection of triangles
![]() $\mathcal{T}_2$
to ensure that in each cherry the relations between the three sets are as required by Lemma 4.2. For constructing
$\mathcal{T}_2$
to ensure that in each cherry the relations between the three sets are as required by Lemma 4.2. For constructing
![]() $\mathcal{T}_1$
and
$\mathcal{T}_1$
and
![]() $\mathcal{T}_2$
, we will mainly rely on the minimum degree condition of
$\mathcal{T}_2$
, we will mainly rely on the minimum degree condition of
![]() $G$
and the fact that in the probability
$G$
and the fact that in the probability
![]() $p \ge C/n$
, the constant
$p \ge C/n$
, the constant
![]() $C$
can be chosen large enough so that a.a.s. the following holds: each linear-sized set contains a random edge and for any not too small part of a regular pair and a linear-sized set there is a triangle containing an edge form the pair and the third vertex from the set. Finally, we can use Lemma 4.2 and Lemma 4.3 to cover the remaining vertices with a collection of triangles
$C$
can be chosen large enough so that a.a.s. the following holds: each linear-sized set contains a random edge and for any not too small part of a regular pair and a linear-sized set there is a triangle containing an edge form the pair and the third vertex from the set. Finally, we can use Lemma 4.2 and Lemma 4.3 to cover the remaining vertices with a collection of triangles
![]() $\mathcal{T}_3$
. Together
$\mathcal{T}_3$
. Together
![]() $\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3$
gives a triangle factor in
$\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3$
gives a triangle factor in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
We mention already now that when
![]() $\alpha$
is sufficiently smaller than
$\alpha$
is sufficiently smaller than
![]() $1/3$
and the condition on the minimum degree of
$1/3$
and the condition on the minimum degree of
![]() $G$
reads as
$G$
reads as
![]() $\delta (G) \ge (\alpha -\gamma )n$
, many of the steps outlined above are not necessary. In this case indeed we do not have to cover all graph with triangles and we only want to find
$\delta (G) \ge (\alpha -\gamma )n$
, many of the steps outlined above are not necessary. In this case indeed we do not have to cover all graph with triangles and we only want to find
![]() $\alpha n$
pairwise vertex-disjoint triangles in
$\alpha n$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
. We will see that an application of Lemmas 4.2 and 4.3 to the cherries and the matching edges found at the beginning (after having made them super-regular and suitable for Lemma 4.2) is already enough to find these
$G \cup G(n,p)$
. We will see that an application of Lemmas 4.2 and 4.3 to the cherries and the matching edges found at the beginning (after having made them super-regular and suitable for Lemma 4.2) is already enough to find these
![]() $\alpha n$
triangles.
$\alpha n$
triangles.
4.3 Sublinear case
Assume
![]() $G$
is an
$G$
is an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta (G) \ge m$
and let
$\delta (G) \ge m$
and let
![]() $p\ge C \log n/n$
. We want to show that a.a.s. there exist
$p\ge C \log n/n$
. We want to show that a.a.s. there exist
![]() $m$
pairwise vertex-disjoint triangles in
$m$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
. Any vertex of large degree in
$G \cup G(n,p)$
. Any vertex of large degree in
![]() $G$
can easily be covered by a triangle later, so we assume an upper bound on the maximum degree
$G$
can easily be covered by a triangle later, so we assume an upper bound on the maximum degree
![]() $\Delta (G)$
of the graph
$\Delta (G)$
of the graph
![]() $G$
. With this condition, we split the proof in three ranges for the value of
$G$
. With this condition, we split the proof in three ranges for the value of
![]() $m$
:
$m$
:
![]() $1 \le m \le (\log n)^3$
,
$1 \le m \le (\log n)^3$
,
![]() $(\log n)^3 \le m \le \sqrt{n}$
, and
$(\log n)^3 \le m \le \sqrt{n}$
, and
![]() $\sqrt{n} \le m \le n/256$
. If
$\sqrt{n} \le m \le n/256$
. If
![]() $1 \le m \le (\log n)^3$
a.a.s.
$1 \le m \le (\log n)^3$
a.a.s.
![]() $m$
pairwise vertex-disjoint triangles already exist in
$m$
pairwise vertex-disjoint triangles already exist in
![]() $G(n,p)$
. If
$G(n,p)$
. If
![]() $(\log n)^3 \le m \le \sqrt{n}$
we will find many large enough vertex-disjoint stars in
$(\log n)^3 \le m \le \sqrt{n}$
we will find many large enough vertex-disjoint stars in
![]() $G$
(see Lemma 7.3) and a.a.s. at least
$G$
(see Lemma 7.3) and a.a.s. at least
![]() $m$
of them will be completed to triangles using edges of
$m$
of them will be completed to triangles using edges of
![]() $G(n,p)$
(see Proposition 7.1). However if
$G(n,p)$
(see Proposition 7.1). However if
![]() $m \gt \sqrt{n}$
we cannot hope to find
$m \gt \sqrt{n}$
we cannot hope to find
![]() $m$
large enough vertex-disjoint stars and instead we will apply a greedy strategy using that a.a.s. every vertex has an edge in its neighbourhood (see Proposition 7.2).
$m$
large enough vertex-disjoint stars and instead we will apply a greedy strategy using that a.a.s. every vertex has an edge in its neighbourhood (see Proposition 7.2).
5. Proof of the extremal theorem
Proof of Theorem 2.3.Let
![]() $0 \lt \alpha _0 \le 1/3$
and choose
$0 \lt \alpha _0 \le 1/3$
and choose
![]() $d=1/2$
. Let
$d=1/2$
. Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $C_{4.1}\gt 0$
be given by Lemma 4.1 on input
$C_{4.1}\gt 0$
be given by Lemma 4.1 on input
![]() $d$
. We can assume
$d$
. We can assume
![]() $\varepsilon \lt 1/5$
and then choose
$\varepsilon \lt 1/5$
and then choose
![]() $0\lt \beta \lt \alpha _0\, \varepsilon/36$
and
$0\lt \beta \lt \alpha _0\, \varepsilon/36$
and
![]() $0\lt \gamma \lt \beta/11$
. With
$0\lt \gamma \lt \beta/11$
. With
![]() $C_{2.4}$
given by Theorem 2.4, let
$C_{2.4}$
given by Theorem 2.4, let
![]() $C \ge 2 C_{2.4} + 1 + 2 C_{4.1}/\alpha _0$
. Finally, let
$C \ge 2 C_{2.4} + 1 + 2 C_{4.1}/\alpha _0$
. Finally, let
![]() $\alpha _0 \le \alpha \le 1/3$
.
$\alpha _0 \le \alpha \le 1/3$
.
Given
![]() $n$
, let
$n$
, let
![]() $p\ge C \log n/n$
. With our choice of
$p\ge C \log n/n$
. With our choice of
![]() $C$
, we can reveal
$C$
, we can reveal
![]() $G(n,p)$
in three rounds
$G(n,p)$
in three rounds
![]() $G_1 \sim G(n,2 C_{2.4} \log n/n)$
,
$G_1 \sim G(n,2 C_{2.4} \log n/n)$
,
![]() $G_2 \sim G(n,\log n/n)$
, and
$G_2 \sim G(n,\log n/n)$
, and
![]() $G_3 \sim G(n,\tfrac{2 C_{4.1}}{\alpha _0} \log n/n)$
. We will only know later in which subset we will use
$G_3 \sim G(n,\tfrac{2 C_{4.1}}{\alpha _0} \log n/n)$
. We will only know later in which subset we will use
![]() $G_1$
and
$G_1$
and
![]() $G_3$
, but we have that a.a.s. there is an edge of
$G_3$
, but we have that a.a.s. there is an edge of
![]() $G_2$
between any two not necessarily disjoint sets of size
$G_2$
between any two not necessarily disjoint sets of size
![]() $\beta n$
. Indeed, fixed two such sets, the probability that there is no edge of
$\beta n$
. Indeed, fixed two such sets, the probability that there is no edge of
![]() $G_2$
is at most
$G_2$
is at most
![]() $(1-\log n/n)^{(\beta n)^2} \le \exp (-\beta ^2 n \log n)$
, and we conclude by an union bound over the at most
$(1-\log n/n)^{(\beta n)^2} \le \exp (-\beta ^2 n \log n)$
, and we conclude by an union bound over the at most
![]() $2^{2n}$
choices for the two sets. Now let
$2^{2n}$
choices for the two sets. Now let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta (G) \ge \left ( \alpha -\gamma \right ) n$
that is
$\delta (G) \ge \left ( \alpha -\gamma \right ) n$
that is
![]() $(\alpha,\beta )$
-stable and define
$(\alpha,\beta )$
-stable and define
![]() $m_0= \max \{ n/3 -\delta (G), n/3-\lfloor \alpha n \rfloor \}$
. Our goal is to a.a.s. find pairwise vertex-disjoint triangles in
$m_0= \max \{ n/3 -\delta (G), n/3-\lfloor \alpha n \rfloor \}$
. Our goal is to a.a.s. find pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
such that at most
$G \cup G(n,p)$
such that at most
![]() $3 m_0$
vertices are left uncovered.
$3 m_0$
vertices are left uncovered.
To aid with calculations we let
![]() $\kappa = n/3 - \lceil \alpha n \rceil$
and observe that
$\kappa = n/3 - \lceil \alpha n \rceil$
and observe that
![]() $\kappa \in \{ 0,-1/3,-2/3 \}$
if
$\kappa \in \{ 0,-1/3,-2/3 \}$
if
![]() $\alpha =1/3$
and that
$\alpha =1/3$
and that
![]() $\kappa \gt 0$
if
$\kappa \gt 0$
if
![]() $\alpha \lt 1/3$
and
$\alpha \lt 1/3$
and
![]() $n$
large enough. Also note that
$n$
large enough. Also note that
![]() $m_0-\kappa$
is an integer and that
$m_0-\kappa$
is an integer and that
![]() $3 \kappa = \lfloor (1-\alpha ) n \rfloor - 2 \lceil \alpha n \rceil$
. With this we set
$3 \kappa = \lfloor (1-\alpha ) n \rfloor - 2 \lceil \alpha n \rceil$
. With this we set
![]() $w = \max \{ 3 \kappa, 0\}$
. As
$w = \max \{ 3 \kappa, 0\}$
. As
![]() $G$
is
$G$
is
![]() $(\alpha, \beta )$
-stable we get a partition of
$(\alpha, \beta )$
-stable we get a partition of
![]() $V(G)$
into sets
$V(G)$
into sets
![]() $A$
and
$A$
and
![]() $B$
satisfying the conditions of Definition 2.1.
$B$
satisfying the conditions of Definition 2.1.
Claim 5.1.
There a.a.s. are a collection of triangles
![]() $\mathcal{T}_1$
in
$\mathcal{T}_1$
in
![]() $G \cup G_1 \cup G_2$
with
$G \cup G_1 \cup G_2$
with
![]() $|\mathcal{T}_1| \le \beta n$
and a set
$|\mathcal{T}_1| \le \beta n$
and a set
![]() $W \subseteq V(G) \setminus V(\mathcal{T}_1)$
with
$W \subseteq V(G) \setminus V(\mathcal{T}_1)$
with
![]() $|W| \le 3 m_0 - w$
such that the following holds. For
$|W| \le 3 m_0 - w$
such that the following holds. For
![]() $A_1=A \setminus (V(\mathcal{T}_1) \cup W)$
and
$A_1=A \setminus (V(\mathcal{T}_1) \cup W)$
and
![]() $B_1=B \setminus (V(\mathcal{T}_1) \cup W)$
, we have that
$B_1=B \setminus (V(\mathcal{T}_1) \cup W)$
, we have that
![]() $|A_1| \le \lceil \alpha n \rceil$
,
$|A_1| \le \lceil \alpha n \rceil$
,
![]() $|B_1|=2|A_1|+w$
, the minimum degree between
$|B_1|=2|A_1|+w$
, the minimum degree between
![]() $A_1$
and
$A_1$
and
![]() $B_1$
is at least
$B_1$
is at least
![]() $\alpha n/5$
, all but at most
$\alpha n/5$
, all but at most
![]() $\beta n$
vertices of
$\beta n$
vertices of
![]() $A_1$
have degree at least
$A_1$
have degree at least
![]() $|B_1| - \beta n$
into
$|B_1| - \beta n$
into
![]() $B_1$
, and all but at most
$B_1$
, and all but at most
![]() $\beta n$
vertices of
$\beta n$
vertices of
![]() $B_1$
have degree at least
$B_1$
have degree at least
![]() $|A_1| - \beta n$
into
$|A_1| - \beta n$
into
![]() $A_1$
.
$A_1$
.
The sets
![]() $A_1$
and
$A_1$
and
![]() $B_1$
partition
$B_1$
partition
![]() $V(G) \setminus (V(\mathcal{T}_1) \cup W)$
and, after proving Claim 5.1, we will cover all but
$V(G) \setminus (V(\mathcal{T}_1) \cup W)$
and, after proving Claim 5.1, we will cover all but
![]() $w$
vertices from
$w$
vertices from
![]() $A_1 \cup B_1$
with additional triangles. Hence, if we manage to find these triangles, we have covered all but
$A_1 \cup B_1$
with additional triangles. Hence, if we manage to find these triangles, we have covered all but
![]() $|W|+w \le 3 m_0$
vertices, as desired. We remark for later that
$|W|+w \le 3 m_0$
vertices, as desired. We remark for later that
![]() $|W| \le 3m_0-w \le 4 \gamma n$
.
$|W| \le 3m_0-w \le 4 \gamma n$
.
Proof of Claim 5.1.We have either
![]() $|B| \gt \lfloor (1-\alpha ) n \rfloor$
or
$|B| \gt \lfloor (1-\alpha ) n \rfloor$
or
![]() $|A| \ge \lceil \alpha n \rceil$
. First suppose that we are in the first case, where
$|A| \ge \lceil \alpha n \rceil$
. First suppose that we are in the first case, where
![]() $|B|=\lfloor (1-\alpha )n \rfloor +m$
for some
$|B|=\lfloor (1-\alpha )n \rfloor +m$
for some
![]() $1 \le m \le \beta n$
(and
$1 \le m \le \beta n$
(and
![]() $|A|=\lceil \alpha n \rceil - m$
), and note that
$|A|=\lceil \alpha n \rceil - m$
), and note that
If
![]() $1 \le m \le m_0 - \kappa$
, then
$1 \le m \le m_0 - \kappa$
, then
![]() $0 \lt 3m \le 3 m_0 - 3 \kappa$
and we let
$0 \lt 3m \le 3 m_0 - 3 \kappa$
and we let
![]() $W$
be any set with
$W$
be any set with
![]() $\min \{3m,3m+3 \kappa \} \le 3m_0-w$
vertices from
$\min \{3m,3m+3 \kappa \} \le 3m_0-w$
vertices from
![]() $B$
. Then with the choice of
$B$
. Then with the choice of
![]() $\mathcal{T}_1=\emptyset$
, we have that the sets
$\mathcal{T}_1=\emptyset$
, we have that the sets
![]() $A_1=A$
and
$A_1=A$
and
![]() $B_1=B \setminus W$
partition
$B_1=B \setminus W$
partition
![]() $V(G) \setminus W$
, and
$V(G) \setminus W$
, and
![]() $|A_1|=\lceil \alpha n \rceil -m$
and
$|A_1|=\lceil \alpha n \rceil -m$
and
![]() $|B_1|=|B|-\min \{ 3m,3m+3 \kappa \}=2|A_1|+ w$
.
$|B_1|=|B|-\min \{ 3m,3m+3 \kappa \}=2|A_1|+ w$
.
If on the other hand,
![]() $m_0 \lt m + \kappa$
, then
$m_0 \lt m + \kappa$
, then
and we observe that
![]() $m-m_0+\kappa$
is an integer. Moreover,
$m-m_0+\kappa$
is an integer. Moreover,
![]() $m-m_0+\kappa \le m \le |B|/256$
, where we use
$m-m_0+\kappa \le m \le |B|/256$
, where we use
![]() $m_0-\kappa \ge 0$
,
$m_0-\kappa \ge 0$
,
![]() $m \le \beta n \le \alpha _0 \varepsilon n/36 \le n/(3 \cdot 5 \cdot 36)$
and
$m \le \beta n \le \alpha _0 \varepsilon n/36 \le n/(3 \cdot 5 \cdot 36)$
and
![]() $|B| = \lfloor (1-\alpha )n \rfloor + m \ge n/2 +m$
. Thus, by Theorem 2.4 and as
$|B| = \lfloor (1-\alpha )n \rfloor + m \ge n/2 +m$
. Thus, by Theorem 2.4 and as
![]() $2 C_{2.4} \log n/n \ge C_{2.4} \log |B|/ |B|$
, we a.a.s. find
$2 C_{2.4} \log n/n \ge C_{2.4} \log |B|/ |B|$
, we a.a.s. find
![]() $m-m_0+\kappa$
pairwise vertex-disjoint triangles in
$m-m_0+\kappa$
pairwise vertex-disjoint triangles in
![]() $(G \cup G_1)[B]$
. Denote by
$(G \cup G_1)[B]$
. Denote by
![]() $\mathcal{T}_1$
the collection of these
$\mathcal{T}_1$
the collection of these
![]() $m-m_0+\kappa$
triangles. Let
$m-m_0+\kappa$
triangles. Let
![]() $W$
be any set of
$W$
be any set of
![]() $3m_0-w$
vertices from
$3m_0-w$
vertices from
![]() $B$
not covered by any triangle in
$B$
not covered by any triangle in
![]() $\mathcal{T}_1$
. Then the sets
$\mathcal{T}_1$
. Then the sets
![]() $A_1=A$
and
$A_1=A$
and
![]() $B_1=B \setminus (V(\mathcal{T}_1) \cup W)$
partition
$B_1=B \setminus (V(\mathcal{T}_1) \cup W)$
partition
![]() $V(G) \setminus (V(\mathcal{T}_1) \cup W)$
, and we have
$V(G) \setminus (V(\mathcal{T}_1) \cup W)$
, and we have
![]() $|A_1|=\lceil \alpha n \rceil -m$
and
$|A_1|=\lceil \alpha n \rceil -m$
and
It remains to consider the second case, where
![]() $|A|= \lceil \alpha n \rceil +m$
for some
$|A|= \lceil \alpha n \rceil +m$
for some
![]() $0 \le m \le \beta n$
. First, we greedily pick
$0 \le m \le \beta n$
. First, we greedily pick
![]() $m$
pairwise vertex-disjoint triangles in
$m$
pairwise vertex-disjoint triangles in
![]() $G \cup G_2$
each with two vertices in
$G \cup G_2$
each with two vertices in
![]() $A$
and one vertex in
$A$
and one vertex in
![]() $B$
. Indeed during the process, there is always a vertex
$B$
. Indeed during the process, there is always a vertex
![]() $v$
in
$v$
in
![]() $B$
, not yet contained in a triangle, with at least
$B$
, not yet contained in a triangle, with at least
![]() $\deg (v,A)-2m \ge (\alpha/4-2\beta )n \ge \beta n$
uncovered neighbours in
$\deg (v,A)-2m \ge (\alpha/4-2\beta )n \ge \beta n$
uncovered neighbours in
![]() $A$
in the graph
$A$
in the graph
![]() $G$
. By the property assumed in
$G$
. By the property assumed in
![]() $G_2$
, we can then find an edge within these neighbours of
$G_2$
, we can then find an edge within these neighbours of
![]() $v$
to get a triangle. Denote by
$v$
to get a triangle. Denote by
![]() $\mathcal{T}_1$
the collection of these
$\mathcal{T}_1$
the collection of these
![]() $m$
triangles.
$m$
triangles.
If
![]() $\kappa \ge 0$
, then, with the choice of
$\kappa \ge 0$
, then, with the choice of
![]() $W=\emptyset$
, we have that
$W=\emptyset$
, we have that
![]() $A_1=A \setminus V(\mathcal{T}_1)$
and
$A_1=A \setminus V(\mathcal{T}_1)$
and
![]() $B_1=B \setminus V(\mathcal{T}_1)$
partition
$B_1=B \setminus V(\mathcal{T}_1)$
partition
![]() $V(G) \setminus V(\mathcal{T}_1)$
and
$V(G) \setminus V(\mathcal{T}_1)$
and
If
![]() $\kappa \lt 0$
, we additionally pick a set
$\kappa \lt 0$
, we additionally pick a set
![]() $W$
of vertices not covered by triangles from
$W$
of vertices not covered by triangles from
![]() $\mathcal{T}_1$
, such that
$\mathcal{T}_1$
, such that
![]() $|W|=1$
,
$|W|=1$
,
![]() $|W \cap A|=1$
,
$|W \cap A|=1$
,
![]() $|W \cap B|=0$
if
$|W \cap B|=0$
if
![]() $\kappa =-2/3$
, and
$\kappa =-2/3$
, and
![]() $|W|=2$
,
$|W|=2$
,
![]() $|W \cap A|=|W\cap B|=1$
if
$|W \cap A|=|W\cap B|=1$
if
![]() $\kappa =-1/3$
. Then, the sets
$\kappa =-1/3$
. Then, the sets
![]() $A_1=A \setminus (V(\mathcal{T}_1) \cup W)$
and
$A_1=A \setminus (V(\mathcal{T}_1) \cup W)$
and
![]() $B_1=B \setminus (V(\mathcal{T}_1) \cup W)$
partition
$B_1=B \setminus (V(\mathcal{T}_1) \cup W)$
partition
![]() $V(G) \setminus (V(\mathcal{T}_1) \cup W)$
, and
$V(G) \setminus (V(\mathcal{T}_1) \cup W)$
, and
![]() $|B_1|=2|A_1|+w$
. Indeed, if
$|B_1|=2|A_1|+w$
. Indeed, if
![]() $\kappa =-2/3$
, we have
$\kappa =-2/3$
, we have
![]() $|A_1|=|A|-2|\mathcal{T}_1|-1=\lceil \alpha n\rceil - m-1$
and
$|A_1|=|A|-2|\mathcal{T}_1|-1=\lceil \alpha n\rceil - m-1$
and
and if
![]() $\kappa =-1/3$
we have
$\kappa =-1/3$
we have
![]() $|A_1|=|A|-2|\mathcal{T}_1|-1=\lceil \alpha n\rceil - m-1$
and
$|A_1|=|A|-2|\mathcal{T}_1|-1=\lceil \alpha n\rceil - m-1$
and
Observe, that in both the first and the second case
![]() $|B_1|=2|A_1|+w$
and
$|B_1|=2|A_1|+w$
and
![]() $|W| \le 3m_0-w$
. Moreover, as we remove at most
$|W| \le 3m_0-w$
. Moreover, as we remove at most
![]() $3m_0-w \le 4 \gamma n \le \alpha n/20$
vertices from each
$3m_0-w \le 4 \gamma n \le \alpha n/20$
vertices from each
![]() $A$
and
$A$
and
![]() $B$
, the minimum degree between
$B$
, the minimum degree between
![]() $A_1$
and
$A_1$
and
![]() $B_1$
is at least
$B_1$
is at least
![]() $\alpha n/4 - \alpha n/20 = \alpha n/5$
. The other conditions on the degrees between
$\alpha n/4 - \alpha n/20 = \alpha n/5$
. The other conditions on the degrees between
![]() $A_1$
and
$A_1$
and
![]() $B_1$
are clearly satisfied, because for all but at most
$B_1$
are clearly satisfied, because for all but at most
![]() $\beta n$
vertices from each set there are still at most
$\beta n$
vertices from each set there are still at most
![]() $\beta n$
non-neighbours in the other set. The bounds
$\beta n$
non-neighbours in the other set. The bounds
![]() $|\mathcal{T}| \le \beta n$
and
$|\mathcal{T}| \le \beta n$
and
![]() $|A_1| \le \lceil \alpha n \rceil$
also hold in all cases.
$|A_1| \le \lceil \alpha n \rceil$
also hold in all cases.
We want to cover all but
![]() $w$
vertices in
$w$
vertices in
![]() $A_1 \cup B_1$
and we start from those vertices in
$A_1 \cup B_1$
and we start from those vertices in
![]() $A_1$
and
$A_1$
and
![]() $B_1$
that do not have a high degree to the other part. We will always cover them with triangles with one vertex in
$B_1$
that do not have a high degree to the other part. We will always cover them with triangles with one vertex in
![]() $A_1$
and two vertices in
$A_1$
and two vertices in
![]() $B_1$
to ensure that the relation between the number of vertices remaining in
$B_1$
to ensure that the relation between the number of vertices remaining in
![]() $A_1$
and
$A_1$
and
![]() $B_1$
does not change. Let
$B_1$
does not change. Let
and observe that
![]() $|\tilde{A_1}|,|\tilde{B_1}| \le \beta n$
.
$|\tilde{A_1}|,|\tilde{B_1}| \le \beta n$
.
We claim that a.a.s. we can greedily pick pairwise vertex-disjoint triangles in
![]() $(G \cup G_2)[A_1 \cup B_1]$
that cover all vertices of
$(G \cup G_2)[A_1 \cup B_1]$
that cover all vertices of
![]() $\tilde{A_1}$
, with each triangle having one vertex in
$\tilde{A_1}$
, with each triangle having one vertex in
![]() $\tilde{A_1}$
and two vertices in
$\tilde{A_1}$
and two vertices in
![]() $B_1 \setminus \tilde{B_1}$
. Indeed, at each step during the process, an uncovered vertex
$B_1 \setminus \tilde{B_1}$
. Indeed, at each step during the process, an uncovered vertex
![]() $v$
in
$v$
in
![]() $\tilde{A_1}$
has at least
$\tilde{A_1}$
has at least
![]() $\deg (v,B_1)- |\tilde{B_1}| - 2 |\tilde{A_1}| \ge (\alpha/5-3 \beta )n \ge \beta n$
uncovered neighbours in
$\deg (v,B_1)- |\tilde{B_1}| - 2 |\tilde{A_1}| \ge (\alpha/5-3 \beta )n \ge \beta n$
uncovered neighbours in
![]() $B_1 \setminus \tilde{B_1}$
in the graph
$B_1 \setminus \tilde{B_1}$
in the graph
![]() $G$
. We then find an edge of
$G$
. We then find an edge of
![]() $G_2$
within these neighbours of
$G_2$
within these neighbours of
![]() $v$
and build a triangle. Denote by
$v$
and build a triangle. Denote by
![]() $\mathcal{T}_2$
the collection of these triangles and note that
$\mathcal{T}_2$
the collection of these triangles and note that
![]() $|\mathcal{T}_2| \le \beta n$
.
$|\mathcal{T}_2| \le \beta n$
.
Observe that at this point
![]() $2 |\mathcal{T}_2| \le 2\beta n$
vertices of
$2 |\mathcal{T}_2| \le 2\beta n$
vertices of
![]() $B_1 \setminus \tilde{B_1}$
have already been covered. We claim that a.a.s. we can greedly pick pairwise vertex-disjoint triangles in
$B_1 \setminus \tilde{B_1}$
have already been covered. We claim that a.a.s. we can greedly pick pairwise vertex-disjoint triangles in
![]() $(G \cup G_2)[(A_1 \cup B_1) \setminus V(\mathcal{T}_2)]$
that cover all vertices of
$(G \cup G_2)[(A_1 \cup B_1) \setminus V(\mathcal{T}_2)]$
that cover all vertices of
![]() $\tilde{B_1}$
, where each triangle has one vertex in
$\tilde{B_1}$
, where each triangle has one vertex in
![]() $A_1 \setminus \tilde{A_1}$
, one vertex in
$A_1 \setminus \tilde{A_1}$
, one vertex in
![]() $\tilde{B_1}$
, and one vertex in
$\tilde{B_1}$
, and one vertex in
![]() $B_1 \setminus \tilde{B_1}$
. Indeed, at each step during the process, an uncovered vertex
$B_1 \setminus \tilde{B_1}$
. Indeed, at each step during the process, an uncovered vertex
![]() $v$
in
$v$
in
![]() $\tilde{B_1}$
has at least
$\tilde{B_1}$
has at least
![]() $\deg (v,A_1) - |\tilde{A_1}| - |\tilde{B_1}| \ge (\alpha/5-2 \beta )n \ge \beta n$
uncovered neighbours in
$\deg (v,A_1) - |\tilde{A_1}| - |\tilde{B_1}| \ge (\alpha/5-2 \beta )n \ge \beta n$
uncovered neighbours in
![]() $A_1 \setminus \tilde{A_1}$
in the graph
$A_1 \setminus \tilde{A_1}$
in the graph
![]() $G$
and at least
$G$
and at least
uncovered neighbours in
![]() $B_1 \setminus \tilde{B_1}$
in the graph
$B_1 \setminus \tilde{B_1}$
in the graph
![]() $G$
. We then find an edge of
$G$
. We then find an edge of
![]() $G_2$
between these two neighbourhood sets to get a triangle. Denote by
$G_2$
between these two neighbourhood sets to get a triangle. Denote by
![]() $\mathcal{T}_3$
the collection of these triangles and note that
$\mathcal{T}_3$
the collection of these triangles and note that
![]() $|\mathcal{T}_3| \le \beta n$
.
$|\mathcal{T}_3| \le \beta n$
.
The sets
![]() $A_2=A_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
and
$A_2=A_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
and
![]() $B_2=B_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
give a partition of the remaining vertices in
$B_2=B_1 \setminus V(\mathcal{T}_2 \cup \mathcal{T}_3)$
give a partition of the remaining vertices in
![]() $V(G) \setminus (V(\mathcal{T}_1) \cup V(\mathcal{T}_2) \cup V(\mathcal{T}_3) \cup W)$
. We have
$V(G) \setminus (V(\mathcal{T}_1) \cup V(\mathcal{T}_2) \cup V(\mathcal{T}_3) \cup W)$
. We have
and
![]() $|B_2|=2|A_2| + w$
. Moreover, the degree from
$|B_2|=2|A_2| + w$
. Moreover, the degree from
![]() $A_2$
to
$A_2$
to
![]() $B_2$
is at least
$B_2$
is at least
![]() $|B_1|-9 \beta n - 2|\mathcal{T}_2 \cup \mathcal{T}_3| = |B_2| - 9 \beta n$
and the degree from
$|B_1|-9 \beta n - 2|\mathcal{T}_2 \cup \mathcal{T}_3| = |B_2| - 9 \beta n$
and the degree from
![]() $B_2$
to
$B_2$
to
![]() $A_2$
is at least
$A_2$
is at least
![]() $|A_1|- 9 \beta n - |\mathcal{T}_2 \cup \mathcal{T}_3| = |A_2| - 9 \beta n$
. We partition
$|A_1|- 9 \beta n - |\mathcal{T}_2 \cup \mathcal{T}_3| = |A_2| - 9 \beta n$
. We partition
![]() $B_2$
arbitrarily into three subsets
$B_2$
arbitrarily into three subsets
![]() $B'_{\!\!1}$
,
$B'_{\!\!1}$
,
![]() ${B''}_{\!\!\!2}$
, and
${B''}_{\!\!\!2}$
, and
![]() $W'$
of size
$W'$
of size
![]() $|B'_{\!\!1}|=|{B''}_{\!\!\!2}|=|A_2|$
and
$|B'_{\!\!1}|=|{B''}_{\!\!\!2}|=|A_2|$
and
![]() $|W'|=|B_2|-2|A_2|=w$
. Then the degree from
$|W'|=|B_2|-2|A_2|=w$
. Then the degree from
![]() $A_2$
to
$A_2$
to
![]() $B'_{\!\!1}$
and the degree from
$B'_{\!\!1}$
and the degree from
![]() $A_2$
to
$A_2$
to
![]() ${B''}_{\!\!\!2}$
are at least
${B''}_{\!\!\!2}$
are at least
![]() $|B'_{\!\!1}| - 9 \beta n$
.
$|B'_{\!\!1}| - 9 \beta n$
.
We claim that the pair
![]() $(A_2,B'_{\!\!1})$
is
$(A_2,B'_{\!\!1})$
is
![]() $(\varepsilon,1/2)$
-super-regular, with
$(\varepsilon,1/2)$
-super-regular, with
![]() $\varepsilon$
being chosen as stated at the beginning of the proof. Indeed for all
$\varepsilon$
being chosen as stated at the beginning of the proof. Indeed for all
![]() $X \subseteq A_2$
and
$X \subseteq A_2$
and
![]() $Y \subseteq B'_{\!\!1}$
with
$Y \subseteq B'_{\!\!1}$
with
![]() $|X| \ge \varepsilon |A_2|$
and
$|X| \ge \varepsilon |A_2|$
and
![]() $|Y| \ge \varepsilon |B'_{\!\!1}|$
, we have
$|Y| \ge \varepsilon |B'_{\!\!1}|$
, we have
and
![]() $\deg (a,B'_{\!\!1}) \ge |B'_{\!\!1}| - 9 \beta n \ge |B'_{\!\!1}|/2$
for all
$\deg (a,B'_{\!\!1}) \ge |B'_{\!\!1}| - 9 \beta n \ge |B'_{\!\!1}|/2$
for all
![]() $a \in A_2$
, and
$a \in A_2$
, and
![]() $\deg (b,A_2) \ge |A_2| - 9 \beta n \ge |A_2|/2$
for all
$\deg (b,A_2) \ge |A_2| - 9 \beta n \ge |A_2|/2$
for all
![]() $b \in B'_{\!\!1}$
, where for all inequalities we use
$b \in B'_{\!\!1}$
, where for all inequalities we use
![]() $\beta \le \alpha/36$
. For the same reason, the pair
$\beta \le \alpha/36$
. For the same reason, the pair
![]() $(A_2,{B''}_{\!\!\!2})$
is
$(A_2,{B''}_{\!\!\!2})$
is
![]() $(\varepsilon,1/2)$
-super-regular as well.
$(\varepsilon,1/2)$
-super-regular as well.
Now, as
![]() $\tfrac{2C_{4.1}}{\alpha _0} \log n/n \ge C_{4.1} \log |A_2|/|A_2|$
, we can apply Lemma 4.1 to
$\tfrac{2C_{4.1}}{\alpha _0} \log n/n \ge C_{4.1} \log |A_2|/|A_2|$
, we can apply Lemma 4.1 to
![]() $A_2$
,
$A_2$
,
![]() $B'_{\!\!1}$
and
$B'_{\!\!1}$
and
![]() ${B''}_{\!\!\!2}$
, with
${B''}_{\!\!\!2}$
, with
![]() $d=1/2$
and
$d=1/2$
and
![]() $\varepsilon$
, and a.a.s. get a triangle factor
$\varepsilon$
, and a.a.s. get a triangle factor
![]() $\mathcal{T}_4$
in
$\mathcal{T}_4$
in
![]() $(G \cup G_3) [V']$
, where
$(G \cup G_3) [V']$
, where
![]() $V'=V(G) \setminus (V(\mathcal{T}_1) \cup V(\mathcal{T}_2) \cup V(\mathcal{T}_3) \cup W \cup W')$
. Then
$V'=V(G) \setminus (V(\mathcal{T}_1) \cup V(\mathcal{T}_2) \cup V(\mathcal{T}_3) \cup W \cup W')$
. Then
![]() $\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3 \cup \mathcal{T}_4$
contains at least
$\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3 \cup \mathcal{T}_4$
contains at least
pairwise vertex-disjoint triangles covering
![]() $V(G) \setminus (W \cup W')$
.
$V(G) \setminus (W \cup W')$
.
We point out that under certain conditions our proof of Theorem 2.3 gives more triangles. When
![]() $\alpha \lt 1/3$
and
$\alpha \lt 1/3$
and
![]() $|A| \ge \alpha n$
, as
$|A| \ge \alpha n$
, as
![]() $|W| \le 3m_0-w$
, we get
$|W| \le 3m_0-w$
, we get
![]() $\lceil \alpha n \rceil$
pairwise vertex-disjoint triangles in
$\lceil \alpha n \rceil$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
, even when
$G \cup G(n,p)$
, even when
![]() $\delta (G) \lt \alpha n$
. Similarly, when
$\delta (G) \lt \alpha n$
. Similarly, when
![]() $\alpha = 1/3$
and
$\alpha = 1/3$
and
![]() $|A| \ge n/3$
, as
$|A| \ge n/3$
, as
![]() $|W| \le 2$
, we get
$|W| \le 2$
, we get
![]() $\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles in
$\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
, even when
$G \cup G(n,p)$
, even when
![]() $\delta (G) \lt n/3$
. Moreover, for any value of
$\delta (G) \lt n/3$
. Moreover, for any value of
![]() $\alpha$
, when
$\alpha$
, when
![]() $|A|-n/3\gt 0$
is linear in
$|A|-n/3\gt 0$
is linear in
![]() $n$
, we could use Lemma 4.2 instead of Lemma 4.1 to avoid the
$n$
, we could use Lemma 4.2 instead of Lemma 4.1 to avoid the
![]() $\log n$
-factor in the probability.
$\log n$
-factor in the probability.
6. Proof of the stability theorem
Proof of Theorem 2.2.We start by defining necessary constants. Given
![]() $0\lt \beta \lt 1/12$
, let
$0\lt \beta \lt 1/12$
, let
![]() $d\gt 0$
be obtained from Lemma 4.4, and set
$d\gt 0$
be obtained from Lemma 4.4, and set
![]() $\gamma =d/2$
and
$\gamma =d/2$
and
![]() $t_0=11/d$
. Next, we take any
$t_0=11/d$
. Next, we take any
![]() $0\lt \delta ' \lt 160^{-2} d^2$
and use Lemma 4.2 on input
$0\lt \delta ' \lt 160^{-2} d^2$
and use Lemma 4.2 on input
![]() $d/2$
and
$d/2$
and
![]() $\delta '$
to obtain
$\delta '$
to obtain
![]() $\delta _0, \delta, \varepsilon '$
with
$\delta _0, \delta, \varepsilon '$
with
![]() $\delta ' \ge \delta _0\gt \delta \gt \varepsilon '\gt 0$
and
$\delta ' \ge \delta _0\gt \delta \gt \varepsilon '\gt 0$
and
![]() $C_1$
. Additionally, we assume that
$C_1$
. Additionally, we assume that
![]() $C_1$
is large enough and
$C_1$
is large enough and
![]() $\varepsilon '$
is small enough for Lemma 4.3 to hold with input
$\varepsilon '$
is small enough for Lemma 4.3 to hold with input
![]() $d/2$
. Finally, let
$d/2$
. Finally, let
![]() $C_2$
be given by Lemma 3.2 on input
$C_2$
be given by Lemma 3.2 on input
![]() $d/2$
. We let
$d/2$
. We let
![]() $0\lt \varepsilon \le \varepsilon '/2$
. In summary, the dependencies between our constants are as follows:
$0\lt \varepsilon \le \varepsilon '/2$
. In summary, the dependencies between our constants are as follows:
We apply Lemma 3.5 with
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $t_0$
to obtain
$t_0$
to obtain
![]() $T$
. We take
$T$
. We take
![]() $C$
large enough such that, for
$C$
large enough such that, for
![]() $p \ge C/n$
, the random graph
$p \ge C/n$
, the random graph
![]() $G(n,p)$
contains the union
$G(n,p)$
contains the union
![]() $G_1 \cup G_2 \cup G_3$
, where
$G_1 \cup G_2 \cup G_3$
, where
![]() $G_1 \sim G(n,2C_1T/n)$
,
$G_1 \sim G(n,2C_1T/n)$
,
![]() $G_2 \sim G(n,4C_2T/(dn))$
, and
$G_2 \sim G(n,4C_2T/(dn))$
, and
![]() $G_3 \sim G(n,96 T^2/(d^2n))$
.
$G_3 \sim G(n,96 T^2/(d^2n))$
.
Now, for any
![]() $\alpha$
with
$\alpha$
with
![]() $4 \beta \le \alpha \le 1/3$
, let
$4 \beta \le \alpha \le 1/3$
, let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph on the vertex set
$n$
-vertex graph on the vertex set
![]() $V$
with minimum degree
$V$
with minimum degree
![]() $\delta (G) \ge (\alpha -\gamma )n$
that is not
$\delta (G) \ge (\alpha -\gamma )n$
that is not
![]() $(\alpha,\beta )$
-stable. With the regularity lemma (Lemma 3.5) applied to
$(\alpha,\beta )$
-stable. With the regularity lemma (Lemma 3.5) applied to
![]() $G$
, we get
$G$
, we get
![]() $G'$
,
$G'$
,
![]() $t_0 \lt t+1 \le T$
and a partition
$t_0 \lt t+1 \le T$
and a partition
![]() $V_0,\dots,V_t$
of
$V_0,\dots,V_t$
of
![]() $V(G)$
such that (P1)–(P4) hold. Define
$V(G)$
such that (P1)–(P4) hold. Define
![]() $n_0=|V_1|=|V_2|=\dots =|V_t|$
and observe that
$n_0=|V_1|=|V_2|=\dots =|V_t|$
and observe that
![]() $(1-\varepsilon )n/t \le n_0 \le n/t$
. We denote by
$(1-\varepsilon )n/t \le n_0 \le n/t$
. We denote by
![]() $R$
the
$R$
the
![]() $(\varepsilon,d)$
-reduced graph for
$(\varepsilon,d)$
-reduced graph for
![]() $G$
, that is, the graph on the vertex set
$G$
, that is, the graph on the vertex set
![]() $[t]$
with edges
$[t]$
with edges
![]() $ij$
corresponding to
$ij$
corresponding to
![]() $\varepsilon$
-regular pairs
$\varepsilon$
-regular pairs
![]() $(V_i,V_j)$
of density at least
$(V_i,V_j)$
of density at least
![]() $d$
in
$d$
in
![]() $G'$
. We observe that the minimum degree of
$G'$
. We observe that the minimum degree of
![]() $R$
satisfies
$R$
satisfies
![]() $\delta (R) \ge (\alpha -2d) t$
because, otherwise, thre would be vertices with degree at most
$\delta (R) \ge (\alpha -2d) t$
because, otherwise, thre would be vertices with degree at most
![]() $(\alpha -2d)t(n/t)+\varepsilon n \lt (\alpha - \gamma )n - (d+\varepsilon )n$
in
$(\alpha -2d)t(n/t)+\varepsilon n \lt (\alpha - \gamma )n - (d+\varepsilon )n$
in
![]() $G'$
, contradicting (P2).
$G'$
, contradicting (P2).
The purpose of
![]() $G_1$
will become clear later, but we describe some useful properties of
$G_1$
will become clear later, but we describe some useful properties of
![]() $G_2$
and
$G_2$
and
![]() $G_3$
now. Let
$G_3$
now. Let
![]() $U$
and
$U$
and
![]() $W$
be any two clusters that give an edge in
$W$
be any two clusters that give an edge in
![]() $R$
,
$R$
,
![]() $V$
any cluster, and
$V$
any cluster, and
![]() $U' \subseteq U$
,
$U' \subseteq U$
,
![]() $W'\subseteq W$
,
$W'\subseteq W$
,
![]() $V'\subseteq V$
three pairwise disjoint subsets each of size
$V'\subseteq V$
three pairwise disjoint subsets each of size
![]() $dn_0/2$
. Then, with
$dn_0/2$
. Then, with
![]() $G_2$
and as
$G_2$
and as
![]() $4C_2T/(dn) \ge 2C_2/(dn_0)$
, by Lemma 3.2 we have that with probability at least
$4C_2T/(dn) \ge 2C_2/(dn_0)$
, by Lemma 3.2 we have that with probability at least
![]() $1-2^{-4(dn_0/2)/(d/2)}=1-2^{-4n_0}$
$1-2^{-4(dn_0/2)/(d/2)}=1-2^{-4n_0}$
With a union bound over the at most
![]() $t^32^{3n_0}$
choices for
$t^32^{3n_0}$
choices for
![]() $U$
,
$U$
,
![]() $W$
,
$W$
,
![]() $V$
and
$V$
and
![]() $U'$
,
$U'$
,
![]() $W'$
,
$W'$
,
![]() $V'$
, we conclude that a.a.s. (1) holds for all choices as above.
$V'$
, we conclude that a.a.s. (1) holds for all choices as above.
With
![]() $G_3$
we a.a.s. have that
$G_3$
we a.a.s. have that
In fact, given any set
![]() $A$
of size at least
$A$
of size at least
![]() $dn_0/2$
, the expected number of edges of
$dn_0/2$
, the expected number of edges of
![]() $G_3$
in
$G_3$
in
![]() $A$
is
$A$
is
where we used that
![]() $n/n_0 \le t/(1-\varepsilon ) \le 2T$
. Therefore, the probability that the set
$n/n_0 \le t/(1-\varepsilon ) \le 2T$
. Therefore, the probability that the set
![]() $A$
does not contain an edge of
$A$
does not contain an edge of
![]() $G_3$
is at most
$G_3$
is at most
![]() $(1-\frac{96 T^2}{d^2 n})^{\binom{|A|}{2}} \le \exp \left (-\binom{|A|}{2} \cdot \frac{96 T^2}{d^2 n}\right ) \le \exp (-2n)$
and (2) follows from a union bound over the at most
$(1-\frac{96 T^2}{d^2 n})^{\binom{|A|}{2}} \le \exp \left (-\binom{|A|}{2} \cdot \frac{96 T^2}{d^2 n}\right ) \le \exp (-2n)$
and (2) follows from a union bound over the at most
![]() $2^n$
choices for
$2^n$
choices for
![]() $A$
.
$A$
.
Now let
![]() $M_1$
be a largest matching in
$M_1$
be a largest matching in
![]() $R$
. Since
$R$
. Since
![]() $G$
is not
$G$
is not
![]() $(\alpha,\beta )$
-stable, using Lemma 4.4, we conclude that
$(\alpha,\beta )$
-stable, using Lemma 4.4, we conclude that
![]() $|M_1| \ge (\alpha + 2d)t$
. At this point, for the sake of clarity, we split our proof into two cases –
$|M_1| \ge (\alpha + 2d)t$
. At this point, for the sake of clarity, we split our proof into two cases –
![]() $0 \lt \alpha \lt 1/3 - d/3$
and
$0 \lt \alpha \lt 1/3 - d/3$
and
![]() $1/3 - d/3 \le \alpha \le 1/3$
– although some steps will be the same. The first case is indeed much easier, as we do not need to cover all the graph with triangles, while in the second case we are looking for a spanning structure and we want to find
$1/3 - d/3 \le \alpha \le 1/3$
– although some steps will be the same. The first case is indeed much easier, as we do not need to cover all the graph with triangles, while in the second case we are looking for a spanning structure and we want to find
![]() $\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles.
$\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles.
Case
![]() $0 \lt \alpha \lt 1/3 - d/3$
$0 \lt \alpha \lt 1/3 - d/3$
As
![]() $M_1$
is a largest matching in
$M_1$
is a largest matching in
![]() $R$
, the set
$R$
, the set
![]() $V(R) \setminus V(M_1)$
is independent and only one endpoint of each edge of
$V(R) \setminus V(M_1)$
is independent and only one endpoint of each edge of
![]() $M_1$
can be adjacent to more than one vertex from
$M_1$
can be adjacent to more than one vertex from
![]() $V(R) \setminus V(M_1)$
. Therefore, we can greedily pick a second matching
$V(R) \setminus V(M_1)$
. Therefore, we can greedily pick a second matching
![]() $M_2$
such that each edge of
$M_2$
such that each edge of
![]() $M_2$
contains a vertex of
$M_2$
contains a vertex of
![]() $V(R) \setminus V(M_1)$
and a vertex of
$V(R) \setminus V(M_1)$
and a vertex of
![]() $V(M_1)$
, and
$V(M_1)$
, and
![]() $M_2$
covers at least
$M_2$
covers at least
![]() $\min \{|V(R) \setminus V(M_1)|,\delta (R) \}$
vertices of
$\min \{|V(R) \setminus V(M_1)|,\delta (R) \}$
vertices of
![]() $V(R) \setminus V(M_1)$
. The two matchings
$V(R) \setminus V(M_1)$
. The two matchings
![]() $M_1$
and
$M_1$
and
![]() $M_2$
together cover a subset
$M_2$
together cover a subset
![]() $V(M_1 \cup M_2) \subseteq V(R)$
of
$V(M_1 \cup M_2) \subseteq V(R)$
of
vertices, and we can extract a collection of
![]() $|M_2|$
vertex-disjoint cherries and a disjoint matching that cover such vertices. This gives a subgraph
$|M_2|$
vertex-disjoint cherries and a disjoint matching that cover such vertices. This gives a subgraph
![]() $R'\subseteq R$
consisting of cherries and a matching such that for all edges
$R'\subseteq R$
consisting of cherries and a matching such that for all edges
![]() $ij \in E(R')$
the pair
$ij \in E(R')$
the pair
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\varepsilon$
-regular of density at least
$\varepsilon$
-regular of density at least
![]() $d$
in
$d$
in
![]() $G'$
, and therefore in
$G'$
, and therefore in
![]() $G$
as well. We denote by
$G$
as well. We denote by
![]() $\mathcal{J} \subseteq [t]$
the indices of the clusters
$\mathcal{J} \subseteq [t]$
the indices of the clusters
![]() $V_i$
of the cherries and the matching edges in
$V_i$
of the cherries and the matching edges in
![]() $R'$
and we observe from above that
$R'$
and we observe from above that
![]() $|\mathcal{J}| \ge (3 \alpha + d)t$
. We add to
$|\mathcal{J}| \ge (3 \alpha + d)t$
. We add to
![]() $V_0$
all the vertices of
$V_0$
all the vertices of
![]() $G$
that are in the clusters
$G$
that are in the clusters
![]() $V_j$
for
$V_j$
for
![]() $j \notin \mathcal{J}$
.
$j \notin \mathcal{J}$
.
Then we make all pairs associated with the edges of
![]() $R'$
super-regular. Given a pair
$R'$
super-regular. Given a pair
![]() $(A,B)$
, by Lemma 3.3, all but at most
$(A,B)$
, by Lemma 3.3, all but at most
![]() $\varepsilon n_0$
vertices of
$\varepsilon n_0$
vertices of
![]() $A$
(resp.
$A$
(resp.
![]() $B$
) have degree at least
$B$
) have degree at least
![]() $(d-\varepsilon )n_0$
to
$(d-\varepsilon )n_0$
to
![]() $B$
(resp.
$B$
(resp.
![]() $A$
). For every such pair we remove these vertices from
$A$
). For every such pair we remove these vertices from
![]() $A$
and
$A$
and
![]() $B$
, and remove additional vertices to ensure all clusters have the same size. As
$B$
, and remove additional vertices to ensure all clusters have the same size. As
![]() $R'$
only contains vertex-disjoint cherries and a disjoint matching, we can achieve that by removing a total of at most
$R'$
only contains vertex-disjoint cherries and a disjoint matching, we can achieve that by removing a total of at most
![]() $2 \varepsilon n_0$
vertices from each cluster. We add all the removed vertices to
$2 \varepsilon n_0$
vertices from each cluster. We add all the removed vertices to
![]() $V_0$
. Observe that afterwards all the pairs
$V_0$
. Observe that afterwards all the pairs
![]() $(A,B)$
associated with the edges of
$(A,B)$
associated with the edges of
![]() $R'$
are
$R'$
are
![]() $(2\varepsilon,d-3\varepsilon )$
-super-regular, because every vertex
$(2\varepsilon,d-3\varepsilon )$
-super-regular, because every vertex
![]() $a \in A$
has degree at least
$a \in A$
has degree at least
![]() $(d-\varepsilon )n_0 - 2\varepsilon n_0 \ge (d-3\varepsilon )|B|$
into
$(d-\varepsilon )n_0 - 2\varepsilon n_0 \ge (d-3\varepsilon )|B|$
into
![]() $B$
, and every vertex
$B$
, and every vertex
![]() $b \in B$
has degree at least
$b \in B$
has degree at least
![]() $(d-3\varepsilon )|A|$
into
$(d-3\varepsilon )|A|$
into
![]() $A$
.
$A$
.
Recall that for a later application of Lemma 4.2, we need that for each cherry the sizes of the leaf-clusters are smaller than the size of the centre-cluster. Thus, for each cherry
![]() $ijk$
of
$ijk$
of
![]() $R'$
, with
$R'$
, with
![]() $j$
being the centre, we additionally remove
$j$
being the centre, we additionally remove
![]() $\delta |V_j| \le \delta n_0$
vertices from the leaves
$\delta |V_j| \le \delta n_0$
vertices from the leaves
![]() $V_i$
and
$V_i$
and
![]() $V_k$
, and add them to
$V_k$
, and add them to
![]() $V_0$
. We have
$V_0$
. We have
![]() $|V_i|=|V_k|=(1-\delta )|V_j|$
that implies
$|V_i|=|V_k|=(1-\delta )|V_j|$
that implies
![]() $|V_i|=|V_k| \ge (1-\delta _0)|V_j|$
, as
$|V_i|=|V_k| \ge (1-\delta _0)|V_j|$
, as
![]() $\delta _0 \gt \delta$
. We have that all edges of
$\delta _0 \gt \delta$
. We have that all edges of
![]() $R'$
still give
$R'$
still give
![]() $(2\varepsilon,d-3\varepsilon -\delta )$
-super-regular pairs. Moreover,
$(2\varepsilon,d-3\varepsilon -\delta )$
-super-regular pairs. Moreover,
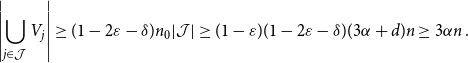 \begin{equation*} \left | \bigcup _{j \in \mathcal {J}} V_j \right | \ge (1-2\varepsilon -\delta ) n_0 |\mathcal {J}| \ge (1-\varepsilon )(1-2\varepsilon -\delta )(3\alpha +d) n \ge 3 \alpha n\, . \end{equation*}
\begin{equation*} \left | \bigcup _{j \in \mathcal {J}} V_j \right | \ge (1-2\varepsilon -\delta ) n_0 |\mathcal {J}| \ge (1-\varepsilon )(1-2\varepsilon -\delta )(3\alpha +d) n \ge 3 \alpha n\, . \end{equation*}
We can assume (by moving only a few additional vertices to
![]() $V_0$
that do not harm the bounds above) that for all cherries and matching edges in
$V_0$
that do not harm the bounds above) that for all cherries and matching edges in
![]() $R'$
the number of vertices in the clusters together is divisible by three.
$R'$
the number of vertices in the clusters together is divisible by three.
For each such super-regular cherry
![]() $ijk$
of
$ijk$
of
![]() $R'$
, after revealing
$R'$
, after revealing
![]() $G_1[V_i \cup V_j \cup V_k]$
we find by Lemma 4.2 a.a.s. a triangle factor covering all the vertices in
$G_1[V_i \cup V_j \cup V_k]$
we find by Lemma 4.2 a.a.s. a triangle factor covering all the vertices in
![]() $V_i \cup V_j \cup V_k$
. Similarly for any matching edge
$V_i \cup V_j \cup V_k$
. Similarly for any matching edge
![]() $ij$
of
$ij$
of
![]() $R'$
, after revealing
$R'$
, after revealing
![]() $G_1[V_i \cup V_j]$
we find by Lemma 4.3 a.a.s. a triangle factor covering all the vertices in
$G_1[V_i \cup V_j]$
we find by Lemma 4.3 a.a.s. a triangle factor covering all the vertices in
![]() $V_i \cup V_j$
. Note that we apply Lemmas 4.2 and 4.3 only constantly many times and thus a.a.s. we get a triangle factor in all such applications. Let
$V_i \cup V_j$
. Note that we apply Lemmas 4.2 and 4.3 only constantly many times and thus a.a.s. we get a triangle factor in all such applications. Let
![]() $\mathcal{T}$
be the union of all such triangle factors. Then
$\mathcal{T}$
be the union of all such triangle factors. Then
![]() $\mathcal{T}$
covers
$\mathcal{T}$
covers
![]() $\left |\bigcup _{j \in \mathcal{J}} V_j \right | \ge 3 \alpha n$
vertices and gives at least
$\left |\bigcup _{j \in \mathcal{J}} V_j \right | \ge 3 \alpha n$
vertices and gives at least
![]() $\alpha n=\min \{\alpha n, \lfloor n/3 \rfloor \}$
pairwise vertex-disjoint triangles in
$\alpha n=\min \{\alpha n, \lfloor n/3 \rfloor \}$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
Case
![]() $1/3 - d/3 \le \alpha \le 1/3$
$1/3 - d/3 \le \alpha \le 1/3$
As discussed in the overview, here we cannot directly apply Lemmas 4.2 and 4.3 as in the case
![]() $0 \lt \alpha \lt 1/3-d/3$
, but we need additional steps. However, even with a lower minimum degree, we will cover all vertices of
$0 \lt \alpha \lt 1/3-d/3$
, but we need additional steps. However, even with a lower minimum degree, we will cover all vertices of
![]() $G$
and find
$G$
and find
![]() $\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles. Recall that
$\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles. Recall that
![]() $M_1$
is a largest matching and that
$M_1$
is a largest matching and that
![]() $|M_1| \ge (\alpha +2d)t$
. Then the set
$|M_1| \ge (\alpha +2d)t$
. Then the set
![]() $V(R) \setminus V(M_1)$
is independent, has size
$V(R) \setminus V(M_1)$
is independent, has size
and only one endpoint of each edge of
![]() $M_1$
can be adjacent to more than one vertex from
$M_1$
can be adjacent to more than one vertex from
![]() $V(R) \setminus V(M_1)$
. Given that
$V(R) \setminus V(M_1)$
. Given that
![]() $\delta (R) \ge (\alpha -2d)t$
, we can greedily pick a second matching
$\delta (R) \ge (\alpha -2d)t$
, we can greedily pick a second matching
![]() $M_2$
such that each edge of
$M_2$
such that each edge of
![]() $M_2$
contains a vertex of
$M_2$
contains a vertex of
![]() $V(R) \setminus V(M_1)$
and a vertex of
$V(R) \setminus V(M_1)$
and a vertex of
![]() $V(M_1)$
, and
$V(M_1)$
, and
![]() $M_2$
covers the remaining vertices
$M_2$
covers the remaining vertices
![]() $V(R) \setminus V(M_1)$
completely. Therefore, the two matchings
$V(R) \setminus V(M_1)$
completely. Therefore, the two matchings
![]() $M_1$
and
$M_1$
and
![]() $M_2$
together cover the vertex set
$M_2$
together cover the vertex set
![]() $V(R)$
and we can extract a collection of
$V(R)$
and we can extract a collection of
![]() $\ell = |M_2| \le (\alpha -3d)t$
vertex-disjoint cherries and a disjoint matching that cover
$\ell = |M_2| \le (\alpha -3d)t$
vertex-disjoint cherries and a disjoint matching that cover
![]() $V(R)$
.
$V(R)$
.
This gives a spanning subgraph
![]() $R'\subseteq R$
on vertex set
$R'\subseteq R$
on vertex set
![]() $[t]$
containing
$[t]$
containing
![]() $\ell \le (\alpha -3d)t$
cherries and a matching of size
$\ell \le (\alpha -3d)t$
cherries and a matching of size
![]() $(t-3\ell )/2 \ge (1-3 \alpha + 9d)t/2 \ge 9dt/2$
such that for all edges
$(t-3\ell )/2 \ge (1-3 \alpha + 9d)t/2 \ge 9dt/2$
such that for all edges
![]() $ij \in E(R')$
the pair
$ij \in E(R')$
the pair
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\varepsilon$
-regular of density at least
$\varepsilon$
-regular of density at least
![]() $d$
in
$d$
in
![]() $G'$
, and therefore in
$G'$
, and therefore in
![]() $G$
as well. We denote by
$G$
as well. We denote by
![]() $\mathcal{I} \subseteq [t]$
the indices of the clusters
$\mathcal{I} \subseteq [t]$
the indices of the clusters
![]() $V_i$
that are not the centre of a cherry in
$V_i$
that are not the centre of a cherry in
![]() $R'$
. As above, with Lemma 3.3, we can make the pairs associated with the edges of
$R'$
. As above, with Lemma 3.3, we can make the pairs associated with the edges of
![]() $R'$
$R'$
![]() $(2\varepsilon,d-3\varepsilon )$
-super-regular, while keeping the clusters all of the same size. For this we have to remove at most
$(2\varepsilon,d-3\varepsilon )$
-super-regular, while keeping the clusters all of the same size. For this we have to remove at most
![]() $t 2 \varepsilon n_0 \le t 2 \varepsilon n/t = 2 \varepsilon n$
vertices, which we add to
$t 2 \varepsilon n_0 \le t 2 \varepsilon n/t = 2 \varepsilon n$
vertices, which we add to
![]() $V_0$
. Next, as for a later application of Lemma 4.2 we need that for each cherry the sizes of the leaf-clusters are smaller than the size of the centre-cluster, we remove for each
$V_0$
. Next, as for a later application of Lemma 4.2 we need that for each cherry the sizes of the leaf-clusters are smaller than the size of the centre-cluster, we remove for each
![]() $i \in \mathcal{I}$
additionally
$i \in \mathcal{I}$
additionally
![]() $\delta |V_i| \le \delta n_0 \le \delta n/t$
vertices from
$\delta |V_i| \le \delta n_0 \le \delta n/t$
vertices from
![]() $V_i$
and add them to
$V_i$
and add them to
![]() $V_0$
. Note that we remove vertices from the clusters of matching edges as well, although this is not necessary. We then get
$V_0$
. Note that we remove vertices from the clusters of matching edges as well, although this is not necessary. We then get
![]() $|V_0| \le \varepsilon n + 2 \varepsilon n + t \delta n/t \le 2 \delta n$
. We can assume (by moving only a few additional vertices to
$|V_0| \le \varepsilon n + 2 \varepsilon n + t \delta n/t \le 2 \delta n$
. We can assume (by moving only a few additional vertices to
![]() $V_0$
that do not harm the bounds above) that for all cherries and matching edges in
$V_0$
that do not harm the bounds above) that for all cherries and matching edges in
![]() $R'$
the number of vertices in the clusters together is divisible by three. By removing
$R'$
the number of vertices in the clusters together is divisible by three. By removing
![]() $n \pmod 3 \in \{0,1,2\}$
vertices from
$n \pmod 3 \in \{0,1,2\}$
vertices from
![]() $V_0$
, we also have
$V_0$
, we also have
![]() $|V_0| \equiv 0 \pmod 3$
; note that this only happens when
$|V_0| \equiv 0 \pmod 3$
; note that this only happens when
![]() $n$
is not divisible by
$n$
is not divisible by
![]() $3$
and we can discard these vertices.
$3$
and we can discard these vertices.
Covering
![]() $V_0$
with triangles. We now want to cover the exceptional vertices in
$V_0$
with triangles. We now want to cover the exceptional vertices in
![]() $V_0$
by triangles. It would be easy to do this greedily by just using (2), but it might happen that afterwards in many of the cherries the number of vertices is not divisible by three or that the centre cluster gets too small. To avoid both these issues, we will cover
$V_0$
by triangles. It would be easy to do this greedily by just using (2), but it might happen that afterwards in many of the cherries the number of vertices is not divisible by three or that the centre cluster gets too small. To avoid both these issues, we will cover
![]() $V_0$
while using the same number of vertices from clusters that are together in a cherry or matching edge. For this we will always cover three vertices at a time and combine (1) with (2) to find additional triangles. Observe that
$V_0$
while using the same number of vertices from clusters that are together in a cherry or matching edge. For this we will always cover three vertices at a time and combine (1) with (2) to find additional triangles. Observe that
![]() $|V_0 \cup \bigcup _{i \not \in \mathcal{I} } V_i| \le 2 \delta n + \ell n/t \le (\alpha -\gamma )n - 2dn$
and, therefore, any
$|V_0 \cup \bigcup _{i \not \in \mathcal{I} } V_i| \le 2 \delta n + \ell n/t \le (\alpha -\gamma )n - 2dn$
and, therefore, any
![]() $v \in V_0$
has at least
$v \in V_0$
has at least
![]() $2 dn$
neighbours in
$2 dn$
neighbours in
![]() $\bigcup _{i \in \mathcal{I}} V_i$
.
$\bigcup _{i \in \mathcal{I}} V_i$
.
Assume we have already covered
![]() $V' \subseteq V_0$
vertices of
$V' \subseteq V_0$
vertices of
![]() $V_0$
using at most
$V_0$
using at most
![]() $5|V'|$
triangles in total. Let
$5|V'|$
triangles in total. Let
![]() $W'$
be the set of vertices from
$W'$
be the set of vertices from
![]() $\bigcup _{i \in \mathcal{I}} V_i$
used for the triangles covering
$\bigcup _{i \in \mathcal{I}} V_i$
used for the triangles covering
![]() $V'$
and note that
$V'$
and note that
![]() $|W'| \le 30 \delta n$
. Then let
$|W'| \le 30 \delta n$
. Then let
![]() $\mathcal{I}' \subseteq \mathcal{I}$
be the set of indices of clusters
$\mathcal{I}' \subseteq \mathcal{I}$
be the set of indices of clusters
![]() $V_i$
with
$V_i$
with
![]() $i \in \mathcal{I}$
which intersect
$i \in \mathcal{I}$
which intersect
![]() $W'$
in at least
$W'$
in at least
![]() $\sqrt{\delta }n_0$
vertices and note that
$\sqrt{\delta }n_0$
vertices and note that
![]() $|\mathcal{I}'| \le |W'|/(\sqrt{\delta }n_0) \le 30 \sqrt{\delta } t/ (1-\varepsilon ) \le 40 \sqrt{\delta } t \le dt/4$
. Moreover, notice that as for each
$|\mathcal{I}'| \le |W'|/(\sqrt{\delta }n_0) \le 30 \sqrt{\delta } t/ (1-\varepsilon ) \le 40 \sqrt{\delta } t \le dt/4$
. Moreover, notice that as for each
![]() $v \in V_0$
we have
$v \in V_0$
we have
![]() $\deg _G(v,\bigcup _{i \in \mathcal{I}} V_i) \ge 2dn$
, there are at least
$\deg _G(v,\bigcup _{i \in \mathcal{I}} V_i) \ge 2dn$
, there are at least
![]() $dt$
indices
$dt$
indices
![]() $i \in \mathcal{I}$
such that
$i \in \mathcal{I}$
such that
![]() $v$
has at least
$v$
has at least
![]() $dn_0$
neighbours in
$dn_0$
neighbours in
![]() $V_i$
. In particular, as
$V_i$
. In particular, as
![]() $|\mathcal{I}'| \le dt/4$
and
$|\mathcal{I}'| \le dt/4$
and
![]() $t \ge 10/d$
, there are at least
$t \ge 10/d$
, there are at least
![]() $dt-|\mathcal{I}'| \ge 3dt/4 \ge 7$
indices
$dt-|\mathcal{I}'| \ge 3dt/4 \ge 7$
indices
![]() $i \in \mathcal{I} \setminus \mathcal{I}'$
such that
$i \in \mathcal{I} \setminus \mathcal{I}'$
such that
![]() $v$
has at least
$v$
has at least
![]() $dn_0$
neighbours in
$dn_0$
neighbours in
![]() $V_i$
. Therefore, we can pick three vertices
$V_i$
. Therefore, we can pick three vertices
![]() $v_1,v_2,v_3 \in V_0 \setminus V'$
and three indices
$v_1,v_2,v_3 \in V_0 \setminus V'$
and three indices
![]() $i_1,i_2,i_3$
in
$i_1,i_2,i_3$
in
![]() $\mathcal{I} \setminus \mathcal{I}'$
such that
$\mathcal{I} \setminus \mathcal{I}'$
such that
![]() $v_j$
has
$v_j$
has
![]() $dn_0$
neighbours in
$dn_0$
neighbours in
![]() $V_{i_j}$
for
$V_{i_j}$
for
![]() $j=1,2,3$
and the clusters
$j=1,2,3$
and the clusters
![]() $V_{i_1},V_{i_2},V_{i_3}$
belong to pairwise different cherries or matching edges. For
$V_{i_1},V_{i_2},V_{i_3}$
belong to pairwise different cherries or matching edges. For
![]() $j=1,2,3$
with (2), we find an edge
$j=1,2,3$
with (2), we find an edge
![]() $e_j$
in
$e_j$
in
![]() $G_3[N(v_j,V_{i_j}) \setminus W']$
and we cover the three vertices with triangles. It is easy to show that we can find at most
$G_3[N(v_j,V_{i_j}) \setminus W']$
and we cover the three vertices with triangles. It is easy to show that we can find at most
![]() $10$
additional triangles with the help of (1) and (2), in such a way that, overall, for each cherry and matching edge, we use the same number of vertices from each of their clusters; in particular, the number of vertices used from each cherry and matching edge is divisible by three. The clusters
$10$
additional triangles with the help of (1) and (2), in such a way that, overall, for each cherry and matching edge, we use the same number of vertices from each of their clusters; in particular, the number of vertices used from each cherry and matching edge is divisible by three. The clusters
![]() $V_{i_1},V_{i_2},V_{i_3}$
can belong to three cherries, two cherries and one matching edge, one cherry and two matching edges, or three matching edges. We give details in the case where they are all leaves of (different) cherries, and we refer to Figure 1 for the other three cases. With (1) we find four triangles: two with a vertex in each of the other cluster of the cherry containing
$V_{i_1},V_{i_2},V_{i_3}$
can belong to three cherries, two cherries and one matching edge, one cherry and two matching edges, or three matching edges. We give details in the case where they are all leaves of (different) cherries, and we refer to Figure 1 for the other three cases. With (1) we find four triangles: two with a vertex in each of the other cluster of the cherry containing
![]() $V_{i_1}$
and the third vertex in one of the other clusters of the cherry containing
$V_{i_1}$
and the third vertex in one of the other clusters of the cherry containing
![]() $V_{i_2}$
, and other two triangles with one vertex in each of the other cluster of the cherry containing
$V_{i_2}$
, and other two triangles with one vertex in each of the other cluster of the cherry containing
![]() $V_{i_3}$
and the third vertex in the remaining cluster of the cherry containing
$V_{i_3}$
and the third vertex in the remaining cluster of the cherry containing
![]() $V_{i_2}$
. When a
$V_{i_2}$
. When a
![]() $V_{i_j}$
belongs to a matching edge of
$V_{i_j}$
belongs to a matching edge of
![]() $R'$
, we first find with (2) two triangles inside this matching edge each with one vertex in the cluster
$R'$
, we first find with (2) two triangles inside this matching edge each with one vertex in the cluster
![]() $V_{i_j}$
and the other two vertices in the other cluster of the matching edge, then we proceed as before (see Figure 1). Note that we cover three vertices of
$V_{i_j}$
and the other two vertices in the other cluster of the matching edge, then we proceed as before (see Figure 1). Note that we cover three vertices of
![]() $V_0$
using at most
$V_0$
using at most
![]() $13$
triangles, and thus to cover
$13$
triangles, and thus to cover
![]() $V' \subseteq V_0$
we use at most
$V' \subseteq V_0$
we use at most
![]() $13 |V'|/3 \le 5 |V'|$
, as claimed above. Therefore we can repeat this procedure until
$13 |V'|/3 \le 5 |V'|$
, as claimed above. Therefore we can repeat this procedure until
![]() $V'=V_0$
.
$V'=V_0$
.
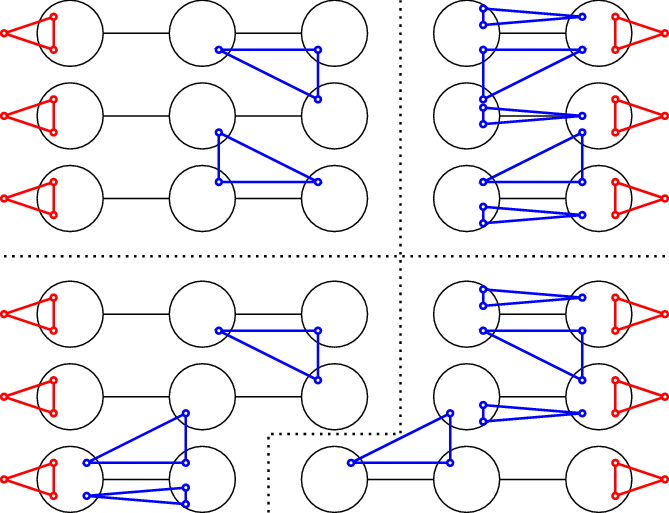
Figure 1. Embeddings of triangles for absorbing
![]() $V_0$
while using the same number of vertices from each cluster within a cherry or a matching edge. Each red triangle covers a vertex of
$V_0$
while using the same number of vertices from each cluster within a cherry or a matching edge. Each red triangle covers a vertex of
![]() $V_0$
. Each blue triangle stands for two triangles with end-points in the same clusters; we only draw one for simplicity.
$V_0$
. Each blue triangle stands for two triangles with end-points in the same clusters; we only draw one for simplicity.
Let
![]() $\mathcal{T}_1$
be the set of triangles we found above to cover
$\mathcal{T}_1$
be the set of triangles we found above to cover
![]() $V_0$
and keep the divisibility condition. We now update the regularity partition by deleting
$V_0$
and keep the divisibility condition. We now update the regularity partition by deleting
![]() $V(\mathcal{T}_1)$
from each
$V(\mathcal{T}_1)$
from each
![]() $V_i$
for
$V_i$
for
![]() $i \in [t]$
and note that for all cherries and matchings from
$i \in [t]$
and note that for all cherries and matchings from
![]() $R'$
the number of vertices in the clusters together is divisible by three. We recall that so far we removed at most
$R'$
the number of vertices in the clusters together is divisible by three. We recall that so far we removed at most
![]() $(2 \varepsilon + \delta + 2\sqrt{\delta }) n_0$
vertices from each cluster, where the first (resp. second, third) term bounds the number of vertices removed for making each pair super-regular (resp. for a later application of Lemma 4.2, for covering
$(2 \varepsilon + \delta + 2\sqrt{\delta }) n_0$
vertices from each cluster, where the first (resp. second, third) term bounds the number of vertices removed for making each pair super-regular (resp. for a later application of Lemma 4.2, for covering
![]() $V_0$
).
$V_0$
).
Balancing the partition. Now the matching edges in
![]() $R'$
are already ready for an application of Lemma 4.3, and we will not modify the corresponding clusters anymore. However, before an application of Lemma 4.2 to the cherries in
$R'$
are already ready for an application of Lemma 4.3, and we will not modify the corresponding clusters anymore. However, before an application of Lemma 4.2 to the cherries in
![]() $R'$
, we need to ensure that the ratio between their size and the size of the centre-cluster satisfies the hypotheses of the lemma. This is what we are going to do now. For
$R'$
, we need to ensure that the ratio between their size and the size of the centre-cluster satisfies the hypotheses of the lemma. This is what we are going to do now. For
![]() $i \not \in \mathcal{I}$
we denote by
$i \not \in \mathcal{I}$
we denote by
![]() $W_i$
and
$W_i$
and
![]() $U_i$
the leaf clusters of the cherry centred at
$U_i$
the leaf clusters of the cherry centred at
![]() $V_i$
. Before covering the vertices of
$V_i$
. Before covering the vertices of
![]() $V_0$
, we had
$V_0$
, we had
![]() $|W_i| = |U_i| \le (1-\delta ) |V_i|$
for
$|W_i| = |U_i| \le (1-\delta ) |V_i|$
for
![]() $i \not \in \mathcal{I}$
, which still holds as we removed the same number of vertices from each cluster of a cherry.
$i \not \in \mathcal{I}$
, which still holds as we removed the same number of vertices from each cluster of a cherry.
However we still need to guarantee the other inequality
![]() $|W_i|,|U_i| \ge (1-\delta _0) |V_i|$
. For that, we find
$|W_i|,|U_i| \ge (1-\delta _0) |V_i|$
. For that, we find
![]() $2m$
triangles with two vertices in
$2m$
triangles with two vertices in
![]() $V_i$
, of which one half has the third vertex in
$V_i$
, of which one half has the third vertex in
![]() $U_i$
and the other half in
$U_i$
and the other half in
![]() $W_i$
, where
$W_i$
, where
![]() $m$
is the smallest integer such that
$m$
is the smallest integer such that
Then after removing these
![]() $2m$
triangles, we will have precisely
$2m$
triangles, we will have precisely
![]() $(1-\delta _0)|V_i| \le |U_i| = |W_i|$
. Observe that the inequality (3) implies that
$(1-\delta _0)|V_i| \le |U_i| = |W_i|$
. Observe that the inequality (3) implies that
![]() $m \ge \frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1}$
and, as we chose the smallest such
$m \ge \frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1}$
and, as we chose the smallest such
![]() $m$
, we get
$m$
, we get
![]() $m \le \lceil \frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1} \rceil$
. Moreover, as
$m \le \lceil \frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1} \rceil$
. Moreover, as
![]() $\delta \lt \delta _0$
,
$\delta \lt \delta _0$
,
![]() $|V_i| \le n_0$
and
$|V_i| \le n_0$
and
![]() $|U_i| \ge (1-2\varepsilon -\delta -2 \sqrt{\delta } ) n_0$
, we have
$|U_i| \ge (1-2\varepsilon -\delta -2 \sqrt{\delta } ) n_0$
, we have
![]() $\frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1} \lt \frac{(1-\delta _0)-(1-2\varepsilon -\delta -2 \sqrt{\delta } )}{2}n_0 \lt 2 \sqrt{\delta }n_0$
. Therefore, for
$\frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1} \lt \frac{(1-\delta _0)-(1-2\varepsilon -\delta -2 \sqrt{\delta } )}{2}n_0 \lt 2 \sqrt{\delta }n_0$
. Therefore, for
![]() $n$
(and thus
$n$
(and thus
![]() $n_0$
) large enough,
$n_0$
) large enough,
![]() $m \le 2 \sqrt{\delta }n_0$
. We can find these at most
$m \le 2 \sqrt{\delta }n_0$
. We can find these at most
![]() $4 \sqrt{\delta } n_0$
triangles, by iteratively picking them with (2) and removing the corresponding vertices from
$4 \sqrt{\delta } n_0$
triangles, by iteratively picking them with (2) and removing the corresponding vertices from
![]() $U_i$
,
$U_i$
,
![]() $W_i$
, and
$W_i$
, and
![]() $V_i$
. Indeed, for any
$V_i$
. Indeed, for any
![]() $v \in W_i \cup U_i$
we have degree into
$v \in W_i \cup U_i$
we have degree into
![]() $V_i$
at least
$V_i$
at least
![]() $(d-3 \varepsilon - \delta -10 \sqrt{\delta })n_0 \ge dn_0/2$
, as we started from
$(d-3 \varepsilon - \delta -10 \sqrt{\delta })n_0 \ge dn_0/2$
, as we started from
![]() $(2\varepsilon,d-3\varepsilon )$
-super-regular pairs and
$(2\varepsilon,d-3\varepsilon )$
-super-regular pairs and
![]() $\delta \lt \delta ' \lt 160^{-2} d^2$
.
$\delta \lt \delta ' \lt 160^{-2} d^2$
.
Note that afterwards we still have
![]() $|U_i| \le (1-\delta )|V_i|$
as for large enough
$|U_i| \le (1-\delta )|V_i|$
as for large enough
![]() $n$
and with
$n$
and with
![]() $\delta \lt \delta _0$
we have
$\delta \lt \delta _0$
we have
![]() $m \le \lceil \frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1} \rceil \le \frac{(1-\delta )|V_i|-|U_i|}{4(1-\delta )-1}$
. Therefore, we have
$m \le \lceil \frac{(1-\delta _0)|V_i|-|U_i|}{4(1-\delta _0)-1} \rceil \le \frac{(1-\delta )|V_i|-|U_i|}{4(1-\delta )-1}$
. Therefore, we have
![]() $(1-\delta _0)|V_i| \le |U_i| = |W_i| \le (1-\delta ) |V_i|$
. Moreover with
$(1-\delta _0)|V_i| \le |U_i| = |W_i| \le (1-\delta ) |V_i|$
. Moreover with
![]() $d-3 \varepsilon -\delta -10 \sqrt{\delta } \ge d/2$
and
$d-3 \varepsilon -\delta -10 \sqrt{\delta } \ge d/2$
and
![]() $2\varepsilon \le \varepsilon '$
, we get that the pairs
$2\varepsilon \le \varepsilon '$
, we get that the pairs
![]() $(U_i,V_i)$
and
$(U_i,V_i)$
and
![]() $(W_i,V_i)$
are
$(W_i,V_i)$
are
![]() $(\varepsilon ',d/2)$
-super-regular. Let
$(\varepsilon ',d/2)$
-super-regular. Let
![]() $\mathcal{T}_2$
be the set of triangles we removed during this phase.
$\mathcal{T}_2$
be the set of triangles we removed during this phase.
Completing the triangles. Now for any
![]() $i \not \in \mathcal{I}$
, after revealing
$i \not \in \mathcal{I}$
, after revealing
![]() $G_1[V_i \cup W_i \cup U_i]$
, we a.a.s. find a triangle factor covering the vertices of
$G_1[V_i \cup W_i \cup U_i]$
, we a.a.s. find a triangle factor covering the vertices of
![]() $U_i$
,
$U_i$
,
![]() $W_i$
, and
$W_i$
, and
![]() $V_i$
by Lemma 4.2. Similarly for any matching edge
$V_i$
by Lemma 4.2. Similarly for any matching edge
![]() $ij$
of
$ij$
of
![]() $R'$
observe that
$R'$
observe that
![]() $(V_i,V_j)$
is a
$(V_i,V_j)$
is a
![]() $(\varepsilon ',d/2)$
-super-regular pair. Then after revealing
$(\varepsilon ',d/2)$
-super-regular pair. Then after revealing
![]() $G_1[V_i \cup V_j]$
, we a.a.s. find a triangle factor covering the vertices of
$G_1[V_i \cup V_j]$
, we a.a.s. find a triangle factor covering the vertices of
![]() $V_i$
and
$V_i$
and
![]() $V_j$
by Lemma 4.3. Note that we apply Lemma 4.2 and Lemma 4.3 only constantly many times and thus a.a.s. we get a triangle factor in all such applications. Let
$V_j$
by Lemma 4.3. Note that we apply Lemma 4.2 and Lemma 4.3 only constantly many times and thus a.a.s. we get a triangle factor in all such applications. Let
![]() $\mathcal{T}_3$
be the union of the triangle factors we obtain for each
$\mathcal{T}_3$
be the union of the triangle factors we obtain for each
![]() $i \not \in \mathcal{I}$
and each matching edge
$i \not \in \mathcal{I}$
and each matching edge
![]() $ij$
from
$ij$
from
![]() $R'$
. Then
$R'$
. Then
![]() $\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3$
gives
$\mathcal{T}_1 \cup \mathcal{T}_2 \cup \mathcal{T}_3$
gives
![]() $\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles in
$\lfloor n/3 \rfloor$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
7. Proof of the sublinear theorem
As outlined in the overview, we use the following two Propositions to prove Theorem 2.4.
Proposition 7.1.
For any
![]() $0\lt \gamma \lt 1/2$
there exists
$0\lt \gamma \lt 1/2$
there exists
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $(\log n)^3 \le m \le \sqrt{n}$
and any
$(\log n)^3 \le m \le \sqrt{n}$
and any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with maximum degree
$G$
with maximum degree
![]() $\Delta (G) \le \gamma n$
and minimum degree
$\Delta (G) \le \gamma n$
and minimum degree
![]() $\delta (G) \ge m$
the following holds. With
$\delta (G) \ge m$
the following holds. With
![]() $p \ge C/n$
there are a.a.s. at least
$p \ge C/n$
there are a.a.s. at least
![]() $m$
pairwise vertex-disjoint triangles in
$m$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
Proposition 7.2.
There exists
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $\sqrt{n} \le m \le n/32$
and any
$\sqrt{n} \le m \le n/32$
and any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with maximum degree
$G$
with maximum degree
![]() $\Delta (G) \le n/32$
and minimum degree
$\Delta (G) \le n/32$
and minimum degree
![]() $\delta (G) \ge m$
the following holds. With
$\delta (G) \ge m$
the following holds. With
![]() $p \ge C \log n/n$
there are a.a.s. at least
$p \ge C \log n/n$
there are a.a.s. at least
![]() $m$
pairwise vertex-disjoint triangles in
$m$
pairwise vertex-disjoint triangles in
![]() $G \cup G(n,p)$
.
$G \cup G(n,p)$
.
With this at hand we can prove Theorem 2.4.
Proof of Theorem 2.4.Let
![]() $1 \le m \le n/256$
and let
$1 \le m \le n/256$
and let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph on vertex set
$n$
-vertex graph on vertex set
![]() $V$
with minimum degree
$V$
with minimum degree
![]() $\delta (G) \ge m$
. We let
$\delta (G) \ge m$
. We let
![]() $C$
be large enough such that with
$C$
be large enough such that with
![]() $p \ge C \log n/n$
we can expose
$p \ge C \log n/n$
we can expose
![]() $G(n,p)$
in four rounds as
$G(n,p)$
in four rounds as
![]() $\bigcup _{i=1}^4 G_i$
with
$\bigcup _{i=1}^4 G_i$
with
![]() $G_i \sim G(n,C_i \log n/n)$
for
$G_i \sim G(n,C_i \log n/n)$
for
![]() $i=1,\dots,4$
such that the following hold. We let
$i=1,\dots,4$
such that the following hold. We let
![]() $C_1=1$
and observe that, by a union bound, a.a.s. for any set of vertices
$C_1=1$
and observe that, by a union bound, a.a.s. for any set of vertices
![]() $U$
of size at least
$U$
of size at least
![]() $n/256$
there is at least one edge in
$n/256$
there is at least one edge in
![]() $G_1[U]$
. Next, we let
$G_1[U]$
. Next, we let
![]() $C_2$
be large enough such that for a set of vertices
$C_2$
be large enough such that for a set of vertices
![]() $U$
of size at least
$U$
of size at least
![]() $n/2$
there are a.a.s. at least
$n/2$
there are a.a.s. at least
![]() $\log ^3 n$
pairwise vertex-disjoint triangles in
$\log ^3 n$
pairwise vertex-disjoint triangles in
![]() $G_2[U]$
[Reference Janson, Łuczak and Ruciński19, Theorem 3.29]. Finally, let
$G_2[U]$
[Reference Janson, Łuczak and Ruciński19, Theorem 3.29]. Finally, let
![]() $C_3=1$
(this is sufficient for our application of Proposition 7.1 because we do not need the
$C_3=1$
(this is sufficient for our application of Proposition 7.1 because we do not need the
![]() $\log n$
term) and
$\log n$
term) and
![]() $C_4$
be such that we can apply Proposition 7.2 with
$C_4$
be such that we can apply Proposition 7.2 with
![]() $C_4/2$
. We expose
$C_4/2$
. We expose
![]() $G_1$
already now and assume that the described property holds, while we leave
$G_1$
already now and assume that the described property holds, while we leave
![]() $G_2$
,
$G_2$
,
![]() $G_3$
, and
$G_3$
, and
![]() $G_4$
until we need them.
$G_4$
until we need them.
To apply one of the two propositions to a large subgraph
![]() $G'$
of
$G'$
of
![]() $G$
, we need
$G$
, we need
![]() $\Delta (G') \le v(G')/32$
. For this let
$\Delta (G') \le v(G')/32$
. For this let
![]() $V'$
be the set of vertices from
$V'$
be the set of vertices from
![]() $G$
of degree at least
$G$
of degree at least
![]() $n/64$
. If
$n/64$
. If
![]() $|V'|\ge m$
, then we let
$|V'|\ge m$
, then we let
![]() $V''$
be any subset of
$V''$
be any subset of
![]() $V'$
of size
$V'$
of size
![]() $m$
and we greedily find
$m$
and we greedily find
![]() $m$
pairwise vertex-disjoint triangles in
$m$
pairwise vertex-disjoint triangles in
![]() $G \cup G_1$
, each containing exactly one vertex from
$G \cup G_1$
, each containing exactly one vertex from
![]() $V''$
. Indeed, as long as we have less than
$V''$
. Indeed, as long as we have less than
![]() $m$
triangles, there is a vertex
$m$
triangles, there is a vertex
![]() $v \in V''$
not yet contained in a triangle. Then there is a set
$v \in V''$
not yet contained in a triangle. Then there is a set
![]() $U \subseteq N_G(v) \setminus V''$
of at least
$U \subseteq N_G(v) \setminus V''$
of at least
![]() $n/64-3m \ge n/256$
vertices not covered by triangles, and we can find an edge within
$n/64-3m \ge n/256$
vertices not covered by triangles, and we can find an edge within
![]() $G_1[U]$
that gives us a triangle containing
$G_1[U]$
that gives us a triangle containing
![]() $v$
and two vertices from
$v$
and two vertices from
![]() $U$
.
$U$
.
Otherwise,
![]() $|V'|\lt m$
and we remove
$|V'|\lt m$
and we remove
![]() $V'$
from
$V'$
from
![]() $G$
to obtain
$G$
to obtain
![]() $G'=G[V \setminus V']$
. Note that we have
$G'=G[V \setminus V']$
. Note that we have
![]() $v(G') = n-|V'| \ge n/2$
, minimum degree
$v(G') = n-|V'| \ge n/2$
, minimum degree
![]() $\delta (G') \ge m'= m-|V'|$
, and maximum degree
$\delta (G') \ge m'= m-|V'|$
, and maximum degree
![]() $\Delta (G') \lt n/64 \le v(G')/32$
. If
$\Delta (G') \lt n/64 \le v(G')/32$
. If
![]() $m' \lt (\log n)^3$
, then we a.a.s. find
$m' \lt (\log n)^3$
, then we a.a.s. find
![]() $m'$
pairwise vertex-disjoint triangles within
$m'$
pairwise vertex-disjoint triangles within
![]() $G_2[V(G')]$
. If
$G_2[V(G')]$
. If
![]() $(\log v(G'))^3 \le (\log n)^3 \le m' \le \sqrt{v(G')}$
, then by Proposition 7.1 and as
$(\log v(G'))^3 \le (\log n)^3 \le m' \le \sqrt{v(G')}$
, then by Proposition 7.1 and as
![]() $\log n/n= \omega (1/v(G'))$
there are a.a.s. at least
$\log n/n= \omega (1/v(G'))$
there are a.a.s. at least
![]() $m'$
pairwise vertex-disjoint triangles in
$m'$
pairwise vertex-disjoint triangles in
![]() $G' \cup G_3[V(G')]$
. Finally, if
$G' \cup G_3[V(G')]$
. Finally, if
![]() $\sqrt{v(G')} \le m' \le n/256 \le v(G')/32$
, then by Proposition 7.2 and as
$\sqrt{v(G')} \le m' \le n/256 \le v(G')/32$
, then by Proposition 7.2 and as
![]() $C_4 \log n/n \ge \frac{C_4}{2} \log v(G')/ v(G')$
, there are a.a.s. at least
$C_4 \log n/n \ge \frac{C_4}{2} \log v(G')/ v(G')$
, there are a.a.s. at least
![]() $m'$
pairwise vertex-disjoint triangles in
$m'$
pairwise vertex-disjoint triangles in
![]() $G' \cup G_4[V(G')]$
.
$G' \cup G_4[V(G')]$
.
Now, that we found
![]() $m'$
pairwise vertex-disjoint triangles, we can greedily add triangles by using the
$m'$
pairwise vertex-disjoint triangles, we can greedily add triangles by using the
![]() $m-m'$
vertices from
$m-m'$
vertices from
![]() $V'$
and an edge in their neighbourhood until we have
$V'$
and an edge in their neighbourhood until we have
![]() $m$
triangles. Analogous to above, as long as we have less than
$m$
triangles. Analogous to above, as long as we have less than
![]() $m$
triangles, for each available vertex
$m$
triangles, for each available vertex
![]() $v \in V'$
, there is a set
$v \in V'$
, there is a set
![]() $U \subseteq N_G(v) \setminus V'$
of at least
$U \subseteq N_G(v) \setminus V'$
of at least
![]() $n/256$
vertices not covered by triangles, and we find an edge within
$n/256$
vertices not covered by triangles, and we find an edge within
![]() $G_1[U]$
.
$G_1[U]$
.
It remains to prove Propositions 7.1 and 7.2. For Proposition 7.1, which deals with the cases
![]() $(\log n)^3 \le m \le \sqrt{n}$
, we first need to find many large enough vertex-disjoint stars in
$(\log n)^3 \le m \le \sqrt{n}$
, we first need to find many large enough vertex-disjoint stars in
![]() $G$
. These can be found deterministically with Lemma 7.3 below and afterwards we will show that a.a.s. at least
$G$
. These can be found deterministically with Lemma 7.3 below and afterwards we will show that a.a.s. at least
![]() $m$
of them can be completed to triangles with the help of
$m$
of them can be completed to triangles with the help of
![]() $G(n,p)$
.
$G(n,p)$
.
For any integer
![]() $g \ge 2$
, we define the star on
$g \ge 2$
, we define the star on
![]() $g+1$
vertices as the graph with one vertex of degree
$g+1$
vertices as the graph with one vertex of degree
![]() $g$
(this vertex is called the centre) and the other vertices of degree one (these vertices are called leaves). Given a star
$g$
(this vertex is called the centre) and the other vertices of degree one (these vertices are called leaves). Given a star
![]() $K$
, we denote the number of its leaves by
$K$
, we denote the number of its leaves by
![]() $g_K$
. Moreover, given a family of vertex-disjoint stars
$g_K$
. Moreover, given a family of vertex-disjoint stars
![]() $\mathcal{K}$
, we denote the set of all their centre vertices by
$\mathcal{K}$
, we denote the set of all their centre vertices by
![]() $\mathcal{K}_C$
and the set of all their leaf vertices by
$\mathcal{K}_C$
and the set of all their leaf vertices by
![]() $\mathcal{K}_L$
.
$\mathcal{K}_L$
.
Lemma 7.3.
For every
![]() $0\lt \gamma \lt 1/2$
and integer
$0\lt \gamma \lt 1/2$
and integer
![]() $s$
there exists an
$s$
there exists an
![]() $\varepsilon \gt 0$
such that for
$\varepsilon \gt 0$
such that for
![]() $n$
large enough and any
$n$
large enough and any
![]() $m$
with
$m$
with
![]() $2/\varepsilon \le m \le \sqrt{n}$
the following holds. In every
$2/\varepsilon \le m \le \sqrt{n}$
the following holds. In every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G) \ge m$
and maximum degree
$\delta (G) \ge m$
and maximum degree
![]() $\Delta (G) \le \gamma n$
, there exists a family
$\Delta (G) \le \gamma n$
, there exists a family
![]() $\mathcal{K}$
of vertex-disjoint stars in
$\mathcal{K}$
of vertex-disjoint stars in
![]() $G$
such that every
$G$
such that every
![]() $K\in{\mathcal K}$
has
$K\in{\mathcal K}$
has
![]() $g_K$
leaves with
$g_K$
leaves with
![]() $\varepsilon m \le g_K \le \varepsilon \sqrt{n}$
and
$\varepsilon m \le g_K \le \varepsilon \sqrt{n}$
and
Proof of Lemma 7.3.Given
![]() $0\lt \gamma \lt 1/2$
and an integer
$0\lt \gamma \lt 1/2$
and an integer
![]() $s$
we let
$s$
we let
![]() $\varepsilon \gt 0$
such that
$\varepsilon \gt 0$
such that
![]() $\varepsilon \le 1/(6s)$
and
$\varepsilon \le 1/(6s)$
and
![]() $\varepsilon \lt 1/2- s \gamma$
. Moreover, we let
$\varepsilon \lt 1/2- s \gamma$
. Moreover, we let
![]() $n$
be large enough for our calculations and, for simplicity, assume that
$n$
be large enough for our calculations and, for simplicity, assume that
![]() $\varepsilon \sqrt{n}$
is an integer. Then let
$\varepsilon \sqrt{n}$
is an integer. Then let
![]() $2/\varepsilon \le m \le \sqrt{n}$
and
$2/\varepsilon \le m \le \sqrt{n}$
and
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph on vertex set
$n$
-vertex graph on vertex set
![]() $V$
with
$V$
with
![]() $\delta (G) \ge m$
and
$\delta (G) \ge m$
and
![]() $\Delta (G) \le \gamma n$
.
$\Delta (G) \le \gamma n$
.
Let
![]() $\mathcal{K}$
be a family of vertex-disjoint stars in
$\mathcal{K}$
be a family of vertex-disjoint stars in
![]() $G$
with
$G$
with
![]() $\varepsilon m \le g_K \le \varepsilon \sqrt{n}$
for all
$\varepsilon m \le g_K \le \varepsilon \sqrt{n}$
for all
![]() $K \in \mathcal{K}$
, that maximizes the sum
$K \in \mathcal{K}$
, that maximizes the sum
among all such families. Note that each star in
![]() $\mathcal{K}$
has at least
$\mathcal{K}$
has at least
![]() $2$
leaves because
$2$
leaves because
![]() $g_K \ge \varepsilon m$
and
$g_K \ge \varepsilon m$
and
![]() $m \ge 2/\varepsilon$
.
$m \ge 2/\varepsilon$
.
If the sum in (4) is bigger than
![]() $s \varepsilon ^2 n m$
we are done. So we assume the family
$s \varepsilon ^2 n m$
we are done. So we assume the family
![]() $\mathcal{K}$
satisfies
$\mathcal{K}$
satisfies
We are going to prove that then there exists a vertex of degree larger than
![]() $\gamma n$
, contradicting our assumption on the maximum degree.
$\gamma n$
, contradicting our assumption on the maximum degree.
For this we split
![]() $\mathcal{K}$
into two subfamilies
$\mathcal{K}$
into two subfamilies
and we let
![]() $R$
be the set of vertices not covered by the stars in
$R$
be the set of vertices not covered by the stars in
![]() $\mathcal{K}$
, that is
$\mathcal{K}$
, that is
![]() $R=V(G) \setminus (\mathcal{H}_C \cup \mathcal{H}_L \cup \mathcal{M}_C \cup \mathcal{M}_L)$
, where
$R=V(G) \setminus (\mathcal{H}_C \cup \mathcal{H}_L \cup \mathcal{M}_C \cup \mathcal{M}_L)$
, where
![]() $\mathcal{H}_C$
,
$\mathcal{H}_C$
,
![]() $\mathcal{H}_L$
,
$\mathcal{H}_L$
,
![]() $\mathcal{M}_C$
, and
$\mathcal{M}_C$
, and
![]() $\mathcal{M}_L$
are obtained from
$\mathcal{M}_L$
are obtained from
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $\mathcal{H}$
as defined above.
$\mathcal{H}$
as defined above.
For all stars
![]() $K \in \mathcal{H}$
we have
$K \in \mathcal{H}$
we have
![]() $g_K^2=\varepsilon ^2 n$
. From (5), we get that the subfamily
$g_K^2=\varepsilon ^2 n$
. From (5), we get that the subfamily
![]() $\mathcal{H}$
contains at most
$\mathcal{H}$
contains at most
![]() $sm$
stars and hence
$sm$
stars and hence
because
![]() $m \le \sqrt{n}$
.
$m \le \sqrt{n}$
.
As each star in
![]() $\mathcal{M}$
has at least
$\mathcal{M}$
has at least
![]() $\varepsilon m$
leaves, we have
$\varepsilon m$
leaves, we have
![]() $\sum _{K \in \mathcal{M}} g_K \ge |\mathcal{M}| \varepsilon m$
. Using the Cauchy-Schwarz inequality, we then get
$\sum _{K \in \mathcal{M}} g_K \ge |\mathcal{M}| \varepsilon m$
. Using the Cauchy-Schwarz inequality, we then get
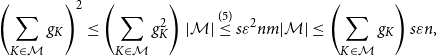 \begin{equation*}\left (\sum _{K \in \mathcal {M}} g_K\right )^2 \le \left (\sum _{K \in \mathcal {M}} g_K^2 \right ) |\mathcal {M}| \stackrel {(5)}{\leq } s \varepsilon ^2 nm |\mathcal {M}| \le \left (\sum _{K \in \mathcal {M}} g_K\right ) s \varepsilon n, \end{equation*}
\begin{equation*}\left (\sum _{K \in \mathcal {M}} g_K\right )^2 \le \left (\sum _{K \in \mathcal {M}} g_K^2 \right ) |\mathcal {M}| \stackrel {(5)}{\leq } s \varepsilon ^2 nm |\mathcal {M}| \le \left (\sum _{K \in \mathcal {M}} g_K\right ) s \varepsilon n, \end{equation*}
which implies
Therefore,
![]() $|\mathcal{M}_C| \le |\mathcal{M}_L|/2 \le s \varepsilon n/2$
since each star has at least
$|\mathcal{M}_C| \le |\mathcal{M}_L|/2 \le s \varepsilon n/2$
since each star has at least
![]() $2$
leaves.
$2$
leaves.
These bounds on
![]() $\mathcal{M}_L$
and
$\mathcal{M}_L$
and
![]() $\mathcal{M}_C$
together with (6) immediately imply that
$\mathcal{M}_C$
together with (6) immediately imply that
![]() $|R| \ge (1-3 s \varepsilon ) n \ge n/2$
. We are going to show that there are many edges between
$|R| \ge (1-3 s \varepsilon ) n \ge n/2$
. We are going to show that there are many edges between
![]() $R$
and
$R$
and
![]() $\mathcal{H}_C$
and from that we derive the existence of a high degree vertex, giving the desired contradiction.
$\mathcal{H}_C$
and from that we derive the existence of a high degree vertex, giving the desired contradiction.
A vertex in
![]() $R$
cannot have at least
$R$
cannot have at least
![]() $\varepsilon m$
neighbours inside
$\varepsilon m$
neighbours inside
![]() $R$
, because otherwise we could create a new star and increase the sum in (4). Therefore,
$R$
, because otherwise we could create a new star and increase the sum in (4). Therefore,
![]() $e(R) \lt |R| \varepsilon m/2$
. We also have
$e(R) \lt |R| \varepsilon m/2$
. We also have
![]() $e(R,\mathcal{M}_C)=0$
since otherwise we could add an edge to one of the existing stars in
$e(R,\mathcal{M}_C)=0$
since otherwise we could add an edge to one of the existing stars in
![]() $\mathcal{K}$
increasing the sum in (4) (recall that stars in
$\mathcal{K}$
increasing the sum in (4) (recall that stars in
![]() $\mathcal{M}$
have less than
$\mathcal{M}$
have less than
![]() $\varepsilon \sqrt{n}$
leaves).
$\varepsilon \sqrt{n}$
leaves).
Given a leaf
![]() $v \in \mathcal{M}_L$
that belongs to a star
$v \in \mathcal{M}_L$
that belongs to a star
![]() $K$
with
$K$
with
![]() $g_K$
leaves, we must have
$g_K$
leaves, we must have
![]() $\deg (v,R) \lt g_K+1$
. Otherwise, we could take
$\deg (v,R) \lt g_K+1$
. Otherwise, we could take
![]() $V' \subseteq N_R(v)$
of size
$V' \subseteq N_R(v)$
of size
![]() $|V'|=g_k+1 \le \varepsilon \sqrt{n}$
and create a new family of vertex-disjoint stars, given by
$|V'|=g_k+1 \le \varepsilon \sqrt{n}$
and create a new family of vertex-disjoint stars, given by
![]() $\mathcal{K} \setminus \{K\}$
and the star on
$\mathcal{K} \setminus \{K\}$
and the star on
![]() $v \cup V'$
, to increase the sum in (4). Therefore,
$v \cup V'$
, to increase the sum in (4). Therefore,
Similarly, given
![]() $v \in \mathcal{H}_L$
, we must have
$v \in \mathcal{H}_L$
, we must have
![]() $\deg (v,R) \lt \varepsilon \sqrt{n}$
. Otherwise, we could take
$\deg (v,R) \lt \varepsilon \sqrt{n}$
. Otherwise, we could take
![]() $V' \subseteq N_R(v)$
of size
$V' \subseteq N_R(v)$
of size
![]() $|V'|=\varepsilon \sqrt{n}$
and create a new family of vertex-disjoint stars, given by
$|V'|=\varepsilon \sqrt{n}$
and create a new family of vertex-disjoint stars, given by
![]() $\mathcal{K} \setminus \{K\}$
, the star
$\mathcal{K} \setminus \{K\}$
, the star
![]() $K \setminus \left \{v\right \}$
, and the star on
$K \setminus \left \{v\right \}$
, and the star on
![]() $v \cup V'$
, to increase the sum in (4). Therefore,
$v \cup V'$
, to increase the sum in (4). Therefore,
![]() $e(R,\mathcal{H}_L) \le |\mathcal{H}_L| \varepsilon \sqrt{n} \le s \varepsilon ^2 n m$
by (6).
$e(R,\mathcal{H}_L) \le |\mathcal{H}_L| \varepsilon \sqrt{n} \le s \varepsilon ^2 n m$
by (6).
On the other hand,
![]() $\delta (G) \ge m$
implies
$\delta (G) \ge m$
implies
![]() $e(R,V) \ge m |R|$
, where the edges inside of
$e(R,V) \ge m |R|$
, where the edges inside of
![]() $R$
are counted twice. Then we can lower bound the number of edges between
$R$
are counted twice. Then we can lower bound the number of edges between
![]() $R$
and
$R$
and
![]() $\mathcal{H}_C$
by
$\mathcal{H}_C$
by
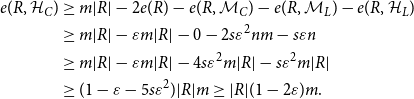 \begin{align*} e(R,\mathcal{H}_C) & \ge m |R|-2 e(R)-e(R,\mathcal{M}_C)-e(R,\mathcal{M}_L)-e(R,\mathcal{H}_L) \\ &\ge m |R| - \varepsilon m |R|- 0 - 2 s \varepsilon ^2 n m - s \varepsilon n \\ &\ge m |R| - \varepsilon m |R| - 4 s \varepsilon ^2 m |R| - s \varepsilon ^2 m |R| \\ &\ge (1-\varepsilon - 5 s \varepsilon ^2) |R| m \ge |R|(1-2 \varepsilon )m. \end{align*}
\begin{align*} e(R,\mathcal{H}_C) & \ge m |R|-2 e(R)-e(R,\mathcal{M}_C)-e(R,\mathcal{M}_L)-e(R,\mathcal{H}_L) \\ &\ge m |R| - \varepsilon m |R|- 0 - 2 s \varepsilon ^2 n m - s \varepsilon n \\ &\ge m |R| - \varepsilon m |R| - 4 s \varepsilon ^2 m |R| - s \varepsilon ^2 m |R| \\ &\ge (1-\varepsilon - 5 s \varepsilon ^2) |R| m \ge |R|(1-2 \varepsilon )m. \end{align*}
where we used the bounds on
![]() $e(R)$
,
$e(R)$
,
![]() $e(R,\mathcal{M}_C)$
,
$e(R,\mathcal{M}_C)$
,
![]() $e(R,\mathcal{M}_L)$
, and
$e(R,\mathcal{M}_L)$
, and
![]() $e(R,\mathcal{H}_L)$
we found above, together with
$e(R,\mathcal{H}_L)$
we found above, together with
![]() $|R| \ge n/2$
,
$|R| \ge n/2$
,
![]() $\varepsilon m \ge 2$
and the choice of
$\varepsilon m \ge 2$
and the choice of
![]() $\varepsilon \lt 1/(6s)$
. In particular, as
$\varepsilon \lt 1/(6s)$
. In particular, as
![]() $|\mathcal{H}_C| \le sm$
and using
$|\mathcal{H}_C| \le sm$
and using
![]() $\varepsilon \lt 1/2- s \gamma$
, and
$\varepsilon \lt 1/2- s \gamma$
, and
![]() $|R| \gt n/2$
, there exists a vertex
$|R| \gt n/2$
, there exists a vertex
![]() $v \in \mathcal{H}_C$
of degree
$v \in \mathcal{H}_C$
of degree
This contradicts the maximum degree of
![]() $G$
.
$G$
.
Proof of Proposition 7.1.Let
![]() $n$
be sufficiently large for the following arguments. With
$n$
be sufficiently large for the following arguments. With
![]() $0\lt \gamma \lt 1/2$
let
$0\lt \gamma \lt 1/2$
let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with maximum degree
$n$
-vertex graph with maximum degree
![]() $\Delta (G) \le \gamma n$
and minimum degree
$\Delta (G) \le \gamma n$
and minimum degree
![]() $\delta (G) \ge m$
. With
$\delta (G) \ge m$
. With
![]() $(\log n)^3 \le m \le \sqrt{n}$
, we first find many vertex-disjoint stars in
$(\log n)^3 \le m \le \sqrt{n}$
, we first find many vertex-disjoint stars in
![]() $G$
and then complete at least
$G$
and then complete at least
![]() $m$
of them to triangles with the help of
$m$
of them to triangles with the help of
![]() $G(n,p)$
. We apply Lemma 7.3 with
$G(n,p)$
. We apply Lemma 7.3 with
![]() $\gamma$
and
$\gamma$
and
![]() $s=8$
to get
$s=8$
to get
![]() $0\lt \varepsilon \lt 1/2$
and, as
$0\lt \varepsilon \lt 1/2$
and, as
![]() $n$
is large enough and
$n$
is large enough and
![]() $m \ge 2/\varepsilon$
, we get a family
$m \ge 2/\varepsilon$
, we get a family
![]() $\mathcal{K}$
of vertex-disjoint stars on
$\mathcal{K}$
of vertex-disjoint stars on
![]() $V(G)$
such that
$V(G)$
such that
![]() $\varepsilon m \le g_K \le \varepsilon \sqrt{n}$
for
$\varepsilon m \le g_K \le \varepsilon \sqrt{n}$
for
![]() $K \in \mathcal{K}$
and
$K \in \mathcal{K}$
and
![]() $\sum _{K \in \mathcal{K}} g_K^2 \ge 8 \varepsilon ^2 n m$
.
$\sum _{K \in \mathcal{K}} g_K^2 \ge 8 \varepsilon ^2 n m$
.
As we have stars of different sizes, we split
![]() $\mathcal{K}$
into
$\mathcal{K}$
into
![]() $t=\lceil \log (\sqrt{n}/m)/\log 2 \rceil +1$
subfamilies
$t=\lceil \log (\sqrt{n}/m)/\log 2 \rceil +1$
subfamilies
and set
![]() $k_i =|\mathcal{K}_i|$
.
$k_i =|\mathcal{K}_i|$
.
By deleting leaves, we may assume that all stars in
![]() $\mathcal{K}_i$
have exactly
$\mathcal{K}_i$
have exactly
![]() $\lceil 2^{i-1} \varepsilon m \rceil$
leaves. Denote by
$\lceil 2^{i-1} \varepsilon m \rceil$
leaves. Denote by
![]() $\mathcal{I}$
the set of indices
$\mathcal{I}$
the set of indices
![]() $i \in [t]$
such that
$i \in [t]$
such that
![]() $k_i \left ( 2^{i-1} \varepsilon m \right )^2 \ge \varepsilon ^2 n m/t$
. Next we prove that
$k_i \left ( 2^{i-1} \varepsilon m \right )^2 \ge \varepsilon ^2 n m/t$
. Next we prove that
![]() $\sum _{i \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2 \ge \varepsilon ^2 nm.$
$\sum _{i \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2 \ge \varepsilon ^2 nm.$
Observe first that
![]() $\sum _{i \not \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2 \le t (\varepsilon ^2 nm/t)=\varepsilon ^2 nm$
. It follows that
$\sum _{i \not \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2 \le t (\varepsilon ^2 nm/t)=\varepsilon ^2 nm$
. It follows that
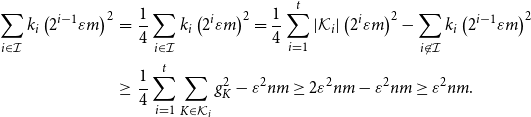 \begin{eqnarray*} \sum _{i \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2 &=& \frac{1}{4} \sum _{i \in \mathcal{I}} k_i \left ( 2^i \varepsilon m \right )^2 = \frac{1}{4} \sum _{i=1}^t |\mathcal{K}_i| \left ( 2^i \varepsilon m \right )^2 -\sum _{i \not \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2\\ &\ge &\frac{1}{4} \sum _{i=1}^t \sum _{K\in \mathcal{K}_i} g_K^2 - \varepsilon ^2 nm\ge 2 \varepsilon ^2 nm - \varepsilon ^2 nm \ge \varepsilon ^2 nm. \end{eqnarray*}
\begin{eqnarray*} \sum _{i \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2 &=& \frac{1}{4} \sum _{i \in \mathcal{I}} k_i \left ( 2^i \varepsilon m \right )^2 = \frac{1}{4} \sum _{i=1}^t |\mathcal{K}_i| \left ( 2^i \varepsilon m \right )^2 -\sum _{i \not \in \mathcal{I}} k_i \left ( 2^{i-1} \varepsilon m \right )^2\\ &\ge &\frac{1}{4} \sum _{i=1}^t \sum _{K\in \mathcal{K}_i} g_K^2 - \varepsilon ^2 nm\ge 2 \varepsilon ^2 nm - \varepsilon ^2 nm \ge \varepsilon ^2 nm. \end{eqnarray*}
Now we reveal random edges on
![]() $V(G)$
with probability
$V(G)$
with probability
![]() $p \ge C/n$
where
$p \ge C/n$
where
![]() $C$
is large enough for the Chernoff bounds and inequalities below. We shall show that this allows us to find at least
$C$
is large enough for the Chernoff bounds and inequalities below. We shall show that this allows us to find at least
![]() $m$
triangles a.a.s.. Indeed, for each
$m$
triangles a.a.s.. Indeed, for each
![]() $i \in \mathcal{I}$
, we find many pairwise vertex-disjoint triangles in
$i \in \mathcal{I}$
, we find many pairwise vertex-disjoint triangles in
![]() $\mathcal{K}_i$
using random edges.
$\mathcal{K}_i$
using random edges.
Claim 7.4.
For any
![]() $i \in \mathcal{I}$
, after revealing edges of
$i \in \mathcal{I}$
, after revealing edges of
![]() $G(n,p)$
with
$G(n,p)$
with
![]() $p \ge C/n$
, we have with probability at least
$p \ge C/n$
, we have with probability at least
![]() $1-1/n$
at least
$1-1/n$
at least
![]() $k_i (2^{i-1}m)^2/ n$
pairwise vertex-disjoint triangles within
$k_i (2^{i-1}m)^2/ n$
pairwise vertex-disjoint triangles within
![]() $(G \cup G(n,p))[\cup _{K \in \mathcal{K}_i} V(K)]$
.
$(G \cup G(n,p))[\cup _{K \in \mathcal{K}_i} V(K)]$
.
Having this claim and since
![]() $|\mathcal{I}| \le t =o (n)$
, with a union bound over
$|\mathcal{I}| \le t =o (n)$
, with a union bound over
![]() $i \in \mathcal{I}$
, there are a.a.s. at least
$i \in \mathcal{I}$
, there are a.a.s. at least
pairwise vertex-disjoint triangles in
![]() $G\cup G(n,p)$
. It remains to prove Claim 7.4.
$G\cup G(n,p)$
. It remains to prove Claim 7.4.
Proof of Claim 7.4.Fix
![]() $i \in \mathcal{I}$
and let
$i \in \mathcal{I}$
and let
![]() $k=k_i$
and
$k=k_i$
and
![]() $g = \lceil 2^{i-1} \varepsilon m \rceil$
. We reveal random edges with probability
$g = \lceil 2^{i-1} \varepsilon m \rceil$
. We reveal random edges with probability
![]() $p$
within each set of leaves of the
$p$
within each set of leaves of the
![]() $k$
stars in
$k$
stars in
![]() $\mathcal{K}_i$
. We recall that these
$\mathcal{K}_i$
. We recall that these
![]() $k$
sets are pairwise disjoint and each has size
$k$
sets are pairwise disjoint and each has size
![]() $g$
. Let
$g$
. Let
![]() $X_j$
be the indicator variable of the event that the
$X_j$
be the indicator variable of the event that the
![]() $j$
th of these sets contains at least one edge for
$j$
th of these sets contains at least one edge for
![]() $1 \le j \le k$
, and set
$1 \le j \le k$
, and set
![]() $X = \sum _{j=1}^kX_i$
. Then
$X = \sum _{j=1}^kX_i$
. Then
![]() $\mathbb{P}[X_j=1]=1-(1-p)^{\binom{g}{2}}$
and
$\mathbb{P}[X_j=1]=1-(1-p)^{\binom{g}{2}}$
and
![]() $\mathbb{E}[X] = k \left ( 1-(1-p)^{\binom{g}{2}} \right )$
. We have that
$\mathbb{E}[X] = k \left ( 1-(1-p)^{\binom{g}{2}} \right )$
. We have that
![]() $\mathbb{E}[X] \ge 2 k g^2/(\varepsilon ^2 n)$
. Indeed,
$\mathbb{E}[X] \ge 2 k g^2/(\varepsilon ^2 n)$
. Indeed,
and the later holds for large enough
![]() $C$
and
$C$
and
![]() $n$
using the inequality
$n$
using the inequality
![]() $1-x\le e^{-x}\le 1-\frac{x}{2}$
valid for
$1-x\le e^{-x}\le 1-\frac{x}{2}$
valid for
![]() $x\lt 3/2$
.
$x\lt 3/2$
.
From Chernoff’s inequality (Lemma 3.1) and from the fact that
![]() $k g^2/(\varepsilon ^2 n) \ge m/t$
by the definition of
$k g^2/(\varepsilon ^2 n) \ge m/t$
by the definition of
![]() $\mathcal{I}$
, it follows that with probability at most
$\mathcal{I}$
, it follows that with probability at most
there are less than
![]() $kg^2/(\varepsilon ^2 n)$
triangles, where the last inequality holds as
$kg^2/(\varepsilon ^2 n)$
triangles, where the last inequality holds as
![]() $t \le \log n$
,
$t \le \log n$
,
![]() $m \ge (\log n)^3$
, and
$m \ge (\log n)^3$
, and
![]() $n$
is large enough.
$n$
is large enough.
Proof of Proposition 7.2.Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with maximum degree
$n$
-vertex graph with maximum degree
![]() $\Delta (G) \le n/32$
and minimum degree
$\Delta (G) \le n/32$
and minimum degree
![]() $\delta (G) \ge m$
. With
$\delta (G) \ge m$
. With
![]() $\sqrt{n} \le m \le n/32$
, we cannot hope to find sufficiently many large enough vertex-disjoint stars (as we did in the proof of Proposition 7.1). Instead we apply a greedy strategy, using that a.a.s. every vertex of
$\sqrt{n} \le m \le n/32$
, we cannot hope to find sufficiently many large enough vertex-disjoint stars (as we did in the proof of Proposition 7.1). Instead we apply a greedy strategy, using that a.a.s. every vertex of
![]() $G$
has random edges in its neighbourhood. We can greedily obtain a spanning bipartite subgraph
$G$
has random edges in its neighbourhood. We can greedily obtain a spanning bipartite subgraph
![]() $G' \subseteq G$
of minimum degree
$G' \subseteq G$
of minimum degree
![]() $\delta (G') \ge m/2$
by taking a partition of
$\delta (G') \ge m/2$
by taking a partition of
![]() $V(G)$
into sets
$V(G)$
into sets
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
![]() $e_G(A,B)$
is maximised and letting
$e_G(A,B)$
is maximised and letting
![]() $G'=G[A,B]$
. Indeed, a vertex of degree less than
$G'=G[A,B]$
. Indeed, a vertex of degree less than
![]() $m/2$
can be moved to the other class to increase
$m/2$
can be moved to the other class to increase
![]() $e_G(A,B)$
. W.l.o.g. we assume
$e_G(A,B)$
. W.l.o.g. we assume
![]() $|B|\ge n/2\ge |A|$
. Moreover, we have
$|B|\ge n/2\ge |A|$
. Moreover, we have
![]() $|A| \ge 8m$
, as otherwise with
$|A| \ge 8m$
, as otherwise with
![]() $e(A,B) \ge nm/4$
there is a vertex of degree larger than
$e(A,B) \ge nm/4$
there is a vertex of degree larger than
![]() $n/32$
, a contradiction.
$n/32$
, a contradiction.
Claim 7.5.
For every
![]() $A' \subseteq A$
,
$A' \subseteq A$
,
![]() $B' \subseteq B$
with
$B' \subseteq B$
with
![]() $|A'| \lt 2m$
,
$|A'| \lt 2m$
,
![]() $|B'| \ge n/4$
we have
$|B'| \ge n/4$
we have
![]() $e(A \setminus A',B') \ge n m/16$
.
$e(A \setminus A',B') \ge n m/16$
.
Proof. If
![]() $e(A \setminus A',B') \lt n m/16$
, it follows from
$e(A \setminus A',B') \lt n m/16$
, it follows from
![]() $e(A,B') \ge |B'| m/2\ge nm/8$
that we have
$e(A,B') \ge |B'| m/2\ge nm/8$
that we have
![]() $e(A',B') \ge n m/16$
. Since
$e(A',B') \ge n m/16$
. Since
![]() $|A'| \lt 2m$
, there must be a vertex of degree at least
$|A'| \lt 2m$
, there must be a vertex of degree at least
![]() $n/32$
in
$n/32$
in
![]() $A'$
, a contradiction.
$A'$
, a contradiction.
From this claim, it follows that there are many vertices of high degree in
![]() $A \setminus A'$
.
$A \setminus A'$
.
Claim 7.6.
Suppose that
![]() $A' \subseteq A$
,
$A' \subseteq A$
,
![]() $B' \subseteq B$
with
$B' \subseteq B$
with
![]() $|A'| \lt 2m$
,
$|A'| \lt 2m$
,
![]() $|B'| \ge n/4$
. Let
$|B'| \ge n/4$
. Let
![]() $ A^* = \{ v \in A \setminus A' \,\colon \, \deg (v,B') \ge m/16 \}$
. Then
$ A^* = \{ v \in A \setminus A' \,\colon \, \deg (v,B') \ge m/16 \}$
. Then
![]() $|A^*| \ge m.$
$|A^*| \ge m.$
Proof. We have
![]() $|A^*| n/32 + |A| m/16 \ge e(A^*,B') +e(A \setminus (A'\cup A^*),B') = e(A \setminus A',B') \ge nm/16$
, where the last inequality uses Claim 7.5. Since
$|A^*| n/32 + |A| m/16 \ge e(A^*,B') +e(A \setminus (A'\cup A^*),B') = e(A \setminus A',B') \ge nm/16$
, where the last inequality uses Claim 7.5. Since
![]() $|A| \le n/2$
, we get
$|A| \le n/2$
, we get
Let
![]() $s=\lceil \frac{2n}{m} \rceil$
and
$s=\lceil \frac{2n}{m} \rceil$
and
![]() $t= \lceil \frac{m^2}{2n} \rceil$
. We will now iteratively construct our
$t= \lceil \frac{m^2}{2n} \rceil$
. We will now iteratively construct our
![]() $m$
triangles in
$m$
triangles in
![]() $t$
rounds of
$t$
rounds of
![]() $s$
triangles each. In each round, we will reveal
$s$
triangles each. In each round, we will reveal
![]() $G(n,q)$
with
$G(n,q)$
with
![]() $q = \frac{C \log n}{m^{2}}$
, where
$q = \frac{C \log n}{m^{2}}$
, where
![]() $C$
is large enough for the Chernoff bound below. For the start, we set
$C$
is large enough for the Chernoff bound below. For the start, we set
![]() $A'=B_0=\emptyset$
.
$A'=B_0=\emptyset$
.
Let
![]() $i=1,\dots,t$
, suppose that before the
$i=1,\dots,t$
, suppose that before the
![]() $i$
th round we have
$i$
th round we have
and
![]() $|B_0|=(i-1)(2s) \lt 3m$
, and note this is true for
$|B_0|=(i-1)(2s) \lt 3m$
, and note this is true for
![]() $i=1$
. In the
$i=1$
. In the
![]() $i$
th round, we pick vertices
$i$
th round, we pick vertices
![]() $v_1,\dots,v_s \in A \setminus A'$
and pairwise disjoint sets
$v_1,\dots,v_s \in A \setminus A'$
and pairwise disjoint sets
![]() $B_1,\dots,B_s \subseteq B \setminus B_0$
, each of size
$B_1,\dots,B_s \subseteq B \setminus B_0$
, each of size
![]() $\lceil m/16 \rceil$
, such that
$\lceil m/16 \rceil$
, such that
![]() $B_j \subseteq N_{G'}(v_j)$
for each
$B_j \subseteq N_{G'}(v_j)$
for each
![]() $j=1,\dots,s$
. We can do this greedily, where for
$j=1,\dots,s$
. We can do this greedily, where for
![]() $j=1,\dots,s$
we set
$j=1,\dots,s$
we set
![]() $B'=B \setminus (B_0 \cup B_1 \cup \dots \cup B_{j-1})$
and apply Claim 7.6 to obtain a vertex
$B'=B \setminus (B_0 \cup B_1 \cup \dots \cup B_{j-1})$
and apply Claim 7.6 to obtain a vertex
![]() $v_j \in A \setminus A'$
together with a set
$v_j \in A \setminus A'$
together with a set
![]() $B_j \subseteq B'$
of
$B_j \subseteq B'$
of
![]() $\lceil m/16 \rceil$
neighbours of
$\lceil m/16 \rceil$
neighbours of
![]() $v_j$
. We can do this as
$v_j$
. We can do this as
![]() $|A'| \lt 2m$
and
$|A'| \lt 2m$
and
![]() $|B'| \ge n/2 - s \lceil m/16 \rceil - |B_0| \ge n/4$
as
$|B'| \ge n/2 - s \lceil m/16 \rceil - |B_0| \ge n/4$
as
![]() $m\le n/32$
.
$m\le n/32$
.
Now we reveal additional edges at random with probability
![]() $q$
. Then with probability at least
$q$
. Then with probability at least
![]() $1-1/n^2$
, we have at least one edge in each set
$1-1/n^2$
, we have at least one edge in each set
![]() $B_1, \dots, B_s$
. Indeed the probability that there is no edge in a set
$B_1, \dots, B_s$
. Indeed the probability that there is no edge in a set
![]() $B_i$
is at most
$B_i$
is at most
![]() $(1-q)^{\binom{|B_i|}{2}} \le \exp (-C \tfrac{\log n}{m} \binom{\lceil m/16 \rceil }{2}) \le n^{-3}$
as
$(1-q)^{\binom{|B_i|}{2}} \le \exp (-C \tfrac{\log n}{m} \binom{\lceil m/16 \rceil }{2}) \le n^{-3}$
as
![]() $C$
is large enough. Therefore, the probability that there is a set without any edge is at most
$C$
is large enough. Therefore, the probability that there is a set without any edge is at most
![]() $s n^{-3} \le n^{-2}$
by a union bound. We fix an arbitrary edge from each
$s n^{-3} \le n^{-2}$
by a union bound. We fix an arbitrary edge from each
![]() $B_i$
and together with
$B_i$
and together with
![]() $v_1,\dots,v_s$
this gives us
$v_1,\dots,v_s$
this gives us
![]() $s$
triangles. We add the vertices
$s$
triangles. We add the vertices
![]() $v_1,\dots,v_s$
to
$v_1,\dots,v_s$
to
![]() $A'$
and the vertices of the edges that we chose to
$A'$
and the vertices of the edges that we chose to
![]() $B_0$
. Notice that
$B_0$
. Notice that
![]() $|A'|=is$
and
$|A'|=is$
and
![]() $|B'|=i(2s)$
, as required at the beginning of next round.
$|B'|=i(2s)$
, as required at the beginning of next round.
We can repeat the above
![]() $t$
times because with
$t$
times because with
![]() $m \ge \sqrt{n}$
we get
$m \ge \sqrt{n}$
we get
![]() $t q \le \frac{C \log n}{n} = p$
. By a union bound over the
$t q \le \frac{C \log n}{n} = p$
. By a union bound over the
![]() $t=\lceil \frac{m^2}{2n} \rceil \le n$
rounds, we get that we succeed a.a.s. and find
$t=\lceil \frac{m^2}{2n} \rceil \le n$
rounds, we get that we succeed a.a.s. and find
![]() $t s \ge m$
triangles.
$t s \ge m$
triangles.
8. Proof of the auxiliary lemmas
In this section, we prove Lemmas 4.1, 4.2, and 4.3. For each of them, we first give an overview of the strategy and then a full proof.
8.1 Proof of Lemmas 4.1 and 4.2
We describe the general setup of both Lemmas 4.1 and 4.2. Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $U \cup V \cup W$
with
$U \cup V \cup W$
with
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
being super-regular with respect to
$(V,W)$
being super-regular with respect to
![]() $G$
. We will find all/most triangles, respectively, with one vertex in each of the sets
$G$
. We will find all/most triangles, respectively, with one vertex in each of the sets
![]() $U$
,
$U$
,
![]() $V$
, and
$V$
, and
![]() $W$
, with the edges between
$W$
, with the edges between
![]() $U$
and
$U$
and
![]() $W$
coming from the random graph. To find these edges, we consider a random matching
$W$
coming from the random graph. To find these edges, we consider a random matching
![]() $M$
in
$M$
in
![]() $G(U,W,p)$
such that each matching edge is contained in many triangles with the third vertex from
$G(U,W,p)$
such that each matching edge is contained in many triangles with the third vertex from
![]() $V$
. As we later want to match edges from
$V$
. As we later want to match edges from
![]() $M$
to vertices from
$M$
to vertices from
![]() $V$
, in order to get triangles, we consider the following bipartite auxiliary graph. Given a matching
$V$
, in order to get triangles, we consider the following bipartite auxiliary graph. Given a matching
![]() $M$
between
$M$
between
![]() $U$
and
$U$
and
![]() $W$
, the vertex set of the graph
$W$
, the vertex set of the graph
![]() $H_G(M,V)$
consists of
$H_G(M,V)$
consists of
![]() $M$
and
$M$
and
![]() $V$
and there is an edge between
$V$
and there is an edge between
![]() $m \in M$
and
$m \in M$
and
![]() $v \in V$
if and only if the vertices of
$v \in V$
if and only if the vertices of
![]() $m$
are incident to
$m$
are incident to
![]() $v$
in
$v$
in
![]() $G$
. The lemma below states that with
$G$
. The lemma below states that with
![]() $ p \ge C/n$
, we can a.a.s. find a large matching
$ p \ge C/n$
, we can a.a.s. find a large matching
![]() $M$
such that additionally
$M$
such that additionally
![]() $(M,V)$
gives a super-regular pair in
$(M,V)$
gives a super-regular pair in
![]() $H_G(M,V)$
. Observe that a matching within
$H_G(M,V)$
. Observe that a matching within
![]() $H_G(M,V)$
induces pairwise vertex-disjoint triangles in
$H_G(M,V)$
induces pairwise vertex-disjoint triangles in
![]() $G \cup G(U,W,p)$
.
$G \cup G(U,W,p)$
.
Lemma 8.1.
For any
![]() $0 \lt d,\delta,\varepsilon ' \lt 1$
with
$0 \lt d,\delta,\varepsilon ' \lt 1$
with
![]() $2\delta \le d$
there exist
$2\delta \le d$
there exist
![]() $\varepsilon,C\gt 0$
such that the following holds. Let
$\varepsilon,C\gt 0$
such that the following holds. Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $U \cup V \cup W$
, with
$U \cup V \cup W$
, with
![]() $|V|=n$
and
$|V|=n$
and
![]() $(1-1/2)n \le |U|=|W| \le (1 + 1/2) n$
, such that
$(1-1/2)n \le |U|=|W| \le (1 + 1/2) n$
, such that
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
are
$(V,W)$
are
![]() $(\varepsilon,d)$
-super-regular pairs with respect to
$(\varepsilon,d)$
-super-regular pairs with respect to
![]() $G$
. Further, let
$G$
. Further, let
![]() $G(U,W,p)$
be a random graph with
$G(U,W,p)$
be a random graph with
![]() $p \ge C/n$
. Then a.a.s. there exists a matching
$p \ge C/n$
. Then a.a.s. there exists a matching
![]() $M \subseteq G(U,W,p)$
of size
$M \subseteq G(U,W,p)$
of size
![]() $|M| = (1-\delta )|W|$
such that the pair
$|M| = (1-\delta )|W|$
such that the pair
![]() $(M,V)$
is
$(M,V)$
is
![]() $(\varepsilon ',d^3/32)$
-super-regular with respect to the auxiliary graph
$(\varepsilon ',d^3/32)$
-super-regular with respect to the auxiliary graph
![]() $H_G(M,V)$
.
$H_G(M,V)$
.
We will prove this lemma at the end of this section. For Lemma 4.2, we will use the minimum degree condition and
![]() $G(V,p)$
to find additional triangles covering the remaining vertices from
$G(V,p)$
to find additional triangles covering the remaining vertices from
![]() $U$
and
$U$
and
![]() $W$
that are not covered by
$W$
that are not covered by
![]() $M$
. We now proceed to the details of this proof.
$M$
. We now proceed to the details of this proof.
Proof of Lemma 4.2.Given
![]() $0 \lt \delta ' \le d \lt 1$
, let
$0 \lt \delta ' \le d \lt 1$
, let
![]() $\varepsilon '\gt 0$
be given by Lemma 3.4 on input
$\varepsilon '\gt 0$
be given by Lemma 3.4 on input
![]() $d^3/64$
and let
$d^3/64$
and let
![]() $0\lt \delta \lt \delta _0 \le \min \{ \delta ', d^3/22 \}$
. Furthermore, let
$0\lt \delta \lt \delta _0 \le \min \{ \delta ', d^3/22 \}$
. Furthermore, let
![]() $C \ge 8 \delta ^{-2}$
, let
$C \ge 8 \delta ^{-2}$
, let
![]() $0\lt \varepsilon \lt \delta/4$
be given by Lemma 8.1 on input
$0\lt \varepsilon \lt \delta/4$
be given by Lemma 8.1 on input
![]() $d$
,
$d$
,
![]() $\tfrac{\delta }{3(1-\delta )}$
(in place of
$\tfrac{\delta }{3(1-\delta )}$
(in place of
![]() $\delta$
), and
$\delta$
), and
![]() $\varepsilon '/2$
and let
$\varepsilon '/2$
and let
![]() $p \ge C/n$
.
$p \ge C/n$
.
Suppose
![]() $U$
,
$U$
,
![]() $V$
,
$V$
,
![]() $W$
are disjoint sets of size
$W$
are disjoint sets of size
![]() $|V|=n$
and
$|V|=n$
and
![]() $(1-\delta _0)n \le |U|=|W| \le (1-\delta )n$
with
$(1-\delta _0)n \le |U|=|W| \le (1-\delta )n$
with
![]() $|V|+|U|+|W| \equiv 0 \pmod 3$
, and
$|V|+|U|+|W| \equiv 0 \pmod 3$
, and
![]() $G$
is a graph with vertex set
$G$
is a graph with vertex set
![]() $U \cup V \cup W$
such that the pairs
$U \cup V \cup W$
such that the pairs
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
are
$(V,W)$
are
![]() $(\varepsilon,d)$
-super-regular with respect to
$(\varepsilon,d)$
-super-regular with respect to
![]() $G$
. Let
$G$
. Let
![]() $\delta _1$
be such that
$\delta _1$
be such that
![]() $|U|=|W|=(1-\delta _1)n$
and observe that
$|U|=|W|=(1-\delta _1)n$
and observe that
![]() $\delta \le \delta _1 \le \delta _0$
. We reveal random edges
$\delta \le \delta _1 \le \delta _0$
. We reveal random edges
![]() $G_1 \sim G(U,W,p)$
and
$G_1 \sim G(U,W,p)$
and
![]() $G_2 \sim G(V,p)$
and we have that a.a.s. any set of size at least
$G_2 \sim G(V,p)$
and we have that a.a.s. any set of size at least
![]() $\delta n$
in
$\delta n$
in
![]() $V$
contains an edge of
$V$
contains an edge of
![]() $G_2$
. Indeed, fixed a set of size at least
$G_2$
. Indeed, fixed a set of size at least
![]() $\delta n$
, the probability that it does not contain an edge of
$\delta n$
, the probability that it does not contain an edge of
![]() $G_2$
is at most
$G_2$
is at most
![]() $(1-p)^{\binom{\delta n}{2}} \le \exp (-p\binom{\delta n}{2}) \le \exp (-2n)$
since
$(1-p)^{\binom{\delta n}{2}} \le \exp (-p\binom{\delta n}{2}) \le \exp (-2n)$
since
![]() $C \ge 8 \delta ^{-2}$
, and we conclude by a union bound over the at most
$C \ge 8 \delta ^{-2}$
, and we conclude by a union bound over the at most
![]() $2^n$
choices of such set. Then we apply Lemma 8.1 with
$2^n$
choices of such set. Then we apply Lemma 8.1 with
![]() $G_1$
to obtain a matching
$G_1$
to obtain a matching
![]() $M \subseteq G_1$
of size
$M \subseteq G_1$
of size
![]() $|M| = \left (1-\tfrac{\delta }{3(1-\delta )}\right )|W|=\left (1-\tfrac{\delta }{3(1-\delta )}\right )(1-\delta _1)n$
such that the pair
$|M| = \left (1-\tfrac{\delta }{3(1-\delta )}\right )|W|=\left (1-\tfrac{\delta }{3(1-\delta )}\right )(1-\delta _1)n$
such that the pair
![]() $(M,V)$
is
$(M,V)$
is
![]() $(\varepsilon '/2,d^3/32)$
-super-regular with respect to
$(\varepsilon '/2,d^3/32)$
-super-regular with respect to
![]() $H_G(M,V)$
. As for
$H_G(M,V)$
. As for
![]() $x \in (0,1)$
the function
$x \in (0,1)$
the function
![]() $x \rightarrow x/(1-x)$
is increasing and
$x \rightarrow x/(1-x)$
is increasing and
![]() $\delta \le \delta _1$
, we have
$\delta \le \delta _1$
, we have
![]() $\left (\tfrac{\delta _1}{3}-\tfrac{\delta }{3(1-\delta )}(1-\delta _1) \right ) \ge \left (\tfrac{\delta _1}{3}-\tfrac{\delta _1}{3(1-\delta _1)}(1-\delta _1) \right ) \ge 0$
. Thus, by ignoring
$\left (\tfrac{\delta _1}{3}-\tfrac{\delta }{3(1-\delta )}(1-\delta _1) \right ) \ge \left (\tfrac{\delta _1}{3}-\tfrac{\delta _1}{3(1-\delta _1)}(1-\delta _1) \right ) \ge 0$
. Thus, by ignoring
![]() $\left (\tfrac{\delta _1}{3}-\tfrac{\delta }{3(1-\delta )}(1-\delta _1) \right ) n \le d^3 n/64$
edges of
$\left (\tfrac{\delta _1}{3}-\tfrac{\delta }{3(1-\delta )}(1-\delta _1) \right ) n \le d^3 n/64$
edges of
![]() $M$
, we get a subset
$M$
, we get a subset
![]() $M' \subseteq M$
with
$M' \subseteq M$
with
![]() $|M'|=(1-4 \delta _1/3) n$
.
$|M'|=(1-4 \delta _1/3) n$
.
Next, let
![]() $U' = U \setminus V(M')$
and
$U' = U \setminus V(M')$
and
![]() $W'=W \setminus V(M')$
be the sets of vertices in
$W'=W \setminus V(M')$
be the sets of vertices in
![]() $U$
and
$U$
and
![]() $W$
, respectively, that are not incident to edges of
$W$
, respectively, that are not incident to edges of
![]() $M'$
. Note that both
$M'$
. Note that both
![]() $U'$
and
$U'$
and
![]() $W'$
have size
$W'$
have size
![]() $\delta _1 n/3$
. We want to cover these vertices with triangles having the other two vertices in
$\delta _1 n/3$
. We want to cover these vertices with triangles having the other two vertices in
![]() $V$
. Any vertex
$V$
. Any vertex
![]() $v \in U' \cup W'$
has degree at least
$v \in U' \cup W'$
has degree at least
![]() $d n$
into
$d n$
into
![]() $V$
and as
$V$
and as
![]() $d \gt 2 \delta _0 \ge 2 \delta _1$
, we can pick these triangles greedily for each
$d \gt 2 \delta _0 \ge 2 \delta _1$
, we can pick these triangles greedily for each
![]() $v \in U' \cup W'$
using
$v \in U' \cup W'$
using
![]() $G_2$
. Let
$G_2$
. Let
![]() $V' \subseteq V$
be the vertices that were used for these triangles and observe
$V' \subseteq V$
be the vertices that were used for these triangles and observe
![]() $|V \setminus V'|=|M'|=(1-4 \delta _1/3)n$
.
$|V \setminus V'|=|M'|=(1-4 \delta _1/3)n$
.
To obtain the triangle factor it remains to find a perfect matching in
![]() $H_G(M',V \setminus V')$
. By Lemma 3.4, it is sufficient to observe that the pair
$H_G(M',V \setminus V')$
. By Lemma 3.4, it is sufficient to observe that the pair
![]() $(M',V \setminus V')$
is
$(M',V \setminus V')$
is
![]() $(\varepsilon ',d^3/64)$
-super-regular with respect to
$(\varepsilon ',d^3/64)$
-super-regular with respect to
![]() $H_G(M',V \setminus V')$
, which holds because
$H_G(M',V \setminus V')$
, which holds because
![]() $(M,V)$
is
$(M,V)$
is
![]() $(\varepsilon '/2,d^3/32)$
-super-regular with respect to
$(\varepsilon '/2,d^3/32)$
-super-regular with respect to
![]() $H_G(M,V)$
.
$H_G(M,V)$
.
Now we turn to the overview of the proof of Lemma 4.1, for which
![]() $p \ge C \log n/n$
. We will rely again on Lemma 8.1, which gives a large matching
$p \ge C \log n/n$
. We will rely again on Lemma 8.1, which gives a large matching
![]() $M \subseteq G(U,W,p)$
such that the pair
$M \subseteq G(U,W,p)$
such that the pair
![]() $(M,V)$
is super-regular with respect to the auxiliary graph
$(M,V)$
is super-regular with respect to the auxiliary graph
![]() $H_G(M,V)$
. Starting from this matching
$H_G(M,V)$
. Starting from this matching
![]() $M$
, we add more matching edges of
$M$
, we add more matching edges of
![]() $G(U,W,p)$
between the vertices not covered by
$G(U,W,p)$
between the vertices not covered by
![]() $M$
, and extend
$M$
, and extend
![]() $M$
to a perfect matching in
$M$
to a perfect matching in
![]() $G(U,W,p)$
. This will be possible using Lemma 8.2 from below and Lemma 3.6, where we emphasise that the
$G(U,W,p)$
. This will be possible using Lemma 8.2 from below and Lemma 3.6, where we emphasise that the
![]() $\log n$
-term is essential for this last lemma. It is then easy to find a perfect matching in
$\log n$
-term is essential for this last lemma. It is then easy to find a perfect matching in
![]() $H_G(M,V)$
that gives a triangle factor.
$H_G(M,V)$
that gives a triangle factor.
Before we come to the proof of Lemma 4.1, we introduce another auxiliary structure to describe in general which potential edges between
![]() $U$
and
$U$
and
![]() $W$
we would like to use for the matching
$W$
we would like to use for the matching
![]() $M$
. We define an auxiliary bipartite graph
$M$
. We define an auxiliary bipartite graph
![]() $F=F_{G,V}(U,W)$
with bipartition
$F=F_{G,V}(U,W)$
with bipartition
![]() $U \cup W$
, where a pair
$U \cup W$
, where a pair
![]() $(u,w) \in U \times W$
is an edge of
$(u,w) \in U \times W$
is an edge of
![]() $F$
if
$F$
if
![]() $u$
and
$u$
and
![]() $w$
have at least
$w$
have at least
![]() $d^2 n/2$
common neighbours in
$d^2 n/2$
common neighbours in
![]() $G$
, i.e.
$G$
, i.e.
![]() $|N_G(u,V) \cap N_G(w,V)| \ge d^2 n/2$
. Similarly, for a set
$|N_G(u,V) \cap N_G(w,V)| \ge d^2 n/2$
. Similarly, for a set
![]() $X \subseteq V$
, we call an edge
$X \subseteq V$
, we call an edge
![]() $uw \in E(F)$
good for
$uw \in E(F)$
good for
![]() $X$
if there are at least
$X$
if there are at least
![]() $d^2|X|/2$
vertices
$d^2|X|/2$
vertices
![]() $x \in X$
that are incident to
$x \in X$
that are incident to
![]() $u$
and
$u$
and
![]() $w$
in
$w$
in
![]() $G$
, i.e.
$G$
, i.e.
![]() $uwx$
is a triangle in
$uwx$
is a triangle in
![]() $G \cup F$
. We denote the spanning subgraph of
$G \cup F$
. We denote the spanning subgraph of
![]() $F$
with edges that are good for
$F$
with edges that are good for
![]() $X$
by
$X$
by
![]() $F_X$
. We prove the following lemma, which will be used in the proof of Lemma 8.1 to construct
$F_X$
. We prove the following lemma, which will be used in the proof of Lemma 8.1 to construct
![]() $M$
and in the proof of Lemma 4.1 to extend
$M$
and in the proof of Lemma 4.1 to extend
![]() $M$
.
$M$
.
Lemma 8.2.
For any
![]() $\varepsilon,d\gt 0$
with
$\varepsilon,d\gt 0$
with
![]() $\varepsilon \le d/2$
, the following holds. Let
$\varepsilon \le d/2$
, the following holds. Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $U \cup V \cup W$
, with
$U \cup V \cup W$
, with
![]() $|V|=n$
and
$|V|=n$
and
![]() $(1-1/2)n \le |U|=n_0=|W| \le (1 + 1/2) n$
, such that
$(1-1/2)n \le |U|=n_0=|W| \le (1 + 1/2) n$
, such that
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
are
$(V,W)$
are
![]() $(\varepsilon,d)$
-super-regular pairs with respect to
$(\varepsilon,d)$
-super-regular pairs with respect to
![]() $G$
. Let
$G$
. Let
![]() $F=F_{G,V}(U,W)$
be the bipartite graph described above. Then
$F=F_{G,V}(U,W)$
be the bipartite graph described above. Then
![]() $F$
satisfies the following properties.
$F$
satisfies the following properties.
-
(i) The minimum degree of
 $F$
is at least
$F$
is at least
 $(1-\varepsilon )n_0$
.
$(1-\varepsilon )n_0$
. -
(ii) If
 $X \subseteq V$
and
$X \subseteq V$
and
 $|X| \ge 2\varepsilon n/d$
, then all but at most
$|X| \ge 2\varepsilon n/d$
, then all but at most
 $\varepsilon n_0$
vertices from
$\varepsilon n_0$
vertices from
 $U$
have degree at least
$U$
have degree at least
 $(1-2\varepsilon )n_0$
in
$(1-2\varepsilon )n_0$
in
 $F_X$
.
$F_X$
.
Proof of Lemma 8.2.Take any
![]() $u \in U$
. Since
$u \in U$
. Since
![]() $(U,V)$
is an
$(U,V)$
is an
![]() $(\varepsilon,d)$
-super-regular pair, we have
$(\varepsilon,d)$
-super-regular pair, we have
![]() $|N_G(u,V)| \ge d |V| \ge \varepsilon |V|$
and we can apply Lemma 3.3 with
$|N_G(u,V)| \ge d |V| \ge \varepsilon |V|$
and we can apply Lemma 3.3 with
![]() $A=W$
,
$A=W$
,
![]() $B=V$
, and
$B=V$
, and
![]() $Y=N_G(u,V)$
to conclude that the set
$Y=N_G(u,V)$
to conclude that the set
has size at least
![]() $(1-\varepsilon )n_0$
. Since
$(1-\varepsilon )n_0$
. Since
![]() $(d-\varepsilon ) |Y| \geq (d-\varepsilon ) d n \ge d^2n/2$
, all the vertices in
$(d-\varepsilon ) |Y| \geq (d-\varepsilon ) d n \ge d^2n/2$
, all the vertices in
![]() $W_u$
are neighbours of
$W_u$
are neighbours of
![]() $u$
in the auxiliary graph
$u$
in the auxiliary graph
![]() $F$
and, therefore,
$F$
and, therefore,
![]() $|N_F(u)| \ge (1-\varepsilon ) n_0$
. Analogously, we infer that
$|N_F(u)| \ge (1-\varepsilon ) n_0$
. Analogously, we infer that
![]() $|N_F(w)| \ge (1-\varepsilon ) n_0$
for all
$|N_F(w)| \ge (1-\varepsilon ) n_0$
for all
![]() $w \in W$
and hence
$w \in W$
and hence
![]() $\delta (F) \ge (1-\varepsilon )n_0$
.
$\delta (F) \ge (1-\varepsilon )n_0$
.
If
![]() $|X| \ge 2 \varepsilon n/d$
, then by Lemma 3.3 all but at most
$|X| \ge 2 \varepsilon n/d$
, then by Lemma 3.3 all but at most
![]() $\varepsilon n_0$
vertices
$\varepsilon n_0$
vertices
![]() $u \in U$
have at least
$u \in U$
have at least
![]() $d|X|/2$
neighbours in
$d|X|/2$
neighbours in
![]() $X$
. Fixing any
$X$
. Fixing any
![]() $u \in U$
with this property, and again using Lemma 3.3, all but at most
$u \in U$
with this property, and again using Lemma 3.3, all but at most
![]() $\varepsilon n_0$
vertices
$\varepsilon n_0$
vertices
![]() $w \in W$
have at least
$w \in W$
have at least
![]() $d^2|X|/4$
common neighbours with
$d^2|X|/4$
common neighbours with
![]() $u$
in
$u$
in
![]() $X$
. From (i) we know that
$X$
. From (i) we know that
![]() $\delta (F) \ge (1-\varepsilon )n_0$
, therefore all but at most
$\delta (F) \ge (1-\varepsilon )n_0$
, therefore all but at most
![]() $\varepsilon n_0$
vertices from
$\varepsilon n_0$
vertices from
![]() $U$
have degree at least
$U$
have degree at least
![]() $(1-2\varepsilon )n_0$
in
$(1-2\varepsilon )n_0$
in
![]() $F_X$
.
$F_X$
.
Now we prove Lemma 4.1 using Lemmas 8.1 and 8.2.
Proof of Lemma 4.1.Given
![]() $d\in (0,1)$
, let
$d\in (0,1)$
, let
![]() $\varepsilon '\gt 0$
be given by Lemma 3.4 on input
$\varepsilon '\gt 0$
be given by Lemma 3.4 on input
![]() $d^3/64$
and let
$d^3/64$
and let
![]() $0\lt \delta \lt d^3/64$
. Furthermore, let
$0\lt \delta \lt d^3/64$
. Furthermore, let
![]() $0\lt \varepsilon \lt \delta/4$
be given by Lemma 8.1 on input
$0\lt \varepsilon \lt \delta/4$
be given by Lemma 8.1 on input
![]() $d$
,
$d$
,
![]() $\delta$
, and
$\delta$
, and
![]() $\varepsilon '/2$
, let
$\varepsilon '/2$
, let
![]() $C'$
be given by Lemma 3.6 for input
$C'$
be given by Lemma 3.6 for input
![]() $1/4$
, set
$1/4$
, set
![]() $C = 2 C'/\delta$
, and let
$C = 2 C'/\delta$
, and let
![]() $p \ge C \log n/n$
.
$p \ge C \log n/n$
.
Now let
![]() $G$
be a graph on
$G$
be a graph on
![]() $U \cup V \cup W$
, with
$U \cup V \cup W$
, with
![]() $|U|=|V|=|W|=n$
, such that
$|U|=|V|=|W|=n$
, such that
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
are
$(V,W)$
are
![]() $(\varepsilon,d)$
-super-regular pairs with respect to
$(\varepsilon,d)$
-super-regular pairs with respect to
![]() $G$
. We reveal the random edges in
$G$
. We reveal the random edges in
![]() $G(U,W,p)$
in two rounds as
$G(U,W,p)$
in two rounds as
![]() $G_1 \sim G(U,W,p/2)$
and
$G_1 \sim G(U,W,p/2)$
and
![]() $G_2 \sim G(U,W,p/2)$
. We apply Lemma 8.1 with
$G_2 \sim G(U,W,p/2)$
. We apply Lemma 8.1 with
![]() $G_1$
to a.a.s. obtain a matching
$G_1$
to a.a.s. obtain a matching
![]() $M \subseteq G_1$
of size
$M \subseteq G_1$
of size
![]() $|M| = (1-\delta )n$
such that the pair
$|M| = (1-\delta )n$
such that the pair
![]() $(M,V)$
is
$(M,V)$
is
![]() $(\varepsilon '/2,d^3/32)$
-super-regular with respect to
$(\varepsilon '/2,d^3/32)$
-super-regular with respect to
![]() $H_G(M,V)$
. Observe that
$H_G(M,V)$
. Observe that
![]() $p \ge C \log n/n$
, while the logarithmic factor is not required by Lemma 8.1, and thus the constant
$p \ge C \log n/n$
, while the logarithmic factor is not required by Lemma 8.1, and thus the constant
![]() $C$
does not need to depend on the constant given by this lemma.
$C$
does not need to depend on the constant given by this lemma.
Next, let
![]() $U' = U \setminus V(M)$
and
$U' = U \setminus V(M)$
and
![]() $W'=W \setminus V(M)$
be the sets of vertices in
$W'=W \setminus V(M)$
be the sets of vertices in
![]() $U$
and
$U$
and
![]() $W$
respectively that are not incident to edges of
$W$
respectively that are not incident to edges of
![]() $M$
. Note that both
$M$
. Note that both
![]() $U'$
and
$U'$
and
![]() $W'$
have size
$W'$
have size
![]() $\delta n$
. For the auxiliary graph
$\delta n$
. For the auxiliary graph
![]() $F=F_{G,V}(U,W)$
defined above, we consider the subgraph
$F=F_{G,V}(U,W)$
defined above, we consider the subgraph
![]() $F[U',W']$
induced by
$F[U',W']$
induced by
![]() $U'$
and
$U'$
and
![]() $W'$
and note that by Lemma 8.2 (i) it has minimum degree at least
$W'$
and note that by Lemma 8.2 (i) it has minimum degree at least
![]() $(\delta -\varepsilon ) n \ge \frac{3}{4} \delta n$
. We use
$(\delta -\varepsilon ) n \ge \frac{3}{4} \delta n$
. We use
![]() $G_2$
to reveal the edges of
$G_2$
to reveal the edges of
![]() $F[U',W']$
with probability
$F[U',W']$
with probability
![]() $p/2$
and a.a.s. by Lemma 3.6 with
$p/2$
and a.a.s. by Lemma 3.6 with
![]() $p/2 \ge C' \log (\delta n)/(\delta n)$
we find a perfect matching
$p/2 \ge C' \log (\delta n)/(\delta n)$
we find a perfect matching
![]() $M'$
in
$M'$
in
![]() $G_2 \cap F[U',W']$
.
$G_2 \cap F[U',W']$
.
To obtain the triangle factor, it remains to find a perfect matching in
![]() $H_G(M \cup M',V)$
. For this we first greedily select a neighbour
$H_G(M \cup M',V)$
. For this we first greedily select a neighbour
![]() $v$
from
$v$
from
![]() $V$
for each
$V$
for each
![]() $m \in M'$
and denote the set of vertices
$m \in M'$
and denote the set of vertices
![]() $v$
used in this way by
$v$
used in this way by
![]() $V'$
. Since
$V'$
. Since
![]() $|V'|=|M'|=\delta n$
, it follows from the choice of
$|V'|=|M'|=\delta n$
, it follows from the choice of
![]() $\delta$
that this is possible and that the pair
$\delta$
that this is possible and that the pair
![]() $(M,V \setminus V')$
is
$(M,V \setminus V')$
is
![]() $(\varepsilon ',d^3/64)$
-super-regular with respect to
$(\varepsilon ',d^3/64)$
-super-regular with respect to
![]() $H_G(M,V \setminus V')$
. As
$H_G(M,V \setminus V')$
. As
![]() $|V \setminus V'|=|M|$
, by Lemma 3.4, there is a perfect matching in
$|V \setminus V'|=|M|$
, by Lemma 3.4, there is a perfect matching in
![]() $H_G(M,V \setminus V')$
and we are done.
$H_G(M,V \setminus V')$
and we are done.
It remains to prove Lemma 8.1.
Proof of Lemma 8.1.Given
![]() $0 \lt d,\delta,\varepsilon ' \lt 1$
with
$0 \lt d,\delta,\varepsilon ' \lt 1$
with
![]() $2\delta \le d$
, suppose that
$2\delta \le d$
, suppose that
are positive real numbers such that
Furthermore, let
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $p \ge C/n$
is large enough for the applications of Chernoff’s inequality below.
$p \ge C/n$
is large enough for the applications of Chernoff’s inequality below.
Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $U \cup V \cup W$
, with
$U \cup V \cup W$
, with
![]() $|V|=n$
and
$|V|=n$
and
![]() $|U|=|W|=n_0=(1 \pm 1/2)n$
, such that
$|U|=|W|=n_0=(1 \pm 1/2)n$
, such that
![]() $(V,U)$
and
$(V,U)$
and
![]() $(V,W)$
are
$(V,W)$
are
![]() $(\varepsilon,d)$
-super-regular pairs with respect to
$(\varepsilon,d)$
-super-regular pairs with respect to
![]() $G$
. To find the matching
$G$
. To find the matching
![]() $M$
, construct a graph
$M$
, construct a graph
![]() $\tilde{F} \subseteq F=F_{G,V}(U,W)$
by including each edge of
$\tilde{F} \subseteq F=F_{G,V}(U,W)$
by including each edge of
![]() $F$
randomly with probability
$F$
randomly with probability
![]() $p$
, independently from all other edges.
$p$
, independently from all other edges.
Claim 8.3.
A.a.s. for every
![]() $X \subseteq V$
of size
$X \subseteq V$
of size
![]() $\eta n$
and
$\eta n$
and
![]() $U'\subseteq U$
and
$U'\subseteq U$
and
![]() $W' \subseteq W$
both of size at least
$W' \subseteq W$
both of size at least
![]() $\delta n_0$
, the following statements hold.
$\delta n_0$
, the following statements hold.
and
Proof. The expected number of edges between
![]() $U'$
and
$U'$
and
![]() $W'$
in
$W'$
in
![]() $\tilde{F}$
is by Lemma 8.2 (i) at least
$\tilde{F}$
is by Lemma 8.2 (i) at least
![]() $e_F(U',W') p \ge |U'|(|W'|-\varepsilon n_0) p \ge C\delta ^2 n/8$
. Using Chernoff’s inequality (Lemma 3.1), we obtain with
$e_F(U',W') p \ge |U'|(|W'|-\varepsilon n_0) p \ge C\delta ^2 n/8$
. Using Chernoff’s inequality (Lemma 3.1), we obtain with
![]() $C \delta ^2 \varepsilon ^2 \ge 120$
that
$C \delta ^2 \varepsilon ^2 \ge 120$
that
From Lemma 8.2 (ii) we get that the expected number of edges between
![]() $U'$
and
$U'$
and
![]() $W'$
in
$W'$
in
![]() $\tilde{F}$
that are good for
$\tilde{F}$
that are good for
![]() $X$
is at least
$X$
is at least
![]() $(|U'|-\varepsilon n_0)(|W'|-2\varepsilon n_0) p \ge (1-3 \varepsilon/\delta ) |U'| |W'| p$
. Moreover, observe that
$(|U'|-\varepsilon n_0)(|W'|-2\varepsilon n_0) p \ge (1-3 \varepsilon/\delta ) |U'| |W'| p$
. Moreover, observe that
Thus, by Chernoff’s inequality applied with
![]() $\tfrac{4\varepsilon/\delta }{\sqrt{1-3\varepsilon/\delta }}$
in place of
$\tfrac{4\varepsilon/\delta }{\sqrt{1-3\varepsilon/\delta }}$
in place of
![]() $\delta$
, we get with
$\delta$
, we get with
![]() $C \varepsilon ^2 \ge 3$
that
$C \varepsilon ^2 \ge 3$
that
Claim 8.3 follows from the union bound over the at most
![]() $2^{3n}$
choices for
$2^{3n}$
choices for
![]() $X$
,
$X$
,
![]() $U'$
, and
$U'$
, and
![]() $W'$
.
$W'$
.
Using a random greedy process, we now choose a matching
![]() $M$
of size
$M$
of size
![]() $(1-\delta )|W|$
between
$(1-\delta )|W|$
between
![]() $U$
and
$U$
and
![]() $W$
in
$W$
in
![]() $\tilde{F}$
as follows. Having chosen edges
$\tilde{F}$
as follows. Having chosen edges
![]() $m_1,\dots,m_t\in \tilde{F}$
with
$m_1,\dots,m_t\in \tilde{F}$
with
![]() $t\lt (1-\delta )|W|$
, we pick
$t\lt (1-\delta )|W|$
, we pick
![]() $m_{t+1}$
uniformly at random from all edges of
$m_{t+1}$
uniformly at random from all edges of
![]() $\tilde{F}$
that do not share an endpoint with any of
$\tilde{F}$
that do not share an endpoint with any of
![]() $m_1,\dots,m_t$
. This is possible since, by (8) and Lemma 8.2 (i), between any two subsets of
$m_1,\dots,m_t$
. This is possible since, by (8) and Lemma 8.2 (i), between any two subsets of
![]() $U$
and
$U$
and
![]() $W$
of size
$W$
of size
![]() $\delta |W|$
there is at least one edge of
$\delta |W|$
there is at least one edge of
![]() $\tilde{F}$
. For
$\tilde{F}$
. For
![]() $i=1,\dots,(1-\delta ) n$
we denote by
$i=1,\dots,(1-\delta ) n$
we denote by
![]() $\mathcal{H}_i$
the history
$\mathcal{H}_i$
the history
![]() $m_1,\dots,m_i$
. It remains to show that
$m_1,\dots,m_i$
. It remains to show that
![]() $(M,V)$
is
$(M,V)$
is
![]() $(\varepsilon ',d^3/32)$
-super-regular with respect to the auxiliary graph
$(\varepsilon ',d^3/32)$
-super-regular with respect to the auxiliary graph
![]() $H=H_G(M,V)$
.
$H=H_G(M,V)$
.
Observe, that any
![]() $m \in M$
has
$m \in M$
has
![]() $|N_H(m)| \ge d^2n/2$
by construction. We now show that for any
$|N_H(m)| \ge d^2n/2$
by construction. We now show that for any
![]() $v \in V$
we have
$v \in V$
we have
![]() $|N_H(v)| \ge d^3 n_0/32$
. For this, it is sufficient to consider the first
$|N_H(v)| \ge d^3 n_0/32$
. For this, it is sufficient to consider the first
![]() $dn_0/2$
edges
$dn_0/2$
edges
![]() $m_1, \dots, m_{dn_0/2}$
that are chosen for
$m_1, \dots, m_{dn_0/2}$
that are chosen for
![]() $M$
by the random greedy process. For
$M$
by the random greedy process. For
![]() $i=1,\dots,dn_0/2$
, by (8), there are at most
$i=1,\dots,dn_0/2$
, by (8), there are at most
![]() $e(\tilde{F}) \le (1+\varepsilon )n_0^2p$
available edges to chose
$e(\tilde{F}) \le (1+\varepsilon )n_0^2p$
available edges to chose
![]() $m_i$
from. On the other hand, as long as
$m_i$
from. On the other hand, as long as
![]() $i \le dn_0/2$
, the vertex
$i \le dn_0/2$
, the vertex
![]() $v$
has at least
$v$
has at least
![]() $d n_0/2$
neighbours in each of the sets
$d n_0/2$
neighbours in each of the sets
![]() $U$
and
$U$
and
![]() $W$
in
$W$
in
![]() $G$
that are not covered by the edges in
$G$
that are not covered by the edges in
![]() $\mathcal{H}_{i-1}$
. Let
$\mathcal{H}_{i-1}$
. Let
![]() $U' \subseteq U$
and
$U' \subseteq U$
and
![]() $W' \subseteq W$
be the sets of those vertices and observe that
$W' \subseteq W$
be the sets of those vertices and observe that
![]() $|U'|,|W'| \ge d n_0/2 \ge \delta n_0$
. Therefore, by (8) and Lemma 8.2 (i), there are at least
$|U'|,|W'| \ge d n_0/2 \ge \delta n_0$
. Therefore, by (8) and Lemma 8.2 (i), there are at least
edges in
![]() $\tilde{F}[(U \cup W) \setminus V(\mathcal{H}_{i-1})]$
available to choose
$\tilde{F}[(U \cup W) \setminus V(\mathcal{H}_{i-1})]$
available to choose
![]() $m_i$
from, such that both endpoints of
$m_i$
from, such that both endpoints of
![]() $m_i$
are incident to
$m_i$
are incident to
![]() $v$
in
$v$
in
![]() $G$
.
$G$
.
Hence, for
![]() $i=1,\dots,dn_0/2$
, we get
$i=1,\dots,dn_0/2$
, we get
As this holds independently of the history of the process, this process dominates a binomial distribution with parameters
![]() $dn_0/2$
and
$dn_0/2$
and
![]() $d^2/8$
. Therefore, even though the events are not mutually independent, we can use Chernoff’s inequality to infer that
$d^2/8$
. Therefore, even though the events are not mutually independent, we can use Chernoff’s inequality to infer that
![]() $|N_H(v)| \ge d^3n_0/32$
with probability at least
$|N_H(v)| \ge d^3n_0/32$
with probability at least
![]() $1-1/n^2$
. Then, by applying the union bound over all
$1-1/n^2$
. Then, by applying the union bound over all
![]() $v \in V$
, we obtain that indeed a.a.s.
$v \in V$
, we obtain that indeed a.a.s.
![]() $|N_H(v)| \ge d^3 n_0/32$
for all
$|N_H(v)| \ge d^3 n_0/32$
for all
![]() $v \in V$
.
$v \in V$
.
Now we show the regularity of
![]() $H=H_G(M,V)$
. Let
$H=H_G(M,V)$
. Let
![]() $X \subseteq V$
be given with
$X \subseteq V$
be given with
![]() $|X| = \eta n$
. For
$|X| = \eta n$
. For
![]() $i=0$
,
$i=0$
,
![]() $1,\dots,t-1$
, we obtain from (8) that there are at most
$1,\dots,t-1$
, we obtain from (8) that there are at most
![]() $(1+\varepsilon ) (n_0-i)^2 p$
edges in
$(1+\varepsilon ) (n_0-i)^2 p$
edges in
![]() $\tilde{F}[(U \cup W) \setminus V(\mathcal{H}_i)]$
available for choosing
$\tilde{F}[(U \cup W) \setminus V(\mathcal{H}_i)]$
available for choosing
![]() $m_{i+1}$
, of which, by (9), at least
$m_{i+1}$
, of which, by (9), at least
![]() $(1-7\varepsilon/\delta ) (n_0 - i)^2 p$
are good for
$(1-7\varepsilon/\delta ) (n_0 - i)^2 p$
are good for
![]() $X$
. Then
$X$
. Then
As the upper bound on the probability holds independently of the history, this process is dominated by a binomial distribution with parameters
![]() $(1-\delta )n_0$
and
$(1-\delta )n_0$
and
![]() $8 \varepsilon/\delta$
. Observe that the expected value of this distribution is
$8 \varepsilon/\delta$
. Observe that the expected value of this distribution is
![]() $(1-\delta ) n_0 \, 8\varepsilon/\delta \le 8 \varepsilon n_0/\delta$
. Then, with
$(1-\delta ) n_0 \, 8\varepsilon/\delta \le 8 \varepsilon n_0/\delta$
. Then, with
![]() $B_X \subseteq M$
being the edges in
$B_X \subseteq M$
being the edges in
![]() $M$
that are not good for
$M$
that are not good for
![]() $X$
and as
$X$
and as
![]() $\gamma n_0 \ge 7 \cdot 8 \varepsilon n_0/\delta$
, we get from Chernoff’s inequality (second part of Lemma 3.1) that
$\gamma n_0 \ge 7 \cdot 8 \varepsilon n_0/\delta$
, we get from Chernoff’s inequality (second part of Lemma 3.1) that
There are at most
![]() $\binom{n}{\eta n} \le \left (e/\eta \right )^{\eta n} \le \exp (\eta \log (1/\eta ) n) \le \exp (\gamma n_0/2)$
choices for
$\binom{n}{\eta n} \le \left (e/\eta \right )^{\eta n} \le \exp (\eta \log (1/\eta ) n) \le \exp (\gamma n_0/2)$
choices for
![]() $X$
and, thus, with the union bound over all these choices, we obtain that a.a.s. there are at most
$X$
and, thus, with the union bound over all these choices, we obtain that a.a.s. there are at most
![]() $\gamma n_0$
bad edges in
$\gamma n_0$
bad edges in
![]() $M$
for any
$M$
for any
![]() $X \subseteq V$
with
$X \subseteq V$
with
![]() $|X|=\eta n$
.
$|X|=\eta n$
.
Therefore for any set
![]() $X' \subseteq V$
and
$X' \subseteq V$
and
![]() $M'\subseteq M$
with
$M'\subseteq M$
with
![]() $|X'| \ge \varepsilon ' n$
and
$|X'| \ge \varepsilon ' n$
and
![]() $|M'|\ge \varepsilon ' |M|$
we find
$|M'|\ge \varepsilon ' |M|$
we find
Overall, we can conclude the pair
![]() $(M,V)$
is
$(M,V)$
is
![]() $(\varepsilon ',d^3/32)$
-super-regular with respect to the auxiliary graph
$(\varepsilon ',d^3/32)$
-super-regular with respect to the auxiliary graph
![]() $H_G(M,V)$
.
$H_G(M,V)$
.
8.2 Proof of Lemma 4.3
Lemma 4.3 easily follows from Lemma 4.2 after splitting the sets
![]() $U$
and
$U$
and
![]() $V$
appropriately.
$V$
appropriately.
Proof of Lemma 4.3.Let
![]() $0\lt d\lt 1$
, choose
$0\lt d\lt 1$
, choose
![]() $\delta '$
with
$\delta '$
with
![]() $0 \lt \delta ' \le d/4$
and apply Lemma 4.2 with
$0 \lt \delta ' \le d/4$
and apply Lemma 4.2 with
![]() $\delta '$
and
$\delta '$
and
![]() $d/4$
to obtain
$d/4$
to obtain
![]() $\delta _0,\delta,\varepsilon '$
with
$\delta _0,\delta,\varepsilon '$
with
![]() $\delta ' \ge \delta _0 \gt \delta \gt \varepsilon '\gt 0$
and
$\delta ' \ge \delta _0 \gt \delta \gt \varepsilon '\gt 0$
and
![]() $C'\gt 0$
. Then let
$C'\gt 0$
. Then let
![]() $\varepsilon$
with
$\varepsilon$
with
![]() $0 \lt \varepsilon \le \varepsilon '/8$
and
$0 \lt \varepsilon \le \varepsilon '/8$
and
![]() $C \ge 10 C'$
. Next let
$C \ge 10 C'$
. Next let
![]() $U$
and
$U$
and
![]() $V$
be vertex sets of size
$V$
be vertex sets of size
![]() $|V|=n$
and
$|V|=n$
and
![]() $3n/4 \le |U|=n_0 \le n$
where
$3n/4 \le |U|=n_0 \le n$
where
![]() $n+n_0 \equiv 0 \pmod 3$
and assume that
$n+n_0 \equiv 0 \pmod 3$
and assume that
![]() $(U,V)$
is a
$(U,V)$
is a
![]() $(\varepsilon,d)$
-super-regular pair.
$(\varepsilon,d)$
-super-regular pair.
The idea is to split the regular pair
![]() $(U,V)$
into two regular cherries and then use Lemma 4.2 in each cherry. More precisely, we partition
$(U,V)$
into two regular cherries and then use Lemma 4.2 in each cherry. More precisely, we partition
![]() $V$
into
$V$
into
![]() $V_1$
,
$V_1$
,
![]() $U_2$
,
$U_2$
,
![]() $W_2$
and
$W_2$
and
![]() $U$
into
$U$
into
![]() $V_2$
,
$V_2$
,
![]() $U_1$
,
$U_1$
,
![]() $W_1$
such that for
$W_1$
such that for
![]() $i=1,2$
the pairs
$i=1,2$
the pairs
![]() $(U_i,V_i)$
and
$(U_i,V_i)$
and
![]() $(W_i,V_i)$
are
$(W_i,V_i)$
are
![]() $(\varepsilon ',d/4)$
-super-regular pairs and
$(\varepsilon ',d/4)$
-super-regular pairs and
![]() $(1-\delta _0)|V_i| \le |U_i|=|W_i| \le (1-\delta ) |V_i|$
. To obtain this, we split the sets according to the following random process. We put any vertex of
$(1-\delta _0)|V_i| \le |U_i|=|W_i| \le (1-\delta ) |V_i|$
. To obtain this, we split the sets according to the following random process. We put any vertex of
![]() $V$
into each of
$V$
into each of
![]() $U_2$
and
$U_2$
and
![]() $W_2$
with probability
$W_2$
with probability
![]() $q_1$
and into
$q_1$
and into
![]() $V_1$
with probability
$V_1$
with probability
![]() $1-2q_1$
. Similarly, we put any vertex of
$1-2q_1$
. Similarly, we put any vertex of
![]() $U$
into each of
$U$
into each of
![]() $U_1$
and
$U_1$
and
![]() $W_1$
with probability
$W_1$
with probability
![]() $q_2$
and into
$q_2$
and into
![]() $V_2$
with probability
$V_2$
with probability
![]() $1-2q_2$
. We choose
$1-2q_2$
. We choose
![]() $q_1$
and
$q_1$
and
![]() $q_2$
such that the expected sizes satisfy for
$q_2$
such that the expected sizes satisfy for
![]() $i=1,2$
$i=1,2$
This is possible since such conditions give a linear system of two equations in two variables
![]() $q_1$
and
$q_1$
and
![]() $q_2$
. As
$q_2$
. As
![]() $3n/4 \le n_0 \le n$
, the solution satisfies
$3n/4 \le n_0 \le n$
, the solution satisfies
![]() $1/7 \lt q_1,q_2 \lt 3/7$
. Then by Chernoff’s inequality (Lemma 3.1) and with
$1/7 \lt q_1,q_2 \lt 3/7$
. Then by Chernoff’s inequality (Lemma 3.1) and with
![]() $n$
large enough there exists a partition such that for
$n$
large enough there exists a partition such that for
![]() $i=1,2$
we have that
$i=1,2$
we have that
![]() $|W_i|$
,
$|W_i|$
,
![]() $|U_i|$
, and
$|U_i|$
, and
![]() $|V_i|$
are all within
$|V_i|$
are all within
![]() $\pm n^{2/3}$
of their expectation and the minimum degree within both pairs
$\pm n^{2/3}$
of their expectation and the minimum degree within both pairs
![]() $(U_i,V_i)$
and
$(U_i,V_i)$
and
![]() $(W_i,V_i)$
is at least a
$(W_i,V_i)$
is at least a
![]() $d/2$
-fraction of the other set. For
$d/2$
-fraction of the other set. For
![]() $i=1,2$
we redistribute
$i=1,2$
we redistribute
![]() $o(n)$
vertices between
$o(n)$
vertices between
![]() $U_i$
and
$U_i$
and
![]() $W_i$
and move at most one vertex from or to
$W_i$
and move at most one vertex from or to
![]() $V_i$
to obtain
$V_i$
to obtain
with minimum degree within both pairs
![]() $(U_i,V_i)$
and
$(U_i,V_i)$
and
![]() $(W_i,V_i)$
at least a
$(W_i,V_i)$
at least a
![]() $d/4$
-fraction of the other set.
$d/4$
-fraction of the other set.
From this we get that for
![]() $i=1,2$
the pairs
$i=1,2$
the pairs
![]() $(U_i,V_i)$
and
$(U_i,V_i)$
and
![]() $(W_i,V_i)$
are
$(W_i,V_i)$
are
![]() $(\varepsilon ',d/4)$
-super-regular. Also note that
$(\varepsilon ',d/4)$
-super-regular. Also note that
![]() $\min \{ |V_1|, |V_2|\} \ge \min \{ (1-2.1q_1)n, (1-2.1q_2)n_0 \} \ge n/10$
by the bound on
$\min \{ |V_1|, |V_2|\} \ge \min \{ (1-2.1q_1)n, (1-2.1q_2)n_0 \} \ge n/10$
by the bound on
![]() $q_1$
and
$q_1$
and
![]() $q_2$
from above. Then for
$q_2$
from above. Then for
![]() $i=1,2$
and with
$i=1,2$
and with
![]() $C/n \ge C'/ \min \{ |V_1|, |V_2|\}$
we a.a.s. get a triangle factor on
$C/n \ge C'/ \min \{ |V_1|, |V_2|\}$
we a.a.s. get a triangle factor on
![]() $V_i$
,
$V_i$
,
![]() $U_i$
,
$U_i$
,
![]() $W_i$
from Lemma 4.2. Together these give a triangle factor on
$W_i$
from Lemma 4.2. Together these give a triangle factor on
![]() $U \cup V$
.
$U \cup V$
.
9. Concluding remarks and open problems
In this paper, we close the last gap for the existence of a triangle factor in randomly perturbed graphs
![]() $G_\alpha \cup G(n,p)$
and now the threshold is determined for any
$G_\alpha \cup G(n,p)$
and now the threshold is determined for any
![]() $\alpha \in [0,1]$
(c.f. Table 1). In this last section, we would like to discuss a possible improvement for Theorem 2.4 and three different directions for generalisations of our results.
$\alpha \in [0,1]$
(c.f. Table 1). In this last section, we would like to discuss a possible improvement for Theorem 2.4 and three different directions for generalisations of our results.
9.1 Optimality of the sublinear theorem
The bound on
![]() $p$
in Theorem 1.3 is asymptotically optimal. However, as discussed earlier, when
$p$
in Theorem 1.3 is asymptotically optimal. However, as discussed earlier, when
![]() $m$
is significantly smaller than
$m$
is significantly smaller than
![]() $n/3$
, then
$n/3$
, then
![]() $K_{m,n-m} \cup G(n,p)$
contains
$K_{m,n-m} \cup G(n,p)$
contains
![]() $m$
pairwise vertex-disjoint triangles already at
$m$
pairwise vertex-disjoint triangles already at
![]() $p \ge C/n$
. When dealing with the sublinear case
$p \ge C/n$
. When dealing with the sublinear case
![]() $1 \le m \le n/256$
in Theorem 2.4, we require
$1 \le m \le n/256$
in Theorem 2.4, we require
![]() $p \ge C \log n/n$
; in fact we do not use the
$p \ge C \log n/n$
; in fact we do not use the
![]() $\log n$
-term when
$\log n$
-term when
![]() $(\log n)^3 \le m \le \sqrt{n}$
(notice indeed that Proposition 7.1 is stated with
$(\log n)^3 \le m \le \sqrt{n}$
(notice indeed that Proposition 7.1 is stated with
![]() $p \ge C/n$
). It would be interesting to understand if
$p \ge C/n$
). It would be interesting to understand if
![]() $p \ge C/n$
also suffices for larger values of
$p \ge C/n$
also suffices for larger values of
![]() $m$
and if Proposition 7.2 can be improved.
$m$
and if Proposition 7.2 can be improved.
Problem 9.1.
Show that there exists
![]() $C \gt 0$
such that for any
$C \gt 0$
such that for any
![]() $\sqrt{n} \le m \le n/32$
and any
$\sqrt{n} \le m \le n/32$
and any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with maximum degree
$G$
with maximum degree
![]() $\Delta (G) \le n/32$
and minimum degree
$\Delta (G) \le n/32$
and minimum degree
![]() $\delta (G)\ge m$
, a.a.s.
$\delta (G)\ge m$
, a.a.s.
![]() $G \cup G(n,p)$
contains
$G \cup G(n,p)$
contains
![]() $m$
pairwise vertex-disjoint triangles, provided
$m$
pairwise vertex-disjoint triangles, provided
![]() $p \ge C/n$
.
$p \ge C/n$
.
Note that this would improve Theorem 2.3 when
![]() $\alpha \lt 1/3$
. Indeed in our proof we only need the
$\alpha \lt 1/3$
. Indeed in our proof we only need the
![]() $\log n$
-term as we apply Theorem 2.4, while we could use Lemma 4.2 instead of 4.1 and avoid the
$\log n$
-term as we apply Theorem 2.4, while we could use Lemma 4.2 instead of 4.1 and avoid the
![]() $\log n$
-term in the rest of the argument.
$\log n$
-term in the rest of the argument.
9.2 Larger cliques
Similarly to a triangle factor, for any integer
![]() $r \ge 2$
and any
$r \ge 2$
and any
![]() $\alpha \in [0,1]$
, one can look at the threshold for the existence of a
$\alpha \in [0,1]$
, one can look at the threshold for the existence of a
![]() $K_r$
-factor in
$K_r$
-factor in
![]() $G_\alpha \cup G(n,p)$
. The result of Johannson, Kahn, and Vu [Reference Johansson, Kahn and Vu20] determines the threshold in
$G_\alpha \cup G(n,p)$
. The result of Johannson, Kahn, and Vu [Reference Johansson, Kahn and Vu20] determines the threshold in
![]() $G(n,p)$
at
$G(n,p)$
at
![]() $n^{-2/r} \log ^{2/(r^2-r)} n$
and for
$n^{-2/r} \log ^{2/(r^2-r)} n$
and for
![]() $\alpha \ge 1-1/r$
the existence in
$\alpha \ge 1-1/r$
the existence in
![]() $G_\alpha$
alone is proved by Hajnal-Szemerédi Theorem [Reference Hajnal and Szemerédi16]. For other values of
$G_\alpha$
alone is proved by Hajnal-Szemerédi Theorem [Reference Hajnal and Szemerédi16]. For other values of
![]() $\alpha$
, the results of Balogh, Treglown, and Wagner [Reference Balogh, Treglown and Wagner4] and of Han, Morris and Treglown [Reference Han, Morris and Treglown17] can be summarised in the following theorem generalising Theorem 1.2.
$\alpha$
, the results of Balogh, Treglown, and Wagner [Reference Balogh, Treglown and Wagner4] and of Han, Morris and Treglown [Reference Han, Morris and Treglown17] can be summarised in the following theorem generalising Theorem 1.2.
Theorem 9.2.
For any integers
![]() $2 \le k \le r$
and any
$2 \le k \le r$
and any
![]() $\alpha \in (1-\frac{k}{r}, 1-\frac{k-1}{r})$
there exists
$\alpha \in (1-\frac{k}{r}, 1-\frac{k-1}{r})$
there exists
![]() $C\gt 0$
such that the following holds. For any
$C\gt 0$
such that the following holds. For any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G) \ge \alpha n$
there a.a.s. is a
$\delta (G) \ge \alpha n$
there a.a.s. is a
![]() $K_r$
-factor in
$K_r$
-factor in
![]() $G \cup G(n,p)$
provided that
$G \cup G(n,p)$
provided that
![]() $p \ge C n^{-2/k}$
.
$p \ge C n^{-2/k}$
.
However, this leaves open the question for the threshold in the boundary cases, i.e. when
![]() $\alpha =1-k/r$
for
$\alpha =1-k/r$
for
![]() $2 \le k \le r-1$
. A natural extremal structure is given by the complete
$2 \le k \le r-1$
. A natural extremal structure is given by the complete
![]() $\lceil r/k \rceil$
-partite graph with
$\lceil r/k \rceil$
-partite graph with
![]() $\lfloor r/k \rfloor$
classes of size
$\lfloor r/k \rfloor$
classes of size
![]() $kn/r$
and possibly one class of size
$kn/r$
and possibly one class of size
![]() $(1-\lfloor r/k \rfloor k/r)n$
if
$(1-\lfloor r/k \rfloor k/r)n$
if
![]() $k \nmid r$
. This implies that to get a
$k \nmid r$
. This implies that to get a
![]() $K_r$
-factor in
$K_r$
-factor in
![]() $G_\alpha \cup G(n,p)$
, we need to cover all but
$G_\alpha \cup G(n,p)$
, we need to cover all but
![]() $\operatorname{polylog} n$
vertices of the sets of size
$\operatorname{polylog} n$
vertices of the sets of size
![]() $kn/r$
with vertex-disjoint copies of
$kn/r$
with vertex-disjoint copies of
![]() $K_k$
, i.e. the threshold is at least
$K_k$
, i.e. the threshold is at least
![]() $n^{-2/k} (\log n)^{2/\left (k^2-k\right )}$
. Surprisingly, this is not sufficient in the case when
$n^{-2/k} (\log n)^{2/\left (k^2-k\right )}$
. Surprisingly, this is not sufficient in the case when
![]() $r\gt 3$
and
$r\gt 3$
and
![]() $k \ne 2$
; in fact, for small
$k \ne 2$
; in fact, for small
![]() $\varepsilon$
, even
$\varepsilon$
, even
![]() $n^{-2/k+\varepsilon }$
is not sufficient.
$n^{-2/k+\varepsilon }$
is not sufficient.
We briefly explain the counterexample for
![]() $r=4$
and
$r=4$
and
![]() $k=3$
, by constructing an
$k=3$
, by constructing an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $\delta (G) \ge (1-3/4)n = n/4$
such that even for small
$\delta (G) \ge (1-3/4)n = n/4$
such that even for small
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $p \ge n^{-2/3+\varepsilon }$
, a.a.s. the graph
$p \ge n^{-2/3+\varepsilon }$
, a.a.s. the graph
![]() $G \cup G(n,p)$
does not contain a
$G \cup G(n,p)$
does not contain a
![]() $K_4$
-factor. Let
$K_4$
-factor. Let
![]() $0\lt \varepsilon \le 1/49$
,
$0\lt \varepsilon \le 1/49$
,
![]() $p \ge n^{-2/3+\varepsilon }$
, and
$p \ge n^{-2/3+\varepsilon }$
, and
![]() $n^{7 \varepsilon } \le m \le n^{1/7}$
. Then, for two sets
$n^{7 \varepsilon } \le m \le n^{1/7}$
. Then, for two sets
![]() $A$
and
$A$
and
![]() $B$
with
$B$
with
![]() $|A|=n/4-m$
and
$|A|=n/4-m$
and
![]() $|B|=3n/4+m$
, we let
$|B|=3n/4+m$
, we let
![]() $G$
be the
$G$
be the
![]() $n$
-vertex graph on
$n$
-vertex graph on
![]() $V(G)=A \cup B$
such that
$V(G)=A \cup B$
such that
![]() $A$
is an independent set,
$A$
is an independent set,
![]() $G[B]$
is given by
$G[B]$
is given by
![]() $|B|/(2m)$
disjoint copies of
$|B|/(2m)$
disjoint copies of
![]() $K_{m,m}$
, and any pair of vertices
$K_{m,m}$
, and any pair of vertices
![]() $(a,b)$
with
$(a,b)$
with
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
is an edge. Clearly,
$b \in B$
is an edge. Clearly,
![]() $G$
has minimum degree
$G$
has minimum degree
![]() $n/4$
. If
$n/4$
. If
![]() $G \cup G(n,p)$
contains a
$G \cup G(n,p)$
contains a
![]() $K_4$
-factor, since
$K_4$
-factor, since
![]() $A$
only contains
$A$
only contains
![]() $n/4-m$
vertices, at least
$n/4-m$
vertices, at least
![]() $m$
copies of
$m$
copies of
![]() $K_4$
must lie within
$K_4$
must lie within
![]() $B$
. However we claim that a.a.s. the perturbed graph
$B$
. However we claim that a.a.s. the perturbed graph
![]() $G \cup G(n,p)[B]$
contains less than
$G \cup G(n,p)[B]$
contains less than
![]() $m$
copies of
$m$
copies of
![]() $K_4$
and thus a.a.s.
$K_4$
and thus a.a.s.
![]() $G \cup G(n,p)$
does not contain a
$G \cup G(n,p)$
does not contain a
![]() $K_4$
-factor. Denote by
$K_4$
-factor. Denote by
![]() $X$
the number of
$X$
the number of
![]() $K_4$
’s in
$K_4$
’s in
![]() $G \cup G(n,p)[B]$
. It is not hard to see that when
$G \cup G(n,p)[B]$
. It is not hard to see that when
![]() $m$
is not too small the best way to build a
$m$
is not too small the best way to build a
![]() $K_4$
in
$K_4$
in
![]() $B$
is to choose a
$B$
is to choose a
![]() $K_{m,m}$
in
$K_{m,m}$
in
![]() $B$
and ask for an edge of
$B$
and ask for an edge of
![]() $G(n,p)$
on each side of
$G(n,p)$
on each side of
![]() $K_{m,m}$
. We get
$K_{m,m}$
. We get
![]() $\mathbb{E}[X] \lesssim \frac{n}{m} m^4 p^2 = o(m)$
and by Markov’s inequality a.a.s.
$\mathbb{E}[X] \lesssim \frac{n}{m} m^4 p^2 = o(m)$
and by Markov’s inequality a.a.s.
![]() $X \lt m$
as claimed.
$X \lt m$
as claimed.
Problem 9.3.
Determine the behaviour of the threshold and the extremal graphs at and around minimum degree
![]() $n/4$
.
$n/4$
.
The counterexamples for other values of
![]() $r\gt 3$
and
$r\gt 3$
and
![]() $k\ne 2$
can be constructed in a similar way, by slightly modifying the corresponding extremal graph defined above. In the case when
$k\ne 2$
can be constructed in a similar way, by slightly modifying the corresponding extremal graph defined above. In the case when
![]() $k=2$
, this construction does not increase the lower bound
$k=2$
, this construction does not increase the lower bound
![]() $n^{-1} \log n$
and, with Theorem 2.4 in mind, we believe that Theorem 1.4 generalises to
$n^{-1} \log n$
and, with Theorem 2.4 in mind, we believe that Theorem 1.4 generalises to
![]() $K_r$
. However, we believe that in all cases, using our methods, Theorem 2.2 can be extended to
$K_r$
. However, we believe that in all cases, using our methods, Theorem 2.2 can be extended to
![]() $K_r$
: i.e. for all
$K_r$
: i.e. for all
![]() $2 \le k \le r-1$
and with
$2 \le k \le r-1$
and with
![]() $\alpha =1-k/r$
, when
$\alpha =1-k/r$
, when
![]() $G_\alpha$
is not close (with a similar condition as in Definition 2.1) to the extremal graph defined above, then
$G_\alpha$
is not close (with a similar condition as in Definition 2.1) to the extremal graph defined above, then
![]() $p \ge C n^{-2/k}$
is sufficient for a
$p \ge C n^{-2/k}$
is sufficient for a
![]() $K_r$
-factor in
$K_r$
-factor in
![]() $G_\alpha \cup G(n,p)$
.
$G_\alpha \cup G(n,p)$
.
9.3 Longer cycles
Another possible generalisation is to consider factors of longer cycles
![]() $C_{\ell }$
. With slight adjustments to our methods (mainly to Theorem 2.4), we are able to show the following theorem.
$C_{\ell }$
. With slight adjustments to our methods (mainly to Theorem 2.4), we are able to show the following theorem.
Theorem 9.4.
For any integer
![]() $\ell \ge 3$
there exists
$\ell \ge 3$
there exists
![]() $C\gt 0$
such that for any
$C\gt 0$
such that for any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
we can a.a.s. find at least
$G$
we can a.a.s. find at least
![]() $\min \{ \delta (G), \lfloor n/\ell \rfloor \}$
pairwise vertex-disjoint
$\min \{ \delta (G), \lfloor n/\ell \rfloor \}$
pairwise vertex-disjoint
![]() $C_\ell$
’s in
$C_\ell$
’s in
![]() $G \cup G(n,p)$
, provided that
$G \cup G(n,p)$
, provided that
![]() $p\ge C \log n/n$
.
$p\ge C \log n/n$
.
We will discuss this in [Reference Böttcher, Parczyk, Sgueglia and Skokan9, Reference Böttcher, Parczyk, Sgueglia and Skokan10], including the corresponding variants for the finer statements, Theorems 2.2–2.4.
9.4 Universality
Even further, we call a graph
![]() $2$
-universal if it contains any
$2$
-universal if it contains any
![]() $n$
-vertex graph of maximum degree
$n$
-vertex graph of maximum degree
![]() $2$
as a subgraph. It is known that the threshold for
$2$
as a subgraph. It is known that the threshold for
![]() $2$
-universality is asymptotically the same as for a triangle factor when
$2$
-universality is asymptotically the same as for a triangle factor when
![]() $\alpha \lt 1/3$
or
$\alpha \lt 1/3$
or
![]() $\alpha \ge 2/3$
[Reference Aigner and Brandt1, Reference Ferber, Kronenberg and Luh15, Reference Parczyk28]. In a follow-up paper, we will expand our approach and prove that this also holds for the remaining cases, i.e.
$\alpha \ge 2/3$
[Reference Aigner and Brandt1, Reference Ferber, Kronenberg and Luh15, Reference Parczyk28]. In a follow-up paper, we will expand our approach and prove that this also holds for the remaining cases, i.e.
![]() $\log n/n$
gives the threshold for
$\log n/n$
gives the threshold for
![]() $\alpha =1/3$
and
$\alpha =1/3$
and
![]() $1/n$
gives the threshold when
$1/n$
gives the threshold when
![]() $1/3\lt \alpha \lt 2/3$
.
$1/3\lt \alpha \lt 2/3$
.
Acknowledgements
We thank an anonymous referee for the insightful and valuable comments.
A. Proof of Lemmas 3.2, 3.6, and 4.4
For the proof of Lemma 3.2 we use Janson’s inequality (see e.g. [Reference Janson, Łuczak and Ruciński19, Theorem 2.14]).
Lemma A.1.
Janson’s inequality Let
![]() $p \in (0,1)$
and consider a family
$p \in (0,1)$
and consider a family
![]() $\{ H_i \}_{i \in \mathcal{I}}$
of subgraphs of the complete graph on the vertex set
$\{ H_i \}_{i \in \mathcal{I}}$
of subgraphs of the complete graph on the vertex set
![]() $[n]=\{1,\ldots,n\}$
. For each
$[n]=\{1,\ldots,n\}$
. For each
![]() $i \in \mathcal{I}$
, let
$i \in \mathcal{I}$
, let
![]() $X_i$
denote the indicator random variable for the event that
$X_i$
denote the indicator random variable for the event that
![]() $H_i \subseteq G(n,p)$
and, write
$H_i \subseteq G(n,p)$
and, write
![]() $H_i \sim H_j$
for each ordered pair
$H_i \sim H_j$
for each ordered pair
![]() $(i,j) \in \mathcal{I} \times \mathcal{I}$
with
$(i,j) \in \mathcal{I} \times \mathcal{I}$
with
![]() $i \neq j$
if
$i \neq j$
if
![]() $E(H_i) \cap E(H_j) \not = \emptyset$
. Then, for
$E(H_i) \cap E(H_j) \not = \emptyset$
. Then, for
![]() $X = \sum _{i \in \mathcal{I}} X_i$
,
$X = \sum _{i \in \mathcal{I}} X_i$
,
![]() $\mathbb{E}[X] = \sum _{i \in \mathcal{I}} p^{e(H_i)}$
,
$\mathbb{E}[X] = \sum _{i \in \mathcal{I}} p^{e(H_i)}$
,
and any
![]() $0 \lt \gamma \lt 1$
we have
$0 \lt \gamma \lt 1$
we have
Proof of Lemma 3.2.Let
![]() $d\gt 0$
and pick
$d\gt 0$
and pick
![]() $C \gt 68/d^3$
and
$C \gt 68/d^3$
and
![]() $p\gt C/n$
. Let
$p\gt C/n$
. Let
![]() $\mathcal{I} = E_G(U,W) \times V$
and for each
$\mathcal{I} = E_G(U,W) \times V$
and for each
![]() $i=(uw,v) \in \mathcal{I}$
let
$i=(uw,v) \in \mathcal{I}$
let
![]() $H_i$
be the path
$H_i$
be the path
![]() $uvw$
on the three vertices
$uvw$
on the three vertices
![]() $u \in U$
,
$u \in U$
,
![]() $v \in V$
and
$v \in V$
and
![]() $w \in W$
. We want to apply Lemma A.1 to the family
$w \in W$
. We want to apply Lemma A.1 to the family
![]() $\{H_i\}_{i \in \mathcal{I}}$
. Using the same notation, we have
$\{H_i\}_{i \in \mathcal{I}}$
. Using the same notation, we have
![]() $\mathbb{E}[X] = |\mathcal{I}| p^2 \ge d n^3 p^2$
and
$\mathbb{E}[X] = |\mathcal{I}| p^2 \ge d n^3 p^2$
and
![]() $\delta \le n^2 (2n) n p^3$
, as for
$\delta \le n^2 (2n) n p^3$
, as for
![]() $i=(uw,v)$
and
$i=(uw,v)$
and
![]() $j=(u'w',v')$
with
$j=(u'w',v')$
with
![]() $i, j \in \mathcal{I}$
and
$i, j \in \mathcal{I}$
and
![]() $i \neq j$
we have
$i \neq j$
we have
![]() $H_i \sim H_j$
if and only if
$H_i \sim H_j$
if and only if
![]() $v=v'$
and precisely one of the equalities
$v=v'$
and precisely one of the equalities
![]() $u=u'$
and
$u=u'$
and
![]() $w=w'$
holds. Then the Janson’s inequality with
$w=w'$
holds. Then the Janson’s inequality with
![]() $\gamma =1/2$
gives
$\gamma =1/2$
gives
as
![]() $p\gt C/n$
and
$p\gt C/n$
and
![]() $C \gt 68/d^3$
. Thus with probability at least
$C \gt 68/d^3$
. Thus with probability at least
![]() $1-2^{-4n/d}$
we have
$1-2^{-4n/d}$
we have
![]() $X \gt \mathbb{E}[X]/2$
and there is at least one path
$X \gt \mathbb{E}[X]/2$
and there is at least one path
![]() $H_i$
on vertices
$H_i$
on vertices
![]() $u,v,w$
for some
$u,v,w$
for some
![]() $i=(uw,v) \in \mathcal{I}$
in
$i=(uw,v) \in \mathcal{I}$
in
![]() $G(n,p)$
. As
$G(n,p)$
. As
![]() $uw$
is an edge of
$uw$
is an edge of
![]() $G$
by definition of
$G$
by definition of
![]() $\mathcal{I}$
, we get a triangle in
$\mathcal{I}$
, we get a triangle in
![]() $G \cup G(U \cup W,V,p)$
with one vertex in each of
$G \cup G(U \cup W,V,p)$
with one vertex in each of
![]() $U,V,W$
, as required.
$U,V,W$
, as required.
Next, we prove that if a bipartite graph
![]() $G$
has large minimum degree, its random subgraph
$G$
has large minimum degree, its random subgraph
![]() $G_p$
contains a perfect matching if
$G_p$
contains a perfect matching if
![]() $p \ge C \log n/n$
.
$p \ge C \log n/n$
.
Proof of Lemma 3.6.For
![]() $\varepsilon \gt 0$
let
$\varepsilon \gt 0$
let
![]() $C \ge 3/\varepsilon$
. Let
$C \ge 3/\varepsilon$
. Let
![]() $G$
be a bipartite graph with partition classes
$G$
be a bipartite graph with partition classes
![]() $U$
and
$U$
and
![]() $W$
of size
$W$
of size
![]() $n$
and minimum degree at least
$n$
and minimum degree at least
![]() $(1/2+\varepsilon )n$
. Let
$(1/2+\varepsilon )n$
. Let
![]() $p \ge C \log n/n$
and suppose that
$p \ge C \log n/n$
and suppose that
![]() $G_p$
does not have a perfect matching. Then, by Hall’s Theorem, there exists a set
$G_p$
does not have a perfect matching. Then, by Hall’s Theorem, there exists a set
![]() $S \subseteq U$
or
$S \subseteq U$
or
![]() $S \subseteq W$
with
$S \subseteq W$
with
![]() $|S| \gt |N(S)|$
. Let
$|S| \gt |N(S)|$
. Let
![]() $S$
be a minimal such set, then
$S$
be a minimal such set, then
![]() $|S|=|N(S)|+1$
,
$|S|=|N(S)|+1$
,
![]() $|S| \leq \lceil n/2 \rceil$
, and every vertex in
$|S| \leq \lceil n/2 \rceil$
, and every vertex in
![]() $|N(S)|$
is adjacent to at least two vertices of
$|N(S)|$
is adjacent to at least two vertices of
![]() $S$
.
$S$
.
Let
![]() $1 \leq s \leq \lceil n/2 \rceil$
and let
$1 \leq s \leq \lceil n/2 \rceil$
and let
![]() $A_s$
denote the event that there is a minimal set
$A_s$
denote the event that there is a minimal set
![]() $S$
of size
$S$
of size
![]() $s$
violating Hall’s condition. If
$s$
violating Hall’s condition. If
![]() $s=1$
, then
$s=1$
, then
![]() $S$
is an isolated vertex. Let
$S$
is an isolated vertex. Let
![]() $X_n$
be the number of isolated vertices in
$X_n$
be the number of isolated vertices in
![]() $G_p$
, then for
$G_p$
, then for
![]() $n$
large enough
$n$
large enough
and
![]() $\lim _{n \rightarrow \infty } \mathbb{E}[X_n] = 0$
. Therefore, a.a.s.
$\lim _{n \rightarrow \infty } \mathbb{E}[X_n] = 0$
. Therefore, a.a.s.
![]() $G_p$
does not contain isolated vertices.
$G_p$
does not contain isolated vertices.
If
![]() $s \geq 2$
, then
$s \geq 2$
, then
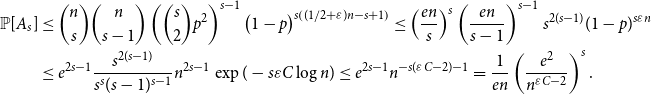 \begin{align*} \mathbb{P}[A_s] & \leq \binom{n}{s} \binom{n}{s-1} \left ( \binom{s}{2} p^2 \right )^{s-1} \left ( 1-p \right )^{s \left ( (1/2+\varepsilon ) n - s + 1 \right )} \leq \left ( \frac{en}{s} \right )^s \left ( \frac{en}{s-1} \right )^{s-1} s^{2(s-1)} (1-p)^{s \varepsilon n} \\ & \leq e^{2s-1} \frac{s^{2(s-1)}}{s^s (s-1)^{s-1}} n^{2s-1} \exp (-s \varepsilon C \log n) \leq e^{2s-1} n^{-s(\varepsilon C - 2) -1} = \frac{1}{e n} \left ( \frac{e^2}{n^{\varepsilon C -2}} \right )^s. \end{align*}
\begin{align*} \mathbb{P}[A_s] & \leq \binom{n}{s} \binom{n}{s-1} \left ( \binom{s}{2} p^2 \right )^{s-1} \left ( 1-p \right )^{s \left ( (1/2+\varepsilon ) n - s + 1 \right )} \leq \left ( \frac{en}{s} \right )^s \left ( \frac{en}{s-1} \right )^{s-1} s^{2(s-1)} (1-p)^{s \varepsilon n} \\ & \leq e^{2s-1} \frac{s^{2(s-1)}}{s^s (s-1)^{s-1}} n^{2s-1} \exp (-s \varepsilon C \log n) \leq e^{2s-1} n^{-s(\varepsilon C - 2) -1} = \frac{1}{e n} \left ( \frac{e^2}{n^{\varepsilon C -2}} \right )^s. \end{align*}
We have
The probability that there is a minimal set
![]() $S$
violating Hall’s condition is then bounded by
$S$
violating Hall’s condition is then bounded by
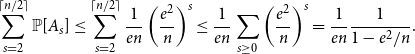 \begin{equation*} \sum _{s=2}^{\lceil n/2 \rceil } \mathbb {P}[A_s] \leq \sum _{s=2}^{\lceil n/2 \rceil } \frac {1}{e n} \left ( \frac {e^2}{n} \right )^s \leq \frac {1}{e n} \sum _{s \geq 0} \left ( \frac {e^2}{n} \right )^s = \frac {1}{e n} \frac {1}{1-e^2/n}.\end{equation*}
\begin{equation*} \sum _{s=2}^{\lceil n/2 \rceil } \mathbb {P}[A_s] \leq \sum _{s=2}^{\lceil n/2 \rceil } \frac {1}{e n} \left ( \frac {e^2}{n} \right )^s \leq \frac {1}{e n} \sum _{s \geq 0} \left ( \frac {e^2}{n} \right )^s = \frac {1}{e n} \frac {1}{1-e^2/n}.\end{equation*}
As
![]() $\lim _{n \rightarrow \infty } \frac{1}{e n} \frac{1}{1-e^2/n} = 0$
, a.a.s.
$\lim _{n \rightarrow \infty } \frac{1}{e n} \frac{1}{1-e^2/n} = 0$
, a.a.s.
![]() $G_p$
does not violate Hall’s condition and, therefore, contains a perfect matching.
$G_p$
does not violate Hall’s condition and, therefore, contains a perfect matching.
Finally we prove Lemma 4.4 following the argument of [Reference Balogh, Mousset and Skokan3, Lemma
![]() $12$
and
$12$
and
![]() $13$
]. For this we consider a largest matching
$13$
]. For this we consider a largest matching
![]() $M$
in the reduced graph
$M$
in the reduced graph
![]() $R$
and assume that
$R$
and assume that
![]() $|M|\lt (\alpha +2d)t$
. Then we will find a set
$|M|\lt (\alpha +2d)t$
. Then we will find a set
![]() $I \subseteq V(R)$
of size roughly
$I \subseteq V(R)$
of size roughly
![]() $(1-\alpha ) t$
which contains very few edges. With the properties of the reduced graph, we conclude that the original graph
$(1-\alpha ) t$
which contains very few edges. With the properties of the reduced graph, we conclude that the original graph
![]() $G$
is
$G$
is
![]() $(\alpha,\beta )$
-stable.
$(\alpha,\beta )$
-stable.
Proof of Lemma 4.4.Given
![]() $0\lt \beta \lt \tfrac{1}{12}$
let
$0\lt \beta \lt \tfrac{1}{12}$
let
![]() $0\lt d\lt 10^{-4} \beta ^6$
. Then let
$0\lt d\lt 10^{-4} \beta ^6$
. Then let
![]() $0\lt \varepsilon \lt d/4$
,
$0\lt \varepsilon \lt d/4$
,
![]() $4 \beta \le \alpha \le \tfrac 13$
, and
$4 \beta \le \alpha \le \tfrac 13$
, and
![]() $t \ge \tfrac{10}{d}$
. Next let
$t \ge \tfrac{10}{d}$
. Next let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph on vertex set
$n$
-vertex graph on vertex set
![]() $V$
with minimum degree
$V$
with minimum degree
![]() $\delta (G) \ge (\alpha -\tfrac 12 d)n$
that is not
$\delta (G) \ge (\alpha -\tfrac 12 d)n$
that is not
![]() $(\alpha,\beta )$
-stable and let
$(\alpha,\beta )$
-stable and let
![]() $R$
be the
$R$
be the
![]() $(\varepsilon,d)$
-reduced graph for some
$(\varepsilon,d)$
-reduced graph for some
![]() $(\varepsilon,d)$
-regular partition
$(\varepsilon,d)$
-regular partition
![]() $V_0,\dots,V_t$
of
$V_0,\dots,V_t$
of
![]() $G$
. We observe for the minimum degree of
$G$
. We observe for the minimum degree of
![]() $R$
that
$R$
that
![]() $\delta (R) \ge (\alpha -2d) t$
because, otherwise, there would be vertices with degree at most
$\delta (R) \ge (\alpha -2d) t$
because, otherwise, there would be vertices with degree at most
![]() $(\alpha -2d)t(n/t)+\varepsilon n \lt (\alpha - d/2)n - (d+\varepsilon )n$
in
$(\alpha -2d)t(n/t)+\varepsilon n \lt (\alpha - d/2)n - (d+\varepsilon )n$
in
![]() $G'$
contradicting (P2).
$G'$
contradicting (P2).
Let
![]() $M$
be a matching in
$M$
be a matching in
![]() $R$
of maximal size. Observe that
$R$
of maximal size. Observe that
![]() $|M| \ge \min \{ \delta (R),\lfloor t/2 \rfloor \} \ge (\alpha -2d)t$
. We assume
$|M| \ge \min \{ \delta (R),\lfloor t/2 \rfloor \} \ge (\alpha -2d)t$
. We assume
![]() $|M| \lt (\alpha +2d)t$
and show that
$|M| \lt (\alpha +2d)t$
and show that
![]() $G$
must then be
$G$
must then be
![]() $(\alpha,\beta )$
-stable, which is a contradiction. Let
$(\alpha,\beta )$
-stable, which is a contradiction. Let
![]() $U = V(R) \setminus V(M)$
. We shall first show that there exists a set
$U = V(R) \setminus V(M)$
. We shall first show that there exists a set
![]() $I \subseteq V(R)$
of size
$I \subseteq V(R)$
of size
![]() $|U|+|M|$
that contains only few egdes.
$|U|+|M|$
that contains only few egdes.
Since
![]() $M$
is a matching of maximal size in
$M$
is a matching of maximal size in
![]() $R$
,
$R$
,
![]() $U$
is independent. Moreover, given an edge
$U$
is independent. Moreover, given an edge
![]() $xy \in M$
, either
$xy \in M$
, either
![]() $x$
or
$x$
or
![]() $y$
has at most one neighbour in
$y$
has at most one neighbour in
![]() $U$
. Then we can split
$U$
. Then we can split
![]() $V(M)$
into two disjoint subsets
$V(M)$
into two disjoint subsets
![]() $X$
and
$X$
and
![]() $Y$
by placing for each matching edge
$Y$
by placing for each matching edge
![]() $xy$
of
$xy$
of
![]() $M$
one of its endpoints with at most one neighbour in
$M$
one of its endpoints with at most one neighbour in
![]() $U$
into the subset
$U$
into the subset
![]() $X$
, and the other endpoint into the subset
$X$
, and the other endpoint into the subset
![]() $Y$
. We claim that
$Y$
. We claim that
![]() $I= U \cup X$
contains only few edges. We have
$I= U \cup X$
contains only few edges. We have
![]() $e(U)=0$
,
$e(U)=0$
,
![]() $e(X,U) \le |X|$
, and we can upper bound
$e(X,U) \le |X|$
, and we can upper bound
![]() $e(X)$
as follows. Let
$e(X)$
as follows. Let
![]() $xy \in E(X)$
and denote by
$xy \in E(X)$
and denote by
![]() $x'$
and
$x'$
and
![]() $y'$
the vertices matched to
$y'$
the vertices matched to
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $M$
respectively. Then
$M$
respectively. Then
![]() $x', y' \in Y$
and either
$x', y' \in Y$
and either
![]() $x'$
or
$x'$
or
![]() $y'$
has at most one neighbour in
$y'$
has at most one neighbour in
![]() $U$
. Otherwise, there would be two distinct vertices
$U$
. Otherwise, there would be two distinct vertices
![]() $x'', y'' \in U$
such that
$x'', y'' \in U$
such that
![]() $x'x''$
and
$x'x''$
and
![]() $y'y''$
are edges of
$y'y''$
are edges of
![]() $R$
, and we could apply the rotation
$R$
, and we could apply the rotation
![]() $M \setminus \{xx',yy'\} \cup \{xy, x'x'',y'y''\}$
and get a larger matching, contradicting the maximality of
$M \setminus \{xx',yy'\} \cup \{xy, x'x'',y'y''\}$
and get a larger matching, contradicting the maximality of
![]() $M$
. Therefore,
$M$
. Therefore,
![]() $e(X) \le |X||Z|$
, where
$e(X) \le |X||Z|$
, where
![]() $Z=\{v \in Y| \deg (v,U) \lt 2 \}$
. Observe that
$Z=\{v \in Y| \deg (v,U) \lt 2 \}$
. Observe that
and
where we use that since
![]() $U$
is independent, a vertex in
$U$
is independent, a vertex in
![]() $U$
can have neighbours only in
$U$
can have neighbours only in
![]() $X$
and
$X$
and
![]() $Y$
. We get
$Y$
. We get
where the first inequality comes from the upper and lower bound on
![]() $e(Y,U)$
, the second one from
$e(Y,U)$
, the second one from
![]() $|Y| = |M| \lt (\alpha +2d)t$
and
$|Y| = |M| \lt (\alpha +2d)t$
and
![]() $\delta (R) \ge (\alpha -2d)t$
, and the last one from
$\delta (R) \ge (\alpha -2d)t$
, and the last one from
![]() $|U|=t-2|M| \ge t/4$
,
$|U|=t-2|M| \ge t/4$
,
![]() $|X| = |M| \lt t/2$
and
$|X| = |M| \lt t/2$
and
![]() $10/t \le d$
. Hence,
$10/t \le d$
. Hence,
![]() $e(X) \le |X| 5dt$
.
$e(X) \le |X| 5dt$
.
Therefore, the set
![]() $I=U \cup X$
has size
$I=U \cup X$
has size
because
![]() $|Y|=|M| = (\alpha \pm 2d)t$
and contains at most
$|Y|=|M| = (\alpha \pm 2d)t$
and contains at most
edges, where we use
![]() $|X|=|M| = (\alpha \pm 2d)t$
,
$|X|=|M| = (\alpha \pm 2d)t$
,
![]() $d \le \alpha/20$
and
$d \le \alpha/20$
and
![]() $10/t \le d$
in the last inequality.
$10/t \le d$
in the last inequality.
We now move to the original graph
![]() $G$
and prove that the existence of such set
$G$
and prove that the existence of such set
![]() $I$
in
$I$
in
![]() $R$
implies that
$R$
implies that
![]() $G$
is
$G$
is
![]() $(\alpha,\beta )$
-stable. Let
$(\alpha,\beta )$
-stable. Let
![]() $B''=\bigcup _{i \in I} V_i$
be the union of the clusters
$B''=\bigcup _{i \in I} V_i$
be the union of the clusters
![]() $I$
. Then
$I$
. Then
![]() $|B''| = (1-\alpha \pm 3d)n$
and
$|B''| = (1-\alpha \pm 3d)n$
and
![]() $e(B'') \le 6 \alpha dn^2$
. Let
$e(B'') \le 6 \alpha dn^2$
. Let
Then
![]() $e(B'') \ge (|B''|-|B'|) \sqrt{d} n$
and, therefore, all but at most
$e(B'') \ge (|B''|-|B'|) \sqrt{d} n$
and, therefore, all but at most
![]() $6 \alpha \sqrt{d}n$
vertices of
$6 \alpha \sqrt{d}n$
vertices of
![]() $B''$
belong to
$B''$
belong to
![]() $B'$
and, thus,
$B'$
and, thus,
![]() $|B'| = (1-\alpha \pm 4\sqrt{d})n$
. Let
$|B'| = (1-\alpha \pm 4\sqrt{d})n$
. Let
and note that
![]() $A'\cap B'=\emptyset$
. Observe that if
$A'\cap B'=\emptyset$
. Observe that if
![]() $v \in B'$
, then
$v \in B'$
, then
With
![]() $|V \setminus B'| \le (\alpha + 4 \sqrt{d})n$
this implies
$|V \setminus B'| \le (\alpha + 4 \sqrt{d})n$
this implies
and with the definition of
![]() $A'$
and the fact that
$A'$
and the fact that
![]() $|V \setminus (B' \cup A')| = |V \setminus B'| - |A'|$
, we get
$|V \setminus (B' \cup A')| = |V \setminus B'| - |A'|$
, we get
The last two inequalities imply that all but at most
![]() $24 \sqrt{d}n/\beta$
vertices of
$24 \sqrt{d}n/\beta$
vertices of
![]() $V \setminus B'$
belong to
$V \setminus B'$
belong to
![]() $A'$
. Therefore we can bound the size of
$A'$
. Therefore we can bound the size of
![]() $A'$
as follows
$A'$
as follows
and
where we used in both inequalities that
![]() $4 \sqrt{d}n + 24 \sqrt{d}n/\beta \le \beta ^2 n$
, as
$4 \sqrt{d}n + 24 \sqrt{d}n/\beta \le \beta ^2 n$
, as
![]() $d \le 10^{-4} \beta ^6$
.
$d \le 10^{-4} \beta ^6$
.
It follows that we have built two sets
![]() $A'$
and
$A'$
and
![]() $B'$
such that
$B'$
such that
![]() $|A' \cup B'| \ge n-\beta ^2 n$
,
$|A' \cup B'| \ge n-\beta ^2 n$
,
![]() $|A'| = \alpha n \pm \beta ^2 n$
and
$|A'| = \alpha n \pm \beta ^2 n$
and
![]() $|B'| = (1-\alpha )n \pm \beta ^2 n$
. Moreover each vertex of
$|B'| = (1-\alpha )n \pm \beta ^2 n$
. Moreover each vertex of
![]() $A'$
has at least
$A'$
has at least
![]() $(1-\beta/4)|B'|$
neighbours in
$(1-\beta/4)|B'|$
neighbours in
![]() $B'$
by the definition of
$B'$
by the definition of
![]() $A'$
, and each vertex of
$A'$
, and each vertex of
![]() $B'$
has at least
$B'$
has at least
![]() $(1-\beta/2)|A'|$
neighbours in
$(1-\beta/2)|A'|$
neighbours in
![]() $A'$
. This can be justified as follows. Given
$A'$
. This can be justified as follows. Given
![]() $v \in B'$
,
$v \in B'$
,
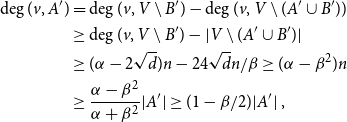 \begin{align*} \deg (v,A')&=\deg (v,V \setminus B') - \deg (v, V \setminus (A' \cup B')) \\ & \ge \deg (v,V \setminus B') - |V \setminus (A' \cup B')| \\ & \ge (\alpha - 2 \sqrt{d})n - 24\sqrt{d}n/\beta \ge (\alpha -\beta ^2)n\\ & \ge \frac{\alpha - \beta ^2}{\alpha + \beta ^2}|A'| \ge ( 1-\beta/2 ) |A'|\,, \end{align*}
\begin{align*} \deg (v,A')&=\deg (v,V \setminus B') - \deg (v, V \setminus (A' \cup B')) \\ & \ge \deg (v,V \setminus B') - |V \setminus (A' \cup B')| \\ & \ge (\alpha - 2 \sqrt{d})n - 24\sqrt{d}n/\beta \ge (\alpha -\beta ^2)n\\ & \ge \frac{\alpha - \beta ^2}{\alpha + \beta ^2}|A'| \ge ( 1-\beta/2 ) |A'|\,, \end{align*}
where we used that
![]() $A'$
and
$A'$
and
![]() $B'$
are disjoint, the inequalities (10),
$B'$
are disjoint, the inequalities (10),
![]() $|V \setminus (A' \cup B')| \le 24 \sqrt{d}n/\beta$
and
$|V \setminus (A' \cup B')| \le 24 \sqrt{d}n/\beta$
and
![]() $2 \sqrt{d}+ 24\sqrt{d}/\beta \le \beta ^2$
, the upper bound on
$2 \sqrt{d}+ 24\sqrt{d}/\beta \le \beta ^2$
, the upper bound on
![]() $|A'|$
and the inequality
$|A'|$
and the inequality
![]() $\alpha \ge 4 \beta$
.
$\alpha \ge 4 \beta$
.
Now we need to take care of the vertices of
![]() $G$
not yet covered by
$G$
not yet covered by
![]() $A' \cup B'$
, i.e. the at most
$A' \cup B'$
, i.e. the at most
![]() $\beta ^2 n$
vertices in
$\beta ^2 n$
vertices in
![]() $V \setminus (A' \cup B')$
. Let
$V \setminus (A' \cup B')$
. Let
![]() $v$
be one such vertex. Then
$v$
be one such vertex. Then
![]() $\deg (v,A' \cup B') \ge \delta (G) - |V \setminus (A' \cup B')| \ge (\alpha - d/2)n -\beta ^2 n \ge \alpha n/2$
. Therefore, it is possible to add these vertices to
$\deg (v,A' \cup B') \ge \delta (G) - |V \setminus (A' \cup B')| \ge (\alpha - d/2)n -\beta ^2 n \ge \alpha n/2$
. Therefore, it is possible to add these vertices to
![]() $A'$
and
$A'$
and
![]() $B'$
to obtain
$B'$
to obtain
![]() $A \supseteq A'$
and
$A \supseteq A'$
and
![]() $B \supseteq A'$
such that each vertex of
$B \supseteq A'$
such that each vertex of
![]() $B$
has at least
$B$
has at least
![]() $\alpha n/4$
neighbours in
$\alpha n/4$
neighbours in
![]() $A$
, and each vertex of
$A$
, and each vertex of
![]() $A$
has at least
$A$
has at least
![]() $\alpha n/4$
neighbours in
$\alpha n/4$
neighbours in
![]() $B$
. As we add at most
$B$
. As we add at most
![]() $\beta ^2 n$
vertices, we have
$\beta ^2 n$
vertices, we have
![]() $|A| = (\alpha \pm 2 \beta ^2) n$
and
$|A| = (\alpha \pm 2 \beta ^2) n$
and
![]() $|B| = (1-\alpha \pm 2\beta ^2)n$
. Moreover, all but at most
$|B| = (1-\alpha \pm 2\beta ^2)n$
. Moreover, all but at most
![]() $\beta ^2 n \le \beta n$
vertices from
$\beta ^2 n \le \beta n$
vertices from
![]() $A$
have degree at least
$A$
have degree at least
into
![]() $B$
, where we used that
$B$
, where we used that
![]() $|B| \le |B'|+\beta ^2 n$
,
$|B| \le |B'|+\beta ^2 n$
,
![]() $|B| \ge (1-\alpha -2\beta ^2)n \ge (2/3-2\beta ^2)n$
and
$|B| \ge (1-\alpha -2\beta ^2)n \ge (2/3-2\beta ^2)n$
and
![]() $\beta \lt 1/12$
. Similarly, all but at most
$\beta \lt 1/12$
. Similarly, all but at most
![]() $\beta ^2 n \le \beta n$
vertices from
$\beta ^2 n \le \beta n$
vertices from
![]() $B$
have degree at least
$B$
have degree at least
![]() $(1-\beta/2)|A'|\ge (1-\beta )|A|$
into
$(1-\beta/2)|A'|\ge (1-\beta )|A|$
into
![]() $A$
. Moreover, as
$A$
. Moreover, as
![]() $B'$
is a subset of
$B'$
is a subset of
![]() $B''$
and we add at most
$B''$
and we add at most
![]() $\beta ^2 n$
vertices to
$\beta ^2 n$
vertices to
![]() $B'$
to get
$B'$
to get
![]() $B$
, we have
$B$
, we have
![]() $e(B) \le e(B'') + \beta ^2 n^2 \le (6 \alpha d + \beta ^2)n^2 \le \beta n^2$
. Therefore,
$e(B) \le e(B'') + \beta ^2 n^2 \le (6 \alpha d + \beta ^2)n^2 \le \beta n^2$
. Therefore,
![]() $G$
is
$G$
is
![]() $(\alpha,\beta )$
-stable according to Definition 2.1.
$(\alpha,\beta )$
-stable according to Definition 2.1.