Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-18T20:11:00.838Z Has data issue: false hasContentIssue false
  • English
  • Français

Triangle-free subgraphs with large fractional chromatic number

Part of: Graph theory

Published online by Cambridge University Press:  29 June 2021

Bojan Mohar  and
Hehui Wu
Bojan Mohar*
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC, Canada
Hehui Wu
Affiliation:
Shanghai Center for Mathematical Sciences, Fudan University, Shanghai, China
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that for any integers k and g, there is a graph with chromatic number at least k and girth at least g. In 1960s, Erdös and Hajnal conjectured that for any k and g, there exists a number h(k,g), such that every graph with chromatic number at least h(k,g) contains a subgraph with chromatic number at least k and girth at least g. In 1977, Rödl proved the case when 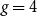$g=4$ , for arbitrary k. We prove the fractional chromatic number version of Rödl’s result.

Keywords

chromatic numberfractional chromatic numberErdös–Hajnal conjecture

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 136 - 143
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported in part by the NSERC Discovery Grant R611450 (Canada), by the Canada Research Chairs program, and by the Research Project J1-8130 of ARRS (Slovenia).

‡

Part of this work was done while the author was a PIMS Postdoctoral Fellow at the Department of Mathematics, Simon Fraser University, Burnaby, B.C.

References

Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers. J. Comb. Theory Ser. A 29 354–360.Google Scholar
Bollobás, B. and Sauer, N. (1976) Uniquely colourable graphs with large girth. Canad. J. Math. 28 1340–1344.CrossRefGoogle Scholar
Bukh, B. Interesting problems. http://www.borisbukh.org/problems.html. See also http://www.openproblemgarden. org/category/bukh_boris.Google Scholar
Dellamonica, D., Koubek, V., Martin, D. M. and Rödl, V. (2011) On a conjecture of Thomassen concerning subgraphs of large girth. J. Graph Theory 67 316–331.CrossRefGoogle Scholar
Dellamonica, D. and Rödl, V. (2011) A note on Thomassen’s conjecture. J. Comb. Theory Ser. B 101 509–515.Google Scholar
Erdös, P. (1959) Graph theory and probability. Canad. J. Math. 11(1) 34–38.CrossRefGoogle Scholar
Erdös, P. (1969) Problems and results in combinatorial analysis and graph theory. In Proof Techniques in Graph Theory (Harary, F., ed.), Academic Press, New York, pp. 27–35.Google Scholar
Godsil, C. and Royle, G. (2001) Algebraic Graph Theory. Springer-Verlag, New York.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2004) Every graph of sufficiently large average degree contains a $C_4$ -free subgraph of large average degree. Combinatorica 24 155–162.CrossRefGoogle Scholar
Kim, J. H. (1995) The Ramsey number R(3,t) has order of magnitude $t^2/\log t$ . Random Struct. Algorithms 7 173–207.Google Scholar
Lovász, L. (1978) Kneser’s conjecture, chromatic number, and homotopy. J. Comb. Theory Ser. A 25 319–324.CrossRefGoogle Scholar
Mohar, B. and Wu, H. (2016) Dichromatic number and fractional chromatic number. Forum Math. Sigma 4 e32, 14 p. https://doi.org/10.1017/fms.2016.28.CrossRefGoogle Scholar
Mohar, B. and Wu, H. (2020) Fractional chromatic number of a random subgraph. J. Graph Theory 95 467–472. https://doi.org/10.1002/jgt.22571.CrossRefGoogle Scholar
Pyber, L., Rödl, V. and Szemerédi, E. (1995) Dense graphs without 3-regular subgraphs. J. Combin. Theory Ser. B 63 41–54.CrossRefGoogle Scholar
Rödl, V. (1977) On the chromatic number of subgraphs of a given graph. Proc. Am. Math. Soc. 64 370–371.Google Scholar
Thomassen, C. (1983) Girth in graphs. J. Combin. Theory Ser. B 35 129–141.CrossRefGoogle Scholar
Zhu, X. (1996) Uniquely H-colorable graphs with large girth. J. Graph Theory 23 33–41.3.0.CO;2-L>CrossRefGoogle Scholar