Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T19:13:50.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Triangle-degrees in graphs and tetrahedron coverings in 3-graphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  09 September 2020

Victor Falgas-Ravry ,
Klas Markström  and
Yi Zhao
Victor Falgas-Ravry
Affiliation:
Department of Mathematics and Mathematical Statistics, Umeå Universitet, 901 87 Umeå, Sweden.
Klas Markström*
Affiliation:
Department of Mathematics and Mathematical Statistics, Umeå Universitet, 901 87 Umeå, Sweden.
Yi Zhao
Affiliation:
Department of Mathematics and Statistics, Georgia State University, Atlanta, GA30303, USA.
*
*Corresponding author. Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate a covering problem in 3-uniform hypergraphs (3-graphs): Given a 3-graph F, what is c1(n, F), the least integer d such that if G is an n-vertex 3-graph with minimum vertex-degree 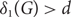$\delta_1(G)>d$ then every vertex of G is contained in a copy of F in G?

We asymptotically determine c1(n, F) when F is the generalized triangle 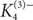$K_4^{(3)-}$ , and we give close to optimal bounds in the case where F is the tetrahedron 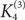$K_4^{(3)}$ (the complete 3-graph on 4 vertices).

This latter problem turns out to be a special instance of the following problem for graphs: Given an n-vertex graph G with 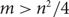$m> n^2/4$ edges, what is the largest t such that some vertex in G must be contained in t triangles? We give upper bound constructions for this problem that we conjecture are asymptotically tight. We prove our conjecture for tripartite graphs, and use flag algebra computations to give some evidence of its truth in the general case.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C65: Hypergraphs 05D99: None of the above, but in this section
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 2 , March 2021 , pp. 175 - 199
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Andrásfai, B., Erdős, P. and Sós, V. T. (1974) On the connection between chromatic number, maximal clique and minimal degree of a graph. Discrete Math. 8 205–218.CrossRefGoogle Scholar
Baber, R., Johnson, J. R. and Talbot, J. (2010) The minimal density of triangles in tripartite graphs. LMS J. Comput. Math. 13 388–413.CrossRefGoogle Scholar
Baber, R. and Talbot, J. (2012) New Turán densities for 3-graphs. Electron. J. Combin. 19 1–21.CrossRefGoogle Scholar
Bollobás, B. (1974) Three-graphs without two triples whose symmetric difference is contained in a third. Discrete Math. 8 21–24.CrossRefGoogle Scholar
Bollobás, B. (1976) On complete subgraphs of different orders. Math. Proc. Cambridge Philos. Soc. 79 19–24.CrossRefGoogle Scholar
Bollobás, B. and Nikiforov, V. (2005) Books in graphs. Europ. J. Combin. 26 259–270.CrossRefGoogle Scholar
Bondy, A., Shen, J., Thomassé, S. and Thomassen, C. (2006) Density conditions for triangles in multipartite graphs. Combinatorica 26 121–131.CrossRefGoogle Scholar
Colbourn, C. J., Forbes, A. D., Grannell, M. J., Griggs, T. S., Kaski, P., Östergård, P. R. J., Pike, D. A. and Pottonen, O. (2010) Properties of the Steiner triple systems of order 19. Electron. J. Combin. 17 1–30.CrossRefGoogle Scholar
Czygrinow, A. (2016) Tight co-degree condition for packing of loose cycles in 3-graphs. J. Graph Theory 83 317–333.CrossRefGoogle Scholar
Czygrinow, A., DeBiasio, L. and Nagle, B. (2014) Tiling 3-uniform hypergraphs with $K_4^3$ − 2e. J. Graph Theory 75 124–136.CrossRefGoogle Scholar
Czygrinow, A. and Nagle, B. (2001) A note on codegree problems for hypergraphs. Bull. Inst. Combin. Appl. 32 63–69.Google Scholar
De Caen, D. and Füredi, Z. (2000) The maximum size of 3-uniform hypergraphs not containing a Fano plane. J. Combin. Theory Ser. B 78 274–276.CrossRefGoogle Scholar
Edwards, C. S. (1977) A lower bound for the largest number of triangles with a common edge. Unpublished manuscript.Google Scholar
Erdős, P. (1962) On a theorem of Rademacher–Turán. Illinois J. Math 6 1–3.CrossRefGoogle Scholar
Erdős, P., Faudree, R. and Györi, E. (1995) On the book size of graphs with large minimum degree. Studia Sci. Math. Hungar. 30 25–46.Google Scholar
Erdős, P., Faudree, R. J. and Rousseau, C. C. (1994) Extremal problems and generalized degrees. Discrete Math. 127 139–152.CrossRefGoogle Scholar
Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc 52 1.CrossRefGoogle Scholar
Falgas-Ravry, V., Marchant, E., Pikhurko, O. and Vaughan, E. R. (2015) The codegree threshold for 3-graphs with independent neighborhoods. SIAM J. Discrete Math. 29 1504–1539.CrossRefGoogle Scholar
Falgas-Ravry, V., Pikhurko, O., Vaughan, E. and Volec, J. (2017) The codegree threshold of $K_4^-$ . Preprint.CrossRefGoogle Scholar
Falgas-Ravry, V. and Vaughan, E. R. (2013) Applications of the semi-definite method to the Turán density problem for 3-graphs. Combin. Probab. Comput. 22 21–54.CrossRefGoogle Scholar
Falgas-Ravry, V. and Zhao, Y. (2016) Codegree thresholds for covering 3-uniform hypergraphs. SIAM J. Discrete Math. 30 1899–1917.CrossRefGoogle Scholar
Fisher, D. C. (1989) Lower bounds on the number of triangles in a graph. J. Graph Theory 13 505–512.CrossRefGoogle Scholar
Füredi, Z. (1991) Turán type problems. In Surveys in Combinatorics 1991, Vol. 166 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 253–300.Google Scholar
Füredi, Z., Pikhurko, O. and Simonovits, M. (2005) On triple systems with independent neighbourhoods. Combin. Probab. Comput. 14 795–813.CrossRefGoogle Scholar
Gao, W. and Han, J. (2017) Minimum codegree threshold for $C_6^3$ -factors in 3-uniform hypergraphs. Combin. Probab. Comput. 26 536–559.CrossRefGoogle Scholar
Gao, W., Han, J. and Zhao, Y. (2019) Codegree conditions for tiling complete k-partite k-graphs and loose cycles. Combin. Probab. Comput. 28 840–870. doi: 10.1017/S096354831900021X CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of Erdős. Combin. Theory Appl. 2 601–623.Google Scholar
Hàn, H., Person, Y. and Schacht, M. (2009) On perfect matchings in uniform hypergraphs with large minimum vertex degree. SIAM J. Discrete Math 23 732–748.CrossRefGoogle Scholar
Han, J., Lo, A. and Sanhueza-Matamala, N. (2017) Covering and tiling hypergraphs with tight cycles. Electron. Notes Discret. Math. 61 561–567.CrossRefGoogle Scholar
Han, J., Lo, A., Treglown, A. and Zhao, Y. (2017) Exact minimum codegree threshold for $K_4^-$ -factors. Combin. Probab. Comput. 26 856–885. doi: 10.1017/S0963548317000268 CrossRefGoogle Scholar
Han, J., Zang, C. and Zhao, Y. (2017) Minimum vertex degree thresholds for tiling complete 3-partite 3-graphs. J. Combin. Theory Ser. A 149 115–147.CrossRefGoogle Scholar
Han, J. and Zhao, Y. (2015) Minimum vertex degree threshold for $C_4^3$ -tiling. J. Graph Theory 79 300–317.CrossRefGoogle Scholar
Kaski, P. and Östergård, P. R. J. (2006) Classification Algorithms for Codes and Designs, Vol. 15 of Algorithms and Computation in Mathematics, Springer.Google Scholar
Keevash, P. (2011) Hypergraph Turán problems. In Surveys in Combinatorics 2011, Vol. 392 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 83–139.Google Scholar
Keevash, P. and Mycroft, R. (2014) A Geometric Theory for Hypergraph Matching, Vol. 233, no. 1908, of Memoirs of the American Mathematical Society, American Mathematical Society.Google Scholar
Keevash, P. and Zhao, Y. (2007) Codegree problems for projective geometries. J. Combin. Theory Ser. B 97 919–928.CrossRefGoogle Scholar
Khadžiivanov, N. and Nikiforov, V. (1979) Solution of a problem of P. Erdős about the maximum number of triangles with a common edge in a graph (in Russian). C.R. Acad. Bulgare Sci. 32 1315–1318.Google Scholar
Khan, I. (2013) Perfect matchings in 3-uniform hypergraphs with large vertex degree. SIAM J. Discrete Math. 27 1021–1039.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2006) Loose Hamilton cycles in 3-uniform hypergraphs of high minimum degree. J. Combin. Theory Ser. B 96 767–821.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2009) The minimum degree threshold for perfect graph packings. Combinatorica 29 65–107.CrossRefGoogle Scholar
Kühn, D., Osthus, D. and Treglown, A. (2013) Matchings in 3-uniform hypergraphs. J. Combin. Theory Ser. B 103 291–305.CrossRefGoogle Scholar
Lo, A. (2012) Cliques in graphs with bounded minimum degree. Combin. Probab. Comput. 21 457–482.CrossRefGoogle Scholar
Lo, A. and Markström, K. (2013) Minimum codegree threshold for $(K_4- e)$ -factors. J. Combin. Theory Ser. A 120 708–721.CrossRefGoogle Scholar
Lo, A. and Markström, K. (2014) l-degree Turán Density. SIAM J. Discrete Math. 28 1214–1225.CrossRefGoogle Scholar
Lo, A. and Markström, K. (2015) F-factors in hypergraphs via absorption. Graphs Combin. 31 679–712.CrossRefGoogle Scholar
Lovász, L. and Simonovits, M. (1976) On the number of complete subgraphs of a graph. In Proceedings of the Fifth British Combinatorial Conference (Aberdeen 1975), pp. 431–441.Google Scholar
Lovász, L. and Simonovits, M. (1983) On the number of complete subgraphs of a graph II. In Studies in Pure Mathematics (Erdős, P. et al., eds), Birkhäuser, pp. 459–495.CrossRefGoogle Scholar
Mathon, R. A., Phelps, K. T. and Rosa, A. (1982) Small Steiner triple systems and their properties. Ars Combin. 15 3–110.Google Scholar
Mubayi, D. (2005) The co-degree density of the Fano plane. J. Combin. Theory Ser. B 95 333–337.CrossRefGoogle Scholar
Mubayi, D. and Rödl, V. (2002) On the Turán number of triple systems. J. Combin. Theory Ser. A 100 136–152.CrossRefGoogle Scholar
Mubayi, D. and Zhao, Y. (2007) Co-degree density of hypergraphs. J. Combin. Theory Ser. A 114 1118–1132.CrossRefGoogle Scholar
Mycroft, R. (2016) Packing k-partite k-uniform hypergraphs. J. Combin. Theory Ser. A 138 60–132.CrossRefGoogle Scholar
Nikiforov, V. (2011) The number of cliques in graphs of given order and size. Trans. Amer. Math. Soc. 363 1599–1618.CrossRefGoogle Scholar
Pikhurko, O. and Razborov, A. (2017) Asymptotic structure of graphs with the minimum number of triangles. Combin. Probab. Comput. 26 138–160.CrossRefGoogle Scholar
Razborov, A. (2007) Flag algebras. J. Symbolic Logic 72 1239–1282.CrossRefGoogle Scholar
Razborov, A. (2008) On the minimal density of triangles in graphs. Combin. Probab. Comput. 17 603–618.CrossRefGoogle Scholar
Razborov, A. A. (2013) Flag algebras: An interim report. In The Mathematics of Paul Erdős II (Graham, R. et al., eds), Springer, pp. 207–232.CrossRefGoogle Scholar
Reiher, C. (2016) The clique density theorem. Ann. of Math. 184 683–707.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A. (2010) Dirac-type questions for hypergraphs: A survey (or more problems for Endre to solve). In An Irregular Mind, Vol. 21 of Bolyai Society Mathematical Studies, Springer, pp. 561–590.Google Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2009) Perfect matchings in large uniform hypergraphs with large minimum collective degree. J. Combin. Theory Ser. A 116 613–636.CrossRefGoogle Scholar
Sidorenko, A. (1995) What we know and what we do not know about Turán numbers. Graphs Combin. 11 179–199.CrossRefGoogle Scholar
Sliacan, J. (2018) Flagmatic 2.0. https://github.com/jsliacan/flagmatic-2.0.Google Scholar
Turán, P. (1941) On an extremal problem in graph theory (in Hungarian). Mat. Fiz. Lapok 48 436–452.Google Scholar
Zhao, Y. (2016) Recent advances on Dirac-type problems for hypergraphs. In Recent Trends in Combinatorics, Vol. 159 of The IMA Volumes in Mathematics and its Applications, Springer, pp. 145–165.CrossRefGoogle Scholar