Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:00:21.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Tight Hamilton cycles in cherry-quasirandom 3-uniform hypergraphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  12 October 2020

Elad Aigner-Horev  and
Gil Levy
Elad Aigner-Horev*
Affiliation:
Department of Mathematics and Computer Science, Ariel University, Israel
Gil Levy
Affiliation:
Department of Mathematics and Computer Science, Ariel University, Israel
*
*Corresponding author. Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We employ the absorbing-path method in order to prove two results regarding the emergence of tight Hamilton cycles in the so-called two-path or cherry-quasirandom 3-graphs.

Our first result asserts that for any fixed real α > 0, cherry-quasirandom 3-graphs of sufficiently large order n having minimum 2-degree at least α(n – 2) have a tight Hamilton cycle.

Our second result concerns the minimum 1-degree sufficient for such 3-graphs to have a tight Hamilton cycle. Roughly speaking, we prove that for every d, α > 0 satisfying d + α > 1, any sufficiently large n-vertex such 3-graph H of density d and minimum 1-degree at least 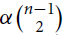$\alpha \left({\matrix{{n - 1} \cr 2 \cr } } \right)$ has a tight Hamilton cycle.

MSC classification

Primary: 05C35: Extremal problems 05C65: Hypergraphs
Secondary: 05C80: Random graphs 05D05: Extremal set theory 05C42: Density (toughness, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 3 , May 2021 , pp. 412 - 443
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Aigner-Horev, E., Conlon, D., Hàn, H., Person, Y. and Schacht, M. (2018) Quasirandomness in hypergraphs. Electron. J. Combin. 25 #3.34.Google Scholar
Araújo, P., Piga, S. and Schacht, M. (2019) Localised codegree conditions for tight Hamiltonian cycles in 3-uniform hypergraphs. Acta Math. Univ. Comenian. 88 389–394.Google Scholar
Blakley, G. R. and Roy, P. (1965) A Hölder type inequality for symmetric matrices with nonnegative entries. Proc. Amer. Math. Soc. 16 1244–1245.Google Scholar
Buß, E., Hàn, H. and Schacht, M. (2013) Minimum vertex degree conditions for loose Hamilton cycles in 3-uniform hypergraphs. J. Combin. Theory Ser. B 103 658–678.CrossRefGoogle Scholar
Chung, F. R. K., Graham, R. L. and Wilson, R. M. (1989) Quasi-random graphs. Combinatorica 9 345–362.CrossRefGoogle Scholar
Conlon, D., Hàn, H., Person, Y. and Schacht, M. (2012) Weak quasi-randomness for uniform hypergraphs. Random Struct. Algorithms 40 1–38.CrossRefGoogle Scholar
Cooley, O. and Mycroft, R. (2017) The minimum vertex degree for an almost-spanning tight cycle in a 3-uniform hypergraph. Discrete Math. 340 1172–1179.Google Scholar
De Oliveira Bastos, J., Mota, G. O., Schacht, M., Schnitzer, J. and Schulenburg, F. (2017) Loose Hamiltonian cycles forced by large (k – 2)-degree: approximate version. SIAM J. Discrete Math. 31 2328–2347.CrossRefGoogle Scholar
De Oliveira Bastos, J., Mota, G. O., Schacht, M., Schnitzer, J. and Schulenburg, F. (2018) Loose Hamiltonian cycles forced by large (k – 2)-degree: sharp version. Contrib. Discrete Math. 13 88–100.Google Scholar
Diestel, R. (2010) Graph Theory, fourth edition, Vol. 173 of Graduate Texts in Mathematics. Springer.Google Scholar
Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. London Math. Soc. (3) 2 69–81.CrossRefGoogle Scholar
Erdös, P. and Simonovits, M. (1984) Cube-supersaturated graphs and related problems. In Progress in Graph Theory (Waterloo, Ont., 1982) (Bondy, J. A. and Murty, U. S. R., eds), pp. 203–218. Academic Press.Google Scholar
Glebov, R., Person, Y. and Weps, W. (2012) On extremal hypergraphs for Hamiltonian cycles. European J. Combin. 33 544–555.CrossRefGoogle Scholar
Hàn, H. and Schacht, M. (2010) Dirac-type results for loose Hamilton cycles in uniform hypergraphs. J. Combin. Theory Ser. B 100 332–346.Google Scholar
Han, J. and Zhao, Y. (2015) Minimum codegree threshold for Hamilton ℓ-cycles in k-uniform hypergraphs. J. Combin. Theory Ser. A 132 194–223.CrossRefGoogle Scholar
Han, J. and Zhao, Y. (2015) Minimum vertex degree threshold for loose Hamilton cycles in 3-uniform hypergraphs. J. Combin. Theory Ser. B 114 70–96.CrossRefGoogle Scholar
Han, J. and Zhao, Y. (2016) Forbidding Hamilton cycles in uniform hypergraphs. J. Combin. Theory Ser. A 143 107–115.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization. Wiley-Interscience.Google Scholar
Katona, G. Y. and Kierstead, H. A. (1999) Hamiltonian chains in hypergraphs. J. Graph Theory 30 205–212.3.0.CO;2-O>CrossRefGoogle Scholar
Keevash, P., Kühn, D., Mycroft, R. and Osthus, D. (2011) Loose Hamilton cycles in hypergraphs. Discrete Math. 311 544–559.CrossRefGoogle Scholar
Krivelevich, M. and Sudakov, B. (2006) Pseudo-random graphs. In More Sets, Graphs and Numbers, Vol. 15 of Bolyai Society Mathematical Studies, pp. 199–262. Springer.Google Scholar
Kühn, D., Mycroft, R. and Osthus, D. (2010) Hamilton ℓ-cycles in uniform hypergraphs. J. Combin. Theory Ser. A 117 910–927.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2006) Loose Hamilton cycles in 3-uniform hypergraphs of high minimum degree. J. Combin. Theory Ser. B 96 767–821.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2014) Hamilton cycles in graphs and hypergraphs: an extremal perspective. In Proceedings of the International Congress of Mathematicians 2014, Seoul, Korea, pp. 381–406.Google Scholar
Lenz, J. and Mubayi, D. (2015) Eigenvalues and linear quasirandom hypergraphs. Forum Math. Sigma 3 e2, 26.Google Scholar
Lenz, J. and Mubayi, D. (2015) The poset of hypergraph quasirandomness. Random Struct. Algorithms 46 762–800.Google Scholar
Lenz, J., Mubayi, D. and Mycroft, R. (2016) Hamilton cycles in quasirandom hypergraphs. Random Struct. Algorithms 49 363–378.CrossRefGoogle Scholar
Reiher, C., Rödl, V. and Schacht, M. (2016) Embedding tetrahedra into quasirandom hypergraphs. J. Combin. Theory Ser. B 121 229–247.Google Scholar
Reiher, C., Rödl, V. and Schacht, M. (2018) Some remarks on πɅ. In Connections in discrete mathematics, pp. 214–239. Cambridge University Press.Google Scholar
Reiher, C., Rödl, V., Rucińki, A., Schacht, M. and Szemerédi, E. (2019) Minimum vertex degree condition for tight Hamiltonian cycles in 3-uniform hypergraphs. Proc. Lond. Math. Soc. (3) 119 409–439.CrossRefGoogle Scholar
Reiher, C. and Schacht, M. Private communication.Google Scholar
Rödl, V. and Ruciński, A. (2010) Dirac-type questions for hypergraphs: a survey (or more problems for Endre to solve). In An Irregular Mind, Vol. 21 of Bolyai Society Mathematical Studies, pp. 561–590. János Bolyai Mathematical Society.Google Scholar
Rödl, V. and Ruciński, A. (2014) Families of triples with high minimum degree are Hamiltonian. Discuss. Math. Graph Theory 34 361–381.CrossRefGoogle Scholar
Rödl, V., Ruciński, A., Schacht, M. and Szemerédi, E. (2017) On the Hamiltonicity of triple systems with high minimum degree. Ann. Combin. 21 95–117.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2006) A Dirac-type theorem for 3-uniform hypergraphs. Combin. Probab. Comput. 15 229–251.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2008) An approximate Dirac-type theorem for k-uniform hypergraphs. Combinatorica 28 229–260.Google Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2009) Perfect matchings in large uniform hypergraphs with large minimum collective degree. J. Combin. Theory Ser. A 116 613–636.Google Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2011) Dirac-type conditions for Hamiltonian paths and cycles in 3-uniform hypergraphs. Adv. Math. 227 1225–1299.CrossRefGoogle Scholar
Sidorenko, A. F. (1986) Extremal problems in graph theory and functional-analytic inequalities. In Proceedings of the All-Union Seminar on Discrete Mathematics and its Applications (Moscow, 1984), pp. 99–105 (in Russian). Moskov. Gos. Univ., Mekh.-Mat. Fak.Google Scholar
Szemerédi, E. (1978) Regular partitions of graphs. In Problèmes Combinatoires et Théorie des Graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), Vol. 260 of Colloq. Internat. CNRS, pp. 399–401. CNRS.Google Scholar
Thomason, A. (1987) Pseudorandom graphs. In Random Graphs ’85 (Poznań, 1985), Vol. 144 of North-Holland Mathematics Studies, pp. 307–331. North-Holland.Google Scholar
Thomason, A. (1987) Random graphs, strongly regular graphs and pseudorandom graphs. In Surveys in Combinatorics 1987 (New Cross, 1987), Vol. 123 of London Mathematical Society Lecture Note Series, pp. 173–195. Cambridge University Press.Google Scholar
Towsner, H. (2017) σ-algebras for quasirandom hypergraphs. Random Struct. Algorithms 50 114–139.Google Scholar
Zhao, Y. (2016) Recent advances on Dirac-type problems for hypergraphs. In Recent Trends in Combinatorics, Vol. 159 of IMA Volumes in Mathematics and its Applications, pp. 145–165. Springer.CrossRefGoogle Scholar