Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
2000.
Random Graphs.
p.
307.
Alon, N.
Capalbo, M.
Kohayakawa, Y.
Rodl, V.
Rucinski, A.
and
Szemeredi, E.
2000.
Universality and tolerance.
p.
14.
Kim, Jeong Han
2003.
Perfect matchings in random uniform hypergraphs.
Random Structures & Algorithms,
Vol. 23,
Issue. 2,
p.
111.
Haber, Simi
and
Krivelevich, Michael
2007.
On fractional K‐factors of random graphs.
Random Structures & Algorithms,
Vol. 30,
Issue. 4,
p.
441.
Yuster, Raphael
2007.
Combinatorial and computational aspects of graph packing and graph decomposition.
Computer Science Review,
Vol. 1,
Issue. 1,
p.
12.
Johansson, Anders
Kahn, Jeff
and
Vu, Van
2008.
Factors in random graphs.
Random Structures & Algorithms,
Vol. 33,
Issue. 1,
p.
1.
Yan, Yun-Zhi
Wang, Han-Xing
Wang, Jun
and
Yin, Xiang-Feng
2008.
-factors in random graphs.
Statistics & Probability Letters,
Vol. 78,
Issue. 11,
p.
1255.
Mennink, Bart
2012.
Increasing the flexibility of the herding attack.
Information Processing Letters,
Vol. 112,
Issue. 3,
p.
98.
BALOGH, JÓZSEF
LEE, CHOONGBUM
and
SAMOTIJ, WOJCIECH
2012.
Corrádi and Hajnal's Theorem for Sparse Random Graphs.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 1-2,
p.
23.
Karoński, Michał
and
Ruciński, Andrzej
2013.
The Mathematics of Paul Erdős I.
p.
371.
Gerke, Stefanie
and
McDowell, Andrew
2015.
Nonvertex‐Balanced Factors in Random Graphs.
Journal of Graph Theory,
Vol. 78,
Issue. 4,
p.
269.
Böttcher, Julia
2017.
Surveys in Combinatorics 2017.
p.
87.
BALOGH, JÓZSEF
TREGLOWN, ANDREW
and
WAGNER, ADAM ZSOLT
2019.
Tilings in Randomly Perturbed Dense Graphs.
Combinatorics, Probability and Computing,
Vol. 28,
Issue. 2,
p.
159.
Albin, Nathan
Clemens, Jason
Hoare, Derek
Poggi-Corradini, Pietro
Sit, Brandon
and
Tymochko, Sarah
2021.
Fairest edge usage and minimum expected overlap for random spanning trees.
Discrete Mathematics,
Vol. 344,
Issue. 5,
p.
112282.
Grechuk, Bogdan
2021.
Landscape of 21st Century Mathematics.
p.
255.
Riordan, Oliver
2022.
Random cliques in random graphs and sharp thresholds for F$$ F $$‐factors.
Random Structures & Algorithms,
Vol. 61,
Issue. 4,
p.
619.
Heckel, Annika
Kaufmann, Marc
Müller, Noela
and
Pasch, Matija
2023.
The hitting time of clique factors.
p.
552.
Demidovich, Yury
Skorkin, Arkadiy
and
Zhukovskii, Maksim
2023.
Cycle Saturation in Random Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 37,
Issue. 3,
p.
1359.
Heckel, Annika
Kaufmann, Marc
Müller, Noela
and
Pasch, Matija
2024.
The hitting time of clique factors.
Random Structures & Algorithms,
Vol. 65,
Issue. 2,
p.
275.
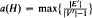 , where the maximum is taken over all subgraphs (V′, E′) of H with |V′| > 1. Let δ(H) denote the minimum degree of a vertex of H. It is shown that if δ(H) < a(H), then n−1/a(H) is a sharp threshold function for the property that the random graph G(n, p) contains an H-factor. That is, there are two positive constants c and C so that for p(n) = cn−1/a(H) almost surely G(n, p(n)) does not have an H-factor, whereas for p(n) = Cn−1/a(H), almost surely G(n, p(n)) contains an H-factor (provided h divides n). A special case of this answers a problem of Erdős.
, where the maximum is taken over all subgraphs (V′, E′) of H with |V′| > 1. Let δ(H) denote the minimum degree of a vertex of H. It is shown that if δ(H) < a(H), then n−1/a(H) is a sharp threshold function for the property that the random graph G(n, p) contains an H-factor. That is, there are two positive constants c and C so that for p(n) = cn−1/a(H) almost surely G(n, p(n)) does not have an H-factor, whereas for p(n) = Cn−1/a(H), almost surely G(n, p(n)) contains an H-factor (provided h divides n). A special case of this answers a problem of Erdős.

