Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T20:15:37.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Testing Expansion in Bounded-Degree Graphs

Published online by Cambridge University Press:  09 June 2010

ARTUR CZUMAJ  and
CHRISTIAN SOHLER
ARTUR CZUMAJ
Affiliation:
Department of Computer Science and Centre for Discrete Mathematics and its Applications (DIMAP), University of Warwick, Coventry CV4 7AL, UK (e-mail: [email protected])
CHRISTIAN SOHLER
Affiliation:
Department of Computer Science, Technische Universität Dortmund, D-44221 Dortmund, Germany (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

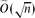We consider the problem of testing expansion in bounded-degree graphs. We focus on the notion of vertex expansion: an α-expander is a graph G = (V, E) in which every subset U ⊆ V of at most |V|/2 vertices has a neighbourhood of size at least α ⋅ |U|. Our main result is that one can distinguish good expanders from graphs that are far from being weak expanders in time . We prove that the property-testing algorithm proposed by Goldreich and Ron with appropriately set parameters accepts every α-expander with probability at least and rejects every graph that is ϵ-far from any α*-expander with probability at least , where 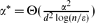and d is the maximum degree of the graphs. The algorithm assumes the bounded-degree graphs model with adjacency list graph representation and its running time is .

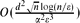Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 693 - 709
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. (1986) Eigenvalues and expanders. Combinatorica 6 83–96.CrossRefGoogle Scholar
[2]Alon, N., Fischer, E., Newman, I. and Shapira, A. (2009) A combinatorial characterization of the testable graph properties: It's all about regularity. SIAM J. Comput. 39 143–167.CrossRefGoogle Scholar
[3]Alon, N. and Milman, V. D. (1985) λ1, isoperimetric inequalities for graphs, and superconcentrators. J. Combin. Theory Ser. B 38 73–88.CrossRefGoogle Scholar
[4]Alon, N. and Shapira, A. (2008) A characterization of the (natural) graph properties testable with one-sided error. SIAM J. Comput. 37 1703–1727.CrossRefGoogle Scholar
[5]Batu, T., Fortnow, L., Rubinfeld, R., Smith, W. and White, P. (2000) Testing that distributions are close. In Proc. 41st IEEE Symposium on Foundations of Computer Science (FOCS), pp. 259–269.CrossRefGoogle Scholar
[6]Bender, M. A. and Ron, D. (2002) Testing properties of directed graphs: Acyclicity and connectivity. Random Struct. Alg. 20 184–205.CrossRefGoogle Scholar
[7]Benjamini, I., Schramm, O. and Shapira, A. (2008) Every minor-closed property of sparse graphs is testable. In Proc. 40th Annual ACM Symposium on Theory of Computing (STOC), pp. 393–402.CrossRefGoogle Scholar
[8]Bogdanov, A., Obata, K. and Trevisan, L. (2002) A lower bound for testing 3-colorability in bounded-degree graphs. In Proc. 43rd IEEE Symposium on Foundations of Computer Science (FOCS), pp. 93–102.CrossRefGoogle Scholar
[9]Borgs, C., Chayes, J., Lovász, L., Sos, V. T., Szegedy, B. and Vesztergombi, K. (2006) Graph limits and parameter testing. In Proc. 38th Annual ACM Symposium on Theory of Computing (STOC), 261–270.CrossRefGoogle Scholar
[10]Czumaj, A., Shapira, A. and Sohler, C. (2009) Testing hereditary properties of non-expanding bounded-degree graphs. SIAM J. Comput. 38 2499–2510.CrossRefGoogle Scholar
[11]Czumaj, A. and Sohler, C. (2005) Abstract combinatorial programs and efficient property testers. SIAM J. Comput. 34 580–615.CrossRefGoogle Scholar
[12]Czumaj, A. and Sohler, C. (2006) Sublinear-time algorithms. Bull. EATCS 89 23–47.Google Scholar
[13]Fischer, E. (2001) The art of uninformed decisions: A primer to property testing. Bull. EATCS 75 97–126.Google Scholar
[14]Friedman, J. (2004) A proof of Alon's second eigenvalue conjecture. Mem. Amer. Math. Soc., to appear.CrossRefGoogle Scholar
[15]Goldreich, O. and Ron, D. (1999) A sublinear bipartiteness tester for bounded degree graphs. Combinatorica 19 335–373.CrossRefGoogle Scholar
[16]Goldreich, O. and Ron, D. (2000) On testing expansion in bounded-degree graphs. Electronic Colloquium on Computational Complexity (ECCC), Report no. 7.Google Scholar
[17]Goldreich, O. and Ron, D. (2002) Property testing in bounded degree graphs. Algorithmica 32 302–343.CrossRefGoogle Scholar
[18]Hoory, S., Linial, N. and Wigderson, A. (2006) Expander graphs and their applications. Bull. Amer. Math. Soc. 43 439–561.CrossRefGoogle Scholar
[19]Kale, S. and Seshadhri, C. (2007) Testing expansion in bounded degree graphs. Electronic Colloquium on Computational Complexity (ECCC) TR-07-076.Google Scholar
[20]Kale, S. and Seshadhri, C. (2008) An expansion tester for bounded degree graphs. Proc 35th Annual International Colloquium on Automata, Languages and Programming (ICALP), pp. 527–538.CrossRefGoogle Scholar
[21]Kumar, R. and Rubinfeld, R. (2003) Sublinear time algorithms. SIGACT News 34 57–67.CrossRefGoogle Scholar
[22]Jerrum, M. and Sinclair, A. (1996) The Markov chain Monte Carlo method: An approach to approximate counting and integration. Chapter 12 in Approximation Algorithms for NP-hard Problems (Hochbaum, D., ed.), PWS Publishing, Boston.Google Scholar
[23]Nachmias, A. and Shapira, A. (2007) Testing the expansion of a graph. Electronic Colloquium on Computational Complexity (ECCC) TR-07-118.Google Scholar
[24]Parnas, M. and Ron, D. (2002) Testing the diameter of graphs. Random Struct. Alg. 20 165–183.CrossRefGoogle Scholar
[25]Ron, D. (2001) Property testing. In Handbook of Randomized Algorithms (Pardalos, P. M., Rajasekaran, S., Reif, J., and Rolim, J. D. P., eds), Vol. II, Kluwer, pp. 597–649.CrossRefGoogle Scholar
[26]Sinclair, A. (1992) Improved bounds for mixing rates of Markov chains and multicommodity flow. Combin. Probab. Comput. 1 351–370.CrossRefGoogle Scholar
[27]Sinclair, A. and Jerrum, M. (1989) Approximate counting, uniform generation and rapidly mixing Markov chains. Inform. Comput. 82 93–133.CrossRefGoogle Scholar