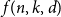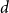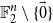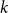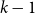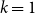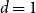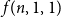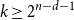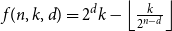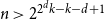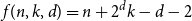1. Introduction
How many affine hyperplanes does it take to cover the vertices of the
![]() $n$
-dimensional Boolean hypercube,
$n$
-dimensional Boolean hypercube,
![]() $\{0,1\}^n$
? This simple question has an equally straightforward answer—one can cover all the vertices with a parallel pair of hyperplanes, while it is easy to see that a single plane can cover at most half the vertices, and so two planes are indeed necessary. However, the waters are quickly muddied with a minor twist to the problem.
$\{0,1\}^n$
? This simple question has an equally straightforward answer—one can cover all the vertices with a parallel pair of hyperplanes, while it is easy to see that a single plane can cover at most half the vertices, and so two planes are indeed necessary. However, the waters are quickly muddied with a minor twist to the problem.
Indeed, if one is instead asked to cover all the vertices except the origin, the parallel hyperplane construction is no longer valid. Given a moment’s thought, one might come up with the much larger family of
![]() $n$
hyperplanes given by
$n$
hyperplanes given by
![]() $\{ \vec{x} \;:\; x_i = 1 \}$
for
$\{ \vec{x} \;:\; x_i = 1 \}$
for
![]() $i \in [n]$
. This fulfils the task and, surprisingly, turns out to be optimal [Reference Alon and Füredi1], although this is far from obvious. This problem has led to rich veins of research in both finite geometry and extremal combinatorics, and in what follows we survey its history before introducing our new results.
$i \in [n]$
. This fulfils the task and, surprisingly, turns out to be optimal [Reference Alon and Füredi1], although this is far from obvious. This problem has led to rich veins of research in both finite geometry and extremal combinatorics, and in what follows we survey its history before introducing our new results.
1.1. An origin story
When we work over the finite field
![]() $\mathbb{F}_{2}^{}$
, this problem is equivalent to the well-known blocking set problem from finite geometry, and it was in this guise that it was first studied. A blocking set in
$\mathbb{F}_{2}^{}$
, this problem is equivalent to the well-known blocking set problem from finite geometry, and it was in this guise that it was first studied. A blocking set in
![]() $\mathbb{F}_{2}^{n}$
is a set of points that meets every hyperplane, and the objective is to find a blocking set of minimum size. By translating, we may assume that our blocking set contains the origin
$\mathbb{F}_{2}^{n}$
is a set of points that meets every hyperplane, and the objective is to find a blocking set of minimum size. By translating, we may assume that our blocking set contains the origin
![]() $\vec{0}$
, and so the problem reduces to finding a collection of points that meets all hyperplanes avoiding the origin. Applying duality, we return to our original problem of covering the nonzero points of
$\vec{0}$
, and so the problem reduces to finding a collection of points that meets all hyperplanes avoiding the origin. Applying duality, we return to our original problem of covering the nonzero points of
![]() $\mathbb{F}_{2}^{n}$
with affine hyperplanes.
$\mathbb{F}_{2}^{n}$
with affine hyperplanes.
There is no reason to restrict our attention to the binary field
![]() $\mathbb{F}_{2}^{}$
, and we can generalise the problem to ask how many hyperplanes are needed to cover the nonzero points of
$\mathbb{F}_{2}^{}$
, and we can generalise the problem to ask how many hyperplanes are needed to cover the nonzero points of
![]() $\mathbb{F}_{q}^{n}$
. Going even further, one may replace the hyperplanes with affine subspaces of codimension
$\mathbb{F}_{q}^{n}$
. Going even further, one may replace the hyperplanes with affine subspaces of codimension
![]() $d$
. In this generality, the problem was answered in the late 1970s by Jamison [Reference Jamison16], who proved that the minimum number of affine subspaces of codimension
$d$
. In this generality, the problem was answered in the late 1970s by Jamison [Reference Jamison16], who proved that the minimum number of affine subspaces of codimension
![]() $d$
that cover all nonzero points in
$d$
that cover all nonzero points in
![]() $\mathbb{F}_{q}^{n}$
while avoiding the origin is
$\mathbb{F}_{q}^{n}$
while avoiding the origin is
![]() $q^d - 1 + (n-d)(q-1)$
. In particular, when
$q^d - 1 + (n-d)(q-1)$
. In particular, when
![]() $q = 2$
and
$q = 2$
and
![]() $d=1$
, this lower bound is equal to
$d=1$
, this lower bound is equal to
![]() $n$
, showing that the earlier construction with
$n$
, showing that the earlier construction with
![]() $n$
planes is optimal. A simpler proof of the case
$n$
planes is optimal. A simpler proof of the case
![]() $d=1$
was independently provided by Brouwer and Schrijver [Reference Brouwer and Schrijver7].
$d=1$
was independently provided by Brouwer and Schrijver [Reference Brouwer and Schrijver7].
While the finite geometry motivation naturally leads one to work over finite fields, one can also study the problem over infinite fields
![]() $\mathbb{F}_{}^{}$
. Of course, one would need infinitely many hyperplanes to cover all nonzero points of
$\mathbb{F}_{}^{}$
. Of course, one would need infinitely many hyperplanes to cover all nonzero points of
![]() $\mathbb{F}_{}^{n}$
, which is why we instead ask how many hyperplanes are needed to cover the nonzero points of the hypercube
$\mathbb{F}_{}^{n}$
, which is why we instead ask how many hyperplanes are needed to cover the nonzero points of the hypercube
![]() $\{0,1\}^n \subseteq{\mathbb{F}_{}^{n}}$
. This problem was raised in the early 1990s by Komjáth [Reference Komjáth18], who, in order to prove some results in infinite Ramsey theory, showed that this quantity must grow with
$\{0,1\}^n \subseteq{\mathbb{F}_{}^{n}}$
. This problem was raised in the early 1990s by Komjáth [Reference Komjáth18], who, in order to prove some results in infinite Ramsey theory, showed that this quantity must grow with
![]() $n$
. Shortly afterwards, a celebrated result of Alon and Füredi [Reference Alon and Füredi1] established a tight bound in the more general setting of covering all but one point of a finite grid. They showed that, for any collection of finite subsets
$n$
. Shortly afterwards, a celebrated result of Alon and Füredi [Reference Alon and Füredi1] established a tight bound in the more general setting of covering all but one point of a finite grid. They showed that, for any collection of finite subsets
![]() $S_1, S_2, \ldots, S_n$
of some arbitrary field
$S_1, S_2, \ldots, S_n$
of some arbitrary field
![]() $\mathbb{F}_{}^{}$
, the minimum number of hyperplanes needed to cover all but one point of
$\mathbb{F}_{}^{}$
, the minimum number of hyperplanes needed to cover all but one point of
![]() $S_1 \times S_2 \times \ldots \times S_n$
is
$S_1 \times S_2 \times \ldots \times S_n$
is
![]() $\sum _i ( |{S_i}| - 1 )$
. If we take
$\sum _i ( |{S_i}| - 1 )$
. If we take
![]() $S_i = \{0,1\}$
for all
$S_i = \{0,1\}$
for all
![]() $i$
, this once again shows that one needs
$i$
, this once again shows that one needs
![]() $n$
hyperplanes to cover the nonzero points of the hypercube.
$n$
hyperplanes to cover the nonzero points of the hypercube.
1.2. The polynomial method
Despite these motivating applications to finite geometry and Ramsey theory, the primary reason this problem has attracted so much attention lies in the proof methods used. These hyperplane covers have driven the development of the polynomial method—indeed, in light of his early results, this is sometimes referred to as the Jamison method in finite geometry [Reference Bruen and Fisher9].
To see how polynomials come into play, suppose we have a set of hyperplanes
![]() $\{H_i \;:\; i \in [m] \}$
in
$\{H_i \;:\; i \in [m] \}$
in
![]() $\mathbb{F}_{}^{n}$
, with the plane
$\mathbb{F}_{}^{n}$
, with the plane
![]() $H_i$
defined by
$H_i$
defined by
![]() $H_i = \{ \vec{x} \;:\; \vec{x} \cdot \vec{a}_i = c_i \}$
for some normal vector
$H_i = \{ \vec{x} \;:\; \vec{x} \cdot \vec{a}_i = c_i \}$
for some normal vector
![]() $\vec{a}_i \in{\mathbb{F}_{}^{n}}$
and some constant
$\vec{a}_i \in{\mathbb{F}_{}^{n}}$
and some constant
![]() $c_i \in{\mathbb{F}_{}^{}}$
. We can then define the degree-
$c_i \in{\mathbb{F}_{}^{}}$
. We can then define the degree-
![]() $m$
polynomial
$m$
polynomial
![]() $f(\vec{x}) = \prod _{i \in m} ( \vec{x} \cdot \vec{a}_i - c_i )$
, observing that
$f(\vec{x}) = \prod _{i \in m} ( \vec{x} \cdot \vec{a}_i - c_i )$
, observing that
![]() $f(\vec{x}) = 0$
if and only if
$f(\vec{x}) = 0$
if and only if
![]() $\vec{x}$
is covered by one of the hyperplanes
$\vec{x}$
is covered by one of the hyperplanes
![]() $H_i$
. Thus, lower bounds on the degrees of polynomials that vanish except at the origin translate to lower bounds on the number of hyperplanes needed to cover all nonzero points.
$H_i$
. Thus, lower bounds on the degrees of polynomials that vanish except at the origin translate to lower bounds on the number of hyperplanes needed to cover all nonzero points.
This approach has proven very robust, and lends itself to a number of generalisations. For instance, Kós, Mészáros and Rónyai [Reference Kós, Mészáros and Rónyai20] and Bishnoi, Clark, Potukuchi and Schmitt [Reference Bishnoi, Clark, Potukuchi and Schmitt5] considered variations over rings, while Blokhuis, Brouwer and Szőnyi [Reference Blokhuis, Brouwer and Szőnyi6] studied the problem for quadratic surfaces and Hermitian varieties in projective and affine spaces over
![]() $\mathbb{F}_{q}^{}$
.
$\mathbb{F}_{q}^{}$
.
1.3. Covering with multiplicity
In this paper, we shall remain in the original setting, but instead extend the problem to higher multiplicities. That is, we shall seek the minimum number of hyperplanes in
![]() $\mathbb{F}_{}^{n}$
needed to cover the nonzero points at least
$\mathbb{F}_{}^{n}$
needed to cover the nonzero points at least
![]() $k$
times, while covering the origin fewer times. Previous work in this direction has imposed the stricter condition of avoiding the origin altogether; Bruen [Reference Bruen8] considered this problem over finite fields, while Ball and Serra [Reference Ball and Serra4] and Kós and Rónyai [Reference Kós and Rónyai19] worked with finite grids over arbitrary fields, with some further generalisations recently provided by Geil and Matrínez-Penas [Reference Geil and Matrínez-Peñas12]. In all of these papers, the polynomial method described above was strengthened to obtain lower bounds for this problem with higher multiplicities. However, these lower bounds are most often not tight; Zanella [Reference Zanella26] discusses when Bruen’s bound is sharp, with some improvements provided by Ball [Reference Ball2].
$k$
times, while covering the origin fewer times. Previous work in this direction has imposed the stricter condition of avoiding the origin altogether; Bruen [Reference Bruen8] considered this problem over finite fields, while Ball and Serra [Reference Ball and Serra4] and Kós and Rónyai [Reference Kós and Rónyai19] worked with finite grids over arbitrary fields, with some further generalisations recently provided by Geil and Matrínez-Penas [Reference Geil and Matrínez-Peñas12]. In all of these papers, the polynomial method described above was strengthened to obtain lower bounds for this problem with higher multiplicities. However, these lower bounds are most often not tight; Zanella [Reference Zanella26] discusses when Bruen’s bound is sharp, with some improvements provided by Ball [Reference Ball2].
Significant progress in this line of research was made recently when Clifton and Huang [Reference Clifton and Huang10] studied the special case of covering all nonzero points of
![]() $\{0,1\}^n \subseteq \mathbb{R}^n$
at least
$\{0,1\}^n \subseteq \mathbb{R}^n$
at least
![]() $k$
times, while leaving the origin uncovered. Observe that one can remove
$k$
times, while leaving the origin uncovered. Observe that one can remove
![]() $k-1$
hyperplanes arbitrarily from such a cover, and the remainder will still cover each nonzero point at least once. Thus, by the Alon–Füredi theorem, we must be left with at least
$k-1$
hyperplanes arbitrarily from such a cover, and the remainder will still cover each nonzero point at least once. Thus, by the Alon–Füredi theorem, we must be left with at least
![]() $n$
planes, giving a lower bound of
$n$
planes, giving a lower bound of
![]() $n+k-1$
. While it is not hard to see that this is tight for
$n+k-1$
. While it is not hard to see that this is tight for
![]() $k=2$
, Clifton and Huang used Ball and Serra’s Punctured Combinatorial Nullstellensatz [Reference Ball and Serra4] to improve the lower bound for larger
$k=2$
, Clifton and Huang used Ball and Serra’s Punctured Combinatorial Nullstellensatz [Reference Ball and Serra4] to improve the lower bound for larger
![]() $k$
. They showed that for
$k$
. They showed that for
![]() $k = 3$
and
$k = 3$
and
![]() $n \ge 2$
, the correct answer is
$n \ge 2$
, the correct answer is
![]() $n + 3$
, while for
$n + 3$
, while for
![]() $k \ge 4$
and
$k \ge 4$
and
![]() $n \ge 3$
, the answer lies between
$n \ge 3$
, the answer lies between
![]() $n + k + 1$
and
$n + k + 1$
and
![]() $n + \binom{k}{2}$
; additionally, they conjectured the upper bound to be correct when
$n + \binom{k}{2}$
; additionally, they conjectured the upper bound to be correct when
![]() $n$
is large with respect to
$n$
is large with respect to
![]() $k$
. However, they showed that this was far from the case when
$k$
. However, they showed that this was far from the case when
![]() $n$
is fixed and
$n$
is fixed and
![]() $k$
is large; in this range, the answer is
$k$
is large; in this range, the answer is
![]() $(c_n + o(1))k$
, where
$(c_n + o(1))k$
, where
![]() $c_n$
is the
$c_n$
is the
![]() $n$
th term in the harmonic series.
$n$
th term in the harmonic series.
A major breakthrough was then made by Sauermann and Wigderson [Reference Sauermann and Wigderson24], who skipped the geometric motivation and resolved the polynomial problem directly. More precisely, they proved the following theorem.
Theorem 1.1.
Let
![]() $k \ge 2$
and
$k \ge 2$
and
![]() $n \ge 2k-3$
, and let
$n \ge 2k-3$
, and let
![]() $P \in \mathbb{R}[x_1, \ldots, x_n]$
be a polynomial having zeroes of multiplicity at least
$P \in \mathbb{R}[x_1, \ldots, x_n]$
be a polynomial having zeroes of multiplicity at least
![]() $k$
at all points in
$k$
at all points in
![]() $\{0,1\}^n \setminus \{ \vec{0} \}$
, and such that
$\{0,1\}^n \setminus \{ \vec{0} \}$
, and such that
![]() $P$
does not have a zero of multiplicity at least
$P$
does not have a zero of multiplicity at least
![]() $k-1$
at
$k-1$
at
![]() $\vec{0}$
. Then
$\vec{0}$
. Then
![]() $P$
must have degree at least
$P$
must have degree at least
![]() $n + 2k - 3$
. Furthermore, for every
$n + 2k - 3$
. Furthermore, for every
![]() $\ell \in \{0, 1, \ldots, k-2\}$
, there exists a polynomial
$\ell \in \{0, 1, \ldots, k-2\}$
, there exists a polynomial
![]() $P$
with degree exactly
$P$
with degree exactly
![]() $n + 2k - 3$
having zeroes of multiplicity at least
$n + 2k - 3$
having zeroes of multiplicity at least
![]() $k$
at all points in
$k$
at all points in
![]() $\{0,1\}^n \setminus \{ \vec{0} \}$
, and such that
$\{0,1\}^n \setminus \{ \vec{0} \}$
, and such that
![]() $P$
has a zero of multiplicity exactly
$P$
has a zero of multiplicity exactly
![]() $\ell$
at
$\ell$
at
![]() $\vec{0}$
.
$\vec{0}$
.
As an immediate corollary, this improves the lower bound in the Clifton–Huang result from
![]() $n+k+1$
to
$n+k+1$
to
![]() $n+2k-3$
. However, Theorem 1.1 establishes that
$n+2k-3$
. However, Theorem 1.1 establishes that
![]() $n+2k-3$
is also an upper bound for the polynomial problem, whereas Clifton and Huang conjecture that the answer for their problem should be
$n+2k-3$
is also an upper bound for the polynomial problem, whereas Clifton and Huang conjecture that the answer for their problem should be
![]() $n + \binom{k}{2}$
. An affirmative answer to this conjecture would thus demonstrate separation between the algebraic polynomial problem and the geometric covering problem.
$n + \binom{k}{2}$
. An affirmative answer to this conjecture would thus demonstrate separation between the algebraic polynomial problem and the geometric covering problem.
Even though Theorem 1.1 is stated for polynomials defined over
![]() $\mathbb{R}$
, Sauermann and Wigderson note that the proof works over any field of characteristic zero. However, the result need not hold over finite fields. In particular, they show the existence of a polynomial
$\mathbb{R}$
, Sauermann and Wigderson note that the proof works over any field of characteristic zero. However, the result need not hold over finite fields. In particular, they show the existence of a polynomial
![]() $P_4$
over
$P_4$
over
![]() $\mathbb{F}_{2}^{}$
of degree
$\mathbb{F}_{2}^{}$
of degree
![]() $n + 4$
with zeroes of multiplicity four at all nonzero points in
$n + 4$
with zeroes of multiplicity four at all nonzero points in
![]() $\mathbb{F}_{2}^{n}$
and with
$\mathbb{F}_{2}^{n}$
and with
![]() $P_4(\vec{0}) \neq 0$
. More generally, for every
$P_4(\vec{0}) \neq 0$
. More generally, for every
![]() $k \ge 4$
,
$k \ge 4$
,
![]() $P_k(\vec{x}) = x_1^{k-4} (x_1 - 1)^{k-4} P_4(\vec{x})$
is a binary polynomial of degree only
$P_k(\vec{x}) = x_1^{k-4} (x_1 - 1)^{k-4} P_4(\vec{x})$
is a binary polynomial of degree only
![]() $n + 2k - 4$
with zeroes of multiplicity
$n + 2k - 4$
with zeroes of multiplicity
![]() $k$
at all nonzero points and of multiplicity
$k$
at all nonzero points and of multiplicity
![]() $k-4$
at the origin. The correct behaviour of the problem over finite fields is left as an open problem.
$k-4$
at the origin. The correct behaviour of the problem over finite fields is left as an open problem.
Note also that Theorem 1.1 allows the origin to be covered up to
![]() $k-2$
times. Sauermann and Wigderson also considered the case where the origin must be covered with multiplicity exactly
$k-2$
times. Sauermann and Wigderson also considered the case where the origin must be covered with multiplicity exactly
![]() $k-1$
, showing that the minimum degree then increases to
$k-1$
, showing that the minimum degree then increases to
![]() $n+2k-2$
. In contrast to Theorem 1.1, the proof of this result is valid over all fields.
$n+2k-2$
. In contrast to Theorem 1.1, the proof of this result is valid over all fields.
1.4. Our results
In this paper, we study the problem of covering with multiplicity in
![]() $\mathbb{F}_{2}^{n}$
. We are motivated not only by the body of research described above, but also by the fact that, as we shall show in Proposition 3.3, when one forbids the origin from being covered, this problem is equivalent to finding linear binary codes of large minimum distance. As this classic problem from coding theory has a long and storied history of its own, and is likely to be very difficult, we shall instead work in the setting where we require all nonzero points in
$\mathbb{F}_{2}^{n}$
. We are motivated not only by the body of research described above, but also by the fact that, as we shall show in Proposition 3.3, when one forbids the origin from being covered, this problem is equivalent to finding linear binary codes of large minimum distance. As this classic problem from coding theory has a long and storied history of its own, and is likely to be very difficult, we shall instead work in the setting where we require all nonzero points in
![]() $\mathbb{F}_{2}^{n}$
to be covered at least
$\mathbb{F}_{2}^{n}$
to be covered at least
![]() $k$
times while the origin can be covered at most
$k$
times while the origin can be covered at most
![]() $k-1$
times.
$k-1$
times.
In light of the previous results, we shall abstain from employing the polynomial method, and instead attack the problem more directly with combinatorial techniques. As an added bonus, our arguments readily generalise to covering points with codimension-
![]() $d$
affine subspaces, rather than just hyperplanes, thereby extending Jamison’s original results in the case
$d$
affine subspaces, rather than just hyperplanes, thereby extending Jamison’s original results in the case
![]() $q=2$
. To be able to discuss our results more concisely, we first introduce some notation that we will use throughout the paper.
$q=2$
. To be able to discuss our results more concisely, we first introduce some notation that we will use throughout the paper.
Given integers
![]() $k \ge 1$
and
$k \ge 1$
and
![]() $n \ge d \ge 1$
, we say a multiset
$n \ge d \ge 1$
, we say a multiset
![]() $\mathcal{H}$
of
$\mathcal{H}$
of
![]() $(n-d)$
-dimensional affine subspaces in
$(n-d)$
-dimensional affine subspaces in
![]() $\mathbb{F}_{2}^{n}$
is a
$\mathbb{F}_{2}^{n}$
is a
![]() $(k,d)$
-cover if every nonzero point of
$(k,d)$
-cover if every nonzero point of
![]() $\mathbb{F}_{2}^{n}$
is covered at least
$\mathbb{F}_{2}^{n}$
is covered at least
![]() $k$
times, while
$k$
times, while
![]() $\vec{0}$
is covered at most
$\vec{0}$
is covered at most
![]() $k-1$
times. We then define the corresponding extremal function
$k-1$
times. We then define the corresponding extremal function
![]() $f(n,k,d)$
to be the minimum possible size of a
$f(n,k,d)$
to be the minimum possible size of a
![]() $(k,d)$
-cover in
$(k,d)$
-cover in
![]() $\mathbb{F}_{2}^{n}$
.
$\mathbb{F}_{2}^{n}$
.
For instance, when we take
![]() $k = 1$
, we obtain the original covering problem, and from the work of Jamison [Reference Jamison16] we know
$k = 1$
, we obtain the original covering problem, and from the work of Jamison [Reference Jamison16] we know
![]() $f(n,1,d) = n + 2^d - d - 1$
. At another extreme, if we take
$f(n,1,d) = n + 2^d - d - 1$
. At another extreme, if we take
![]() $d = n$
, then our affine subspaces are simply individual points, each of which must be covered
$d = n$
, then our affine subspaces are simply individual points, each of which must be covered
![]() $k$
times, and hence
$k$
times, and hence
![]() $f(n,k,n) = k ( 2^n - 1 )$
. We study this function for intermediate values of the parameters, determining it precisely when either
$f(n,k,n) = k ( 2^n - 1 )$
. We study this function for intermediate values of the parameters, determining it precisely when either
![]() $k$
is large with respect to
$k$
is large with respect to
![]() $n$
and
$n$
and
![]() $d$
, or
$d$
, or
![]() $n$
is large with respect to
$n$
is large with respect to
![]() $k$
and
$k$
and
![]() $d$
, and deriving asymptotic results otherwise.
$d$
, and deriving asymptotic results otherwise.
Theorem 1.2.
Let
![]() $k \ge 1$
and
$k \ge 1$
and
![]() $n \ge d \ge 1$
. Then:
$n \ge d \ge 1$
. Then:
-
(a) If
 $k \ge 2^{n-d-1}$
, then
$k \ge 2^{n-d-1}$
, then
 $f(n,k,d) = 2^d k - \left \lfloor{ \frac{k}{2^{n-d}} }\right\rfloor$
.
$f(n,k,d) = 2^d k - \left \lfloor{ \frac{k}{2^{n-d}} }\right\rfloor$
. -
(b) If
 $k\geq 2$
and
$k\geq 2$
and
 $n \gt 2^{2^d k - d - k + 1}$
, then
$n \gt 2^{2^d k - d - k + 1}$
, then
 $f(n,k,d) = n + 2^d k - d - 2$
.
$f(n,k,d) = n + 2^d k - d - 2$
. -
(c) If
 $k \ge 2$
and
$k \ge 2$
and
 $n \ge \lfloor{\log _2 k}\rfloor + d + 1$
, then
$n \ge \lfloor{\log _2 k}\rfloor + d + 1$
, then
 $n + 2^d k - d - \log _2\!(2k) \le f(n,k,d) \le n + 2^d k - d - 2$
.
$n + 2^d k - d - \log _2\!(2k) \le f(n,k,d) \le n + 2^d k - d - 2$
.
There are a few remarks worth making at this stage. First, observe that, just as in the Clifton–Huang setting, the extremal function
![]() $f(n,k,d)$
exhibits different behaviour when
$f(n,k,d)$
exhibits different behaviour when
![]() $n$
is fixed and
$n$
is fixed and
![]() $k$
is large as compared to when
$k$
is large as compared to when
![]() $k$
is fixed and
$k$
is fixed and
![]() $n$
is large. Second, and perhaps most significantly, Theorem 1.2 demonstrates the gap between the hyperplane covering problem and the polynomial degree problem: our result shows that, for any
$n$
is large. Second, and perhaps most significantly, Theorem 1.2 demonstrates the gap between the hyperplane covering problem and the polynomial degree problem: our result shows that, for any
![]() $k\geq 4$
and sufficiently large
$k\geq 4$
and sufficiently large
![]() $n$
, we have
$n$
, we have
![]() $f(n,k,1) = n + 2k - 3$
, whereas the answer to the corresponding polynomial problem is at most
$f(n,k,1) = n + 2k - 3$
, whereas the answer to the corresponding polynomial problem is at most
![]() $n + 2k - 4$
, as explained after Theorem 1.1. Our ideas allow us to establish an even stronger separation in the case
$n + 2k - 4$
, as explained after Theorem 1.1. Our ideas allow us to establish an even stronger separation in the case
![]() $k = 4$
—while the polynomial
$k = 4$
—while the polynomial
![]() $P_4$
constructed by Sauermann and Wigderson, which has zeroes of multiplicity at least four at all nonzero points of
$P_4$
constructed by Sauermann and Wigderson, which has zeroes of multiplicity at least four at all nonzero points of
![]() $\mathbb{F}_{2}^{n}$
while not vanishing at the origin, has degree only
$\mathbb{F}_{2}^{n}$
while not vanishing at the origin, has degree only
![]() $n + 4$
, we shall show in Corollary 3.5 that any hyperplane system with the corresponding covering properties must have size at least
$n + 4$
, we shall show in Corollary 3.5 that any hyperplane system with the corresponding covering properties must have size at least
![]() $n + \log _2 \left ( \tfrac 23 n \right )$
. Third, we see that in the intermediate range, when both
$n + \log _2 \left ( \tfrac 23 n \right )$
. Third, we see that in the intermediate range, when both
![]() $n$
and
$n$
and
![]() $k$
grow moderately, the bounds in (c) determine
$k$
grow moderately, the bounds in (c) determine
![]() $f(n,k,d)$
up to an additive error of
$f(n,k,d)$
up to an additive error of
![]() $\log _2\!(2k)$
, which is a lower-order term. Thus,
$\log _2\!(2k)$
, which is a lower-order term. Thus,
![]() $f(n,k,d)$
grows asymptotically like
$f(n,k,d)$
grows asymptotically like
![]() $n + 2^d k$
. Last of all, if one substitutes
$n + 2^d k$
. Last of all, if one substitutes
![]() $k = 2^{n-d-1} - 1$
, the lower bound from (c) is larger than the value in (a). This shows that
$k = 2^{n-d-1} - 1$
, the lower bound from (c) is larger than the value in (a). This shows that
![]() $k \ge 2^{n-d-1}$
is indeed the correct range for which the result in (a) is valid. In contrast, we believe the bound on
$k \ge 2^{n-d-1}$
is indeed the correct range for which the result in (a) is valid. In contrast, we believe the bound on
![]() $n$
in (b) is far from optimal, and discuss this in greater depth in the concluding remarks.
$n$
in (b) is far from optimal, and discuss this in greater depth in the concluding remarks.
The remainder of this paper is devoted to the proof of Theorem 1.2, and is organised as follows. In Section 2 we prove part (a), determining the extremal function for large multiplicities. We prove part (b) in Section 3, handling the case when the dimension of the ambient space grows quickly. A key step in the proof is showing the intuitive, yet surprisingly not immediate, fact that
![]() $f(n,k,d)$
is strictly increasing in
$f(n,k,d)$
is strictly increasing in
![]() $n$
, as a result of which we shall also be able to deduce the bounds in (c). We end by presenting some concluding remarks and open problems in Section 4.
$n$
, as a result of which we shall also be able to deduce the bounds in (c). We end by presenting some concluding remarks and open problems in Section 4.
2. Covering with large multiplicity
In this section we prove Theorem 1.2(a), handling the case of large multiplicities. We begin by introducing some definitions and notation that we will use in the proof. To start with, it will be convenient to have some notation for affine hyperplanes. Given a nonzero vector
![]() $\vec{u}\in{\mathbb{F}_{2}^{n}}$
, let
$\vec{u}\in{\mathbb{F}_{2}^{n}}$
, let
![]() $H_{\vec{u}}$
denote the hyperplane
$H_{\vec{u}}$
denote the hyperplane
![]() $\{ \vec{x} \;:\; \vec{x} \cdot \vec{u} = 1 \}$
.
$\{ \vec{x} \;:\; \vec{x} \cdot \vec{u} = 1 \}$
.
Next, it will sometimes be helpful to specify how many times the origin is covered. Hence, given integers
![]() $n \ge d \ge 1$
and
$n \ge d \ge 1$
and
![]() $k \gt s \ge 0$
, we call a
$k \gt s \ge 0$
, we call a
![]() $(k,d)$
-cover in
$(k,d)$
-cover in
![]() $\mathbb{F}_{2}^{n}$
a
$\mathbb{F}_{2}^{n}$
a
![]() $(k,d;\;s)$
-cover if it covers the origin exactly
$(k,d;\;s)$
-cover if it covers the origin exactly
![]() $s$
times. Let us write
$s$
times. Let us write
![]() $g(n,k,d;\;s)$
for the minimum possible size of a
$g(n,k,d;\;s)$
for the minimum possible size of a
![]() $(k,d;\;s)$
-cover in
$(k,d;\;s)$
-cover in
![]() $\mathbb{F}_{2}^{n}$
and call a cover optimal if it has this minimum size. Clearly, we have
$\mathbb{F}_{2}^{n}$
and call a cover optimal if it has this minimum size. Clearly, we have
![]() $f(n,k,d)=\min _{0\leq s\lt k} g(n,k,d;\;s)$
, so any knowledge about this more refined function directly translates to our main focus of interest.
$f(n,k,d)=\min _{0\leq s\lt k} g(n,k,d;\;s)$
, so any knowledge about this more refined function directly translates to our main focus of interest.
2.1. The lower bound
To start with, we prove a general lower bound, valid for all choices of parameters, that follows from a simple double-counting argument. This establishes the lower bound of Theorem 1.2(a).
Lemma 2.1.
Let
![]() $n,k,d,s$
be integers such that
$n,k,d,s$
be integers such that
![]() $n \ge d \ge 1$
and
$n \ge d \ge 1$
and
![]() $k \gt s \ge 0$
. Then
$k \gt s \ge 0$
. Then
In particular,
![]() $f(n,k,d) \ge 2^d k - \left\lfloor{\frac{k}{2^{n-d}}}\right\rfloor$
.
$f(n,k,d) \ge 2^d k - \left\lfloor{\frac{k}{2^{n-d}}}\right\rfloor$
.
Proof. Let
![]() $\mathcal{H}$
be an optimal
$\mathcal{H}$
be an optimal
![]() $(k,d;\;s)$
-cover of
$(k,d;\;s)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
, so that we have
$\mathbb{F}_{2}^{n}$
, so that we have
![]() $g(n,k,d;\;s) = |{\mathcal{H}}|$
. We double-count the pairs
$g(n,k,d;\;s) = |{\mathcal{H}}|$
. We double-count the pairs
![]() $(\vec{x}, S)$
with
$(\vec{x}, S)$
with
![]() $\vec{x} \in{\mathbb{F}_{2}^{n}}$
,
$\vec{x} \in{\mathbb{F}_{2}^{n}}$
,
![]() $S \in \mathcal{H}$
, and
$S \in \mathcal{H}$
, and
![]() $\vec{x} \in S$
. On the one hand, every affine subspace
$\vec{x} \in S$
. On the one hand, every affine subspace
![]() $S \in \mathcal{H}$
contains
$S \in \mathcal{H}$
contains
![]() $2^{n-d}$
points, and so there are
$2^{n-d}$
points, and so there are
![]() $2^{n-d} |{\mathcal{H}}|$
such pairs. On the other hand, since every nonzero point is covered at least
$2^{n-d} |{\mathcal{H}}|$
such pairs. On the other hand, since every nonzero point is covered at least
![]() $k$
times and the origin is covered
$k$
times and the origin is covered
![]() $s$
times, there are at least
$s$
times, there are at least
![]() $(2^n - 1)k+s$
such pairs. Thus
$(2^n - 1)k+s$
such pairs. Thus
![]() $(2^n - 1 )k + s \le 2^{n-d} |{\mathcal{H}}|$
, and the claimed lower bound follows from solving for
$(2^n - 1 )k + s \le 2^{n-d} |{\mathcal{H}}|$
, and the claimed lower bound follows from solving for
![]() $|{\mathcal{H}}|$
and observing that
$|{\mathcal{H}}|$
and observing that
![]() $g(n,k,d;\;s)$
is an integer. The bound on
$g(n,k,d;\;s)$
is an integer. The bound on
![]() $f(n,k,d)$
is obtained by noticing that our lower bound on
$f(n,k,d)$
is obtained by noticing that our lower bound on
![]() $g(n,k,d;\;s)$
is increasing in
$g(n,k,d;\;s)$
is increasing in
![]() $s$
, and is therefore minimised when
$s$
, and is therefore minimised when
![]() $s = 0$
.
$s = 0$
.
2.2. The upper bound construction
To prove the upper bound of Theorem 1.2(a), we must construct small
![]() $(k,d)$
-covers. As a first step, we introduce a recursive method for
$(k,d)$
-covers. As a first step, we introduce a recursive method for
![]() $(k,d;\;s)$
-covers that allows us to reduce to the
$(k,d;\;s)$
-covers that allows us to reduce to the
![]() $d = 1$
case.
$d = 1$
case.
Lemma 2.2.
For integers
![]() $n \ge d \ge 2$
and
$n \ge d \ge 2$
and
![]() $k \gt s \ge 0$
we have
$k \gt s \ge 0$
we have
and, therefore,
Proof. We first deduce the recursive bound on
![]() $g(n,k,d;\;s)$
. Let
$g(n,k,d;\;s)$
. Let
![]() $S_0 \subseteq{\mathbb{F}_{2}^{n}}$
be an arbitrary
$S_0 \subseteq{\mathbb{F}_{2}^{n}}$
be an arbitrary
![]() $(n - d + 1)$
-dimensional (vector) subspace, and let
$(n - d + 1)$
-dimensional (vector) subspace, and let
![]() $S_1, \ldots, S_{2^{d-1} - 1}$
be its affine translates, that, together with
$S_1, \ldots, S_{2^{d-1} - 1}$
be its affine translates, that, together with
![]() $S_0$
, partition
$S_0$
, partition
![]() $\mathbb{F}_{2}^{n}$
. For every
$\mathbb{F}_{2}^{n}$
. For every
![]() $1\leq i\leq 2^{d-1}-1$
, partition
$1\leq i\leq 2^{d-1}-1$
, partition
![]() $S_i \cong \mathbb{F}_2^{n - d+ 1}$
further into two subspaces, thereby obtaining a total of
$S_i \cong \mathbb{F}_2^{n - d+ 1}$
further into two subspaces, thereby obtaining a total of
![]() $2(2^{d - 1} - 1)$
affine subspaces of dimension
$2(2^{d - 1} - 1)$
affine subspaces of dimension
![]() $n - d$
. We start by taking
$n - d$
. We start by taking
![]() $k$
copies of each of these affine subspaces. This gives us a multiset of
$k$
copies of each of these affine subspaces. This gives us a multiset of
![]() $2k(2^{d - 1} - 1)$
subspaces, which cover every point outside
$2k(2^{d - 1} - 1)$
subspaces, which cover every point outside
![]() $S_0$
exactly
$S_0$
exactly
![]() $k$
times and leave the points in
$k$
times and leave the points in
![]() $S_0$
completely uncovered.
$S_0$
completely uncovered.
It thus remains to cover the points within
![]() $S_0$
appropriately. Since
$S_0$
appropriately. Since
![]() $(n-d)$
-dimensional subspaces have relative codimension
$(n-d)$
-dimensional subspaces have relative codimension
![]() $1$
in
$1$
in
![]() $S_0$
, this reduces to finding a
$S_0$
, this reduces to finding a
![]() $(k,1;\;s)$
-cover within
$(k,1;\;s)$
-cover within
![]() $S_0 \cong{\mathbb{F}_{2}^{n-d+1}}$
. By definition, we can find such a cover consisting of
$S_0 \cong{\mathbb{F}_{2}^{n-d+1}}$
. By definition, we can find such a cover consisting of
![]() $g(n-d+1,k,1;\;s)$
subspaces. Adding these to our previous multiset gives a
$g(n-d+1,k,1;\;s)$
subspaces. Adding these to our previous multiset gives a
![]() $(k,d;\;s)$
-cover of
$(k,d;\;s)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
of size
$\mathbb{F}_{2}^{n}$
of size
![]() $g(n-d+1,k,1;\;s) + 2k(2^{d-1} - 1)$
, as required.
$g(n-d+1,k,1;\;s) + 2k(2^{d-1} - 1)$
, as required.
To finish, since
![]() $f(n,k,d)=\min _s g(n,k,d;\;s)$
, and the recursive bound holds for each
$f(n,k,d)=\min _s g(n,k,d;\;s)$
, and the recursive bound holds for each
![]() $s$
, it naturally carries over to the function
$s$
, it naturally carries over to the function
![]() $f(n,k,d)$
, giving
$f(n,k,d)$
, giving
![]() .
.
Armed with this preparation, we can now resolve the problem for large multiplicities.
Proof of Theorem 1.2(a). The requisite lower bound, of course, is given by Lemma 2.1.
For the upper bound, we start by reducing to the case
![]() $d = 1$
. Indeed, suppose we already know the bound for
$d = 1$
. Indeed, suppose we already know the bound for
![]() $d=1$
; that is,
$d=1$
; that is,
![]() $f(n,k,1) \le 2k - \left\lfloor{ \frac{k}{2^{n-1}}}\right\rfloor$
for all
$f(n,k,1) \le 2k - \left\lfloor{ \frac{k}{2^{n-1}}}\right\rfloor$
for all
![]() $k \ge 2^{n-2}$
. Now, given some
$k \ge 2^{n-2}$
. Now, given some
![]() $n \ge d \ge 2$
and
$n \ge d \ge 2$
and
![]() $k \ge 2^{n-d-1}$
, by Lemma 2.2 we have
$k \ge 2^{n-d-1}$
, by Lemma 2.2 we have
as required.
Hence, it suffices to prove the bound in the hyperplane case. We begin with the lowest multiplicity covered by part (a), namely
![]() $k = 2^{n-2}$
. Consider the family
$k = 2^{n-2}$
. Consider the family
![]() $\mathcal{H}_0 = \{ H_{\vec{u}} \;:\; \vec{u} \in{\mathbb{F}_{2}^{n}}, u_n = 1 \}$
, where we recall that
$\mathcal{H}_0 = \{ H_{\vec{u}} \;:\; \vec{u} \in{\mathbb{F}_{2}^{n}}, u_n = 1 \}$
, where we recall that
![]() $H_{\vec{u}} = \{ \vec{x} \;:\; \vec{x} \cdot \vec{u} = 1 \}$
. Note that we then have
$H_{\vec{u}} = \{ \vec{x} \;:\; \vec{x} \cdot \vec{u} = 1 \}$
. Note that we then have
![]() $|{\mathcal{H}_0}| = 2^{n-1} = 2k = 2k - \left\lfloor{\frac{k}{2^{n-1}}}\right\rfloor$
, and none of these hyperplanes covers the origin. Given nonzero vectors
$|{\mathcal{H}_0}| = 2^{n-1} = 2k = 2k - \left\lfloor{\frac{k}{2^{n-1}}}\right\rfloor$
, and none of these hyperplanes covers the origin. Given nonzero vectors
![]() $\vec{x} = (\vec{x}', x)$
and
$\vec{x} = (\vec{x}', x)$
and
![]() $\vec{u} = (\vec{u}',1)$
with
$\vec{u} = (\vec{u}',1)$
with
![]() $\vec{x}', \vec{u}' \in{\mathbb{F}_{2}^{n-1}}$
and
$\vec{x}', \vec{u}' \in{\mathbb{F}_{2}^{n-1}}$
and
![]() $x \in{\mathbb{F}_{2}^{}}$
, we have
$x \in{\mathbb{F}_{2}^{}}$
, we have
![]() $\vec{x} \cdot \vec{u} = 1$
if and only if
$\vec{x} \cdot \vec{u} = 1$
if and only if
![]() $\vec{x}' \cdot \vec{u}' = 1-x$
. If
$\vec{x}' \cdot \vec{u}' = 1-x$
. If
![]() $\vec{x}' \neq \vec{0}$
, precisely half of the choices for
$\vec{x}' \neq \vec{0}$
, precisely half of the choices for
![]() $\vec{u}'$
satisfy this equation; if
$\vec{u}'$
satisfy this equation; if
![]() $\vec{x}' = \vec{0}$
(and thus necessarily
$\vec{x}' = \vec{0}$
(and thus necessarily
![]() $x = 1$
), the equation is satisfied by all choices of
$x = 1$
), the equation is satisfied by all choices of
![]() $\vec{u}'$
. Thus each nonzero point is covered at least
$\vec{u}'$
. Thus each nonzero point is covered at least
![]() $2^{n-2}$
times, and hence
$2^{n-2}$
times, and hence
![]() $\mathcal{H}_0$
is a
$\mathcal{H}_0$
is a
![]() $(2^{n-2},1)$
-cover of the desired size.
$(2^{n-2},1)$
-cover of the desired size.
To extend the above construction to the range
![]() $2^{n-2}\leq k\lt 2^{n-1}$
, one can simply add an arbitrary choice of
$2^{n-2}\leq k\lt 2^{n-1}$
, one can simply add an arbitrary choice of
![]() $k-2^{n-2}$
pairs of parallel hyperplanes. The resulting family will have
$k-2^{n-2}$
pairs of parallel hyperplanes. The resulting family will have
![]() $2^{n-1}+2\left (k-2^{n-2}\right )=2k=2k - \left\lfloor{\frac{k}{2^{n-1}}}\right\rfloor$
elements, every nonzero point is covered at least
$2^{n-1}+2\left (k-2^{n-2}\right )=2k=2k - \left\lfloor{\frac{k}{2^{n-1}}}\right\rfloor$
elements, every nonzero point is covered at least
![]() $k$
times, and the origin is covered
$k$
times, and the origin is covered
![]() $k-2^{n-2}\lt k$
times.
$k-2^{n-2}\lt k$
times.
Finally, suppose
![]() $k\geq 2^{n-1}$
. Then we can write
$k\geq 2^{n-1}$
. Then we can write
![]() $k = a2^{n-1}+b$
for some
$k = a2^{n-1}+b$
for some
![]() $a\geq 1$
and
$a\geq 1$
and
![]() $0\leq b \lt 2^{n-1}$
. We take
$0\leq b \lt 2^{n-1}$
. We take
![]() $\mathcal{H}_1 = \{ H_{\vec{u}} \;:\; \vec{u} \in{\mathbb{F}_{2}^{n}} \setminus \{\vec{0}\} \}$
to be the set of all affine hyperplanes avoiding the origin, of which there are
$\mathcal{H}_1 = \{ H_{\vec{u}} \;:\; \vec{u} \in{\mathbb{F}_{2}^{n}} \setminus \{\vec{0}\} \}$
to be the set of all affine hyperplanes avoiding the origin, of which there are
![]() $2^n-1$
. Moreover, for each nonzero
$2^n-1$
. Moreover, for each nonzero
![]() $\vec{x}$
, there are exactly
$\vec{x}$
, there are exactly
![]() $2^{n-1}$
vectors
$2^{n-1}$
vectors
![]() $\vec{u}$
with
$\vec{u}$
with
![]() $\vec{x} \cdot \vec{u} = 1$
, and so each such point is covered
$\vec{x} \cdot \vec{u} = 1$
, and so each such point is covered
![]() $2^{n-1}$
times by the hyperplanes in
$2^{n-1}$
times by the hyperplanes in
![]() $\mathcal{H}_1$
.
$\mathcal{H}_1$
.
Now let
![]() $\mathcal{H}$
be the multiset of hyperplanes obtained by taking
$\mathcal{H}$
be the multiset of hyperplanes obtained by taking
![]() $a$
copies of
$a$
copies of
![]() $\mathcal{H}_1$
and appending an arbitrary choice of
$\mathcal{H}_1$
and appending an arbitrary choice of
![]() $b$
pairs of parallel planes. Each nonzero point is then covered
$b$
pairs of parallel planes. Each nonzero point is then covered
![]() $a2^{n-1} + b = k$
times, while the origin is only covered
$a2^{n-1} + b = k$
times, while the origin is only covered
![]() $b \lt 2^{n-1} \le k$
times, and so
$b \lt 2^{n-1} \le k$
times, and so
![]() $\mathcal{H}$
is a
$\mathcal{H}$
is a
![]() $(k,1)$
-cover. Thus,
$(k,1)$
-cover. Thus,
proving the upper bound.
3. Covering high-dimensional spaces
In this section we turn our attention to the case when
![]() $n$
is large with respect to
$n$
is large with respect to
![]() $k$
, with the aim of proving part (b) of Theorem 1.2. Furthermore, the results we prove along the way will allow us to establish the bounds in part (c) as well.
$k$
, with the aim of proving part (b) of Theorem 1.2. Furthermore, the results we prove along the way will allow us to establish the bounds in part (c) as well.
3.1. The upper bound construction
In this range, in contrast to the large multiplicity setting, it is the upper bound that is straightforward. This bound follows from the following construction, which is valid for the full range of parameters.
Lemma 3.1.
Let
![]() $n,k,d$
be positive integers such that
$n,k,d$
be positive integers such that
![]() $n \ge d \ge 1$
and
$n \ge d \ge 1$
and
![]() $k \ge 2$
. Then
$k \ge 2$
. Then
Proof. We start by resolving the case
![]() $d=1$
and
$d=1$
and
![]() $k=2$
, for which we consider the family of hyperplanes
$k=2$
, for which we consider the family of hyperplanes
![]() $\mathcal{H} = \{ H_{\vec{e}_i} \;:\; i\in [n] \}\cup \{H_{\vec{1}}\}$
, where
$\mathcal{H} = \{ H_{\vec{e}_i} \;:\; i\in [n] \}\cup \{H_{\vec{1}}\}$
, where
![]() $\vec{e}_i$
is the
$\vec{e}_i$
is the
![]() $i$
th standard basis vector and
$i$
th standard basis vector and
![]() $\vec{1}$
is the all-one vector. To see that this is a
$\vec{1}$
is the all-one vector. To see that this is a
![]() $(2,1$
)-cover of
$(2,1$
)-cover of
![]() $\mathbb{F}_{2}^{n}$
, note first that the planes all avoid the origin. Next, if we have a nonzero vector
$\mathbb{F}_{2}^{n}$
, note first that the planes all avoid the origin. Next, if we have a nonzero vector
![]() $\vec{x}$
, it is covered by the hyperplanes
$\vec{x}$
, it is covered by the hyperplanes
![]() $\{ H_{\vec{e}_i} \;:\; i\in [n] \}$
as many times as it has nonzero entries. Thus, all vectors of Hamming weight at least two are covered twice or more. The only remaining vectors are those of weight one, which are covered once by
$\{ H_{\vec{e}_i} \;:\; i\in [n] \}$
as many times as it has nonzero entries. Thus, all vectors of Hamming weight at least two are covered twice or more. The only remaining vectors are those of weight one, which are covered once by
![]() $\{ H_{\vec{e}_i} \;:\; i\in [n] \}$
, but these are all covered for the second time by
$\{ H_{\vec{e}_i} \;:\; i\in [n] \}$
, but these are all covered for the second time by
![]() $H_{\vec{1}}$
. Hence
$H_{\vec{1}}$
. Hence
![]() $\mathcal{H}$
is indeed a
$\mathcal{H}$
is indeed a
![]() $(2,1)$
-cover, and is of the required size, namely
$(2,1)$
-cover, and is of the required size, namely
![]() $n+1$
.
$n+1$
.
Now we can extend this construction to the case
![]() $d=1$
and
$d=1$
and
![]() $k\geq 3$
by simply adding
$k\geq 3$
by simply adding
![]() $k-2$
arbitrary pairs of parallel hyperplanes. The resulting family will be a
$k-2$
arbitrary pairs of parallel hyperplanes. The resulting family will be a
![]() $(k,1;\;k-2)$
-cover (and hence, in particular, a
$(k,1;\;k-2)$
-cover (and hence, in particular, a
![]() $(k,1)$
-cover) of size
$(k,1)$
-cover) of size
![]() $n+2k-3$
, matching the claimed upper bound.
$n+2k-3$
, matching the claimed upper bound.
That leaves us with the case
![]() $d \ge 2$
, which we can once again handle by appealing to Lemma 2.2. In conjunction with the above construction, we have
$d \ge 2$
, which we can once again handle by appealing to Lemma 2.2. In conjunction with the above construction, we have
which simplifies to the required
![]() $n + 2^d k - d - 2$
.
$n + 2^d k - d - 2$
.
3.2. Recursion, again
The upper bound in Lemma 3.1 is strictly increasing in
![]() $n$
. Our next step is to show that this behaviour is necessary—that is, the higher the dimension, the harder the space is to cover. Although intuitive, this fact turned out to be less elementary than expected, and our proof makes use of the probabilistic method.
$n$
. Our next step is to show that this behaviour is necessary—that is, the higher the dimension, the harder the space is to cover. Although intuitive, this fact turned out to be less elementary than expected, and our proof makes use of the probabilistic method.
Lemma 3.2.
Let
![]() $n,k,d,s$
be integers such that
$n,k,d,s$
be integers such that
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $n \ge d \ge 1$
, and
$n \ge d \ge 1$
, and
![]() $k \gt s \ge 0$
. Then
$k \gt s \ge 0$
. Then
Proof. Let
![]() $\mathcal{H}$
be an optimal
$\mathcal{H}$
be an optimal
![]() $(k,d;\;s)$
-cover of
$(k,d;\;s)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
. To prove the lower bound on its size, we shall construct from it a
$\mathbb{F}_{2}^{n}$
. To prove the lower bound on its size, we shall construct from it a
![]() $(k,d;\;s)$
-cover
$(k,d;\;s)$
-cover
![]() $\mathcal{H}'$
of
$\mathcal{H}'$
of
![]() $\mathbb{F}_{2}^{n-1}$
, which must comprise of at least
$\mathbb{F}_{2}^{n-1}$
, which must comprise of at least
![]() $g(n-1,k,d;\;s)$
subspaces. To obtain this cover of a lower-dimensional space, we restrict
$g(n-1,k,d;\;s)$
subspaces. To obtain this cover of a lower-dimensional space, we restrict
![]() $\mathcal{H}$
to a random hyperplane
$\mathcal{H}$
to a random hyperplane
![]() $H \subseteq{\mathbb{F}_{2}^{n}}$
that passes through the origin. Since
$H \subseteq{\mathbb{F}_{2}^{n}}$
that passes through the origin. Since
![]() $\mathcal{H}$
is a
$\mathcal{H}$
is a
![]() $(k,d;\;s)$
-cover of all of
$(k,d;\;s)$
-cover of all of
![]() $\mathbb{F}_{2}^{n}$
, it certainly covers
$\mathbb{F}_{2}^{n}$
, it certainly covers
![]() $H \cong{\mathbb{F}_{2}^{n-1}}$
as well.
$H \cong{\mathbb{F}_{2}^{n-1}}$
as well.
However, we require
![]() $\mathcal{H}'$
to be a
$\mathcal{H}'$
to be a
![]() $(k,d;\;s)$
-cover of
$(k,d;\;s)$
-cover of
![]() $H$
, which must be built of affine subspaces of codimension
$H$
, which must be built of affine subspaces of codimension
![]() $d$
relative to
$d$
relative to
![]() $H$
—that is, subspaces of dimension one less than those in
$H$
—that is, subspaces of dimension one less than those in
![]() $\mathcal{H}$
. Fortunately, when intersecting the subspaces
$\mathcal{H}$
. Fortunately, when intersecting the subspaces
![]() $S \in \mathcal{H}$
with a hyperplane, we can expect their dimension to decrease by one. The exceptional cases are when
$S \in \mathcal{H}$
with a hyperplane, we can expect their dimension to decrease by one. The exceptional cases are when
![]() $S$
is disjoint from
$S$
is disjoint from
![]() $H$
, or when
$H$
, or when
![]() $S$
is contained in
$S$
is contained in
![]() $H$
. In the former case,
$H$
. In the former case,
![]() $S$
does not cover any points of
$S$
does not cover any points of
![]() $H$
, and can therefore be discarded from
$H$
, and can therefore be discarded from
![]() $\mathcal{H}'$
. In the latter case, we can partition
$\mathcal{H}'$
. In the latter case, we can partition
![]() $S$
into two subspaces
$S$
into two subspaces
![]() $S = S_1 \cup S_2$
, where each
$S = S_1 \cup S_2$
, where each
![]() $S_i$
is of codimension
$S_i$
is of codimension
![]() $d$
relative to
$d$
relative to
![]() $H$
, and replace
$H$
, and replace
![]() $S$
with
$S$
with
![]() $S_1$
and
$S_1$
and
![]() $S_2$
in
$S_2$
in
![]() $\mathcal{H}'$
. By making these changes, we obtain a family
$\mathcal{H}'$
. By making these changes, we obtain a family
![]() $\mathcal{H}'$
of codimension-
$\mathcal{H}'$
of codimension-
![]() $d$
subspaces of
$d$
subspaces of
![]() $H$
. Moreover, these subspaces cover the points of
$H$
. Moreover, these subspaces cover the points of
![]() $H$
exactly as often as those of
$H$
exactly as often as those of
![]() $\mathcal{H}$
do, and thus
$\mathcal{H}$
do, and thus
![]() $\mathcal{H}'$
is a
$\mathcal{H}'$
is a
![]() $(k,d;\;s)$
-cover of
$(k,d;\;s)$
-cover of
![]() $H$
.
$H$
.
When building this cover, though, we need to control its size. Let
![]() $X$
denote the set of subspaces
$X$
denote the set of subspaces
![]() $S \in \mathcal{H}$
that are disjoint from
$S \in \mathcal{H}$
that are disjoint from
![]() $H$
, and let
$H$
, and let
![]() $Y$
denote the set of subspaces
$Y$
denote the set of subspaces
![]() $S \in \mathcal{H}$
that are contained in
$S \in \mathcal{H}$
that are contained in
![]() $H$
. We then have
$H$
. We then have
![]() $|{ \mathcal{H}'}| = |{\mathcal{H}}| - |{X}| + |{Y}|$
. The objective, then, is to show that there is a choice of hyperplane
$|{ \mathcal{H}'}| = |{\mathcal{H}}| - |{X}| + |{Y}|$
. The objective, then, is to show that there is a choice of hyperplane
![]() $H$
for which
$H$
for which
![]() $|{X}| \gt |{Y}|$
, in which case the cover
$|{X}| \gt |{Y}|$
, in which case the cover
![]() $\mathcal{H}'$
we build is relatively small.
$\mathcal{H}'$
we build is relatively small.
Recall that
![]() $H$
was a random hyperplane in
$H$
was a random hyperplane in
![]() $\mathbb{F}_{2}^{n}$
passing through the origin, which is to say it has a normal vector
$\mathbb{F}_{2}^{n}$
passing through the origin, which is to say it has a normal vector
![]() $\vec{u}$
chosen uniformly at random from
$\vec{u}$
chosen uniformly at random from
![]() ${\mathbb{F}_{2}^{n}}\setminus \{\vec{0}\}$
. To compute the expected sizes of
${\mathbb{F}_{2}^{n}}\setminus \{\vec{0}\}$
. To compute the expected sizes of
![]() $X$
and
$X$
and
![]() $Y$
, we consider the probability that a subspace
$Y$
, we consider the probability that a subspace
![]() $S \in \mathcal{H}$
is either disjoint from or contained in
$S \in \mathcal{H}$
is either disjoint from or contained in
![]() $H$
.
$H$
.
Let
![]() $S\in \mathcal{H}$
be arbitrary and suppose first that
$S\in \mathcal{H}$
be arbitrary and suppose first that
![]() $\vec{0}\in S$
. We immediately have
$\vec{0}\in S$
. We immediately have
![]() $\mathbb{P}(S\in X)=0$
, as in this case
$\mathbb{P}(S\in X)=0$
, as in this case
![]() $\vec{0}\in S\cap H$
, so
$\vec{0}\in S\cap H$
, so
![]() $S$
and
$S$
and
![]() $H$
cannot be disjoint. On the other hand,
$H$
cannot be disjoint. On the other hand,
![]() $\mathbb{P}(S\in Y)=\frac{2^d-1}{2^{n}-1}$
, as we have
$\mathbb{P}(S\in Y)=\frac{2^d-1}{2^{n}-1}$
, as we have
![]() $S\subseteq H$
exactly when the normal vector
$S\subseteq H$
exactly when the normal vector
![]() $\vec{u}$
is a nonzero element of the
$\vec{u}$
is a nonzero element of the
![]() $d$
-dimensional orthogonal complement,
$d$
-dimensional orthogonal complement,
![]() $S^{\perp }$
, of
$S^{\perp }$
, of
![]() $S$
in
$S$
in
![]() $\mathbb{F}_{2}^{n}$
.
$\mathbb{F}_{2}^{n}$
.
In the other case, when
![]() $\vec{0}\notin S$
, we can write
$\vec{0}\notin S$
, we can write
![]() $S$
in the form
$S$
in the form
![]() $T+\vec{v}$
, where
$T+\vec{v}$
, where
![]() $\vec{0} \in T \subseteq{\mathbb{F}_{2}^{n}}$
is an
$\vec{0} \in T \subseteq{\mathbb{F}_{2}^{n}}$
is an
![]() $(n-d)$
-dimensional vector subspace and
$(n-d)$
-dimensional vector subspace and
![]() $\vec{v} \in{\mathbb{F}_{2}^{n}}\setminus T$
. Then
$\vec{v} \in{\mathbb{F}_{2}^{n}}\setminus T$
. Then
![]() $S$
is disjoint from
$S$
is disjoint from
![]() $H$
if and only if
$H$
if and only if
![]() $\vec{u} \in T^{\perp }$
and
$\vec{u} \in T^{\perp }$
and
![]() $\vec{u} \cdot \vec{v} = 1$
. Since
$\vec{u} \cdot \vec{v} = 1$
. Since
![]() $\vec{v} \notin T$
, these are independent conditions, and so we have
$\vec{v} \notin T$
, these are independent conditions, and so we have
![]() $\mathbb{P}(S \in X)=\frac{2^{d-1}}{2^{n}-1}$
. Similarly, in order to have
$\mathbb{P}(S \in X)=\frac{2^{d-1}}{2^{n}-1}$
. Similarly, in order to have
![]() $S \subseteq H$
,
$S \subseteq H$
,
![]() $\vec{u}$
must be a nonzero vector satisfying
$\vec{u}$
must be a nonzero vector satisfying
![]() $\vec{u} \in T^{\perp }$
and
$\vec{u} \in T^{\perp }$
and
![]() $\vec{u} \cdot \vec{v} = 0$
, and so
$\vec{u} \cdot \vec{v} = 0$
, and so
![]() $\mathbb{P}(S\in Y)=\frac{2^{d-1}-1}{2^{n}-1}$
.
$\mathbb{P}(S\in Y)=\frac{2^{d-1}-1}{2^{n}-1}$
.
Now, using linearity of expectation, we have
 \begin{align*} \mathbb{E} \left [ |{X}| - |{Y}| \right ] &= \sum _{S\in \mathcal{H}} \left (\mathbb{P}(S\in X)-\mathbb{P}(S\in Y)\right )\\[5pt] &= \sum _{S\in \mathcal{H}:\vec{0}\notin S} \left (\frac{2^{d-1}}{2^{n}-1}-\frac{2^{d-1}-1}{2^{n}-1}\right ) + \sum _{S\in \mathcal{H}:\vec{0}\in S} \left (0-\frac{2^d-1}{2^{n}-1}\right ) \\[5pt] &=\frac{|{\{S\in \mathcal{H}\;:\; \vec{0}\notin S\}}|-\left (2^d-1\right )|{\{S\in \mathcal{H}\;:\; \vec{0}\in S\}}|}{2^n-1} =\frac{|{\mathcal{H}}| - 2^d s}{2^n-1}, \end{align*}
\begin{align*} \mathbb{E} \left [ |{X}| - |{Y}| \right ] &= \sum _{S\in \mathcal{H}} \left (\mathbb{P}(S\in X)-\mathbb{P}(S\in Y)\right )\\[5pt] &= \sum _{S\in \mathcal{H}:\vec{0}\notin S} \left (\frac{2^{d-1}}{2^{n}-1}-\frac{2^{d-1}-1}{2^{n}-1}\right ) + \sum _{S\in \mathcal{H}:\vec{0}\in S} \left (0-\frac{2^d-1}{2^{n}-1}\right ) \\[5pt] &=\frac{|{\{S\in \mathcal{H}\;:\; \vec{0}\notin S\}}|-\left (2^d-1\right )|{\{S\in \mathcal{H}\;:\; \vec{0}\in S\}}|}{2^n-1} =\frac{|{\mathcal{H}}| - 2^d s}{2^n-1}, \end{align*}
where we used the fact that
![]() $\mathcal{H}$
is a
$\mathcal{H}$
is a
![]() $(k,d;\;s)$
-cover, and thus
$(k,d;\;s)$
-cover, and thus
![]() $|{\{S \in \mathcal{H}\;:\; \vec{0} \in S \}}| = s$
. We now apply the lower bound on
$|{\{S \in \mathcal{H}\;:\; \vec{0} \in S \}}| = s$
. We now apply the lower bound on
![]() $|{\mathcal{H}}|$
given by Lemma 2.1 to obtain
$|{\mathcal{H}}|$
given by Lemma 2.1 to obtain
 \begin{equation*} \mathbb {E} \left [ |{X}| - |{Y}| \right ] \geq \frac {2^d k - \left\lfloor {\frac {k-s}{2^{n-d}}}\right\rfloor -2^d s}{2^n-1} = \frac {2^d (k-s) - \left\lfloor {\frac {k-s}{2^{n-d}}}\right\rfloor }{2^n-1}\gt 0. \end{equation*}
\begin{equation*} \mathbb {E} \left [ |{X}| - |{Y}| \right ] \geq \frac {2^d k - \left\lfloor {\frac {k-s}{2^{n-d}}}\right\rfloor -2^d s}{2^n-1} = \frac {2^d (k-s) - \left\lfloor {\frac {k-s}{2^{n-d}}}\right\rfloor }{2^n-1}\gt 0. \end{equation*}
Therefore, there must be a hyperplane
![]() $H$
for which
$H$
for which
![]() $|{X}| - |{Y}| \ge 1$
. The corresponding cover of
$|{X}| - |{Y}| \ge 1$
. The corresponding cover of
![]() $H$
thus has size at most
$H$
thus has size at most
![]() $|{\mathcal{H}}| - 1$
but, as a
$|{\mathcal{H}}| - 1$
but, as a
![]() $(k,d;\;s)$
-cover of an
$(k,d;\;s)$
-cover of an
![]() $(n-1)$
-dimensional space, has size at least
$(n-1)$
-dimensional space, has size at least
![]() $g(n-1,k,d;\;s)$
. This gives
$g(n-1,k,d;\;s)$
. This gives
![]() $|{\mathcal{H}}| - 1 \ge |{\mathcal{H}'}| \ge g(n-1,k,d;\;s)$
, whence the required bound,
$|{\mathcal{H}}| - 1 \ge |{\mathcal{H}'}| \ge g(n-1,k,d;\;s)$
, whence the required bound,
![]() $g(n,k,d;\;s) = |{\mathcal{H}}| \ge g(n-1,k,d;\;s) + 1$
.
$g(n,k,d;\;s) = |{\mathcal{H}}| \ge g(n-1,k,d;\;s) + 1$
.
While this inequality will be used in our proof of part (b) of Theorem 1.2, it also gives us what we need to prove the bounds in part (c).
Proof of Theorem
1.2(c). Lemma 3.1 gives us the upper bound,
![]() $f(n,k,d) \le n + 2^d k - d -2$
, which is in fact valid for all
$f(n,k,d) \le n + 2^d k - d -2$
, which is in fact valid for all
![]() $k \ge 2$
and
$k \ge 2$
and
![]() $n \ge d \ge 1$
.
$n \ge d \ge 1$
.
When
![]() $n \ge \lfloor{\log _2 k}\rfloor + d + 1$
, we can prove the lower bound,
$n \ge \lfloor{\log _2 k}\rfloor + d + 1$
, we can prove the lower bound,
![]() $f(n,k,d) \ge n + 2^d k - d - \log _2\!(2k)$
, by induction on
$f(n,k,d) \ge n + 2^d k - d - \log _2\!(2k)$
, by induction on
![]() $n$
. For the base case, when
$n$
. For the base case, when
![]() $n = \lfloor{\log _2 k}\rfloor + d + 1$
, we appeal to Lemma 2.1, which gives
$n = \lfloor{\log _2 k}\rfloor + d + 1$
, we appeal to Lemma 2.1, which gives
For the induction step we appeal to Lemma 3.2. First note that the lemma gives
![]() $f(n,k,d) = \min _s g(n,k,d;\;s) \ge \min _s\!( g(n-1,k,d;\;s) + 1 ) = f(n-1,k,d) + 1$
. Thus, using the induction hypothesis, for all
$f(n,k,d) = \min _s g(n,k,d;\;s) \ge \min _s\!( g(n-1,k,d;\;s) + 1 ) = f(n-1,k,d) + 1$
. Thus, using the induction hypothesis, for all
![]() $n \gt \lfloor{\log _2 k}\rfloor + d + 1$
we have
$n \gt \lfloor{\log _2 k}\rfloor + d + 1$
we have
completing the proof.
At this stage, all that remains to be proven from Theorem 1.2 is the lower bound of part (b), a task we undertake in the following subsections.
3.3. A coding theory connection
In Lemma 3.2, we proved a recursive bound on
![]() $g(n,k,d;\;s)$
that is valid for all values of
$g(n,k,d;\;s)$
that is valid for all values of
![]() $s$
, the number of times the origin is covered. In this subsection, we establish the promised connection to coding theory, which is the key to our proof. Indeed, as observed in Corollary 3.7 below, it allows us to restrict our attention to only two feasible values of
$s$
, the number of times the origin is covered. In this subsection, we establish the promised connection to coding theory, which is the key to our proof. Indeed, as observed in Corollary 3.7 below, it allows us to restrict our attention to only two feasible values of
![]() $s$
.
$s$
.
We begin with
![]() $(k,1;\;0)$
-covers of
$(k,1;\;0)$
-covers of
![]() $\mathbb{F}_{2}^{n}$
, showing that, in this binary setting, hyperplane covers that avoid the origin are in direct correspondence with linear codes of large minimum distance. In the setting of multiple blocking sets, this connection to coding theory was observed by Landjev and Rousseva [Reference Landjev and Rousseva21], who used it to show that Bruen’s bound is far from being tight over
$\mathbb{F}_{2}^{n}$
, showing that, in this binary setting, hyperplane covers that avoid the origin are in direct correspondence with linear codes of large minimum distance. In the setting of multiple blocking sets, this connection to coding theory was observed by Landjev and Rousseva [Reference Landjev and Rousseva21], who used it to show that Bruen’s bound is far from being tight over
![]() $\mathbb{F}_2$
. We use a similar idea to obtain concrete bounds for
$\mathbb{F}_2$
. We use a similar idea to obtain concrete bounds for
![]() $g(n,k,1;\;0)$
.
$g(n,k,1;\;0)$
.
Proposition 3.3.
A
![]() $(k,1;\;0)$
-cover of
$(k,1;\;0)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
of cardinality
$\mathbb{F}_{2}^{n}$
of cardinality
![]() $m$
is equivalent to an
$m$
is equivalent to an
![]() $n$
-dimensional linear binary code of length
$n$
-dimensional linear binary code of length
![]() $m$
and minimum distance at least
$m$
and minimum distance at least
![]() $k$
.
$k$
.
Remark 3.4. In order to maintain consistency with earlier papers on hyperplane coverings, we deviate slightly from the standard coding theoretic notation, where
![]() $n$
usually stands for the length of the code,
$n$
usually stands for the length of the code,
![]() $k$
for its dimension, and
$k$
for its dimension, and
![]() $d$
for its minimum distance. In other words, our codes are
$d$
for its minimum distance. In other words, our codes are
![]() $[m, n, k]$
-codes as opposed to the more standard
$[m, n, k]$
-codes as opposed to the more standard
![]() $[n,k,d]$
-codes.
$[n,k,d]$
-codes.
Proof. Let
![]() $\mathcal{H} = \{H_1, H_2, \ldots, H_m\}$
be a
$\mathcal{H} = \{H_1, H_2, \ldots, H_m\}$
be a
![]() $(k,1;\;0)$
-cover of
$(k,1;\;0)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
. Since none of the hyperplanes cover the origin, for each
$\mathbb{F}_{2}^{n}$
. Since none of the hyperplanes cover the origin, for each
![]() $i \in [m]$
,
$i \in [m]$
,
![]() $H_i$
has to be described by the equation
$H_i$
has to be described by the equation
![]() $\vec{u}_i\cdot \vec{x} = 1$
for some
$\vec{u}_i\cdot \vec{x} = 1$
for some
![]() $\vec{u}_i \in{\mathbb{F}_{2}^{n}} \setminus \{ \vec{0} \}$
. Let
$\vec{u}_i \in{\mathbb{F}_{2}^{n}} \setminus \{ \vec{0} \}$
. Let
![]() $A$
be the
$A$
be the
![]() $m \times n$
matrix whose rows are
$m \times n$
matrix whose rows are
![]() $\vec{u}_1, \vec{u}_2, \ldots, \vec{u}_m$
. We claim that
$\vec{u}_1, \vec{u}_2, \ldots, \vec{u}_m$
. We claim that
![]() $A$
is the generator matrix of a linear binary code of dimension
$A$
is the generator matrix of a linear binary code of dimension
![]() $n$
, length
$n$
, length
![]() $m$
, and minimum distance at least
$m$
, and minimum distance at least
![]() $k$
. Since each
$k$
. Since each
![]() $\vec{x} \in{\mathbb{F}_{2}^{n}} \setminus \{ \vec{0} \}$
is covered by at least
$\vec{x} \in{\mathbb{F}_{2}^{n}} \setminus \{ \vec{0} \}$
is covered by at least
![]() $k$
of the planes, it follows that the vector
$k$
of the planes, it follows that the vector
![]() $A \vec{x}$
has weight at least
$A \vec{x}$
has weight at least
![]() $k$
, which in turn is equivalent to the vectors in the column space of
$k$
, which in turn is equivalent to the vectors in the column space of
![]() $A$
having minimum distance at least
$A$
having minimum distance at least
![]() $k$
. Indeed, any vector
$k$
. Indeed, any vector
![]() $\vec{y}$
in the column space can be expressed in the form
$\vec{y}$
in the column space can be expressed in the form
![]() $A \vec{w}$
for some
$A \vec{w}$
for some
![]() $\vec{w} \in{\mathbb{F}_{2}^{n}}$
. Thus, given two distinct vectors
$\vec{w} \in{\mathbb{F}_{2}^{n}}$
. Thus, given two distinct vectors
![]() $\vec{y}_1, \vec{y}_2$
in the column space, their difference is of the form
$\vec{y}_1, \vec{y}_2$
in the column space, their difference is of the form
![]() $A(\vec{w}_1 - \vec{w}_2)$
, where
$A(\vec{w}_1 - \vec{w}_2)$
, where
![]() $\vec{x} = \vec{w}_1 - \vec{w}_2$
is nonzero. Hence this difference has weight at least
$\vec{x} = \vec{w}_1 - \vec{w}_2$
is nonzero. Hence this difference has weight at least
![]() $k$
; i.e., the two vectors
$k$
; i.e., the two vectors
![]() $\vec{y}_1$
and
$\vec{y}_1$
and
![]() $\vec{y}_2$
have distance at least
$\vec{y}_2$
have distance at least
![]() $k$
. The fact that the weight of
$k$
. The fact that the weight of
![]() $A\vec{x}$
is at least
$A\vec{x}$
is at least
![]() $k\geq 1$
for any
$k\geq 1$
for any
![]() $\vec{x}\neq 0$
also implies that the kernel of
$\vec{x}\neq 0$
also implies that the kernel of
![]() $A$
is trivial; therefore, the dimension of the column space of
$A$
is trivial; therefore, the dimension of the column space of
![]() $A$
, and hence of the binary code generated by
$A$
, and hence of the binary code generated by
![]() $A$
, is
$A$
, is
![]() $n$
.
$n$
.
Conversely, given a linear binary code of dimension
![]() $n$
, length
$n$
, length
![]() $m$
, and minimum distance at least
$m$
, and minimum distance at least
![]() $k$
, let
$k$
, let
![]() $\vec{u}_1, \vec{u}_2, \ldots, \vec{u}_m$
be the rows of the generator matrix. By the same reasoning as above, the hyperplanes
$\vec{u}_1, \vec{u}_2, \ldots, \vec{u}_m$
be the rows of the generator matrix. By the same reasoning as above, the hyperplanes
![]() $H_i$
,
$H_i$
,
![]() $i\in [m]$
, defined by the equation
$i\in [m]$
, defined by the equation
![]() $\vec{u}_i\cdot \vec{x} = 1$
, form a
$\vec{u}_i\cdot \vec{x} = 1$
, form a
![]() $(k,1;\;0)$
-cover of
$(k,1;\;0)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
.
$\mathbb{F}_{2}^{n}$
.
Thus, the problem of finding a small
![]() $(k,1;\;0)$
-cover of
$(k,1;\;0)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
corresponds to finding an
$\mathbb{F}_{2}^{n}$
corresponds to finding an
![]() $n$
-dimensional linear code of minimum distance at least
$n$
-dimensional linear code of minimum distance at least
![]() $k$
and small length. This is a central problem in coding theory [Reference van Lint14] and, as such, has been extensively studied (see for example [Reference Jiang and Vardy17, Reference Schrijver25] and the references therein). We can therefore leverage known bounds to bound the function
$k$
and small length. This is a central problem in coding theory [Reference van Lint14] and, as such, has been extensively studied (see for example [Reference Jiang and Vardy17, Reference Schrijver25] and the references therein). We can therefore leverage known bounds to bound the function
![]() $g(n,k,1;\;0)$
.
$g(n,k,1;\;0)$
.
Corollary 3.5.
For all
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $n \geq 1$
,
$n \geq 1$
,
Proof. Let
![]() $\mathcal{H}$
be an optimal
$\mathcal{H}$
be an optimal
![]() $(k,1,0)$
-cover and let
$(k,1,0)$
-cover and let
![]() $\mathcal{C} \subseteq{\mathbb{F}_{2}^{m}}$
be the equivalent
$\mathcal{C} \subseteq{\mathbb{F}_{2}^{m}}$
be the equivalent
![]() $n$
-dimensional linear binary code of length
$n$
-dimensional linear binary code of length
![]() $m=|{\mathcal{H}}|$
and minimum distance at least
$m=|{\mathcal{H}}|$
and minimum distance at least
![]() $k$
, as described in Proposition 3.3. We can now appeal to the Hamming bound: since the code has minimum distance
$k$
, as described in Proposition 3.3. We can now appeal to the Hamming bound: since the code has minimum distance
![]() $k$
, the balls of radius
$k$
, the balls of radius
![]() $t = \left\lfloor{\frac{k-1}{2}}\right\rfloor$
around the
$t = \left\lfloor{\frac{k-1}{2}}\right\rfloor$
around the
![]() $2^n$
points of
$2^n$
points of
![]() $\mathcal{C}$
must be pairwise disjoint. As each ball has size
$\mathcal{C}$
must be pairwise disjoint. As each ball has size
![]() $\sum _{i=0}^t \binom{m}{i}$
, and the ambient space has size
$\sum _{i=0}^t \binom{m}{i}$
, and the ambient space has size
![]() $2^m$
, we get
$2^m$
, we get
We bound the denominator from below by
 \begin{equation*} \sum _{i=0}^t \binom {m}{i}\geq \binom {m}{t} \ge \left ( \frac {m}{t} \right )^t \ge \left ( \frac {n}{t} \right )^t = 2^{t \log _2 \left (\tfrac {n}{t}\right )}, \end{equation*}
\begin{equation*} \sum _{i=0}^t \binom {m}{i}\geq \binom {m}{t} \ge \left ( \frac {m}{t} \right )^t \ge \left ( \frac {n}{t} \right )^t = 2^{t \log _2 \left (\tfrac {n}{t}\right )}, \end{equation*}
where the last inequality is valid provided
![]() $m\geq n$
, as it must be. Thus we conclude
$m\geq n$
, as it must be. Thus we conclude
Remark 3.6. Although it may seem that some of our bounds might be wasteful, one can deduce upper bounds from the Gilbert–Varshamov bound, which is obtained by considering a random linear code. In particular, if
![]() $n$
is large with respect to
$n$
is large with respect to
![]() $k$
, one finds that
$k$
, one finds that
![]() . Narrowing the gap between these upper and lower bounds remains an active area of research in coding theory.
. Narrowing the gap between these upper and lower bounds remains an active area of research in coding theory.
The above lower bound can be used to show that, if
![]() $n$
is large with respect to
$n$
is large with respect to
![]() $k$
and
$k$
and
![]() $d$
, then every optimal
$d$
, then every optimal
![]() $(k,d)$
-cover has to cover the origin many times. This corollary is critical to our proof of the upper bound.
$(k,d)$
-cover has to cover the origin many times. This corollary is critical to our proof of the upper bound.
Corollary 3.7.
If
![]() $n \gt 2^{2^d k -k-d+ 1}$
, then any optimal
$n \gt 2^{2^d k -k-d+ 1}$
, then any optimal
![]() $(k,d)$
-cover of
$(k,d)$
-cover of
![]() $\mathbb{F}_2^n$
covers the origin at least
$\mathbb{F}_2^n$
covers the origin at least
![]() $k-2$
times.
$k-2$
times.
Proof. Let
![]() $S_1, \dots, S_m$
be an optimal
$S_1, \dots, S_m$
be an optimal
![]() $(k,d)$
-cover, and, if necessary, relabel the subspaces so that
$(k,d)$
-cover, and, if necessary, relabel the subspaces so that
![]() $S_1, \dots, S_s$
are the affine subspaces covering the origin. Suppose for a contradiction that
$S_1, \dots, S_s$
are the affine subspaces covering the origin. Suppose for a contradiction that
![]() $s \leq k - 3$
, and observe that if we delete the first
$s \leq k - 3$
, and observe that if we delete the first
![]() $k-3$
subspaces, each nonzero point must still be covered at least thrice, while the origin is left uncovered. That is,
$k-3$
subspaces, each nonzero point must still be covered at least thrice, while the origin is left uncovered. That is,
![]() $S_{k-2}, S_{k-1}, \ldots, S_m$
forms a
$S_{k-2}, S_{k-1}, \ldots, S_m$
forms a
![]() $(3,d;\;0)$
-cover of
$(3,d;\;0)$
-cover of
![]() $\mathbb{F}_{2}^{n}$
.
$\mathbb{F}_{2}^{n}$
.
For each
![]() $k-2 \le j \le m$
, we can then extend
$k-2 \le j \le m$
, we can then extend
![]() $S_j$
to an arbitrary hyperplane
$S_j$
to an arbitrary hyperplane
![]() $H_j$
that contains
$H_j$
that contains
![]() $S_j$
and avoids the origin. Then
$S_j$
and avoids the origin. Then
![]() $\{H_{k-2}, H_{k-1}, \ldots, H_m\}$
is a
$\{H_{k-2}, H_{k-1}, \ldots, H_m\}$
is a
![]() $(3,1;\;0)$
-cover, and hence
$(3,1;\;0)$
-cover, and hence
![]() $m-k+3 \ge g(n,3,1;\;0)$
.
$m-k+3 \ge g(n,3,1;\;0)$
.
By Corollary 3.5, this, together with the assumption
![]() $n \gt 2^{2^d k -k-d+ 1}$
, implies
$n \gt 2^{2^d k -k-d+ 1}$
, implies
 \begin{align*} f(n,k,d)&=m\geq g(n,3,1;\;0)+k-3\geq n +\log _2 n + k-3\gt n + 2^d k -k-d+ 1+k-3\\[5pt] &= n + 2^d k - d - 2, \end{align*}
\begin{align*} f(n,k,d)&=m\geq g(n,3,1;\;0)+k-3\geq n +\log _2 n + k-3\gt n + 2^d k -k-d+ 1+k-3\\[5pt] &= n + 2^d k - d - 2, \end{align*}
which contradicts the upper bound from Lemma 3.1.
Remark 3.8. Observe that Corollary 3.7 in fact gives us some stability for large dimensions. If
![]() $n = 2^{2^d k - k - d + \omega (1)}$
, then the above calculation shows that any
$n = 2^{2^d k - k - d + \omega (1)}$
, then the above calculation shows that any
![]() $(k,d)$
-cover that covers the origin at most
$(k,d)$
-cover that covers the origin at most
![]() $k-3$
times has size at least
$k-3$
times has size at least
![]() $n + 2^d k + \omega (1)$
. Thus, when
$n + 2^d k + \omega (1)$
. Thus, when
![]() $n = 2^{2^d k - k - d + \omega (1)}$
, any
$n = 2^{2^d k - k - d + \omega (1)}$
, any
![]() $(k,d)$
-cover that is even close to optimal must cover the origin at least
$(k,d)$
-cover that is even close to optimal must cover the origin at least
![]() $k-2$
times.
$k-2$
times.
3.4. The lower bound
By Corollary 3.7, when trying to bound
![]() $f(n,k,d) = \min _s g(n,k,d;\;s)$
for large
$f(n,k,d) = \min _s g(n,k,d;\;s)$
for large
![]() $n$
, we can restrict our attention to
$n$
, we can restrict our attention to
![]() $s \in \{k-2,k-1\}$
. First we deal with the latter case.
$s \in \{k-2,k-1\}$
. First we deal with the latter case.
Lemma 3.9.
Let
![]() $n,k,d$
be positive integers such that
$n,k,d$
be positive integers such that
![]() $n \ge d \ge 1$
. Then
$n \ge d \ge 1$
. Then
Proof. To prove the statement, we will show that, for all positive integers
![]() $n,k,d$
with
$n,k,d$
with
![]() $n \ge d \ge 1$
, we have
$n \ge d \ge 1$
, we have
![]() $g(n+1,k,d;\;k-1) = g(n,k,d;\;k-1)+1$
. Combined with the simple observation that
$g(n+1,k,d;\;k-1) = g(n,k,d;\;k-1)+1$
. Combined with the simple observation that
![]() $g(d,k,d;\;k-1) =2^d k - 1$
for all
$g(d,k,d;\;k-1) =2^d k - 1$
for all
![]() $k \ge 1$
, since when
$k \ge 1$
, since when
![]() $d = n$
we are covering with individual points, this fact will indeed imply the desired result.
$d = n$
we are covering with individual points, this fact will indeed imply the desired result.
By Lemma 3.2 we know that
![]() $g(n+1,k,d;\;k-1) \geq g(n,k,d;\;k-1)+1$
. For the other inequality, consider an optimal
$g(n+1,k,d;\;k-1) \geq g(n,k,d;\;k-1)+1$
. For the other inequality, consider an optimal
![]() $(k,d;\;k-1)$
-cover
$(k,d;\;k-1)$
-cover
![]() $\mathcal{H}$
of
$\mathcal{H}$
of
![]() $\mathbb{F}_2^n$
. For every
$\mathbb{F}_2^n$
. For every
![]() $S\in \mathcal{H}$
, let
$S\in \mathcal{H}$
, let
![]() $S'=S\times \{0,1\}$
, which is a codimension-
$S'=S\times \{0,1\}$
, which is a codimension-
![]() $d$
affine subspace of
$d$
affine subspace of
![]() $\mathbb{F}_{2}^{n+1}$
, and let
$\mathbb{F}_{2}^{n+1}$
, and let
![]() $S_0$
be any
$S_0$
be any
![]() $(n + 1 - d)$
-dimensional affine subspace of
$(n + 1 - d)$
-dimensional affine subspace of
![]() $\mathbb{F}_{2}^{n+1}$
that contains the vector
$\mathbb{F}_{2}^{n+1}$
that contains the vector
![]() $(0,\ldots,0,1)$
but avoids the origin. We claim that
$(0,\ldots,0,1)$
but avoids the origin. We claim that
![]() $\mathcal{H}'=\{ S' \;:\; S\in \mathcal{H}\}\cup \{S_0\}$
is a
$\mathcal{H}'=\{ S' \;:\; S\in \mathcal{H}\}\cup \{S_0\}$
is a
![]() $(k,d;\;k-1)$
-cover of
$(k,d;\;k-1)$
-cover of
![]() $\mathbb{F}_{2}^{n+1}$
. Indeed, for all
$\mathbb{F}_{2}^{n+1}$
. Indeed, for all
![]() $S\in \mathcal{H}$
, a point of the form
$S\in \mathcal{H}$
, a point of the form
![]() $(\vec{x},t)$
is covered by
$(\vec{x},t)$
is covered by
![]() $S'$
if and only if
$S'$
if and only if
![]() $\vec{x}$
is covered by
$\vec{x}$
is covered by
![]() $S$
. Hence, the collection
$S$
. Hence, the collection
![]() $\{S' \;:\; S\in \mathcal{H}\}$
covers
$\{S' \;:\; S\in \mathcal{H}\}$
covers
![]() $\vec{0}$
exactly
$\vec{0}$
exactly
![]() $k-1$
times and each point of the form
$k-1$
times and each point of the form
![]() $(\vec{x},t)$
with
$(\vec{x},t)$
with
![]() $\vec{x} \neq \vec{0}$
at least
$\vec{x} \neq \vec{0}$
at least
![]() $k$
times. Finally, the point
$k$
times. Finally, the point
![]() $(\vec{0},1)$
is covered
$(\vec{0},1)$
is covered
![]() $k-1$
times by the
$k-1$
times by the
![]() $\{S' \;:\; S\in \mathcal{H}\}$
and once by the subspace
$\{S' \;:\; S\in \mathcal{H}\}$
and once by the subspace
![]() $S_0$
, so it is also covered the correct number of times. Hence
$S_0$
, so it is also covered the correct number of times. Hence
![]() $\mathcal{H}'$
is indeed a
$\mathcal{H}'$
is indeed a
![]() $(k,d;\;k-1)$
-cover of size
$(k,d;\;k-1)$
-cover of size
![]() $|\mathcal{H}|+1$
, and so the second inequality follows.
$|\mathcal{H}|+1$
, and so the second inequality follows.
Remark 3.10. Recall that the special case of
![]() $d = 1$
,
$d = 1$
,
![]() $g(n, k, 1;\; k - 1) = n + 2k - 2$
, also follows from [[Reference Sauermann and Wigderson24], Theorem 1.5].
$g(n, k, 1;\; k - 1) = n + 2k - 2$
, also follows from [[Reference Sauermann and Wigderson24], Theorem 1.5].
The proof of Theorem 1.2(b) is now straightforward.
Proof of Theorem
1.2(b). The upper bound is given by Lemma 3.1. For the lower bound, first observe that for any valid choice of the parameters, we have
![]() $g(n,k,d;\;s+1)\leq g(n,k,d;\;s)+1$
, as adding any subspace containing the origin to a
$g(n,k,d;\;s+1)\leq g(n,k,d;\;s)+1$
, as adding any subspace containing the origin to a
![]() $(k,d;\;s)$
-cover yields a
$(k,d;\;s)$
-cover yields a
![]() $(k,d;\;s+1)$
-cover. Then, by Corollary 3.7 and Lemma 3.9, we obtain
$(k,d;\;s+1)$
-cover. Then, by Corollary 3.7 and Lemma 3.9, we obtain
as desired.
4. Concluding remarks
In this paper, we investigated the minimum number of affine subspaces of a fixed codimension needed to cover all nonzero points of
![]() $\mathbb{F}_{2}^{n}$
at least
$\mathbb{F}_{2}^{n}$
at least
![]() $k$
times, while only covering the origin at most
$k$
times, while only covering the origin at most
![]() $k-1$
times. We were able to determine the answer precisely when
$k-1$
times. We were able to determine the answer precisely when
![]() $k$
is exponentially large with respect to
$k$
is exponentially large with respect to
![]() $n$
, or when
$n$
, or when
![]() $n$
is exponentially large with respect to
$n$
is exponentially large with respect to
![]() $k$
, and provided asymptotically sharp bounds for the range in between these extremes. In this final section, we highlight some open problems and avenues for further research.
$k$
, and provided asymptotically sharp bounds for the range in between these extremes. In this final section, we highlight some open problems and avenues for further research.
Tightness of the general upper bound
As remarked upon in the introduction, we know that the bound on
![]() $k$
in part (a) of our main result is best possible. However, as we explain below, for part (b) we believe the upper bound of Lemma 3.1 should be tight for much smaller values of
$k$
in part (a) of our main result is best possible. However, as we explain below, for part (b) we believe the upper bound of Lemma 3.1 should be tight for much smaller values of
![]() $n$
as well. For a more detailed discussion, we refer the reader to the arXiv version of this paper.
$n$
as well. For a more detailed discussion, we refer the reader to the arXiv version of this paper.
As we saw in Lemma 2.2, for our upper bounds we can generally reduce to the hyperplane setting, and so we shall focus on the
![]() $d=1$
case here. In this hyperplane setting, the upper bound of Lemma 3.1, valid for all
$d=1$
case here. In this hyperplane setting, the upper bound of Lemma 3.1, valid for all
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $k \ge 2$
, has the simple form
$k \ge 2$
, has the simple form
![]() $n + 2k - 3$
. Using the recursive bound in Lemma 3.2, we observe that if
$n + 2k - 3$
. Using the recursive bound in Lemma 3.2, we observe that if
![]() $f(n_0,k,1) = n_0 + 2k - 3$
for some positive integer
$f(n_0,k,1) = n_0 + 2k - 3$
for some positive integer
![]() $n_0$
, then
$n_0$
, then
![]() $f(n,k,1) = n + 2k - 3$
for all
$f(n,k,1) = n + 2k - 3$
for all
![]() $n\geq n_0$
. Hence, for every
$n\geq n_0$
. Hence, for every
![]() $k$
, there is a well-defined threshold
$k$
, there is a well-defined threshold
![]() $n_0(k)$
such that
$n_0(k)$
such that
![]() $f(n,k,1) = n + 2k - 3$
if and only if
$f(n,k,1) = n + 2k - 3$
if and only if
![]() $n \ge n_0(k)$
. Theorem 1.2(b) shows
$n \ge n_0(k)$
. Theorem 1.2(b) shows
![]() $n_0(k) \le 2^k + 1$
, while part (a) implies that
$n_0(k) \le 2^k + 1$
, while part (a) implies that
![]() $n_0(k) \gt \log _2 k + 2$
.
$n_0(k) \gt \log _2 k + 2$
.
We can obtain a linear lower bound on
![]() $n_0(k)$
for
$n_0(k)$
for
![]() $k\geq 4$
by considering the collection of hyperplanes in
$k\geq 4$
by considering the collection of hyperplanes in
![]() $\mathbb{F}_{2}^{k}$
containing
$\mathbb{F}_{2}^{k}$
containing
![]() $ H_{\vec{e}_i}$
and
$ H_{\vec{e}_i}$
and
![]() $H_{\vec{1}-\vec{e}_i}$
for each
$H_{\vec{1}-\vec{e}_i}$
for each
![]() $i\in [k]$
, where
$i\in [k]$
, where
![]() $\vec{e}_i$
denotes the
$\vec{e}_i$
denotes the
![]() $i$
th standard basis vector and
$i$
th standard basis vector and
![]() $\vec{1}$
the all-one vector, together with
$\vec{1}$
the all-one vector, together with
![]() $k-4$
copies of the hyperplane
$k-4$
copies of the hyperplane
![]() $\vec{x}\cdot \vec{1}=0$
. This collection has size
$\vec{x}\cdot \vec{1}=0$
. This collection has size
![]() $3k-4$
and one can check that it forms a
$3k-4$
and one can check that it forms a
![]() $k$
-cover of
$k$
-cover of
![]() $\mathbb{F}_{2}^{k}$
, implying that
$\mathbb{F}_{2}^{k}$
, implying that
![]() $n_0(k)\geq k+1$
, and this is the best general construction we have that improves the simple
$n_0(k)\geq k+1$
, and this is the best general construction we have that improves the simple
![]() $n + 2k -3$
bound. Indeed, while the extended binary Golay code, coupled with Proposition 3.3, shows that you can do better for
$n + 2k -3$
bound. Indeed, while the extended binary Golay code, coupled with Proposition 3.3, shows that you can do better for
![]() $8 \le k \le 11$
, this is known to be a very efficient, but sporadic, code, and we cannot generalise the construction to larger
$8 \le k \le 11$
, this is known to be a very efficient, but sporadic, code, and we cannot generalise the construction to larger
![]() $k$
. This leads us to ask the following question.
$k$
. This leads us to ask the following question.
Question 4.1.
Do we have
![]() $n_0(k) = k+1$
when
$n_0(k) = k+1$
when
![]() $k \ge 12$
?
$k \ge 12$
?
Equivalently, we are asking whether
![]() $3k-2$
hyperplanes are needed in a
$3k-2$
hyperplanes are needed in a
![]() $(k,1)$
-cover of
$(k,1)$
-cover of
![]() $\mathbb{F}_{2}^{k+1}$
. We observe that, exploiting the coding connection once again, the Gilbert–Varshamov bound, discussed in Remark 3.6, shows that a random collection of
$\mathbb{F}_{2}^{k+1}$
. We observe that, exploiting the coding connection once again, the Gilbert–Varshamov bound, discussed in Remark 3.6, shows that a random collection of
![]() $k+O(\log _2 k)$
hyperplanes forms a (3,1;0)-cover of
$k+O(\log _2 k)$
hyperplanes forms a (3,1;0)-cover of
![]() $\mathbb{F}_{2}^{k+1}$
with high probability. Adding
$\mathbb{F}_{2}^{k+1}$
with high probability. Adding
![]() $k-3$
pairs of parallel planes then yields a
$k-3$
pairs of parallel planes then yields a
![]() $(k,1)$
-cover of size
$(k,1)$
-cover of size
![]() $3k + O(\log _2 k)$
, showing that there are numerous asymptotically optimal covers. Hence, we cannot hope for any strong stability when
$3k + O(\log _2 k)$
, showing that there are numerous asymptotically optimal covers. Hence, we cannot hope for any strong stability when
![]() $n$
is comparable to
$n$
is comparable to
![]() $k$
, which could make the resolution of this question difficult, but as a first step one could attempt to reduce the exponential upper bound on
$k$
, which could make the resolution of this question difficult, but as a first step one could attempt to reduce the exponential upper bound on
![]() $n_0(k)$
. Furthermore, while we have focused on the hyperplane case in Question 4.1, it would also be worth exploring the corresponding threshold
$n_0(k)$
. Furthermore, while we have focused on the hyperplane case in Question 4.1, it would also be worth exploring the corresponding threshold
![]() $n_0(k,d)$
for
$n_0(k,d)$
for
![]() $d \ge 2$
, as it would be very interesting if there were new constructions that appear when covering with affine subspaces of codimension
$d \ge 2$
, as it would be very interesting if there were new constructions that appear when covering with affine subspaces of codimension
![]() $d$
.
$d$
.
Larger fields
In this paper we have worked exclusively over the binary field
![]() $\mathbb{F}_{2}^{}$
, but it is also natural to explore these subspace covering problems over larger finite fields,
$\mathbb{F}_{2}^{}$
, but it is also natural to explore these subspace covering problems over larger finite fields,
![]() $\mathbb{F}_q$
for
$\mathbb{F}_q$
for
![]() $q \gt 2$
. Let us denote the corresponding extremal function by
$q \gt 2$
. Let us denote the corresponding extremal function by
![]() $f_q(n, k, d)$
, which is the minimum cardinality of a multiset of
$f_q(n, k, d)$
, which is the minimum cardinality of a multiset of
![]() $(n - d)$
-dimensional affine subspaces that cover all points of
$(n - d)$
-dimensional affine subspaces that cover all points of
![]() $\mathbb{F}_q^n \setminus \{\vec{0}\}$
at least
$\mathbb{F}_q^n \setminus \{\vec{0}\}$
at least
![]() $k$
times, and the origin at most
$k$
times, and the origin at most
![]() $k - 1$
times. The work of Jamison [Reference Jamison16] establishes the initial values of this function, showing
$k - 1$
times. The work of Jamison [Reference Jamison16] establishes the initial values of this function, showing
![]() $f_q(n, 1, d) = (q - 1)(n - d) + q^d - 1$
. When it comes to multiplicities
$f_q(n, 1, d) = (q - 1)(n - d) + q^d - 1$
. When it comes to multiplicities
![]() $k \ge 2$
, some of what we have done here can be transferred to larger fields as well.
$k \ge 2$
, some of what we have done here can be transferred to larger fields as well.
To start, we can once again resolve the setting where the multiplicity
![]() $k$
is large with respect to the dimension
$k$
is large with respect to the dimension
![]() $n$
. Indeed, the double-counting lower bound of Lemma 2.1 generalises immediately to this setting, giving
$n$
. Indeed, the double-counting lower bound of Lemma 2.1 generalises immediately to this setting, giving
![]() $f_q(n, k, d) \geq q^d k - \left\lfloor{ \frac{k}{q^{n - d}} }\right\rfloor$
, and one can obtain a matching upper bound by taking multiple copies of every affine subspace.
$f_q(n, k, d) \geq q^d k - \left\lfloor{ \frac{k}{q^{n - d}} }\right\rfloor$
, and one can obtain a matching upper bound by taking multiple copies of every affine subspace.
In the other extreme, where
![]() $n$
is large with respect to
$n$
is large with respect to
![]() $k$
, the problem remains wide open. We first note that the reduction to hyperplanes from Lemma 2.2 can be extended, giving
$k$
, the problem remains wide open. We first note that the reduction to hyperplanes from Lemma 2.2 can be extended, giving
![]() $f_q(n, k, d) \leq f_q( n - d + 1, k, 1) + (q^{d - 1} - 1)kq$
. Thus, as before, it is best to first focus on the case
$f_q(n, k, d) \leq f_q( n - d + 1, k, 1) + (q^{d - 1} - 1)kq$
. Thus, as before, it is best to first focus on the case
![]() $d = 1$
, where Jamison’s result gives
$d = 1$
, where Jamison’s result gives
![]() $f_q(n, 1, 1) = (q - 1)n$
.
$f_q(n, 1, 1) = (q - 1)n$
.
For an upper bound, let us start by considering
![]() $2$
-covers. It is once again true that if one takes the standard
$2$
-covers. It is once again true that if one takes the standard
![]() $1$
-covering by hyperplanes, consisting of all hyperplanes of the form
$1$
-covering by hyperplanes, consisting of all hyperplanes of the form
![]() $\{\vec{x}\;:\; x_i = c \}$
for some
$\{\vec{x}\;:\; x_i = c \}$
for some
![]() $i \in [n]$
and
$i \in [n]$
and
![]() $c \in{\mathbb{F}_{q}^{}} \setminus \{0\}$
, the only nonzero vectors that are only covered once are those of Hamming weight
$c \in{\mathbb{F}_{q}^{}} \setminus \{0\}$
, the only nonzero vectors that are only covered once are those of Hamming weight
![]() $1$
. However, since the nonzero coordinate of these vectors can take any of
$1$
. However, since the nonzero coordinate of these vectors can take any of
![]() $q-1$
different values, it takes a further
$q-1$
different values, it takes a further
![]() $q-1$
hyperplanes to cover these again, and so we have
$q-1$
hyperplanes to cover these again, and so we have
![]() $f_q(n,2,1) \le (q-1)(n+1)$
. Now, given a
$f_q(n,2,1) \le (q-1)(n+1)$
. Now, given a
![]() $(k-1)$
-cover of
$(k-1)$
-cover of
![]() $\mathbb{F}_{q}^{n}$
, one can obtain a
$\mathbb{F}_{q}^{n}$
, one can obtain a
![]() $k$
-cover by adding an arbitrary partition of
$k$
-cover by adding an arbitrary partition of
![]() $\mathbb{F}_{q}^{n}$
into
$\mathbb{F}_{q}^{n}$
into
![]() $q$
parallel planes, and this yields
$q$
parallel planes, and this yields
![]() $f_q(n,k) \le (q-1)(n+1) + q(k-2)$
. This construction is the direct analogue of that from Lemma 3.1, and so, as in Theorem 1.2(b), we expect it to be tight when
$f_q(n,k) \le (q-1)(n+1) + q(k-2)$
. This construction is the direct analogue of that from Lemma 3.1, and so, as in Theorem 1.2(b), we expect it to be tight when
![]() $n$
is sufficiently large.
$n$
is sufficiently large.
Question 4.2.
For
![]() $n \ge n_0(k,q)$
, do we have
$n \ge n_0(k,q)$
, do we have
![]() $f_q(n,k,1) = (q-1)(n+1) + q(k-2)$
?
$f_q(n,k,1) = (q-1)(n+1) + q(k-2)$
?
As we already have the construction above, one needs to prove a matching lower bound. It would of course be very helpful to use some of the machinery we have developed here, and so we briefly explain where the difficulties therein lie. Key to our binary proof was the equivalence with codes of a certain minimum weight, but this breaks down over
![]() $\mathbb{F}_{q}^{}$
. While we can show that every
$\mathbb{F}_{q}^{}$
. While we can show that every
![]() $(k,1)$
-covering of
$(k,1)$
-covering of
![]() $\mathbb{F}_{q}^{n}$
gives rise to a linear
$\mathbb{F}_{q}^{n}$
gives rise to a linear
![]() $q$
-ary
$q$
-ary
![]() $n$
-dimensional code of minimum distance at least
$n$
-dimensional code of minimum distance at least
![]() $k(q-1)$
, the converse is not true. As a result, the coding theoretic bounds, which are of the form
$k(q-1)$
, the converse is not true. As a result, the coding theoretic bounds, which are of the form
![]() $n + O(k q \log _q n)$
, are not strong enough to give us information here.
$n + O(k q \log _q n)$
, are not strong enough to give us information here.
Another main tool was the recursion over
![]() $n$
, showing that
$n$
, showing that
![]() $f(n,k,1)$
is strictly increasing in
$f(n,k,1)$
is strictly increasing in
![]() $n$
. The same proof goes through here, and we can again show
$n$
. The same proof goes through here, and we can again show
![]() $f_q(n,k,1) \gt f_q(n-1,k,1)$
. However, from our bounds, we expect the stronger inequality
$f_q(n,k,1) \gt f_q(n-1,k,1)$
. However, from our bounds, we expect the stronger inequality
![]() $f_q(n,k,1) \ge f_q(n-1,k,1) + q - 1$
to hold. Intuitively, this is because when we restrict a
$f_q(n,k,1) \ge f_q(n-1,k,1) + q - 1$
to hold. Intuitively, this is because when we restrict a
![]() $k$
-cover of
$k$
-cover of
![]() $\mathbb{F}_{q}^{n}$
to
$\mathbb{F}_{q}^{n}$
to
![]() ${\mathbb{F}_{q-1}^{n}} \subseteq{\mathbb{F}_{q}^{n}}$
, there are
${\mathbb{F}_{q-1}^{n}} \subseteq{\mathbb{F}_{q}^{n}}$
, there are
![]() $q-1$
affine copies of
$q-1$
affine copies of
![]() $\mathbb{F}_{q-1}^{n}$
that are lost. However, this does not (appear to) come out of our probabilistic argument.
$\mathbb{F}_{q-1}^{n}$
that are lost. However, this does not (appear to) come out of our probabilistic argument.
A simple general lower bound is obtained by noticing that removing
![]() $k-1$
hyperplanes from a
$k-1$
hyperplanes from a
![]() $(k,1)$
-cover leaves us with at least a
$(k,1)$
-cover leaves us with at least a
![]() $(1,1)$
-cover, and so
$(1,1)$
-cover, and so
![]() . This remains the best lower bound we know—in particular, even the case of
. This remains the best lower bound we know—in particular, even the case of
![]() $f_q(n,2,1)$
is unsolved. It would thus be of great interest to develop new tools to handle the
$f_q(n,2,1)$
is unsolved. It would thus be of great interest to develop new tools to handle the
![]() $q$
-ary case, as these may also bear fruit when applied to the open problems in the binary setting, and we believe that new algebraic ideas may be useful here.
$q$
-ary case, as these may also bear fruit when applied to the open problems in the binary setting, and we believe that new algebraic ideas may be useful here.
Polynomials with large multiplicity
Finally, speaking of algebraic methods, we return to our introductory discussion of the polynomial method. Recall that previous lower bounds in this area have been obtained by considering the more general problem of the minimum degree of a polynomial in
![]() ${\mathbb{F}_{}^{}}[x_1, x_2, \ldots, x_n]$
that vanishes with multiplicity at least
${\mathbb{F}_{}^{}}[x_1, x_2, \ldots, x_n]$
that vanishes with multiplicity at least
![]() $k$
at all nonzero points in some finite grid, and with lower multiplicity at the origin. Sauermann and Wigderson’s recent breakthrough, Theorem 1.1, resolves this polynomial problem for
$k$
at all nonzero points in some finite grid, and with lower multiplicity at the origin. Sauermann and Wigderson’s recent breakthrough, Theorem 1.1, resolves this polynomial problem for
![]() $n \ge 2k-3$
over fields of characteristic 0, while our results here show that, in the binary setting at least, there is separation between the hyperplane covering and the polynomial problems.
$n \ge 2k-3$
over fields of characteristic 0, while our results here show that, in the binary setting at least, there is separation between the hyperplane covering and the polynomial problems.
Despite this, we wonder whether the answers to the two problems might coincide in the range where the multiplicity
![]() $k$
is large with respect to the dimension
$k$
is large with respect to the dimension
![]() $n$
. That is, can the simple double-counting hyperplane lower bound be strengthened to the polynomial setting? We would therefore like to close by emphasising a question of Sauermann and Wigderson [Reference Sauermann and Wigderson24], this time over
$n$
. That is, can the simple double-counting hyperplane lower bound be strengthened to the polynomial setting? We would therefore like to close by emphasising a question of Sauermann and Wigderson [Reference Sauermann and Wigderson24], this time over
![]() $\mathbb{F}_{2}^{}$
.
$\mathbb{F}_{2}^{}$
.
Question 4.3.
Given positive integers
![]() $k, n$
with
$k, n$
with
![]() $k \ge 2^{n-2}$
, let
$k \ge 2^{n-2}$
, let
![]() $P \in{\mathbb{F}_{2}^{}}[x_1, x_2, \ldots, x_n]$
be a polynomial that vanishes with multiplicity at least
$P \in{\mathbb{F}_{2}^{}}[x_1, x_2, \ldots, x_n]$
be a polynomial that vanishes with multiplicity at least
![]() $k$
at every nonzero point, and with multiplicity at most
$k$
at every nonzero point, and with multiplicity at most
![]() $k-1$
at the origin. Must we then have
$k-1$
at the origin. Must we then have
![]() $\deg\!(P) \ge 2k - \left\lfloor{\frac{k}{2^{n-1}}}\right\rfloor$
?
$\deg\!(P) \ge 2k - \left\lfloor{\frac{k}{2^{n-1}}}\right\rfloor$
?
Acknowledgements
This work was carried out when the authors were all working at the Institut für Mathematik of the Freie Universität Berlin, and we would like to thank the Combinatorics and Graph Theory research group for providing a fertile and enjoyable working environment. We are also grateful to the anonymous referees for their helpful suggestions.