Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-20T12:25:14.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Spread-out limit of the critical points for lattice trees and lattice animals in dimensions 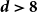$\boldsymbol{d}\boldsymbol\gt \textbf{8}$

Part of: Equilibrium statistical mechanics Special processes

Published online by Cambridge University Press:  20 November 2023

Noe Kawamoto Open the ORCID record for Noe Kawamoto [Opens in a new window]  and
Akira Sakai Open the ORCID record for Akira Sakai [Opens in a new window]
Noe Kawamoto*
Affiliation:
Graduate School of Science, Hokkaido University, Sapporo, Japan
Akira Sakai
Affiliation:
Faculty of Science, Hokkaido University, Sapporo, Japan
*
Corresponding author: Noe Kawamoto; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A spread-out lattice animal is a finite connected set of edges in 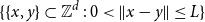$\{\{x,y\}\subset \mathbb{Z}^d\;:\;0\lt \|x-y\|\le L\}$. A lattice tree is a lattice animal with no loops. The best estimate on the critical point 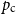$p_{\textrm{c}}$ so far was achieved by Penrose (J. Stat. Phys. 77, 3–15, 1994) : 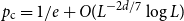$p_{\textrm{c}}=1/e+O(L^{-2d/7}\log L)$ for both models for all 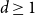$d\ge 1$. In this paper, we show that 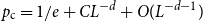$p_{\textrm{c}}=1/e+CL^{-d}+O(L^{-d-1})$ for all 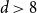$d\gt 8$, where the model-dependent constant 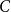$C$ has the random-walk representation

\begin{align*} C_{\textrm{LT}}=\sum _{n=2}^\infty \frac{n+1}{2e}U^{*n}(o),&& C_{\textrm{LA}}=C_{\textrm{LT}}-\frac 1{2e^2}\sum _{n=3}^\infty U^{*n}(o), \end{align*}
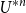where $U^{*n}$ is the $n$-fold convolution of the uniform distribution on the 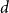$d$-dimensional ball 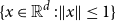$\{x\in{\mathbb R}^d\;: \|x\|\le 1\}$. The proof is based on a novel use of the lace expansion for the 2-point function and detailed analysis of the 1-point function at a certain value of 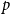$p$ that is designed to make the analysis extremely simple.

Keywords

Lattice treeslattice animalscritical phenomena

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82B27: Critical phenomena
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 2 , March 2024 , pp. 238 - 269
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Brydges, D. C., Helmuth, T. and Holmes, M. (2021) The continuous-time lace expansion. Commun. Pure Appl. Math. 74(11) 2251–2309.CrossRefGoogle Scholar
Brydges, D. C. and Spencer, T. (1985) Self-avoiding walk in 5 or more dimensions. Commun. Math. Phys. 97(1-2) 125–148.CrossRefGoogle Scholar
Chen, L.-C. and Sakai, A. (2008) Critical behavior and the limit distribution for long-range oriented percolation. I. Probab. Theory Relat. Fields 142(1-2) 151–188.CrossRefGoogle Scholar
Chen, L.-C. and Sakai, A. (2015) Critical two-point functions for long-range statistical-mechanical models in high dimensions. Ann. Probab. 43(2) 639–681.CrossRefGoogle Scholar
Fitzner, R. and van der Hofstad, R. (2021) NoBLE for lattice trees and lattice animals. J. Stat. Phys. 185(2) No.13.CrossRefGoogle Scholar
Hara, T., Hofstad, Rvd and Slade, G. (2003) Critical two-point functions and the lace expansion for spread-out high-dimensional percolation and related models. Ann. Probab. 31(1) 349–408.CrossRefGoogle Scholar
Hara, T. and Slade, G. (1990) Mean-field critical behaviour for percolation in high dimensions. Commun. Math. Phys. 128(2) 333–391.CrossRefGoogle Scholar
Hara, T. and Slade, G. (1990) On the upper critical dimension of lattice trees and lattice animals. J. Stat. Phys. 59(5-6) 1469–1510.CrossRefGoogle Scholar
Hara, T. and Slade, G. (1992) Self-avoiding walk in five or more dimensions I. The critical behaviour. Commun. Math. Phys. 147(1) 101–136.CrossRefGoogle Scholar
Hara, T. and Slade, G. (1992) The number and size of branched polymers in high dimensions. J. Stat. Phys. 67(5-6) 438–470.CrossRefGoogle Scholar
van der Hofstad, R. and Sakai, A. (2004) Gaussian scaling for the critical spread-out contact process above the upper critical dimension. Electron. J. Probab. 9 710–769.CrossRefGoogle Scholar
Hofstad, Rvd and Sakai, A. (2005) Critical points for spread-out self-avoiding walk, percolation and the contact process above the upper critical dimensions. Probab. Theory Relat. Fields 132(3) 438–470.CrossRefGoogle Scholar
van der Hofstad, R. and Sakai, A. (2010) Convergence of the critical finite-range contact process to super-Brownian motion above the upper critical dimension: the higher-point functions. Electron. J. Probab. 15 801–894.CrossRefGoogle Scholar
van der Hofstad, R. and Slade, G. (2002) A generalised inductive approach to the lace expansion. Probab. Theory Relat. Fields 122(3) 389–430.CrossRefGoogle Scholar
Klarner, D. A. (1967) Cell growth problems. Canad. J. Math. 19 851–863.CrossRefGoogle Scholar
Klein, D. J. (1981) Rigorous results for branched polymer models with excluded volume. J. Chem. Phys. 75(10) 5186–5189.CrossRefGoogle Scholar
Liang, Y. (2022) Critical point for spread-out lattice trees in dimensions $d\gt 8$. Master thesis, Hokkaido University.Google Scholar
Madras, N. and Slade, G. (1993) The Self-Avoiding Walk. Birkhäuser.Google Scholar
Miranda, Y. M. (2012) The critical points of lattice trees and lattice animals in high dimensions. Ph.D thesis, University of British Columbia.Google Scholar
Miranda, Y. M. and Slade, G. (2011) The growth constants of lattice trees and lattice animals in high dimensions. Electron. Commun. Probab. 16 129–136.Google Scholar
Miranda, Y. M. and Slade, G. (2013) Expansion in high dimension for the growth constants of lattice trees and lattice animals. Combin. Probab. Comput. 22(4) 527–565.CrossRefGoogle Scholar
Nguyen, B. G. and Yang, W.-S. (1993) Triangle condition for oriented percolation in high dimensions. Ann. Probab. 21(4) 1809–1844.CrossRefGoogle Scholar
Penrose, M. D. (1994) Self-avoiding walks and trees in spread-out lattices. J. Stat. Phys. 77(1-2) 3–15.CrossRefGoogle Scholar
Sakai, A. (2001) Mean-field critical behavior for the contact process. J. Stat. Phys. 104(1/2) 111–143.CrossRefGoogle Scholar
Sakai, A. (2007) Lace expansion for the Ising model. Commun. Math. Phys. 272(2) 283–344.CrossRefGoogle Scholar
Sakai, A. (2015) Application of the lace expansion to the $\varphi ^4$ model. Commun. Math. Phys. 336 619–648.CrossRefGoogle Scholar
Sakai, A. (2022) Correct bounds on the Ising lace-expansion coefficients. Commun. Math. Phys. 392(3) 783–823.CrossRefGoogle Scholar