Article contents
Spanning 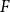 $F$-cycles in random graphs
$F$-cycles in random graphs
Published online by Cambridge University Press: 09 June 2023
Abstract
We extend a recent argument of Kahn, Narayanan and Park ((2021) Proceedings of the AMS 149 3201–3208) about the threshold for the appearance of the square of a Hamilton cycle to other spanning structures. In particular, for any spanning graph, we give a sufficient condition under which we may determine its threshold. As an application, we find the threshold for a set of cyclically ordered copies of 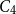 $C_4$ that span the entire vertex set, so that any two consecutive copies overlap in exactly one edge and all overlapping edges are disjoint. This answers a question of Frieze. We also determine the threshold for edge-overlapping spanning
$C_4$ that span the entire vertex set, so that any two consecutive copies overlap in exactly one edge and all overlapping edges are disjoint. This answers a question of Frieze. We also determine the threshold for edge-overlapping spanning 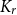 $K_r$-cycles.
$K_r$-cycles.
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by



