Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T17:13:03.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Size Ramsey Number of Bounded Degree Graphs for Games

Published online by Cambridge University Press:  11 June 2013

HEIDI GEBAUER
HEIDI GEBAUER*
Affiliation:
Institute of Theoretical Computer Science, ETH Zurich, CH-8092Switzerland (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study Maker/Breaker games on the edges of sparse graphs. Maker and Breaker take turns at claiming previously unclaimed edges of a given graph H. Maker aims to occupy a given target graph G and Breaker tries to prevent Maker from achieving his goal. We show that for every d there is a constant c = c(d) with the property that for every graph G on n vertices of maximum degree d there is a graph H on at most cn edges such that Maker has a strategy to occupy a copy of G in the game on H.

This is a result about a game-theoretic variant of the size Ramsey number. For a given graph G, 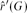$\hat{r}'(G)$ is defined as the smallest number M for which there exists a graph H with M edges such that Maker has a strategy to occupy a copy of G in the game on H. In this language, our result yields that for every connected graph G of constant maximum degree, 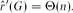$\hat{r}'(G) = \Theta(n)$.

Moreover, we can also use our method to settle the corresponding extremal number for universal graphs: for a constant d and for the class 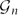${\cal G}_{n}$ of n-vertex graphs of maximum degree d, 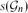$s({\cal G}_{n})$ denotes the minimum number such that there exists a graph H with M edges where, for everyG ∈ 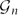${\cal G}_{n}$, Maker has a strategy to build a copy of G in the game on H. We obtain that 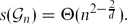$s({\cal G}_{n}) = \Theta(n^{2 - \frac{2}{d}})$.

Keywords

Primary 05C5505C5791A4391A46
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 4 , July 2013 , pp. 499 - 516
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Asodi, V. (2002) Sparse universal graphs. J. Comput. Appl. Math. 142 1–11.Google Scholar
[2]Alon, N. and Capalbo, M. (2007) Sparse universal graphs for bounded degree graphs. Random Struct. Alg. 31 123–133.Google Scholar
[3]Alon, N. and Capalbo, M. (2008) Optimal universal graphs with deterministic embedding. In Proc. 19th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA), pp. 373–378.Google Scholar
[4]Alon, N., Capalbo, M., Kohayakawa, Y., Rödl, V., Ruciński, A. and Szemerédi, E. (2000) Universality and tolerance. In Proc. 41st IEEE Symposium on Foundations of Computer Science (FOCS), pp. 14–21.Google Scholar
[5]Alon, N., Capalbo, M., Kohayakawa, Y., Rödl, V., Ruciński, A. and Szemerédi, E. (2001) Near-optimum universal graphs for graphs with bounded degrees. In RANDOM–APPROX, pp. 170–180.Google Scholar
[6]Alon, N., Krivelevich, M., Spencer, J. and Szabó, T. (2005) Discrepancy games. Electron. J. Combin. 12 R51.CrossRefGoogle Scholar
[7]Babai, L., Chung, F. R. K., Erdős, P., Graham, R. L. and Spencer, J. (1982) On graphs which contain all sparse graphs. Ann. Discrete Math. 12 21–26.Google Scholar
[8]Beck, J. (1981) Van der Waerden and Ramsey type games. Combinatorica 1 103–116.Google Scholar
[9]Beck, J. (1983) On size Ramsey number of paths, trees and cycles I. J. Graph Theory 7 115–130.Google Scholar
[10]Beck, J. (1994) Deterministic graph games and a probabilistic intuition. Combin. Probab. Comput. 3 13–26.Google Scholar
[11]Bhatt, S. N., Chung, F., Leighton, F. T. and Rosenberg, A. (1989) Universal graphs for bounded-degree trees and planar graphs. SIAM J. Discrete Math. 2 145–155.Google Scholar
[12]Bhatt, S. N. and Leiserson, C. E. (1984) How to assemble tree machines. In Advances in Computing Research 2, (Preparata, F. P., ed.) JAI Press, Greenwich, CT, pp. 95–114.Google Scholar
[13]Capalbo, M. (1999) A small universal graph for bounded-degree planar graphs. In Proc. 10th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA), pp. 150–154.Google Scholar
[14]Capalbo, M. and Kosaraju, S. R. (1999) Small universal graphs. In Proc. 31st Annual ACM Symposium on Theory of Computing (STOC), pp. 741–749.Google Scholar
[15]Chung, F. R. K. and Graham, R. L. (1978) On graphs which contain all small trees. J. Combin. Theory Ser. B 24 14–23.Google Scholar
[16]Chung, F. R. K. and Graham, R. L. (1979) On universal graphs. Ann. New York Acad. Sci. 319 136–140.Google Scholar
[17]Chung, F. R. K. and Graham, R. L. (1983) On universal graphs for spanning trees. Proc. London Math. Soc. 27 203–211.Google Scholar
[18]Chung, F. R. K., Rosenberg, A. L. and Snyder, L. (1983) Perfect storage representations for families of data structures. SIAM J. Alg. Discrete Methods 4 548–565.Google Scholar
[19]Chung, F. and Graham, R. (1998) Erdős on Graphs: His Legacy of Unsolved Problems, A. K. Peters.CrossRefGoogle Scholar
[20]Chvátal, V., Rödl, V., Szemerédi, E. and Trotter, W. T. (1983) The Ramsey number of a graph with bounded maximum degree. J. Combin. Theory Ser. B 34 239–243.Google Scholar
[21]Erdős, P., Faudree, R. J., Rousseau, C. C. and Schelp, R. H. (1978) The size Ramsey number. Period. Math. Hungar. 9 145–161.Google Scholar
[22]Feldheim, O. N. and Krivelevich, M. (2008) Winning fast in sparse graph construction games. Combin. Probab. Comput. 17 781–791.Google Scholar
[23]Fox, J. and Sudakov, B. (2009) Two remarks on the Burr–Erdőos conjecture. Europ. J. Combin. 30 1630–1645.Google Scholar
[24]Friedman, J. and Pippenger, N. (1987) Expanding graphs contain all small trees. Combinatorica 7 71–76.Google Scholar
[25]Haxell, P. E., Kohayakawa, Y. and Łuczak, T. (1995) The induced size-Ramsey number of cycles. Combin. Probab. Comput. 4 217–239.Google Scholar
[26]Kohayakawa, Y., Rödl, V., Schacht, M. and Szemerédi, E. (2011) Sparse partition universal graphs for graphs of bounded degree. Adv. Math. 226 5041–5065.Google Scholar
[27]Rödl, V. (1981) A note on universal graphs. Ars Combin. 11 225–229.Google Scholar
[28]Rödl, V. and Szemerédi, E. (2000) On size Ramsey numbers of graphs with bounded degree. Combinatorica 20 257–262.Google Scholar
[29]Székely, L. A. (1984) On two concepts of discrepancy in a class of combinatorial games. In Infinite and Finite Sets, Vol. 37 of Colloquia Mathematica Societatis Janos Bolyai, pp. 679–683.Google Scholar