Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Borodin, O.V.
Kostochka, A.V.
and
Woodall, D.R.
1997.
List Edge and List Total Colourings of Multigraphs.
Journal of Combinatorial Theory, Series B,
Vol. 71,
Issue. 2,
p.
184.
Hilton, A.J.W.
Stirling, D.S.G.
and
Slivnik, T.
1998.
A Vertex-Splitting Lemma, de Werra's Theorem, and Improper List Colourings.
Journal of Combinatorial Theory, Series B,
Vol. 72,
Issue. 1,
p.
91.
Juvan, Martin
Mohar, Bojan
and
??krekovski, Riste
1999.
Graphs of degree 4 are 5-edge-choosable.
Journal of Graph Theory,
Vol. 32,
Issue. 3,
p.
250.
Cropper, M. M.
and
Hilton, A. J. W.
2002.
Hall parameters of complete and complete bipartite graphs.
Journal of Graph Theory,
Vol. 41,
Issue. 3,
p.
208.
Cohen, Nathann
and
Havet, Frédéric
2010.
Planar graphs with maximum degree Δ≥9 are (Δ+1)-edge-choosable—A short proof.
Discrete Mathematics,
Vol. 310,
Issue. 21,
p.
3049.
Stones, Douglas S.
and
Wanless, Ian M.
2012.
Hownotto prove the Alon-Tarsi conjecture.
Nagoya Mathematical Journal,
Vol. 205,
Issue. ,
p.
1.
Stones, Douglas S.
and
Wanless, Ian M.
2012.
Hownotto prove the Alon-Tarsi conjecture.
Nagoya Mathematical Journal,
Vol. 205,
Issue. ,
p.
1.
Feder, Tomás
and
Subi, Carlos
2013.
Edge-coloring almost bipartite multigraphs.
Information Processing Letters,
Vol. 113,
Issue. 18,
p.
685.
van Bevern, René
and
Pyatkin, Artem V.
2016.
Computer Science – Theory and Applications.
Vol. 9691,
Issue. ,
p.
73.
Gera, Ralucca
Haynes, Teresa W.
Hedetniemi, Stephen T.
and
Henning, Michael A.
2018.
Graph Theory.
p.
177.


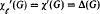 . Here we give a brief self-contained proof of this result.
. Here we give a brief self-contained proof of this result.