Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-20T05:52:08.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp bounds for a discrete John’s theorem

Part of: Discrete geometry General convexity

Published online by Cambridge University Press:  05 March 2024

Peter van Hintum Open the ORCID record for Peter van Hintum [Opens in a new window]  and
Peter Keevash Open the ORCID record for Peter Keevash [Opens in a new window]
Peter van Hintum*
Affiliation:
New College, University of Oxford, Oxford, UK
Peter Keevash
Affiliation:
Mathematical Institute, University of Oxford, Oxford, UK
*
Corresponding author: Peter van Hintum; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Tao and Vu showed that every centrally symmetric convex progression 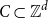$C\subset \mathbb{Z}^d$ is contained in a generalized arithmetic progression of size 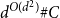$d^{O(d^2)} \# C$. Berg and Henk improved the size bound to 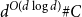$d^{O(d\log d)} \# C$. We obtain the bound 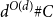$d^{O(d)} \# C$, which is sharp up to the implied constant and is of the same form as the bound in the continuous setting given by John’s theorem.

Keywords

Convex progressiongeneralised arithmetic progressionJohn’s theorem

MSC classification

Primary: 52C07: Lattices and convex bodies in $n$ dimensions
Secondary: 52A27: Approximation by convex sets
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 4 , July 2024 , pp. 484 - 486
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berg, S. L. and Henk, M. (2019) Discrete analogues of John’s theorem. Moscow J. Comb. Number Theory 8(4) 367–378.CrossRefGoogle Scholar
John, F. (1948) Extremum problems with inequalities as subsidiary conditions. In Studies and Essays, Presented to R. Courant on his 60th Birthday,. New York: Interscience, pp. 187–204.Google Scholar
Lovett, S. and Regev, O. (2017) A counterexample to a strong variant of the Polynomial Freiman-Ruzsa Conjecture in Euclidean space. Discrete Anal. 8 379–388.Google Scholar
Tao, T. and Vu, V. (2006) Additive Combinatorics. Cambridge University Press, Vol. 105.CrossRefGoogle Scholar
Tao, T. and Van, V. (2008) John-type theorems for generalized arithmetic progressions and iterated sumsets. Adv. Math. 219(2) 428–449.CrossRefGoogle Scholar