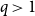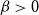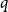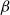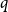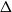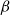1. Introduction
Glauber dynamics is a well-studied Markov chain that is widely used to sample from spin systems such as the Ising and Potts models. A particularly appealing feature of the chain is that it is usually very simple to implement; yet, establishing whether convergence to the equilibrium distribution is fast turns out to be significantly harder, and typically requires an in-depth understanding of the underlying distribution. Here, we focus on studying the performance of Glauber dynamics for the random cluster representation of the classical Potts model on the random regular graph, where the behaviour of the chain is underpinned by various phenomena that distinguish it from classical spin systems and pose new challenges in the analysis.
We begin with a few definitions. For real numbers
![]() $q, \beta \gt 0$
and a graph
$q, \beta \gt 0$
and a graph
![]() $G = (V,E)$
, the random cluster model on
$G = (V,E)$
, the random cluster model on
![]() $G$
with parameters
$G$
with parameters
![]() $q$
and
$q$
and
![]() $\beta$
is a probability distribution on the set
$\beta$
is a probability distribution on the set
![]() $\Omega =\Omega _G$
of all assignments
$\Omega =\Omega _G$
of all assignments
![]() ${\mathcal{F}}\;:\;E\rightarrow \{0,1\}$
; we typically refer to assignments in
${\mathcal{F}}\;:\;E\rightarrow \{0,1\}$
; we typically refer to assignments in
![]() $\Omega$
as configurations. For a configuration
$\Omega$
as configurations. For a configuration
![]() $\mathcal{F}$
, we say that edges mapped to
$\mathcal{F}$
, we say that edges mapped to
![]() $1$
are in-edges, and edges mapped to
$1$
are in-edges, and edges mapped to
![]() $0$
are out-edges. We use
$0$
are out-edges. We use
![]() ${\mathrm{In}}({\mathcal{F}})$
to denote the set of edges
${\mathrm{In}}({\mathcal{F}})$
to denote the set of edges
![]() $e$
with
$e$
with
![]() ${\mathcal{F}}(e)=1$
,
${\mathcal{F}}(e)=1$
,
![]() $\mathrm{Out}({\mathcal{F}})$
to denote the set of edges
$\mathrm{Out}({\mathcal{F}})$
to denote the set of edges
![]() $e$
with
$e$
with
![]() ${\mathcal{F}}(e)=0$
,
${\mathcal{F}}(e)=0$
,
![]() $|{\mathcal{F}}|$
for the cardinality of
$|{\mathcal{F}}|$
for the cardinality of
![]() ${\mathrm{In}}({\mathcal{F}})$
and
${\mathrm{In}}({\mathcal{F}})$
and
![]() $c({\mathcal{F}})$
for the number of connected components in the graph
$c({\mathcal{F}})$
for the number of connected components in the graph
![]() $(V,{\mathrm{In}}({\mathcal{F}}))$
. Then, the weight of
$(V,{\mathrm{In}}({\mathcal{F}}))$
. Then, the weight of
![]() $\mathcal{F}$
in the RC model is given by
$\mathcal{F}$
in the RC model is given by
![]() $w_G({\mathcal{F}})= q^{c({\mathcal{F}})} (e^\beta -1)^{|{\mathcal{F}}|}$
.
$w_G({\mathcal{F}})= q^{c({\mathcal{F}})} (e^\beta -1)^{|{\mathcal{F}}|}$
.
For integer values of
![]() $q$
, the RC model is closely connected to the (ferromagnetic) Ising/Potts models;
$q$
, the RC model is closely connected to the (ferromagnetic) Ising/Potts models;
![]() $q=2$
is the Ising model and
$q=2$
is the Ising model and
![]() $q\geq 3$
is the Potts model whose configurations are all possible assignments of
$q\geq 3$
is the Potts model whose configurations are all possible assignments of
![]() $q$
colours to the vertices of the graph where an assignment
$q$
colours to the vertices of the graph where an assignment
![]() $\sigma$
has weight proportional to
$\sigma$
has weight proportional to
![]() $\mathrm{e}^{\beta m(\sigma )}$
with
$\mathrm{e}^{\beta m(\sigma )}$
with
![]() $m(\sigma )$
being the number of monochromatic edges under
$m(\sigma )$
being the number of monochromatic edges under
![]() $\sigma$
. The RC model is an alternative edge representation of the models (for integer
$\sigma$
. The RC model is an alternative edge representation of the models (for integer
![]() $q$
) that has also been studied extensively in its own right due to its intricate behaviour (see, e.g., [Reference Grimmett18]).
$q$
) that has also been studied extensively in its own right due to its intricate behaviour (see, e.g., [Reference Grimmett18]).
We will be primarily interested in sampling from the so-called Gibbs distribution on
![]() $\Omega$
induced by these weights, denoted by
$\Omega$
induced by these weights, denoted by
![]() $\pi _G(\cdot )$
, where for a configuration
$\pi _G(\cdot )$
, where for a configuration
![]() $\mathcal{F}$
,
$\mathcal{F}$
,
![]() $\pi _G({\mathcal{F}}) =w_G({\mathcal{F}})/Z_G$
where the normalising factor
$\pi _G({\mathcal{F}}) =w_G({\mathcal{F}})/Z_G$
where the normalising factor
![]() $Z_G = \sum _{{\mathcal{F}}'\in \Omega _G}w_G({\mathcal{F}}')$
is the aggregate sum of weight of all configurations (known as the partition function). We focus on the Glauber dynamics which is a classical Markov chain for sampling from Gibbs distributions which is a particularly useful tool for developing approximate sampling algorithms. We will refer to Glauber dynamics for the RC model as the RC dynamics. Roughly, the RC dynamics is a Markov chain
$Z_G = \sum _{{\mathcal{F}}'\in \Omega _G}w_G({\mathcal{F}}')$
is the aggregate sum of weight of all configurations (known as the partition function). We focus on the Glauber dynamics which is a classical Markov chain for sampling from Gibbs distributions which is a particularly useful tool for developing approximate sampling algorithms. We will refer to Glauber dynamics for the RC model as the RC dynamics. Roughly, the RC dynamics is a Markov chain
![]() $(X_t)_{t\geq 0}$
initialised at some configuration
$(X_t)_{t\geq 0}$
initialised at some configuration
![]() $X_0$
which evolves by iteratively updating at each step
$X_0$
which evolves by iteratively updating at each step
![]() $t\geq 1$
a randomly chosen edge based on whether its endpoints belong to the same component in the graph
$t\geq 1$
a randomly chosen edge based on whether its endpoints belong to the same component in the graph
![]() $(V,{\mathrm{In}}(X_t))$
. The mixing time of the chain is the number of steps to get within total variation distance
$(V,{\mathrm{In}}(X_t))$
. The mixing time of the chain is the number of steps to get within total variation distance
![]() $\leq 1/4$
from
$\leq 1/4$
from
![]() $\pi _G$
, see Section 2 for details.
$\pi _G$
, see Section 2 for details.
Our goal is to obtain a fast algorithm for the RC model using Glauber dynamics on the random regular graph. There are two key obstacles that arise, especially at low temperatures (large
![]() $\beta$
): (i) Glauber dynamics for the RC model has a non-local behaviour since its updates depend on the component structure of the running configuration, and (ii) there are severe bottleneck phenomena and worst-case graphs which prohibit a general fast-convergence result, and more generally an efficient algorithm. The random regular graph is a particularly interesting testbed in this front since it exhibits all the relevant phase transition phenomena and has also been used as the main gadget in hardness reductions [Reference Galanis, Štefankovic, Vigoda and Yang14].
$\beta$
): (i) Glauber dynamics for the RC model has a non-local behaviour since its updates depend on the component structure of the running configuration, and (ii) there are severe bottleneck phenomena and worst-case graphs which prohibit a general fast-convergence result, and more generally an efficient algorithm. The random regular graph is a particularly interesting testbed in this front since it exhibits all the relevant phase transition phenomena and has also been used as the main gadget in hardness reductions [Reference Galanis, Štefankovic, Vigoda and Yang14].
To overview the phenomena that are most relevant for us, the following picture was detailed in a remarkable development by Jenssen, Helmuth, and Perkins [Reference Helmuth, Jenssen and Perkins21]: for
![]() $\Delta \geq 5$
and all sufficiently large
$\Delta \geq 5$
and all sufficiently large
![]() $q$
, they established the ordered/disordered transition occurring at some
$q$
, they established the ordered/disordered transition occurring at some
![]() $\beta _c$
satisfying
$\beta _c$
satisfying
![]() $\beta _c=(1+o_q(1))\tfrac{2\log q}{\Delta }$
(see also [Reference Galanis, Štefankovic, Vigoda and Yang14] for integer
$\beta _c=(1+o_q(1))\tfrac{2\log q}{\Delta }$
(see also [Reference Galanis, Štefankovic, Vigoda and Yang14] for integer
![]() $q\geq 3$
).Footnote
1
Roughly, for
$q\geq 3$
).Footnote
1
Roughly, for
![]() $\beta \lt \beta _c$
a typical configuration of the model is disordered, whereas for
$\beta \lt \beta _c$
a typical configuration of the model is disordered, whereas for
![]() $\beta \gt \beta _c$
it is ordered: disordered configurations resemble the all-out configuration (in that all components are of size
$\beta \gt \beta _c$
it is ordered: disordered configurations resemble the all-out configuration (in that all components are of size
![]() $O(\log n)$
) whereas ordered configurations resemble the all-in configuration (where there is a giant component with
$O(\log n)$
) whereas ordered configurations resemble the all-in configuration (where there is a giant component with
![]() $\Omega (n)$
vertices). The two types of configurations coexist at
$\Omega (n)$
vertices). The two types of configurations coexist at
![]() $\beta =\beta _c$
, that is, each appears with some probability bounded away from zero. The methods in [Reference Helmuth, Jenssen and Perkins21] are based on cluster expansion techniques which also yielded an efficient sampling algorithm at all temperatures
$\beta =\beta _c$
, that is, each appears with some probability bounded away from zero. The methods in [Reference Helmuth, Jenssen and Perkins21] are based on cluster expansion techniques which also yielded an efficient sampling algorithm at all temperatures
![]() $\beta \gt 0$
. This is a surprising algorithmic result given that the coexistence causes multimodality in
$\beta \gt 0$
. This is a surprising algorithmic result given that the coexistence causes multimodality in
![]() $\pi _G$
and severe bottleneck phenomena for Markov chains in a window around
$\pi _G$
and severe bottleneck phenomena for Markov chains in a window around
![]() $\beta _c$
; it was shown for instance in [Reference Helmuth, Jenssen and Perkins21] that the RC dynamics (and the related non-local Swendsen–Wang dynamics) have exponential mixing time, essentially because of the number of steps needed for the chain to move from ordered to disordered (and vice versa).
$\beta _c$
; it was shown for instance in [Reference Helmuth, Jenssen and Perkins21] that the RC dynamics (and the related non-local Swendsen–Wang dynamics) have exponential mixing time, essentially because of the number of steps needed for the chain to move from ordered to disordered (and vice versa).
These results pose a rather bleak landscape for the RC dynamics; yet, on random regular graphs it is widely conjectured that the multimodality and the associated bottlenecks can be circumvented by initialising the chain more judiciously, in particular at either the all-out or the all-in configurations (depending on whether
![]() $\beta \leq \beta _c$
). However the tools available for analysing Markov chains are typically insensitive to the initial configuration, and even more so when working at a critical range of the parameters.
$\beta \leq \beta _c$
). However the tools available for analysing Markov chains are typically insensitive to the initial configuration, and even more so when working at a critical range of the parameters.
Our main result establishes this conjecture for all
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $q$
sufficiently large (conditions which we inherit from [Reference Helmuth, Jenssen and Perkins21]). For an integer
$q$
sufficiently large (conditions which we inherit from [Reference Helmuth, Jenssen and Perkins21]). For an integer
![]() $n$
such that
$n$
such that
![]() $\Delta n$
is even, let
$\Delta n$
is even, let
![]() ${\mathcal{G}}_{n,\Delta }$
denote the set of all
${\mathcal{G}}_{n,\Delta }$
denote the set of all
![]() $\Delta$
-regular graphs with
$\Delta$
-regular graphs with
![]() $n$
vertices.Footnote
2
Throughout, we use
$n$
vertices.Footnote
2
Throughout, we use
![]() $O(1)$
to denote a constant depending on
$O(1)$
to denote a constant depending on
![]() $q,\beta, \Delta$
but independent of
$q,\beta, \Delta$
but independent of
![]() $n$
.
$n$
.
Theorem 1.
Let
![]() $\Delta \geq 5$
be an integer. There exists
$\Delta \geq 5$
be an integer. There exists
![]() $C=C(\Delta )\gt 0$
such that, for all sufficiently large
$C=C(\Delta )\gt 0$
such that, for all sufficiently large
![]() $q$
, the following holds for any
$q$
, the following holds for any
![]() $\beta \gt 0$
, w.h.p. over
$\beta \gt 0$
, w.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
.
$G\sim{\mathcal{G}}_{n,\Delta }$
.
-
1. For
 $\beta \lt \beta _c$
, the mixing time of the RC dynamics starting from all-out is
$\beta \lt \beta _c$
, the mixing time of the RC dynamics starting from all-out is
 $O(n\log n).$
$O(n\log n).$
-
2. For
 $\beta \gt \beta _c$
, the mixing time of the RC dynamics starting from all-in is
$\beta \gt \beta _c$
, the mixing time of the RC dynamics starting from all-in is
 $O(n^{C})$
. For integer
$O(n^{C})$
. For integer
 $q$
, the mixing time is in fact
$q$
, the mixing time is in fact
 $O(n\log n)$
.
$O(n\log n)$
.
Note that Theorem1 implies a polynomial-time sampling algorithm from the Potts model for all
![]() $\beta \neq \beta _c$
(and all sufficiently large
$\beta \neq \beta _c$
(and all sufficiently large
![]() $q$
). Intuitively, and as we will see later in more detail, Theorem1 asserts that the RC dynamics starting from all-in mixes quickly within the set of ordered configurations for
$q$
). Intuitively, and as we will see later in more detail, Theorem1 asserts that the RC dynamics starting from all-in mixes quickly within the set of ordered configurations for
![]() $\beta \gt \beta _c$
, and similarly it mixes well within the disordered set of configurations starting from all out when
$\beta \gt \beta _c$
, and similarly it mixes well within the disordered set of configurations starting from all out when
![]() $\beta \lt \beta _c$
. In fact, we show that both of these remain true even for
$\beta \lt \beta _c$
. In fact, we show that both of these remain true even for
![]() $\beta =\beta _c$
and hence the RC dynamics can be used to sample even at criticality, starting from an appropriate mixture of the all-in and the all-out configurations. See Section 2 (and Section 2.4 in particular) for the exact statements.
$\beta =\beta _c$
and hence the RC dynamics can be used to sample even at criticality, starting from an appropriate mixture of the all-in and the all-out configurations. See Section 2 (and Section 2.4 in particular) for the exact statements.
Finally, note that the RC dynamics can be used analogously to Theorem1 to produce a sample within total variation distance
![]() $\varepsilon$
of
$\varepsilon$
of
![]() $\pi _G$
for any
$\pi _G$
for any
![]() $\varepsilon \geq \mathrm{e}^{-\Theta (n)}$
, by running it for a number of steps which is
$\varepsilon \geq \mathrm{e}^{-\Theta (n)}$
, by running it for a number of steps which is
![]() $\log (1/\varepsilon )$
times the corresponding mixing time bound.Footnote
3
The lower bound on the error comes from the total variation distance between
$\log (1/\varepsilon )$
times the corresponding mixing time bound.Footnote
3
The lower bound on the error comes from the total variation distance between
![]() $\pi _G$
and the conditional ‘ordered’ and ‘disordered’ configurations, see Lemma3.
$\pi _G$
and the conditional ‘ordered’ and ‘disordered’ configurations, see Lemma3.
1.1 Further related work
Our approach to proving Theorem1 is inspired from a recent paper by Gheissari and Sinclair [Reference Gheissari and Sinclair15] who established similar flavoured results for the Ising model (
![]() $q=2$
) on the random regular graph for large
$q=2$
) on the random regular graph for large
![]() $\beta$
. To obtain our results for all
$\beta$
. To obtain our results for all
![]() $\beta$
, we adapt suitably their notion of ‘spatial mixing within the phase’, see Section 2.2 for details.
$\beta$
, we adapt suitably their notion of ‘spatial mixing within the phase’, see Section 2.2 for details.
Among the results in [Reference Gheissari and Sinclair15], it was established that Glauber dynamics on the random regular graph, initialised appropriately, mixes in
![]() $O(n \log n)$
time when
$O(n \log n)$
time when
![]() $\beta$
is sufficiently large.Footnote
4
More recently, Gheissari and Sinclair [Reference Gheissari and Sinclair16] obtained mixing-time bounds for the RC dynamics on the lattice
$\beta$
is sufficiently large.Footnote
4
More recently, Gheissari and Sinclair [Reference Gheissari and Sinclair16] obtained mixing-time bounds for the RC dynamics on the lattice
![]() $\mathbb{Z}^d$
under appropriate boundary conditions. They also analyse the mixing time starting from a mixture of the all-in/all-out initialisation. Note that the phase transition on grid lattices is qualitatively different than that of the random regular graph; there, instead of a window/interval of temperatures, the three points
$\mathbb{Z}^d$
under appropriate boundary conditions. They also analyse the mixing time starting from a mixture of the all-in/all-out initialisation. Note that the phase transition on grid lattices is qualitatively different than that of the random regular graph; there, instead of a window/interval of temperatures, the three points
![]() $\beta _u,\beta _u^*$
and
$\beta _u,\beta _u^*$
and
![]() $\beta _c$
all coincide into a single phase transition point. See also [Reference Borgs, Chayes, Helmuth, Perkins and Tetali6,Reference Helmuth, Perkins and Regts22] for related algorithmic results on
$\beta _c$
all coincide into a single phase transition point. See also [Reference Borgs, Chayes, Helmuth, Perkins and Tetali6,Reference Helmuth, Perkins and Regts22] for related algorithmic results on
![]() $\mathbb{Z}^d$
using cluster expansion methods.
$\mathbb{Z}^d$
using cluster expansion methods.
For the random regular graph, Blanca and Gheissari [Reference Blanca and Gheissari4] showed for all integer
![]() $\Delta \geq 3$
and real
$\Delta \geq 3$
and real
![]() $q\geq 1$
that the mixing time is
$q\geq 1$
that the mixing time is
![]() $O(n\log n)$
provided that
$O(n\log n)$
provided that
![]() $\beta \lt \beta _u(q,\Delta )$
where
$\beta \lt \beta _u(q,\Delta )$
where
![]() $\beta _u$
is the uniqueness threshold on the tree. A sampling algorithm (not based on MCMC) for
$\beta _u$
is the uniqueness threshold on the tree. A sampling algorithm (not based on MCMC) for
![]() $\beta \lt \beta _c(q,\Delta )$
and
$\beta \lt \beta _c(q,\Delta )$
and
![]() $q,\Delta \geq 3$
was designed by Efthymiou [Reference Efthymiou12] (see also [Reference Blanca, Galanis, Goldberg, Štefankovič, Vigoda and Yang3]), albeit achieving weaker approximation guarantees. Coja-Oghlan, Galanis, Goldberg, Raveloman, Štefankovič, and Vigoda [Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Štefankovič and Vigoda10] showed that, for all integer
$q,\Delta \geq 3$
was designed by Efthymiou [Reference Efthymiou12] (see also [Reference Blanca, Galanis, Goldberg, Štefankovič, Vigoda and Yang3]), albeit achieving weaker approximation guarantees. Coja-Oghlan, Galanis, Goldberg, Raveloman, Štefankovič, and Vigoda [Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Štefankovič and Vigoda10] showed that, for all integer
![]() $q,\Delta \geq 3$
and
$q,\Delta \geq 3$
and
![]() $\beta \in (\beta _u,\beta _u')$
the mixing time is
$\beta \in (\beta _u,\beta _u')$
the mixing time is
![]() $\mathrm{e}^{\Omega (n)}$
where
$\mathrm{e}^{\Omega (n)}$
where
![]() $\beta _u'=\log (1+\tfrac{q}{\Delta -2})\gt \beta _u$
is (conjectured to be) another uniqueness threshold on the tree (see [Reference Häggström20,Reference Jonasson24]). More generally, for integer
$\beta _u'=\log (1+\tfrac{q}{\Delta -2})\gt \beta _u$
is (conjectured to be) another uniqueness threshold on the tree (see [Reference Häggström20,Reference Jonasson24]). More generally, for integer
![]() $q\geq 3$
, the hardness results/techniques of [Reference Galanis, Štefankovic, Vigoda and Yang14,Reference Goldberg and Jerrum17] yield that for any
$q\geq 3$
, the hardness results/techniques of [Reference Galanis, Štefankovic, Vigoda and Yang14,Reference Goldberg and Jerrum17] yield that for any
![]() $\beta \gt \beta _c$
, there are graphs
$\beta \gt \beta _c$
, there are graphs
![]() $G$
where the mixing time of the RC dynamics is
$G$
where the mixing time of the RC dynamics is
![]() $\exp (n^{\Omega (1)})$
and the problem of appoximately sampling on graphs of max-degree
$\exp (n^{\Omega (1)})$
and the problem of appoximately sampling on graphs of max-degree
![]() $\Delta$
becomes #BIS-hard; on the other hand, for
$\Delta$
becomes #BIS-hard; on the other hand, for
![]() $\beta \leq (1-o_{q,\Delta }(1))\beta _c$
it has been shown in [Reference Carlson, Davies, Fraiman, Kolla, Potukuchi and Yap7,Reference Coulson, Davies, Kolla, Patel and Regts11] that the cluster expansion technique of [Reference Helmuth, Jenssen and Perkins21] yields a sampling algorithm on any max-degree
$\beta \leq (1-o_{q,\Delta }(1))\beta _c$
it has been shown in [Reference Carlson, Davies, Fraiman, Kolla, Potukuchi and Yap7,Reference Coulson, Davies, Kolla, Patel and Regts11] that the cluster expansion technique of [Reference Helmuth, Jenssen and Perkins21] yields a sampling algorithm on any max-degree
![]() $\Delta$
graph.
$\Delta$
graph.
As a final note, another model of interest where analogous mixing results for Glauber dynamics (initialised appropriately) should be obtainable is for sampling independent sets on random bipartite regular graphs. However, in contrast to the RC/Potts models, the phase transition there is analogous to that of the Ising model, and hence, establishing the relevant spatial mixing properties close to the criticality threshold is likely to require different techniques, see, for example, [Reference Chen, Galanis, Štefankovič and Vigoda9] for more discussion.
In the next section, we outline the proof of Theorem1, explaining the main ingredients and showing how to combine them in order to conclude the proof. The rest of the paper is about establishing the main ingredients, see also Section 2.5 for a more detailed overview of the later parts.
1.2 Independent results of Blanca and gheissari
In an independent and simultaneous work, Blanca and Gheissari [Reference Blanca and Gheissari5] obtain related (but incomparable) results. For
![]() $\Delta \geq 3, q\geq 1$
and arbitrarily small
$\Delta \geq 3, q\geq 1$
and arbitrarily small
![]() $\tau \gt 0$
, they show for sufficiently large
$\tau \gt 0$
, they show for sufficiently large
![]() $\beta$
a mixing time bound of
$\beta$
a mixing time bound of
![]() $O(n^{1+\tau })$
for the RC dynamics on the random regular graph starting from an arbitrary configuration (and obtain an analogous result for the grid and the Swendsen–Wang dynamics). Our result instead applies to all
$O(n^{1+\tau })$
for the RC dynamics on the random regular graph starting from an arbitrary configuration (and obtain an analogous result for the grid and the Swendsen–Wang dynamics). Our result instead applies to all
![]() $\beta$
for the random regular graph (even the critical window) by taking into consideration the initial configuration; the two papers have different approaches to obtain the main ingredients.
$\beta$
for the random regular graph (even the critical window) by taking into consideration the initial configuration; the two papers have different approaches to obtain the main ingredients.
2. Proof of Theorem1
We start with the formal description of the RC dynamics. Given a graph
![]() $G=(V,E)$
and an initial configuration
$G=(V,E)$
and an initial configuration
![]() $X_0:E\rightarrow \{0,1\}$
, the RC dynamics on
$X_0:E\rightarrow \{0,1\}$
, the RC dynamics on
![]() $G$
is a Markov chain
$G$
is a Markov chain
![]() $(X_t)_{t\geq 0}$
on the set of configurations
$(X_t)_{t\geq 0}$
on the set of configurations
![]() $\Omega _G$
. Let
$\Omega _G$
. Let
![]() $p\;:\!=\;1-\mathrm{e}^{-\beta }$
and
$p\;:\!=\;1-\mathrm{e}^{-\beta }$
and
![]() $\hat{p}\;:\!=\;\tfrac{p}{(1-p)q+p}$
(note that for
$\hat{p}\;:\!=\;\tfrac{p}{(1-p)q+p}$
(note that for
![]() $q\gt 1$
it holds that
$q\gt 1$
it holds that
![]() $\hat{p}\in (p/q,p)$
). For
$\hat{p}\in (p/q,p)$
). For
![]() $t\geq 0$
, to obtain
$t\geq 0$
, to obtain
![]() $X_{t+1}$
from
$X_{t+1}$
from
![]() $X_t$
:
$X_t$
:
-
1. Choose u.a.r. an edge
 $e\in E$
. If
$e\in E$
. If
 $e$
is a cut-edge in the graph
$e$
is a cut-edge in the graph
 $(V,{\mathrm{In}}(X_t)\cup \{e\})$
, set
$(V,{\mathrm{In}}(X_t)\cup \{e\})$
, set
 $X_{t+1}(e)=1$
with probability
$X_{t+1}(e)=1$
with probability
 $\hat{p}$
(and
$\hat{p}$
(and
 $X_{t+1}(e)=0$
otherwise). Else, set
$X_{t+1}(e)=0$
otherwise). Else, set
 $X_{t+1}(e)=1$
with probability
$X_{t+1}(e)=1$
with probability
 $p$
, and
$p$
, and
 $X_{t+1}(e)=0$
otherwise.
$X_{t+1}(e)=0$
otherwise. -
2. Set
 $X_{t+1}(f)=X_t(f)$
for all
$X_{t+1}(f)=X_t(f)$
for all
 $f\in E\backslash \{e\}$
.
$f\in E\backslash \{e\}$
.
It is a standard fact that the distribution of
![]() $X_t$
converges to the RC distribution
$X_t$
converges to the RC distribution
![]() $\pi _G$
. Let
$\pi _G$
. Let
![]() $T_{\mathrm{mix}}(G;\;X_0)=\min _{t\geq 0} \{t\mid \mathrm{dist}_{\mathrm{TV}}(X_t,\pi _G)\leq 1/4\}$
be the number of steps needed to get within total variation distance
$T_{\mathrm{mix}}(G;\;X_0)=\min _{t\geq 0} \{t\mid \mathrm{dist}_{\mathrm{TV}}(X_t,\pi _G)\leq 1/4\}$
be the number of steps needed to get within total variation distance
![]() $\leq 1/4$
from
$\leq 1/4$
from
![]() $\pi _G$
starting from
$\pi _G$
starting from
![]() $X_0$
, and
$X_0$
, and
![]() $T_{\mathrm{mix}}(G)=\max _{X_0}T_{\mathrm{mix}}(G;X_0)$
be the mixing time from the worst starting state.
$T_{\mathrm{mix}}(G)=\max _{X_0}T_{\mathrm{mix}}(G;X_0)$
be the mixing time from the worst starting state.
2.1 The ordered and disordered phases on random regular graphs
We review in more detail the ordered/disordered transition, following [Reference Helmuth, Jenssen and Perkins21].
Definition 2.
For
![]() $\Delta \geq 3$
, let
$\Delta \geq 3$
, let
![]() $\eta =\eta (\Delta )\in (0,1/2)$
be a small constant (see Definition
19
). For
$\eta =\eta (\Delta )\in (0,1/2)$
be a small constant (see Definition
19
). For
![]() $G\in{\mathcal{G}}_{n,\Delta }$
, the ordered phase is the set of configurations
$G\in{\mathcal{G}}_{n,\Delta }$
, the ordered phase is the set of configurations
![]() $ \Omega ^{\mathrm{ord}}\;:\!=\; \{{\mathcal{F}}\in \Omega : |{\mathrm{In}}({\mathcal{F}})|\geq (1-\eta )|{E}|\}$
, whereas the disordered phase is the set
$ \Omega ^{\mathrm{ord}}\;:\!=\; \{{\mathcal{F}}\in \Omega : |{\mathrm{In}}({\mathcal{F}})|\geq (1-\eta )|{E}|\}$
, whereas the disordered phase is the set
![]() $ \Omega ^{\mathrm{dis}}\;:\!=\; \{{\mathcal{F}}\in \Omega : |{\mathrm{In}}({\mathcal{F}})|\leq \eta |{E}| \}$
. For
$ \Omega ^{\mathrm{dis}}\;:\!=\; \{{\mathcal{F}}\in \Omega : |{\mathrm{In}}({\mathcal{F}})|\leq \eta |{E}| \}$
. For
![]() $q,\beta \gt 0$
, let
$q,\beta \gt 0$
, let
![]() $\pi ^{\mathrm{ord}}_G,\pi ^{\mathrm{dis}}_G$
be the conditional distributions of
$\pi ^{\mathrm{ord}}_G,\pi ^{\mathrm{dis}}_G$
be the conditional distributions of
![]() $\pi _G$
on
$\pi _G$
on
![]() $\Omega ^{\mathrm{ord}},\Omega ^{\mathrm{dis}}$
, respectively.
$\Omega ^{\mathrm{ord}},\Omega ^{\mathrm{dis}}$
, respectively.
We will use the following result of Helmuth, Jenssen and Perkins [Reference Helmuth, Jenssen and Perkins21, Lemma9].
Lemma 3 ([Reference Helmuth, Jenssen and Perkins21, Theorem 1]). Let
![]() $\Delta \geq 5$
be an integer. Then, for all sufficiently large
$\Delta \geq 5$
be an integer. Then, for all sufficiently large
![]() $q$
, there exists
$q$
, there exists
![]() $\beta _c\gt 0$
satisfying
$\beta _c\gt 0$
satisfying
![]() $\beta _c=(1+o_q(1))\tfrac{2\log q}{\Delta }$
such that the following holds for any
$\beta _c=(1+o_q(1))\tfrac{2\log q}{\Delta }$
such that the following holds for any
![]() $\beta \gt 0$
w.h.p. for
$\beta \gt 0$
w.h.p. for
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
.
$G\sim{\mathcal{G}}_{n,\Delta }$
.
Moreover, there exists
![]() $\zeta =\zeta (\Delta )\gt 0$
with
$\zeta =\zeta (\Delta )\gt 0$
with
![]() $\zeta \lt \eta$
such that
$\zeta \lt \eta$
such that
 \begin{equation} \begin{aligned} \mbox{for $\beta \leq \beta _c$}, &\quad \pi _G^{\mathrm{dis}}\Big (|{\mathrm{In}}({\mathcal{F}})|\geq \zeta |E|\Big )=\mathrm{e}^{-\Omega (n)}, \quad \mbox{ and }\\[5pt] \mbox{for $\beta \geq \beta _c$}, &\quad \pi _G^{\mathrm{ord}}\Big (|{\mathrm{In}}({\mathcal{F}})|\leq (1-\zeta )|E|\Big )=\mathrm{e}^{-\Omega (n)}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mbox{for $\beta \leq \beta _c$}, &\quad \pi _G^{\mathrm{dis}}\Big (|{\mathrm{In}}({\mathcal{F}})|\geq \zeta |E|\Big )=\mathrm{e}^{-\Omega (n)}, \quad \mbox{ and }\\[5pt] \mbox{for $\beta \geq \beta _c$}, &\quad \pi _G^{\mathrm{ord}}\Big (|{\mathrm{In}}({\mathcal{F}})|\leq (1-\zeta )|E|\Big )=\mathrm{e}^{-\Omega (n)}. \end{aligned} \end{equation}
Proof. The claims about the total variation distance are shown in [Reference Helmuth, Jenssen and Perkins21, Theorem1, Items (2), (3), (8)]. Equation (2) shows a bit of slack in the definitions of
![]() $\Omega ^{\mathrm{dis}}$
and
$\Omega ^{\mathrm{dis}}$
and
![]() $\Omega ^{{\mathrm{ord}}}$
that will be useful later; it follows essentially from the same theorem, we defer the details to Lemma24.
$\Omega ^{{\mathrm{ord}}}$
that will be useful later; it follows essentially from the same theorem, we defer the details to Lemma24.
2.2 Main ingredient: weak spatial mixing within a phase
Let
![]() $G=(V,E)$
be a graph. For
$G=(V,E)$
be a graph. For
![]() $v\in V$
and
$v\in V$
and
![]() $r\geq 0$
, let
$r\geq 0$
, let
![]() $B_r(v)$
denote the set of all vertices in
$B_r(v)$
denote the set of all vertices in
![]() $V$
whose distance from
$V$
whose distance from
![]() $v$
is at most
$v$
is at most
![]() $r$
. Let
$r$
. Let
![]() $\pi =\pi _G$
be the RC distribution on
$\pi =\pi _G$
be the RC distribution on
![]() $G$
and let
$G$
and let
![]() $\pi _{{\mathcal{B}}_r^+(v)}$
be the conditional distribution of
$\pi _{{\mathcal{B}}_r^+(v)}$
be the conditional distribution of
![]() $\pi$
where all edges in
$\pi$
where all edges in
![]() $E\backslash E(B_r(v))$
are ‘in’. We define analogously
$E\backslash E(B_r(v))$
are ‘in’. We define analogously
![]() $\pi _{{\mathcal{B}}_r^-(v)}$
by conditioning the edges in
$\pi _{{\mathcal{B}}_r^-(v)}$
by conditioning the edges in
![]() $E\backslash E(B_r(v))$
to be ‘out’.
$E\backslash E(B_r(v))$
to be ‘out’.
Definition 4.
Let
![]() $G$
be a graph with
$G$
be a graph with
![]() $m$
edges. Let
$m$
edges. Let
![]() $q,\beta \gt 0$
be reals and
$q,\beta \gt 0$
be reals and
![]() $r\geq 1$
be an integer. We say that the graph
$r\geq 1$
be an integer. We say that the graph
![]() $G$
has WSM within the ordered phase at radius
$G$
has WSM within the ordered phase at radius
![]() $r$
if for every
$r$
if for every
![]() $v\in V(G)$
and every edge
$v\in V(G)$
and every edge
![]() $e$
incident to
$e$
incident to
![]() $v$
,
$v$
,
![]() $\Vert{\pi _{{\mathcal{B}}_r^+(v)}(e \mapsto \cdot ) - \pi ^{{\mathrm{ord}}}_G(e\mapsto \cdot ) }\Vert _{\mathrm{TV}} \leq \frac{1}{100m}$
. Analogously, we say that
$\Vert{\pi _{{\mathcal{B}}_r^+(v)}(e \mapsto \cdot ) - \pi ^{{\mathrm{ord}}}_G(e\mapsto \cdot ) }\Vert _{\mathrm{TV}} \leq \frac{1}{100m}$
. Analogously, we say that
![]() $G$
has WSM within the disordered phase at radius
$G$
has WSM within the disordered phase at radius
![]() $r$
if for every
$r$
if for every
![]() $v\in V(G)$
and every edge
$v\in V(G)$
and every edge
![]() $e$
incident to
$e$
incident to
![]() $v$
,
$v$
,
![]() $\Vert{\pi _{{\mathcal{B}}_r^-(v)}(e \mapsto \cdot ) - \pi ^{\mathrm{dis}}_G(e\mapsto \cdot ) }\Vert _{\mathrm{TV}} \leq \frac{1}{100m}$
.
$\Vert{\pi _{{\mathcal{B}}_r^-(v)}(e \mapsto \cdot ) - \pi ^{\mathrm{dis}}_G(e\mapsto \cdot ) }\Vert _{\mathrm{TV}} \leq \frac{1}{100m}$
.
The bulk of our arguments consists of showing the following two theorems.
Theorem 5.
Let
![]() $\Delta \geq 5$
be an integer. There exists
$\Delta \geq 5$
be an integer. There exists
![]() $M=M(\Delta )\gt 0$
such that for all
$M=M(\Delta )\gt 0$
such that for all
![]() $q$
sufficiently large, the following holds for any
$q$
sufficiently large, the following holds for any
![]() $\beta \geq \beta _c$
. W.h.p. over
$\beta \geq \beta _c$
. W.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
,
$G\sim{\mathcal{G}}_{n,\Delta }$
,
![]() $G$
has WSM within the ordered phase at a radius
$G$
has WSM within the ordered phase at a radius
![]() $r$
which satisfies
$r$
which satisfies
![]() $r\leq \tfrac{M}{\beta }\log n$
.
$r\leq \tfrac{M}{\beta }\log n$
.
The upper bound on the radius
![]() $r$
in terms of
$r$
in terms of
![]() $1/\beta$
ensures that we can remove the dependence on
$1/\beta$
ensures that we can remove the dependence on
![]() $\beta$
of the mixing time in Theorem1 (caused by a loose bound on the mixing time on the tree, see Lemma9 below). For the disordered phase, we have
$\beta$
of the mixing time in Theorem1 (caused by a loose bound on the mixing time on the tree, see Lemma9 below). For the disordered phase, we have
Theorem 6.
For all integer
![]() $\Delta \geq 5$
, for all
$\Delta \geq 5$
, for all
![]() $q$
sufficiently large and any
$q$
sufficiently large and any
![]() $\beta \leq \beta _c$
, w.h.p. over
$\beta \leq \beta _c$
, w.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
,
$G\sim{\mathcal{G}}_{n,\Delta }$
,
![]() $G$
has WSM within the disordered phase at a radius
$G$
has WSM within the disordered phase at a radius
![]() $r$
which satisfies
$r$
which satisfies
![]() $r\leq \tfrac{1}{3}\log _{\Delta -1}\!n$
.
$r\leq \tfrac{1}{3}\log _{\Delta -1}\!n$
.
2.3 Second ingredient: local mixing on tree-like neighbourhoods
We first define a local version of RC dynamics where we perform only updates in a small ball around a vertex. Here, we need to consider the extreme boundary conditions that all vertices outside of the ball belong in distinct components (‘free boundary’) and where they belong to the same component (‘wired boundary’); we will refer to these two chains as the free and wired RC dynamics, respectively. For the random regular graph, these ‘local-mixing’ considerations are strongly connnected to the
![]() $\Delta$
-regular tree.
$\Delta$
-regular tree.
Formally, given a graph
![]() $G=(V,E)$
and a subset
$G=(V,E)$
and a subset
![]() $U\subseteq V$
, let
$U\subseteq V$
, let
![]() $G[U]$
be the induced subgraph of
$G[U]$
be the induced subgraph of
![]() $G$
on
$G$
on
![]() $U$
. The tree excess of a connected graph
$U$
. The tree excess of a connected graph
![]() $G$
is given by
$G$
is given by
![]() $|E|-|V|+1$
. For a vertex
$|E|-|V|+1$
. For a vertex
![]() $v$
in
$v$
in
![]() $G$
and integer
$G$
and integer
![]() $r\geq 0$
, let
$r\geq 0$
, let
![]() $B_r(v)$
denote the set of vertices at distance at most
$B_r(v)$
denote the set of vertices at distance at most
![]() $r$
from
$r$
from
![]() $v$
and
$v$
and
![]() $S_r(v)$
those at distance exactly
$S_r(v)$
those at distance exactly
![]() $r$
from
$r$
from
![]() $v$
. For
$v$
. For
![]() $K\gt 0$
, a max-degree
$K\gt 0$
, a max-degree
![]() $\Delta$
graph
$\Delta$
graph
![]() $G$
is locally
$G$
is locally
![]() $K$
-treelike if for every
$K$
-treelike if for every
![]() $v\in V$
and
$v\in V$
and
![]() $r\leq \frac{1}{3}\log _{\Delta -1}|V|$
, the graph
$r\leq \frac{1}{3}\log _{\Delta -1}|V|$
, the graph
![]() $G[B_r(v)]$
has tree excess
$G[B_r(v)]$
has tree excess
![]() $\leq K$
.
$\leq K$
.
Lemma 7 (see, e.g., [Reference Gheissari and Sinclair15, Lemma 5.8], [Reference Blanca and Gheissari4, Fact 2.3]). For any integer
![]() $\Delta \geq 3$
, there is
$\Delta \geq 3$
, there is
![]() $K\gt 0$
such that w.h.p.
$K\gt 0$
such that w.h.p.
![]() $G\sim G_{n,\Delta }$
is locally
$G\sim G_{n,\Delta }$
is locally
![]() $K$
-treelike.
$K$
-treelike.
For a graph
![]() $G$
, a vertex
$G$
, a vertex
![]() $\rho$
in
$\rho$
in
![]() $G$
and an integer
$G$
and an integer
![]() $r\geq 1$
, the free RC dynamics on
$r\geq 1$
, the free RC dynamics on
![]() $B_r(\rho )$
is the RC dynamics where all edges outside of
$B_r(\rho )$
is the RC dynamics where all edges outside of
![]() $B_r(\rho )$
are conditioned to be out and only edges of
$B_r(\rho )$
are conditioned to be out and only edges of
![]() $G$
with both endpoints in
$G$
with both endpoints in
![]() $B_r(\rho )$
are updated.
$B_r(\rho )$
are updated.
Lemma 8 ([Reference Blanca and Gheissari4, Lemma 6.5]). Let
![]() $\Delta \geq 3$
be an integer, and
$\Delta \geq 3$
be an integer, and
![]() $q,K\gt 1$
,
$q,K\gt 1$
,
![]() $\beta \gt 0$
be reals. There exists
$\beta \gt 0$
be reals. There exists
![]() $C\gt 0$
such that the following holds for any
$C\gt 0$
such that the following holds for any
![]() $\Delta$
-regular graph
$\Delta$
-regular graph
![]() $G$
and integer
$G$
and integer
![]() $r\geq 1$
.
$r\geq 1$
.
Suppose that
![]() $\rho \in V$
is such that
$\rho \in V$
is such that
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. Then, with
$K$
-treelike. Then, with
![]() $n=|B_r(\rho )|$
, the mixing time of the free RC dynamics on
$n=|B_r(\rho )|$
, the mixing time of the free RC dynamics on
![]() $B_r(\rho )$
is
$B_r(\rho )$
is
![]() $\leq Cn\log n$
.
$\leq Cn\log n$
.
To define the wired RC dynamics, for a graph
![]() $G$
, a vertex
$G$
, a vertex
![]() $\rho$
in
$\rho$
in
![]() $G$
and an integer
$G$
and an integer
![]() $r\geq 1$
, let
$r\geq 1$
, let
![]() $H$
be the graph obtained by removing all vertices and edges outside of
$H$
be the graph obtained by removing all vertices and edges outside of
![]() $B_r(\rho )$
, and adding a new vertex
$B_r(\rho )$
, and adding a new vertex
![]() $v_{\infty }$
connected to all vertices in
$v_{\infty }$
connected to all vertices in
![]() $S_r(\rho )$
. The wired RC dynamics on
$S_r(\rho )$
. The wired RC dynamics on
![]() $B_r(\rho )$
is the RC dynamics on
$B_r(\rho )$
is the RC dynamics on
![]() $H$
where the edges adjacent to
$H$
where the edges adjacent to
![]() $v_\infty$
are conditioned to be in and only edges of
$v_\infty$
are conditioned to be in and only edges of
![]() $G$
with both endpoints in
$G$
with both endpoints in
![]() $B_r(\rho )$
are updated. Denote by
$B_r(\rho )$
are updated. Denote by
![]() $\hat{\pi }_{B_r(\rho )}$
the stationary distribution of the wired RC dynamics. Note that when the graph outside of
$\hat{\pi }_{B_r(\rho )}$
the stationary distribution of the wired RC dynamics. Note that when the graph outside of
![]() $B_r(\rho )$
is connected,
$B_r(\rho )$
is connected,
![]() $\hat{\pi }_{B_r(\rho )}$
induces the same distribution as
$\hat{\pi }_{B_r(\rho )}$
induces the same distribution as
![]() $\pi _{{\mathcal{B}}^+_r(\rho )}$
.Footnote
5
$\pi _{{\mathcal{B}}^+_r(\rho )}$
.Footnote
5
Lemma 9.
Let
![]() $\Delta \geq 3$
be an integer, and
$\Delta \geq 3$
be an integer, and
![]() $q,K\gt 1$
,
$q,K\gt 1$
,
![]() $\beta \gt 0$
be reals. There exists
$\beta \gt 0$
be reals. There exists
![]() $\hat{C}\gt 0$
such that the following holds for every
$\hat{C}\gt 0$
such that the following holds for every
![]() $\Delta$
-regular graph
$\Delta$
-regular graph
![]() $G=(V,E)$
and any integer
$G=(V,E)$
and any integer
![]() $r\geq 1$
.
$r\geq 1$
.
Suppose that
![]() $\rho \in V$
is such that
$\rho \in V$
is such that
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. Then, with
$K$
-treelike. Then, with
![]() $n=|B_r(\rho )|$
, the mixing time of the wired RC dynamics on
$n=|B_r(\rho )|$
, the mixing time of the wired RC dynamics on
![]() $B_r(\rho )$
is
$B_r(\rho )$
is
![]() $\leq \hat{C}n^3(q^{4}\mathrm{e}^{\beta })^{\Delta r}$
.
$\leq \hat{C}n^3(q^{4}\mathrm{e}^{\beta })^{\Delta r}$
.
Lemma9 is proved in Appendix A.
2.4 Proof of Theorem 1
Assuming for now the above ingredients, we will conclude the proof of Theorem1. For clarity, we break up the latter into the following pieces.
Theorem 11 (Convergence to ordered for real
![]() $q$
). Let
$q$
). Let
![]() $\Delta \geq 5$
be an integer. Then, for all sufficiently large
$\Delta \geq 5$
be an integer. Then, for all sufficiently large
![]() $q$
, there exists
$q$
, there exists
![]() $C=C(\Delta )$
such that the following holds for
$C=C(\Delta )$
such that the following holds for
![]() $\beta \geq \beta _c$
, w.h.p. over
$\beta \geq \beta _c$
, w.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
. The RC dynamics
$G\sim{\mathcal{G}}_{n,\Delta }$
. The RC dynamics
![]() $(X_t)_{t\geq 0}$
on
$(X_t)_{t\geq 0}$
on
![]() $G$
starting from all-in satisfies
$G$
starting from all-in satisfies
![]() $\mathrm{dist}_{\mathrm{TV}}(X_T,\pi _G^{\mathrm{ord}})\leq 1/5$
for
$\mathrm{dist}_{\mathrm{TV}}(X_T,\pi _G^{\mathrm{ord}})\leq 1/5$
for
![]() $T=O(n^{C})$
.
$T=O(n^{C})$
.
Theorem 12 (Convergence to disordered for real
![]() $q$
). Let
$q$
). Let
![]() $\Delta \geq 5$
be an integer. Then, for all sufficiently large
$\Delta \geq 5$
be an integer. Then, for all sufficiently large
![]() $q$
and
$q$
and
![]() $\beta \leq \beta _c$
, w.h.p. over
$\beta \leq \beta _c$
, w.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
, the RC dynamics
$G\sim{\mathcal{G}}_{n,\Delta }$
, the RC dynamics
![]() $(X_t)_{t\geq 0}$
on
$(X_t)_{t\geq 0}$
on
![]() $G$
starting from all-in satisfies
$G$
starting from all-in satisfies
![]() $\mathrm{dist}_{\mathrm{TV}}(X_T,\pi ^{\mathrm{dis}}_G)\leq 1/5$
for
$\mathrm{dist}_{\mathrm{TV}}(X_T,\pi ^{\mathrm{dis}}_G)\leq 1/5$
for
![]() $T=O(n\log n)$
.
$T=O(n\log n)$
.
Theorem 13 (Faster convergence to ordered for integer
![]() $q$
). Let
$q$
). Let
![]() $\Delta \geq 5$
be an integer. Then, for all sufficiently large integer
$\Delta \geq 5$
be an integer. Then, for all sufficiently large integer
![]() $q$
and
$q$
and
![]() $\beta \geq \beta _c$
, w.h.p. over
$\beta \geq \beta _c$
, w.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
, the RC dynamics
$G\sim{\mathcal{G}}_{n,\Delta }$
, the RC dynamics
![]() $(X_t)_{t\geq 0}$
on
$(X_t)_{t\geq 0}$
on
![]() $G$
starting from all-in satisfies
$G$
starting from all-in satisfies
![]() $\mathrm{dist}_{\mathrm{TV}}(X_T,\pi ^{\mathrm{dis}}_G)\leq 1/5$
for
$\mathrm{dist}_{\mathrm{TV}}(X_T,\pi ^{\mathrm{dis}}_G)\leq 1/5$
for
![]() $T=O(n\log n)$
.
$T=O(n\log n)$
.
Using these, the proof of Theorem1 can be concluded easily.
Proof of Theorem
1. Follows immediately by Theorems11-13, since by Lemma3 we have that
![]() $\left \| \pi _G-\pi _G^{\mathrm{ord}}\right \|_{\mathrm{TV}}=\mathrm{e}^{-\Omega (n)}$
when
$\left \| \pi _G-\pi _G^{\mathrm{ord}}\right \|_{\mathrm{TV}}=\mathrm{e}^{-\Omega (n)}$
when
![]() $\beta \gt \beta _c$
and
$\beta \gt \beta _c$
and
![]() $\left \| \pi _G-\pi _G^{\mathrm{dis}}\right \|_{\mathrm{TV}}=\mathrm{e}^{-\Omega (n)}$
.
$\left \| \pi _G-\pi _G^{\mathrm{dis}}\right \|_{\mathrm{TV}}=\mathrm{e}^{-\Omega (n)}$
.
We next show how to combine the ingredients of Sections 2.1-2.3 in order to conclude Theorem11. The proofs of Theorems12 and 13 are very similar, but involve one more technical tool in order to conclude the
![]() $O(n\log n)$
bounds. We defer their proof to Section 7.
$O(n\log n)$
bounds. We defer their proof to Section 7.
Proof of Theorem
11. The argument resembles that of [Reference Gheissari and Sinclair15], a bit of care is required to combine the pieces. Consider
![]() $G=(V,E)\sim{\mathcal{G}}_{n,\Delta }$
with
$G=(V,E)\sim{\mathcal{G}}_{n,\Delta }$
with
![]() $n=|V|$
and
$n=|V|$
and
![]() $m=|E|$
. Let
$m=|E|$
. Let
![]() $q$
be sufficiently large so that both Lemma3 and Theorem5 apply; assume also that Lemma7 applies so that
$q$
be sufficiently large so that both Lemma3 and Theorem5 apply; assume also that Lemma7 applies so that
![]() $G$
is locally
$G$
is locally
![]() $K$
-treelike. By Lemma3, for every
$K$
-treelike. By Lemma3, for every
![]() $\beta \geq \beta _c$
,
$\beta \geq \beta _c$
,
![]() $\pi _G^{\mathrm{ord}}\big (|{\mathrm{In}}({\mathcal{F}})|\leq (1-\zeta )|E|\big )=\mathrm{e}^{-\Omega (n)}$
.
$\pi _G^{\mathrm{ord}}\big (|{\mathrm{In}}({\mathcal{F}})|\leq (1-\zeta )|E|\big )=\mathrm{e}^{-\Omega (n)}$
.
From now on consider arbitrary
![]() $\beta \geq \beta _c$
and set
$\beta \geq \beta _c$
and set
![]() $\beta _0\;:\!=\;\log (q^{1.9/\Delta }+1)$
. Since
$\beta _0\;:\!=\;\log (q^{1.9/\Delta }+1)$
. Since
![]() $\beta _c=(1+o_q(1))\tfrac{2\log q}{\Delta }$
, we have that
$\beta _c=(1+o_q(1))\tfrac{2\log q}{\Delta }$
, we have that
![]() $\beta \geq \beta _0$
for all sufficiently large
$\beta \geq \beta _0$
for all sufficiently large
![]() $q$
. Moreover, by Theorem5,
$q$
. Moreover, by Theorem5,
![]() $G$
has WSM within the ordered phase at radius
$G$
has WSM within the ordered phase at radius
![]() $r$
for some
$r$
for some
![]() $r\leq \tfrac{M}{\beta }\log n$
, where
$r\leq \tfrac{M}{\beta }\log n$
, where
![]() $M=M(\Delta )\gt 0$
is a constant independent of
$M=M(\Delta )\gt 0$
is a constant independent of
![]() $\beta$
. Note that by taking
$\beta$
. Note that by taking
![]() $q$
large, we can ensure that
$q$
large, we can ensure that
![]() $\beta _0$
and hence
$\beta _0$
and hence
![]() $\beta$
are at least
$\beta$
are at least
![]() $3M\log (\Delta -1)$
so that
$3M\log (\Delta -1)$
so that
![]() $r\leq \tfrac{1}{3}\log _{\Delta -1}n$
(and hence the radius-
$r\leq \tfrac{1}{3}\log _{\Delta -1}n$
(and hence the radius-
![]() $r$
neighbourhood of an arbitrary vertex in
$r$
neighbourhood of an arbitrary vertex in
![]() $G$
is locally
$G$
is locally
![]() $K$
-treelike).
$K$
-treelike).
We will consider the RC dynamics
![]() $(X_t)_{t\geq 0}$
with
$(X_t)_{t\geq 0}$
with
![]() $X_0$
being the all-in configuration on the edges. We will also consider the ‘ordered’ RC dynamics
$X_0$
being the all-in configuration on the edges. We will also consider the ‘ordered’ RC dynamics
![]() $\hat{X}_t$
with
$\hat{X}_t$
with
![]() $\hat{X}_0\sim \pi ^{\mathrm{ord}}_G$
where we reject moves that lead to configurations outside of
$\hat{X}_0\sim \pi ^{\mathrm{ord}}_G$
where we reject moves that lead to configurations outside of
![]() $\Omega ^{{\mathrm{ord}}}$
; since
$\Omega ^{{\mathrm{ord}}}$
; since
![]() $\hat{X}_0$
is stationary note that
$\hat{X}_0$
is stationary note that
![]() $\hat{X}_t\sim \pi ^{\mathrm{ord}}_G$
for all
$\hat{X}_t\sim \pi ^{\mathrm{ord}}_G$
for all
![]() $t\geq 0$
. We will show how to couple these two dynamics in
$t\geq 0$
. We will show how to couple these two dynamics in
![]() $O(n^C)$
steps. The theorem will follow by showing that
$O(n^C)$
steps. The theorem will follow by showing that
![]() ${\mathrm{dist}}_{\mathrm{TV}}(X_T,\hat{X}_T)\leq 1/5$
, where
${\mathrm{dist}}_{\mathrm{TV}}(X_T,\hat{X}_T)\leq 1/5$
, where
![]() $T=O(n^{2+\log W})$
with
$T=O(n^{2+\log W})$
with
![]() $W=\Delta ^{2M/\beta _0} \mathrm{e}^{M \Delta (\Delta +1)}$
being independent of
$W=\Delta ^{2M/\beta _0} \mathrm{e}^{M \Delta (\Delta +1)}$
being independent of
![]() $\beta$
.
$\beta$
.
Consider the dynamics
![]() $(X_t)_{t\geq 0}$
and
$(X_t)_{t\geq 0}$
and
![]() $(\hat{X}_t)_{t\geq 0}$
. For
$(\hat{X}_t)_{t\geq 0}$
. For
![]() $t\geq 0$
, let
$t\geq 0$
, let
![]() $\mathcal{E}_t$
be the event that
$\mathcal{E}_t$
be the event that
![]() ${\mathrm{In}}(\hat{X}_t)\geq (1-\zeta )|E|$
and let
${\mathrm{In}}(\hat{X}_t)\geq (1-\zeta )|E|$
and let
![]() $\mathcal{E}_{\lt t}\;:\!=\;\bigcap _{t'=0,\ldots, t-1} \mathcal{E}_{t'}$
. From Lemma3 we have that
$\mathcal{E}_{\lt t}\;:\!=\;\bigcap _{t'=0,\ldots, t-1} \mathcal{E}_{t'}$
. From Lemma3 we have that
![]() $\pi ^{{\mathrm{ord}}}_G(\mathcal{E}_t)\geq 1-\mathrm{e}^{-\Omega (n)}$
and hence by a union bound
$\pi ^{{\mathrm{ord}}}_G(\mathcal{E}_t)\geq 1-\mathrm{e}^{-\Omega (n)}$
and hence by a union bound
![]() $\pi ^{{\mathrm{ord}}}_G(\mathcal{E}_{\lt t})\geq 1-t\mathrm{e}^{-\Omega (n)}$
as well.
$\pi ^{{\mathrm{ord}}}_G(\mathcal{E}_{\lt t})\geq 1-t\mathrm{e}^{-\Omega (n)}$
as well.
We couple the evolution of
![]() $X_t$
and
$X_t$
and
![]() $\hat{X}_t$
using the monotone coupling, that is, at every step of the two chains choose the same edge
$\hat{X}_t$
using the monotone coupling, that is, at every step of the two chains choose the same edge
![]() $e_t$
to update and use the same uniform number
$e_t$
to update and use the same uniform number
![]() $U_t\in [0,1]$
to decide whether to include
$U_t\in [0,1]$
to decide whether to include
![]() $e_t$
in each of
$e_t$
in each of
![]() $X_{t+1},\hat{X}_{t+1}$
. Using the monotonicity of the model for
$X_{t+1},\hat{X}_{t+1}$
. Using the monotonicity of the model for
![]() $q\geq 1$
(and in particular that
$q\geq 1$
(and in particular that
![]() $p\gt \hat{p}$
), under the monotone coupling, for all
$p\gt \hat{p}$
), under the monotone coupling, for all
![]() $t\geq 0$
such that
$t\geq 0$
such that
![]() $\mathcal{E}_{\lt t}$
holds (and hence no reject move has happened in
$\mathcal{E}_{\lt t}$
holds (and hence no reject move has happened in
![]() $\hat{X}_t$
so far), we have that
$\hat{X}_t$
so far), we have that
![]() $\hat{X}_t\leq X_t$
(i.e.,
$\hat{X}_t\leq X_t$
(i.e.,
![]() ${\mathrm{In}}(\hat{X}_t)\subseteq{\mathrm{In}}(X_t)$
). To complete the proof, it therefore suffices to show that
${\mathrm{In}}(\hat{X}_t)\subseteq{\mathrm{In}}(X_t)$
). To complete the proof, it therefore suffices to show that
Consider an arbitrary time
![]() $t\geq 0$
. By a union bound, we have that
$t\geq 0$
. By a union bound, we have that
Fix an arbitrary edge
![]() $e$
incident to some vertex
$e$
incident to some vertex
![]() $v$
, and let
$v$
, and let
![]() $(X^v_t)$
be the wired RC dynamics on
$(X^v_t)$
be the wired RC dynamics on
![]() $G[B_r(v)]$
. We couple the evolution of
$G[B_r(v)]$
. We couple the evolution of
![]() $(X_t^v)$
with that of
$(X_t^v)$
with that of
![]() $(X_t)$
and
$(X_t)$
and
![]() $(\hat{X}_t)$
using the monotone coupling analogously to above, where in
$(\hat{X}_t)$
using the monotone coupling analogously to above, where in
![]() $X_t^v$
we ignore updates of edges outside the ball
$X_t^v$
we ignore updates of edges outside the ball
![]() $G[B_r(v)]$
). We have
$G[B_r(v)]$
). We have
![]() $X_t^v\geq X_t$
for all
$X_t^v\geq X_t$
for all
![]() $t\geq 0$
, and hence, conditioned on
$t\geq 0$
, and hence, conditioned on
![]() $\mathcal{E}_{\lt t}$
, we have that
$\mathcal{E}_{\lt t}$
, we have that
![]() $X^v_t\geq X_t\geq \hat{X}_t$
. It follows that
$X^v_t\geq X_t\geq \hat{X}_t$
. It follows that
 \begin{align*}{\mathbb{P}}\big (X_t(e)\neq \hat{X}_t(e)\mid \mathcal{E}_{\lt t}\big )&={\mathbb{P}}(X_t(e)=1\mid \mathcal{E}_{\lt t})-{\mathbb{P}}(\hat{X}_t(e)=1\mid \mathcal{E}_{\lt t})\\[5pt] &\leq |{\mathbb{P}}(X^v_t(e)=1\mid \mathcal{E}_{\lt t})-{\mathbb{P}}(\hat{X}_t(e)=1\mid \mathcal{E}_{\lt t})|. \end{align*}
\begin{align*}{\mathbb{P}}\big (X_t(e)\neq \hat{X}_t(e)\mid \mathcal{E}_{\lt t}\big )&={\mathbb{P}}(X_t(e)=1\mid \mathcal{E}_{\lt t})-{\mathbb{P}}(\hat{X}_t(e)=1\mid \mathcal{E}_{\lt t})\\[5pt] &\leq |{\mathbb{P}}(X^v_t(e)=1\mid \mathcal{E}_{\lt t})-{\mathbb{P}}(\hat{X}_t(e)=1\mid \mathcal{E}_{\lt t})|. \end{align*}
For any two events
![]() $A,B$
, we have
$A,B$
, we have
![]() $|{\mathbb{P}}(A)-{\mathbb{P}}(A\mid B)|\leq 2{\mathbb{P}}(\overline{B})$
, so using this for
$|{\mathbb{P}}(A)-{\mathbb{P}}(A\mid B)|\leq 2{\mathbb{P}}(\overline{B})$
, so using this for
![]() $B=\mathcal{E}_{\lt t}$
and
$B=\mathcal{E}_{\lt t}$
and
![]() $A$
the events
$A$
the events
![]() $\{X^v_t(e)=1\},\{\hat{X}_t(e)=1\}$
, the triangle inequality gives
$\{X^v_t(e)=1\},\{\hat{X}_t(e)=1\}$
, the triangle inequality gives
Note that
![]() ${\mathbb{P}}(\hat{X}_t(e)=1)=\pi ^{{\mathrm{ord}}}_G(e\mapsto 1)$
, so another application of triangle inequality gives
${\mathbb{P}}(\hat{X}_t(e)=1)=\pi ^{{\mathrm{ord}}}_G(e\mapsto 1)$
, so another application of triangle inequality gives
 \begin{equation} \begin{aligned}{\mathbb{P}}\big (X_t(e)\neq \hat{X}_t(e)\mid \mathcal{E}_{\lt t}\big )\leq 4{\mathbb{P}}\big (\overline{ \mathcal{E}_{\lt t}}\big )+\big |{\mathbb{P}}(X^v_t(e)&=1)-\pi _{{\mathcal{B}}^+_r(v)}(e\mapsto 1)\big |\\[5pt] &+\big |\pi _{{\mathcal{B}}^+_r(v)}(e\mapsto 1)-\pi ^{{\mathrm{ord}}}_G(e\mapsto 1)\big |. \end{aligned} \end{equation}
\begin{equation} \begin{aligned}{\mathbb{P}}\big (X_t(e)\neq \hat{X}_t(e)\mid \mathcal{E}_{\lt t}\big )\leq 4{\mathbb{P}}\big (\overline{ \mathcal{E}_{\lt t}}\big )+\big |{\mathbb{P}}(X^v_t(e)&=1)-\pi _{{\mathcal{B}}^+_r(v)}(e\mapsto 1)\big |\\[5pt] &+\big |\pi _{{\mathcal{B}}^+_r(v)}(e\mapsto 1)-\pi ^{{\mathrm{ord}}}_G(e\mapsto 1)\big |. \end{aligned} \end{equation}
Since
![]() $G$
has WSM within the ordered phase at radius
$G$
has WSM within the ordered phase at radius
![]() $r$
, we have that
$r$
, we have that
Moreover, let
![]() $T_v$
be the mixing time of the wired RC dynamics on
$T_v$
be the mixing time of the wired RC dynamics on
![]() $G[B_r(v)]$
and let
$G[B_r(v)]$
and let
![]() $N_v=|E(B_r(v))|\leq \Delta ^{r+1}$
. Since
$N_v=|E(B_r(v))|\leq \Delta ^{r+1}$
. Since
![]() $r\leq \tfrac{1}{3}\log _{\Delta -1} n$
,
$r\leq \tfrac{1}{3}\log _{\Delta -1} n$
,
![]() $G[B_r(v)]$
is
$G[B_r(v)]$
is
![]() $K$
-treelike, so from Lemma9, with
$K$
-treelike, so from Lemma9, with
![]() $\hat{C}=O(1)$
denoting the constant there (and absorbing a couple of factors of
$\hat{C}=O(1)$
denoting the constant there (and absorbing a couple of factors of
![]() $\Delta$
into it),
$\Delta$
into it),
where in the last inequality we used that
![]() $\beta \gt \beta _0$
,
$\beta \gt \beta _0$
,
![]() $\beta _0\gt \tfrac{1}{\Delta }\log q$
and
$\beta _0\gt \tfrac{1}{\Delta }\log q$
and
![]() $W=\Delta ^{2M/\beta _0} \mathrm{e}^{M \Delta (\Delta +1)}$
. For
$W=\Delta ^{2M/\beta _0} \mathrm{e}^{M \Delta (\Delta +1)}$
. For
![]() $T=\Theta (n^{2+\log W})$
, we have
$T=\Theta (n^{2+\log W})$
, we have
![]() $T\geq 40T_v \tfrac{m}{N_v}\log m$
, so by Chernoff bounds, with probability
$T\geq 40T_v \tfrac{m}{N_v}\log m$
, so by Chernoff bounds, with probability
![]() $1-\exp (-n^{\Omega (1)})$
, we have at least
$1-\exp (-n^{\Omega (1)})$
, we have at least
![]() $10T_v \log m$
updates inside
$10T_v \log m$
updates inside
![]() $B_r(v)$
among
$B_r(v)$
among
![]() $t=1,\ldots, T$
. For integer
$t=1,\ldots, T$
. For integer
![]() $k\geq 1$
the distance from stationarity after
$k\geq 1$
the distance from stationarity after
![]() $kT_v$
steps is at most
$kT_v$
steps is at most
![]() $(1/4)^k$
, we obtain
$(1/4)^k$
, we obtain
Plugging (6) and (7) into (5) for
![]() $t=T$
, and then back into (4), we obtain using
$t=T$
, and then back into (4), we obtain using
![]() ${\mathbb{P}}(\overline{\mathcal{E}_{\lt T}})\leq T\mathrm{e}^{-\Omega (n)}$
that
${\mathbb{P}}(\overline{\mathcal{E}_{\lt T}})\leq T\mathrm{e}^{-\Omega (n)}$
that
![]() ${\mathbb{P}}(X_T\neq \hat{X}_T)\leq 5m T \mathrm{e}^{-\Omega (n)}+m/m^3+1/100\leq 1/5$
, as needed.
${\mathbb{P}}(X_T\neq \hat{X}_T)\leq 5m T \mathrm{e}^{-\Omega (n)}+m/m^3+1/100\leq 1/5$
, as needed.
Remark 14.
The value
![]() $T$
in the proof of Theorem
11
gives the running time
$T$
in the proof of Theorem
11
gives the running time
![]() $O(n^{C(\Delta )})$
in the statement. In particular,
$O(n^{C(\Delta )})$
in the statement. In particular,
![]() $T = \Theta (n^{2 + \log W})$
where
$T = \Theta (n^{2 + \log W})$
where
![]() $W=\Delta ^{2M/\beta _0} \mathrm{e}^{M \Delta (\Delta +1)}$
,
$W=\Delta ^{2M/\beta _0} \mathrm{e}^{M \Delta (\Delta +1)}$
,
![]() $\beta _0 \gt \log (q)/\Delta$
, and
$\beta _0 \gt \log (q)/\Delta$
, and
![]() $M = \Theta (\Delta \log \Delta )$
(see the start of Section
5
) so
$M = \Theta (\Delta \log \Delta )$
(see the start of Section
5
) so
![]() $C(\Delta ) = O(\Delta ^3 \log \Delta )$
.
$C(\Delta ) = O(\Delta ^3 \log \Delta )$
.
To get the improved mixing time bounds of
![]() $O(n\log n)$
in Theorems12 and 13 the reasoning is very similar. The main difference from the above proof is that for any vertex
$O(n\log n)$
in Theorems12 and 13 the reasoning is very similar. The main difference from the above proof is that for any vertex
![]() $v$
the mixing time
$v$
the mixing time
![]() $T_v$
is bounded by
$T_v$
is bounded by
![]() $T_v=O( N_v \log N_v)$
, and therefore the above argument yields a mixing time upper bound of
$T_v=O( N_v \log N_v)$
, and therefore the above argument yields a mixing time upper bound of
![]() $O(n(\log n)^2)$
so a bit more care is needed to remove the extra
$O(n(\log n)^2)$
so a bit more care is needed to remove the extra
![]() $\log n$
factor using a log-Sobolev inequality, the details can be found in Section 7.3.
$\log n$
factor using a log-Sobolev inequality, the details can be found in Section 7.3.
Finally, note that Theorems11, 12 and 13 all apply to the critical case
![]() $\beta =\beta _c$
as well. The only difference at criticality is that the two phases coexist [Reference Helmuth, Jenssen and Perkins21] (i.e., each appears with
$\beta =\beta _c$
as well. The only difference at criticality is that the two phases coexist [Reference Helmuth, Jenssen and Perkins21] (i.e., each appears with
![]() $\Omega (1)$
probability), so in order to obtain a sample from
$\Omega (1)$
probability), so in order to obtain a sample from
![]() $\pi _G$
, one should output a sample for
$\pi _G$
, one should output a sample for
![]() $\pi ^{{\mathrm{ord}}}_G$
with some probability
$\pi ^{{\mathrm{ord}}}_G$
with some probability
![]() $Q$
and otherwise a sample from
$Q$
and otherwise a sample from
![]() $\pi ^{\mathrm{dis}}_G$
. The value of
$\pi ^{\mathrm{dis}}_G$
. The value of
![]() $Q$
can be computed in time
$Q$
can be computed in time
![]() $\tilde{O}(n^2)$
by approximating the corresponding partition functions, by using, for example, the algorithms in [Reference Chen, Galanis, Goldberg, Perkins, Stewart and Vigoda8,Reference Helmuth, Jenssen and Perkins21] (or even the RC dynamics itself). Precise results characterising the distribution of
$\tilde{O}(n^2)$
by approximating the corresponding partition functions, by using, for example, the algorithms in [Reference Chen, Galanis, Goldberg, Perkins, Stewart and Vigoda8,Reference Helmuth, Jenssen and Perkins21] (or even the RC dynamics itself). Precise results characterising the distribution of
![]() $Q$
can further be found in [Reference Helmuth, Jenssen and Perkins21, Theorems 2 & 3]; it is shown for example that
$Q$
can further be found in [Reference Helmuth, Jenssen and Perkins21, Theorems 2 & 3]; it is shown for example that
![]() $Q$
converges to
$Q$
converges to
![]() $1/(q+1)$
as
$1/(q+1)$
as
![]() $q$
grows large.
$q$
grows large.
2.5 Organisation of the rest of the paper
We first give a summary of how to obtain our WSM results for the ordered phase in the next section (Section 3); this is the most involved part of our arguments. Then, in Section 4, we revisit the polymer framework for the random cluster model and show some technical results that we will need to carry out the WSM proofs in Sections 5 and 6 (for the ordered and disordered regimes, respectively). We conclude with Section 7 which has some left-over technical pieces needed for the proof of Theorem1. Appendix A has, for completeness, a proof of the mixing-time bound on the tree stated in Lemma9 (uses relatively standard arguments) and Appenbdix B reviews some standard monotonicity properties of the random cluster model.
3. Proof outline of the WSM within the ordered phase
3.1 Locally tree-like expanders
Analogously to [Reference Helmuth, Jenssen and Perkins21], we work a bit more generally with
![]() $\Delta$
-regular expanders, which are also tree-like. The expansion profile of an
$\Delta$
-regular expanders, which are also tree-like. The expansion profile of an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G=(V,E)$
for
$G=(V,E)$
for
![]() $\varepsilon \gt 0$
is given by
$\varepsilon \gt 0$
is given by
Then the classes
![]() $G_{\Delta, \delta }$
and
$G_{\Delta, \delta }$
and
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
are as follows.
${\mathcal{G}}_{\Delta, \delta, K}$
are as follows.
Definition 15.
Let
![]() $\Delta \geq 5$
be an integer, and
$\Delta \geq 5$
be an integer, and
![]() $\delta \in (0,1/2), K\gt 0$
be reals.
$\delta \in (0,1/2), K\gt 0$
be reals.
![]() $G_{\Delta, \delta }$
is the class of
$G_{\Delta, \delta }$
is the class of
![]() $\Delta$
-regular graphs such that
$\Delta$
-regular graphs such that
![]() $\phi _G(1/2) \geq 1/10$
and
$\phi _G(1/2) \geq 1/10$
and
![]() $\phi _G(\delta ) \geq 5/9$
.
$\phi _G(\delta ) \geq 5/9$
.
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
is the class of all locally
${\mathcal{G}}_{\Delta, \delta, K}$
is the class of all locally
![]() $K$
-treelike graphs
$K$
-treelike graphs
![]() $G\in{\mathcal{G}}_{\Delta, \delta }$
.
$G\in{\mathcal{G}}_{\Delta, \delta }$
.
We use the following lemma.
Lemma 16 ([Reference Helmuth, Jenssen and Perkins21, Proposition 37]). Fix
![]() $\Delta \geq 5$
. There is a constant
$\Delta \geq 5$
. There is a constant
![]() $\delta \in (0,1/2)$
such that w.h.p. a uniformly random
$\delta \in (0,1/2)$
such that w.h.p. a uniformly random
![]() $\Delta$
-regular graph belongs to
$\Delta$
-regular graph belongs to
![]() ${\mathcal{G}}_{\Delta, \delta }$
.
${\mathcal{G}}_{\Delta, \delta }$
.
Lemma16 and Lemma7 show that there is also a positive integer
![]() $K$
such that, w.h.p,
$K$
such that, w.h.p,
![]() $G\in \mathcal{G}_{\Delta, \delta, K}$
. Next we state an important property of expanders from [Reference Trevisan27].
$G\in \mathcal{G}_{\Delta, \delta, K}$
. Next we state an important property of expanders from [Reference Trevisan27].
Lemma 17 ([Reference Trevisan27, Lemma 2.3]). Let
![]() $G=(V,E)$
be a regular graph and consider
$G=(V,E)$
be a regular graph and consider
![]() $E'\subseteq E$
with
$E'\subseteq E$
with
![]() $|E'|\leq \theta |E|$
for some
$|E'|\leq \theta |E|$
for some
![]() $\theta \in (0,\phi _G(1/2))$
. Then
$\theta \in (0,\phi _G(1/2))$
. Then
![]() $(V,E\backslash E')$
has a component of size at least
$(V,E\backslash E')$
has a component of size at least
![]() $\big (1 - \tfrac{\theta }{2 \phi _G(1/2)}\big ) |V|$
.
$\big (1 - \tfrac{\theta }{2 \phi _G(1/2)}\big ) |V|$
.
We use Lemma17 to establish the existence of a giant component.
Definition 18.
The size of a component of a graph is the number of vertices in the component. A giant component in an
![]() $n$
-vertex graph is a component whose size is greater than
$n$
-vertex graph is a component whose size is greater than
![]() $n/2$
. Given a graph
$n/2$
. Given a graph
![]() $G=(V,E)$
and a subset
$G=(V,E)$
and a subset
![]() $F\subseteq E$
,
$F\subseteq E$
,
![]() $G[F]$
denotes the graph
$G[F]$
denotes the graph
![]() $(V,F)$
.
$(V,F)$
.
Definition 19.
Fix
![]() $\Delta \geq 5$
. Fix
$\Delta \geq 5$
. Fix
![]() $\delta \in (0,1/2)$
satisfying Lemma
16
. Let
$\delta \in (0,1/2)$
satisfying Lemma
16
. Let
![]() $\eta = \min (\delta /5, 1/100)$
.
$\eta = \min (\delta /5, 1/100)$
.
Corollary 20.
Fix integers
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K\geq 0$
and a real number
$K\geq 0$
and a real number
![]() $\delta \in (0,1/2)$
. Let
$\delta \in (0,1/2)$
. Let
![]() $G$
be a graph in
$G$
be a graph in
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
and let
${\mathcal{G}}_{\Delta, \delta, K}$
and let
![]() $\mathcal{F}$
be a configuration in
$\mathcal{F}$
be a configuration in
![]() $\Omega ^{\mathrm{ord}}$
or a partial configuration with
$\Omega ^{\mathrm{ord}}$
or a partial configuration with
![]() $|{\mathrm{In}}({\mathcal{F}})|\geq (1-\eta )|E|$
. Then there is a giant component in
$|{\mathrm{In}}({\mathcal{F}})|\geq (1-\eta )|E|$
. Then there is a giant component in
![]() $G[{\mathrm{In}}({\mathcal{F}})]$
whose size is at least
$G[{\mathrm{In}}({\mathcal{F}})]$
whose size is at least
![]() $ (1-\delta )|V|$
.
$ (1-\delta )|V|$
.
Proof. Apply Lemma17 with
![]() $E' = \mathrm{Out}({\mathcal{F}})$
and
$E' = \mathrm{Out}({\mathcal{F}})$
and
![]() $\theta = \eta = \min (\delta /5,1/100)$
. Note
$\theta = \eta = \min (\delta /5,1/100)$
. Note
![]() $|\mathrm{Out}({\mathcal{F}})|\leq \eta |E|$
and
$|\mathrm{Out}({\mathcal{F}})|\leq \eta |E|$
and
![]() $\phi _G(1/2)\geq 1/10$
. Thus the lemma say that
$\phi _G(1/2)\geq 1/10$
. Thus the lemma say that
![]() $G[{\mathrm{In}}({\mathcal{F}})]$
has a component of size at least
$G[{\mathrm{In}}({\mathcal{F}})]$
has a component of size at least
![]() $\left (1-\frac{\delta / 5}{2\cdot 1/10}\right )|V| = (1 - \delta )|V| \gt |V|/2$
.
$\left (1-\frac{\delta / 5}{2\cdot 1/10}\right )|V| = (1 - \delta )|V| \gt |V|/2$
.
3.2 Sketch of proof of Theorem5
Let
![]() $\Delta \geq 5$
be an integer. Consider any sufficiently large
$\Delta \geq 5$
be an integer. Consider any sufficiently large
![]() $q$
and any
$q$
and any
![]() $\beta \geq \beta _c$
. For sufficiently large
$\beta \geq \beta _c$
. For sufficiently large
![]() $n$
, choose a ‘radius’
$n$
, choose a ‘radius’
![]() $r \approx \tfrac{1}{\beta } \log n$
and let
$r \approx \tfrac{1}{\beta } \log n$
and let
![]() $G=(V,E)\sim{\mathcal{G}}_{n,\Delta }$
. Fix a vertex
$G=(V,E)\sim{\mathcal{G}}_{n,\Delta }$
. Fix a vertex
![]() $v\in V$
and an edge
$v\in V$
and an edge
![]() $e$
incident to
$e$
incident to
![]() $v$
. We wish to show, with sufficiently high probability, that
$v$
. We wish to show, with sufficiently high probability, that
![]() $\Vert{\pi _{{\mathcal{B}}_r^+(v)}(e \mapsto \cdot ) - \pi ^{{\mathrm{ord}}}_G(e\mapsto \cdot ) }\Vert _{\mathrm{TV}} \leq{1}/{(100 |E|)}$
.
$\Vert{\pi _{{\mathcal{B}}_r^+(v)}(e \mapsto \cdot ) - \pi ^{{\mathrm{ord}}}_G(e\mapsto \cdot ) }\Vert _{\mathrm{TV}} \leq{1}/{(100 |E|)}$
.
Our goal is essentially to construct a coupling of
![]() ${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}^+_{r}(v)}$
and
${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}^+_{r}(v)}$
and
![]() ${\mathcal{F}}^{\mathrm{ord}}\sim \pi ^{\mathrm{ord}}$
, such that
${\mathcal{F}}^{\mathrm{ord}}\sim \pi ^{\mathrm{ord}}$
, such that
![]() ${\mathbb{P}}({\mathcal{F}}^+(e)\neq{\mathcal{F}}^{\mathrm{ord}}(e))$
is sufficiently small. In order to construct the coupling, we take advantage of the fact that
${\mathbb{P}}({\mathcal{F}}^+(e)\neq{\mathcal{F}}^{\mathrm{ord}}(e))$
is sufficiently small. In order to construct the coupling, we take advantage of the fact that
![]() $G[B_r(v)]$
is locally tree-like. In fact, we identify a suitable subgraph of
$G[B_r(v)]$
is locally tree-like. In fact, we identify a suitable subgraph of
![]() $G[B_r(v)]$
without cycles and restrict the coupling to this subgraph.
$G[B_r(v)]$
without cycles and restrict the coupling to this subgraph.
Consider a breadth-first search from
![]() $v$
in
$v$
in
![]() $G[B_r(v)]$
. Let
$G[B_r(v)]$
. Let
![]() $T_0$
be the rooted tree consisting of all forward edges in this breadth-first search. All other edges in
$T_0$
be the rooted tree consisting of all forward edges in this breadth-first search. All other edges in
![]() $B_r(v)$
are called ‘excess edges’. W.h.p., since
$B_r(v)$
are called ‘excess edges’. W.h.p., since
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
, there are at most
$G\sim{\mathcal{G}}_{n,\Delta }$
, there are at most
![]() $K$
excess edges in
$K$
excess edges in
![]() $B_r(v)$
for some absolute constant
$B_r(v)$
for some absolute constant
![]() $K\gt 0$
. In particular, since
$K\gt 0$
. In particular, since
![]() $G$
is locally tree-like, we can identify integers
$G$
is locally tree-like, we can identify integers
![]() $r_1$
and
$r_1$
and
![]() $r_2$
satisfying
$r_2$
satisfying
![]() $r \geq r_1 \gt r_2 \geq 0$
such that
$r \geq r_1 \gt r_2 \geq 0$
such that
![]() $E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
contains no excess edges and
$E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
contains no excess edges and
![]() $r_1 - r_2 \geq r/(2K)=\Omega (r)$
. The fact that
$r_1 - r_2 \geq r/(2K)=\Omega (r)$
. The fact that
![]() $r_1-r_2 = \Omega (r)$
ensures that
$r_1-r_2 = \Omega (r)$
ensures that
![]() $B_{r_1}(v) \setminus B_{r_2}(v)$
is a sufficiently large subgraph of
$B_{r_1}(v) \setminus B_{r_2}(v)$
is a sufficiently large subgraph of
![]() $G$
, and the coupling focuses on this subgraph.
$G$
, and the coupling focuses on this subgraph.
In order to describe the coupling process we need a small amount of notation. A partial configuration
![]() $\mathcal{F}$
is a map from the edges of
$\mathcal{F}$
is a map from the edges of
![]() $G$
to the set
$G$
to the set
![]() $\{0,1,*\}$
. In-edges and out-edges (those that are mapped to
$\{0,1,*\}$
. In-edges and out-edges (those that are mapped to
![]() $1$
or to
$1$
or to
![]() $0$
) are ‘revealed’ and edges that are mapped to
$0$
) are ‘revealed’ and edges that are mapped to
![]() $*$
are ‘unrevealed’. A refinement of a partial configuration is obtained by revealing more edges. We use
$*$
are ‘unrevealed’. A refinement of a partial configuration is obtained by revealing more edges. We use
![]() ${\mathcal{F}} \subseteq{\mathcal{F}}'$
to denote the fact that
${\mathcal{F}} \subseteq{\mathcal{F}}'$
to denote the fact that
![]() ${\mathcal{F}}'$
refines
${\mathcal{F}}'$
refines
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
In the coupling, we generate a sequence of edge subsets
![]() $F_0 \subseteq F_1 \subseteq \cdots \subseteq E$
such that, after iteration
$F_0 \subseteq F_1 \subseteq \cdots \subseteq E$
such that, after iteration
![]() $i$
, the edges in
$i$
, the edges in
![]() $F_i$
are revealed. We also construct two sequences of partial configurations
$F_i$
are revealed. We also construct two sequences of partial configurations
![]() ${\mathcal{F}}_0^+\subseteq{\mathcal{F}}_1^+\subseteq \dots \subseteq{\mathcal{F}}^+$
and
${\mathcal{F}}_0^+\subseteq{\mathcal{F}}_1^+\subseteq \dots \subseteq{\mathcal{F}}^+$
and
![]() ${\mathcal{F}}_0^{\mathrm{ord}}\subseteq{\mathcal{F}}_1^{\mathrm{ord}}\subseteq \dots \subseteq{\mathcal{F}}^{\mathrm{ord}}$
, maintaining the invariant that the revealed edges in
${\mathcal{F}}_0^{\mathrm{ord}}\subseteq{\mathcal{F}}_1^{\mathrm{ord}}\subseteq \dots \subseteq{\mathcal{F}}^{\mathrm{ord}}$
, maintaining the invariant that the revealed edges in
![]() ${\mathcal{F}}_i^{\mathrm{ord}}$
and
${\mathcal{F}}_i^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}_i^+$
are exactly the edges in
${\mathcal{F}}_i^+$
are exactly the edges in
![]() $F_i$
. The coupling will have the crucial property that
$F_i$
. The coupling will have the crucial property that
![]() ${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+ \sim \pi _{{\mathcal{B}}_{r_1}^+(v)}$
${\mathcal{F}}^+ \sim \pi _{{\mathcal{B}}_{r_1}^+(v)}$
-
• The process starts with iteration
 $i=0$
. The initial set
$i=0$
. The initial set
 $F_0$
of revealed edges is all edges except those in
$F_0$
of revealed edges is all edges except those in
 $E(B_{r_1}(v))$
. In
$E(B_{r_1}(v))$
. In
 ${\mathcal{F}}_0^{\mathrm{ord}}$
these revealed edges are sampled from the projection
${\mathcal{F}}_0^{\mathrm{ord}}$
these revealed edges are sampled from the projection
 $\pi ^{\mathrm{ord}}_{F_0}$
of
$\pi ^{\mathrm{ord}}_{F_0}$
of
 $\pi ^{\mathrm{ord}}$
onto
$\pi ^{\mathrm{ord}}$
onto
 $F_0$
. It is likely that the configuration
$F_0$
. It is likely that the configuration
 ${\mathcal{F}}_0^{\mathrm{ord}}$
has at least
${\mathcal{F}}_0^{\mathrm{ord}}$
has at least
 $(1-\eta )|E|$
in-edges. If not, then the coupling terminates (unsuccessfully), generating
$(1-\eta )|E|$
in-edges. If not, then the coupling terminates (unsuccessfully), generating
 ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
 ${\mathcal{F}}^+$
from the right distributions. We will show that the probability of this unsuccessful termination is low. On the other hand, if
${\mathcal{F}}^+$
from the right distributions. We will show that the probability of this unsuccessful termination is low. On the other hand, if
 ${\mathcal{F}}_0^{\mathrm{ord}}$
has a least
${\mathcal{F}}_0^{\mathrm{ord}}$
has a least
 $(1-\eta )|E|$
in-edges, then we are off to a good start. All configurations refining
$(1-\eta )|E|$
in-edges, then we are off to a good start. All configurations refining
 ${\mathcal{F}}_0^{\mathrm{ord}}$
are in
${\mathcal{F}}_0^{\mathrm{ord}}$
are in
 $\Omega ^{\mathrm{ord}}$
, so the projection of
$\Omega ^{\mathrm{ord}}$
, so the projection of
 $\pi$
and
$\pi$
and
 $\pi ^{\mathrm{ord}}$
onto subsequent edges that get revealed are the same (making it easier to continue the coupling). At this point
$\pi ^{\mathrm{ord}}$
onto subsequent edges that get revealed are the same (making it easier to continue the coupling). At this point
 ${\mathcal{F}}_0^+$
is taken to be the configuration with revealed edges
${\mathcal{F}}_0^+$
is taken to be the configuration with revealed edges
 $F_0$
where all revealed edges are in-edges.
$F_0$
where all revealed edges are in-edges. -
• After iteration
 $i=0$
, iterations continue with
$i=0$
, iterations continue with
 $i=1,2,\ldots$
until an edge is revealed whose distance from
$i=1,2,\ldots$
until an edge is revealed whose distance from
 $v$
is at most
$v$
is at most
 $r_2$
or until the in-edges in
$r_2$
or until the in-edges in
 ${\mathcal{F}}_i^{\mathrm{ord}}$
induce a giant component, and this giant component contains all vertices on the boundary of
${\mathcal{F}}_i^{\mathrm{ord}}$
induce a giant component, and this giant component contains all vertices on the boundary of
 $F_i$
. We will show that it is very unlikely that an edge at distance at most
$F_i$
. We will show that it is very unlikely that an edge at distance at most
 $r_2$
from
$r_2$
from
 $v$
is reached. So it is likely the giant component in
$v$
is reached. So it is likely the giant component in
 ${\mathcal{F}}_i^{\mathrm{ord}}$
contains all vertices on the boundary of
${\mathcal{F}}_i^{\mathrm{ord}}$
contains all vertices on the boundary of
 $F_i$
. This is a good situation because the conditional distribution of
$F_i$
. This is a good situation because the conditional distribution of
 $\pi$
, conditioned on refining
$\pi$
, conditioned on refining
 ${\mathcal{F}}_i^{\mathrm{ord}}$
and the conditional distribution of
${\mathcal{F}}_i^{\mathrm{ord}}$
and the conditional distribution of
 ${\mathcal{F}}^+$
, conditioned on refining
${\mathcal{F}}^+$
, conditioned on refining
 ${\mathcal{F}}_i^+$
induce the same distribution on edges incident to
${\mathcal{F}}_i^+$
induce the same distribution on edges incident to
 $v$
, which enables us to show that
$v$
, which enables us to show that
 ${\mathbb{P}}({\mathcal{F}}^+(e)\neq{\mathcal{F}}^{\mathrm{ord}}(e))$
is sufficiently small.
${\mathbb{P}}({\mathcal{F}}^+(e)\neq{\mathcal{F}}^{\mathrm{ord}}(e))$
is sufficiently small. -
• The process at iteration
 $i+1$
is as follows.
$i+1$
is as follows.
 $W_i$
is taken to be the set of all vertices on the boundary of
$W_i$
is taken to be the set of all vertices on the boundary of
 $F_i$
whose components (induced by the in-edges in
$F_i$
whose components (induced by the in-edges in
 ${\mathcal{F}}_i^{\mathrm{ord}}$
) are all small. By ‘boundary’. we mean that vertices in
${\mathcal{F}}_i^{\mathrm{ord}}$
) are all small. By ‘boundary’. we mean that vertices in
 $W_i$
are adjacent to revealed edges, and to unrevealed edges. If
$W_i$
are adjacent to revealed edges, and to unrevealed edges. If
 $W_i$
is empty, then the coupling finishes. Otherwise, a vertex
$W_i$
is empty, then the coupling finishes. Otherwise, a vertex
 $w_i\in W_i$
is chosen to be as far from
$w_i\in W_i$
is chosen to be as far from
 $v$
as possible. The edges in the subtree of
$v$
as possible. The edges in the subtree of
 $T_0$
below the parent of
$T_0$
below the parent of
 $w_i$
are revealed in
$w_i$
are revealed in
 $F_{i+1}$
.
$F_{i+1}$
.
The main remaining ingredient in the proof is showing that the unsuccessful terminations of the coupling are unlikely. To do this, we use the polymer framework of [Reference Helmuth, Jenssen and Perkins21]. (Ordered) polymers are defined using an inductive definition. For a set of edges
![]() $A\subseteq E$
, let
$A\subseteq E$
, let
![]() ${\mathcal{B}}_0(A) = A$
, and inductively for
${\mathcal{B}}_0(A) = A$
, and inductively for
![]() $j = 0,1,2,\dots$
define
$j = 0,1,2,\dots$
define
![]() ${\mathcal{B}}_{j+1}(A)$
to be the set of all edges such that they are either in
${\mathcal{B}}_{j+1}(A)$
to be the set of all edges such that they are either in
![]() ${\mathcal{B}}_j(A)$
or edges that are incident to a vertex that has at least
${\mathcal{B}}_j(A)$
or edges that are incident to a vertex that has at least
![]() ${5\Delta }/{9}$
incident edges in
${5\Delta }/{9}$
incident edges in
![]() ${\mathcal{B}}_j(A)$
. Let
${\mathcal{B}}_j(A)$
. Let
![]() ${\mathcal{B}}_\infty (A) = \bigcup _{j\in \mathbb{N}}{\mathcal{B}}_j(A)$
. An ordered polymer of a configuration
${\mathcal{B}}_\infty (A) = \bigcup _{j\in \mathbb{N}}{\mathcal{B}}_j(A)$
. An ordered polymer of a configuration
![]() $\mathcal{F}$
is a connected component of
$\mathcal{F}$
is a connected component of
![]() $B_\infty (\mathrm{Out}({\mathcal{F}}))$
. The bulk of the work is to prove the following lemma, which is repeated in Section 5.2 (with more detail) as Lemma44.
$B_\infty (\mathrm{Out}({\mathcal{F}}))$
. The bulk of the work is to prove the following lemma, which is repeated in Section 5.2 (with more detail) as Lemma44.
Lemma 21.
Fix
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K, M\gt 0$
. Suppose that
$K, M\gt 0$
. Suppose that
![]() $\beta \geq 3 M$
. Suppose that
$\beta \geq 3 M$
. Suppose that
![]() $n$
is sufficiently large so that
$n$
is sufficiently large so that
![]() $r\;:\!=\; \tfrac{M}\beta \log _{\Delta -1} n \gt K$
and
$r\;:\!=\; \tfrac{M}\beta \log _{\Delta -1} n \gt K$
and
![]() $|B_{r}(v)| \leq 9 \Delta n/200$
. Define
$|B_{r}(v)| \leq 9 \Delta n/200$
. Define
![]() $r_1$
as above. Let
$r_1$
as above. Let
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
be generated by the process. Then at least one of the following conditions holds.
${\mathcal{F}}^+$
be generated by the process. Then at least one of the following conditions holds.
-
1.
 ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
 ${\mathcal{F}}^+$
agree on the edges that are incident to
${\mathcal{F}}^+$
agree on the edges that are incident to
 $v$
.
$v$
. -
2.
 $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus E(B_{r_1}(v))| \lt (1-\eta ) |E|$
.
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus E(B_{r_1}(v))| \lt (1-\eta ) |E|$
. -
3.
 ${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
 $\frac{r}{400\Delta (1+K)}-1$
.
$\frac{r}{400\Delta (1+K)}-1$
.
To complete the proof of Theorem5, we show that items 2 and 3 are unlikely. The proof that item 2 is unlikely, Lemma45, follows from the slack specified in Equation (2) of Lemma3. The proof that item 3 is unlikely, Lemma28, follows from an analysis on the size of polymers by adapting appropriately the cluster expansion techniques of [Reference Helmuth, Jenssen and Perkins21] (a bit of extra work is needed there to capture the
![]() $1/\beta$
dependence in the size of the polymer, see Lemma28).
$1/\beta$
dependence in the size of the polymer, see Lemma28).
The proof of WSM for the disordered phase (Theorem6) follows a similar strategy but the details are substantially simpler (due to a more straightforward notion of polymers), the argument can be found in Section 6.
4. Polymers for RC on expander graphs
All logarithms in this paper are with base
![]() $\mathrm{e}$
. Given a graph
$\mathrm{e}$
. Given a graph
![]() $G=(V,E)$
, a subset
$G=(V,E)$
, a subset
![]() $U\subseteq V$
and a subset
$U\subseteq V$
and a subset
![]() $F\subseteq E$
, we use
$F\subseteq E$
, we use
![]() $G[U]$
to denote the subgraph of
$G[U]$
to denote the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $U$
and we use
$U$
and we use
![]() $G[F]$
to denote the graph
$G[F]$
to denote the graph
![]() $(V,F)$
.
$(V,F)$
.
4.1 The RC model on expanders in the ordered regime
We use the following Lemma from [Reference Helmuth, Jenssen and Perkins21].
Lemma 22 ([Reference Helmuth, Jenssen and Perkins21, Lemma 8]). Let
![]() $\Delta \geq 5$
,
$\Delta \geq 5$
,
![]() $\delta \in (0, 1/2)$
, and
$\delta \in (0, 1/2)$
, and
![]() $\zeta \in (0, 1/2)$
be reals. Suppose that
$\zeta \in (0, 1/2)$
be reals. Suppose that
![]() $G=(V,E)\in{\mathcal{G}}_{\Delta, \delta }$
satisfies
$G=(V,E)\in{\mathcal{G}}_{\Delta, \delta }$
satisfies
![]() $|V|\geq 360/(\zeta \delta )$
and
$|V|\geq 360/(\zeta \delta )$
and
![]() $A\subset E$
is such that
$A\subset E$
is such that
![]() $\zeta |E| \leq |A| \leq (1-\zeta )|E|$
. Then
$\zeta |E| \leq |A| \leq (1-\zeta )|E|$
. Then
![]() ${c(A)}/{|V|} +{|A|}/{|E|} \leq 1 - \zeta /40$
where
${c(A)}/{|V|} +{|A|}/{|E|} \leq 1 - \zeta /40$
where
![]() $c(A)$
is the number of connected components in
$c(A)$
is the number of connected components in
![]() $G[A]$
.
$G[A]$
.
Remark 23 (Reference Helmuth, Jenssen and Perkins21, Lemma 8). is proved for the special case of
![]() $\zeta = \min (1/100,\delta /5)$
, however the proof works for any positive
$\zeta = \min (1/100,\delta /5)$
, however the proof works for any positive
![]() $\zeta \lt 1/2$
.
$\zeta \lt 1/2$
.
Lemma 24 ([Reference Helmuth, Jenssen and Perkins21, Theorems 1 and 2]). Let
![]() $\Delta \geq 5$
be an integer. Fix
$\Delta \geq 5$
be an integer. Fix
![]() $\delta \in (0,1/2)$
satisfying Lemma
16
. Let
$\delta \in (0,1/2)$
satisfying Lemma
16
. Let
![]() $\eta = \min \{\delta /5,1/100\}$
. Let
$\eta = \min \{\delta /5,1/100\}$
. Let
![]() $q_0 \geq e^{21 \Delta /\eta }$
be sufficiently large that Theorems1 and 2 of [21] hold. There is a positive number
$q_0 \geq e^{21 \Delta /\eta }$
be sufficiently large that Theorems1 and 2 of [21] hold. There is a positive number
![]() $\zeta \lt \eta$
such that w.h.p. for
$\zeta \lt \eta$
such that w.h.p. for
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
, it holds that
$G\sim{\mathcal{G}}_{n,\Delta }$
, it holds that
 \begin{equation*} \begin {aligned} \mbox {for $\beta \geq \beta _c$}, &\quad \pi _G^{\mathrm {ord}}\Big (|{\mathrm {In}}({\mathcal {F}})|\leq (1-\zeta )|E|\Big )=\mathrm {e}^{-\Omega (n)},\\[5pt] \mbox {for $\beta \leq \beta _c$}, &\quad \pi _G^{\mathrm {dis}}\Big (|{\mathrm {In}}({\mathcal {F}})|\geq \zeta |E|\Big )=\mathrm {e}^{-\Omega (n)}. \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} \mbox {for $\beta \geq \beta _c$}, &\quad \pi _G^{\mathrm {ord}}\Big (|{\mathrm {In}}({\mathcal {F}})|\leq (1-\zeta )|E|\Big )=\mathrm {e}^{-\Omega (n)},\\[5pt] \mbox {for $\beta \leq \beta _c$}, &\quad \pi _G^{\mathrm {dis}}\Big (|{\mathrm {In}}({\mathcal {F}})|\geq \zeta |E|\Big )=\mathrm {e}^{-\Omega (n)}. \end {aligned} \end{equation*}
Proof. We prove the first bound, the second is similar. Choose
![]() $\zeta = 20 \Delta /\log (q_0)$
. Note that
$\zeta = 20 \Delta /\log (q_0)$
. Note that
![]() $\zeta \lt \eta$
, as desired. Let
$\zeta \lt \eta$
, as desired. Let
![]() $\Omega ' = \{{\mathcal{F}} \in \Omega ^{\mathrm{ord}}\;:\; |{\mathrm{In}}({\mathcal{F}})|\leq (1-\zeta )|E|\}$
and let
$\Omega ' = \{{\mathcal{F}} \in \Omega ^{\mathrm{ord}}\;:\; |{\mathrm{In}}({\mathcal{F}})|\leq (1-\zeta )|E|\}$
and let
Let
![]() $z = \max \{q,(\mathrm{e}^{\beta }-1)^{\Delta /2}\}$
. Since
$z = \max \{q,(\mathrm{e}^{\beta }-1)^{\Delta /2}\}$
. Since
![]() $Z \geq z^n$
every
$Z \geq z^n$
every
![]() ${\mathcal{F}}\in \Omega$
has
${\mathcal{F}}\in \Omega$
has
Since
![]() $\zeta \lt \eta \lt 1/2$
, for any
$\zeta \lt \eta \lt 1/2$
, for any
![]() ${\mathcal{F}}\in \Omega '$
,
${\mathcal{F}}\in \Omega '$
,
![]() $\zeta |E| \leq (1-\eta )|E| \leq |{\mathrm{In}}({\mathcal{F}})| \leq (1-\zeta )|E|$
. By Lemma16, w.h.p.,
$\zeta |E| \leq (1-\eta )|E| \leq |{\mathrm{In}}({\mathcal{F}})| \leq (1-\zeta )|E|$
. By Lemma16, w.h.p.,
![]() $G\in \mathcal{G}_{\Delta, \delta }$
. By Lemma22, for
$G\in \mathcal{G}_{\Delta, \delta }$
. By Lemma22, for
![]() $n\geq 360/(\zeta \delta )$
, we have
$n\geq 360/(\zeta \delta )$
, we have
![]() $c({\mathcal{F}})/n + |{\mathrm{In}}({\mathcal{F}})|/|E| \leq 1-\zeta /40$
so
$c({\mathcal{F}})/n + |{\mathrm{In}}({\mathcal{F}})|/|E| \leq 1-\zeta /40$
so
![]() $Z'/Z \leq 2^{n\Delta /2} z^{n(-\zeta /40)}$
, which gives
$Z'/Z \leq 2^{n\Delta /2} z^{n(-\zeta /40)}$
, which gives
![]() $Z'/Z = \mathrm{e}^{-\Omega (n)}$
since
$Z'/Z = \mathrm{e}^{-\Omega (n)}$
since
![]() $q \gt \mathrm{e}^{20 \Delta /\zeta }$
. To finish, we will show that
$q \gt \mathrm{e}^{20 \Delta /\zeta }$
. To finish, we will show that
![]() $Z/Z^{\mathrm{ord}} = O(1)$
, so that
$Z/Z^{\mathrm{ord}} = O(1)$
, so that
![]() $\frac{Z'}{Z^{\mathrm{ord}}} = \frac{Z'}{Z} \times \frac{Z}{Z^{\mathrm{ord}}} = \mathrm{e}^{-\Omega (n)} O(1) = \mathrm{e}^{-\Omega (n)}$
. If
$\frac{Z'}{Z^{\mathrm{ord}}} = \frac{Z'}{Z} \times \frac{Z}{Z^{\mathrm{ord}}} = \mathrm{e}^{-\Omega (n)} O(1) = \mathrm{e}^{-\Omega (n)}$
. If
![]() $\beta \gt \beta _c$
, item 3 of [Reference Helmuth, Jenssen and Perkins21, Theorem1] says that there are positive numbers
$\beta \gt \beta _c$
, item 3 of [Reference Helmuth, Jenssen and Perkins21, Theorem1] says that there are positive numbers
![]() $n_0$
and
$n_0$
and
![]() $\xi$
such that, for
$\xi$
such that, for
![]() $n\geq n_0$
,
$n\geq n_0$
,
![]() $(1/n) \log ((Z-Z^{\mathrm{ord}})/Z) \leq -\xi$
. So for
$(1/n) \log ((Z-Z^{\mathrm{ord}})/Z) \leq -\xi$
. So for
![]() $n\geq n_0$
,
$n\geq n_0$
,
![]() $Z^{\mathrm{ord}}/Z \geq 1 - e^{-\xi n}$
, which is at least
$Z^{\mathrm{ord}}/Z \geq 1 - e^{-\xi n}$
, which is at least
![]() $1/2$
for
$1/2$
for
![]() $n\geq 1/\xi$
. If
$n\geq 1/\xi$
. If
![]() $\beta = \beta _c$
, then items 1 and 3 of [Reference Helmuth, Jenssen and Perkins21, Theorem 2] show that
$\beta = \beta _c$
, then items 1 and 3 of [Reference Helmuth, Jenssen and Perkins21, Theorem 2] show that
![]() $Z^{\mathrm{ord}}/Z$
converges in distribution to a random variable
$Z^{\mathrm{ord}}/Z$
converges in distribution to a random variable
![]() $Q/(Q+1)$
where (say)
$Q/(Q+1)$
where (say)
![]() $Q\geq q/2$
for
$Q\geq q/2$
for
![]() $q\geq q_0$
. So for sufficiently large
$q\geq q_0$
. So for sufficiently large
![]() $q$
,
$q$
,
![]() $Z^{\mathrm{ord}}/Z = O(1)$
.
$Z^{\mathrm{ord}}/Z = O(1)$
.
4.2 Disordered polymers
We will use disordered polymers from [Reference Helmuth, Jenssen and Perkins21, Section 2.3]. Given a graph
![]() $G = (V,E)$
and a configuration
$G = (V,E)$
and a configuration
![]() ${\mathcal{F}}\in \Omega ^{\mathrm{dis}}$
, a disordered polymer of
${\mathcal{F}}\in \Omega ^{\mathrm{dis}}$
, a disordered polymer of
![]() $\mathcal{F}$
is a connected component of
$\mathcal{F}$
is a connected component of
![]() $G[{\mathrm{In}}({\mathcal{F}})]$
. Since
$G[{\mathrm{In}}({\mathcal{F}})]$
. Since
![]() ${\mathcal{F}} \in \Omega ^{\mathrm{dis}}$
, each such connected component contains at most
${\mathcal{F}} \in \Omega ^{\mathrm{dis}}$
, each such connected component contains at most
![]() $\eta |E|$
edges.
$\eta |E|$
edges.
Each disordered polymer
![]() $\gamma =(V(\gamma ),E(\gamma ))$
has an associated weight given by
$\gamma =(V(\gamma ),E(\gamma ))$
has an associated weight given by
![]() $ w_\gamma ^{\mathrm{dis}} \;:\!=\; q^{1-|V(\gamma )|} (e^{\beta }-1)^{|E(\gamma )|}$
. We observe the following relation between the weight of a disordered configuration and the weights of its polymers.
$ w_\gamma ^{\mathrm{dis}} \;:\!=\; q^{1-|V(\gamma )|} (e^{\beta }-1)^{|E(\gamma )|}$
. We observe the following relation between the weight of a disordered configuration and the weights of its polymers.
Observation 25.
For
![]() ${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
, let
${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
, let
![]() $\Gamma ^{\mathrm{dis}}({\mathcal{F}})$
be the set of disordered polymers of
$\Gamma ^{\mathrm{dis}}({\mathcal{F}})$
be the set of disordered polymers of
![]() $\mathcal{F}$
. Then
$\mathcal{F}$
. Then
This observation follows from the fact each vertex of
![]() $G$
is contained in some polymer of
$G$
is contained in some polymer of
![]() $\mathcal{F}$
, each in-edge of
$\mathcal{F}$
, each in-edge of
![]() $\mathcal{F}$
is an edge of some polymer of
$\mathcal{F}$
is an edge of some polymer of
![]() $\mathcal{F}$
, and each polymer of
$\mathcal{F}$
, and each polymer of
![]() $\mathcal{F}$
corresponds to one component of
$\mathcal{F}$
corresponds to one component of
![]() $G[{\mathrm{In}}({\mathcal{F}})]$
.
$G[{\mathrm{In}}({\mathcal{F}})]$
.
Based on the work by Helmuth, Jenssen and Perkins [Reference Helmuth, Jenssen and Perkins21, Proposition 11], we can upper bound the probability that
![]() ${\mathcal{F}}\sim \pi ^{\mathrm{dis}}$
contains a large polymer.
${\mathcal{F}}\sim \pi ^{\mathrm{dis}}$
contains a large polymer.
Lemma 26.
Let
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K\geq 0$
be integers,
$K\geq 0$
be integers,
![]() $\delta \in (0, 1/2)$
be real. Let
$\delta \in (0, 1/2)$
be real. Let
![]() $C$
be a constant. Then, for all sufficiently large
$C$
be a constant. Then, for all sufficiently large
![]() $q$
, the following holds for all
$q$
, the following holds for all
![]() $\beta \leq \log (q^{2.1/\Delta }+1)$
. Let
$\beta \leq \log (q^{2.1/\Delta }+1)$
. Let
![]() $n$
be sufficiently large. For
$n$
be sufficiently large. For
![]() $G\in{\mathcal{G}}_{\Delta, \delta, K}$
with
$G\in{\mathcal{G}}_{\Delta, \delta, K}$
with
![]() $n=|V(G)|$
, for
$n=|V(G)|$
, for
![]() $s\;:\!=\;C \log n$
,
$s\;:\!=\;C \log n$
,
Proof. Let
![]() $q$
and
$q$
and
![]() $n$
be large enough so that Proposition 11 from [Reference Helmuth, Jenssen and Perkins21] applies, and so in particular [Reference Helmuth, Jenssen and Perkins21, Equation (13)] holds, and also that
$n$
be large enough so that Proposition 11 from [Reference Helmuth, Jenssen and Perkins21] applies, and so in particular [Reference Helmuth, Jenssen and Perkins21, Equation (13)] holds, and also that
![]() $s \gt 1$
and
$s \gt 1$
and
![]() $q\geq e^{4\Delta (\frac{5}{2C}-1)}$
.
$q\geq e^{4\Delta (\frac{5}{2C}-1)}$
.
For a disordered configuration
![]() $\mathcal{F}$
, let
$\mathcal{F}$
, let
![]() $\Gamma ^{\mathrm{dis}}({\mathcal{F}})$
be the set of disordered polymers of
$\Gamma ^{\mathrm{dis}}({\mathcal{F}})$
be the set of disordered polymers of
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
First we will bound, for a particular polymer
![]() $\gamma$
with
$\gamma$
with
![]() $|E(\gamma )| \geq 1$
,
$|E(\gamma )| \geq 1$
,
![]() ${\mathbb{P}}(\gamma \in \Gamma ^{\mathrm{dis}}(.))$
. Suppose
${\mathbb{P}}(\gamma \in \Gamma ^{\mathrm{dis}}(.))$
. Suppose
![]() ${\mathcal{F}}\in \Omega ^{\mathrm{dis}}$
has
${\mathcal{F}}\in \Omega ^{\mathrm{dis}}$
has
![]() $\gamma \in \Gamma ^{\mathrm{dis}}({\mathcal{F}})$
. By Observation25,
$\gamma \in \Gamma ^{\mathrm{dis}}({\mathcal{F}})$
. By Observation25,
![]() $w_G({\mathcal{F}}) = q^n \prod _{\gamma \in \Gamma ^{\mathrm{dis}}({\mathcal{F}})} w_\gamma ^{\mathrm{dis}}$
. Let
$w_G({\mathcal{F}}) = q^n \prod _{\gamma \in \Gamma ^{\mathrm{dis}}({\mathcal{F}})} w_\gamma ^{\mathrm{dis}}$
. Let
![]() ${\mathcal{F}}'$
be the (disordered) configuration defined by
${\mathcal{F}}'$
be the (disordered) configuration defined by
![]() ${\mathrm{In}}({\mathcal{F}}') ={\mathrm{In}}({\mathcal{F}})\backslash E(\gamma )$
. Since
${\mathrm{In}}({\mathcal{F}}') ={\mathrm{In}}({\mathcal{F}})\backslash E(\gamma )$
. Since
![]() $E(\gamma )\neq \emptyset$
,
$E(\gamma )\neq \emptyset$
,
![]() ${\mathcal{F}}\neq{\mathcal{F}}'$
. By construction,
${\mathcal{F}}\neq{\mathcal{F}}'$
. By construction,
![]() ${\mathcal{F}}'\in \Omega ^{\mathrm{dis}}$
. Since vertices in
${\mathcal{F}}'\in \Omega ^{\mathrm{dis}}$
. Since vertices in
![]() $\gamma$
are not incident to edges in
$\gamma$
are not incident to edges in
![]() ${\mathrm{In}}({\mathcal{F}}')$
,
${\mathrm{In}}({\mathcal{F}}')$
,
![]() $\Gamma ^{\mathrm{dis}}({\mathcal{F}}') = (\Gamma ^{\mathrm{dis}}({\mathcal{F}})\setminus \{\gamma \})\cup _{v\in \gamma } \{v\}$
. A polymer
$\Gamma ^{\mathrm{dis}}({\mathcal{F}}') = (\Gamma ^{\mathrm{dis}}({\mathcal{F}})\setminus \{\gamma \})\cup _{v\in \gamma } \{v\}$
. A polymer
![]() $\gamma '$
consisting of a single vertex has weight
$\gamma '$
consisting of a single vertex has weight
![]() $w_{\gamma '}^{\mathrm{dis}} = 1$
. Thus,
$w_{\gamma '}^{\mathrm{dis}} = 1$
. Thus,
![]() $w_G({\mathcal{F}}') = w_G({\mathcal{F}})/w_\gamma ^{\mathrm{dis}}$
. Let
$w_G({\mathcal{F}}') = w_G({\mathcal{F}})/w_\gamma ^{\mathrm{dis}}$
. Let
![]() $\Omega _\gamma$
be the set of all disordered configurations containing
$\Omega _\gamma$
be the set of all disordered configurations containing
![]() $\gamma$
as a polymer. Then
$\gamma$
as a polymer. Then
![]() $Z^{\mathrm{dis}} \geq \sum _{{\mathcal{F}}\in \Omega _\gamma } (w_G({\mathcal{F}}) + w_G({\mathcal{F}}')) = (1 + 1/w_\gamma ^{\mathrm{dis}})\sum _{{\mathcal{F}}\in \Omega _\gamma } w_G({\mathcal{F}})$
. Thus, the probability that
$Z^{\mathrm{dis}} \geq \sum _{{\mathcal{F}}\in \Omega _\gamma } (w_G({\mathcal{F}}) + w_G({\mathcal{F}}')) = (1 + 1/w_\gamma ^{\mathrm{dis}})\sum _{{\mathcal{F}}\in \Omega _\gamma } w_G({\mathcal{F}})$
. Thus, the probability that
![]() ${\mathcal{F}}\sim \pi ^{\mathrm{dis}}$
contains the polymer
${\mathcal{F}}\sim \pi ^{\mathrm{dis}}$
contains the polymer
![]() $\gamma$
is at most
$\gamma$
is at most
![]() $\frac{1}{1 + 1/w_\gamma ^{\mathrm{dis}}} \leq w_\gamma ^{\mathrm{dis}}$
.
$\frac{1}{1 + 1/w_\gamma ^{\mathrm{dis}}} \leq w_\gamma ^{\mathrm{dis}}$
.
Next, for
![]() $v\in V(G)$
let
$v\in V(G)$
let
![]() $p_v$
be the probability that
$p_v$
be the probability that
![]() ${\mathcal{F}}\sim \pi _G^{\mathrm{dis}}$
has a polymer with at least
${\mathcal{F}}\sim \pi _G^{\mathrm{dis}}$
has a polymer with at least
![]() $s$
edges containing the vertex
$s$
edges containing the vertex
![]() $v$
vertex
$v$
vertex
![]() $v$
. By a union bound,
$v$
. By a union bound,
![]() $p_v \leq P_v \;:\!=\; \sum _{\gamma \ni v: |E(\gamma )|\geq s} w_\gamma ^{\mathrm{dis}}$
. Let
$p_v \leq P_v \;:\!=\; \sum _{\gamma \ni v: |E(\gamma )|\geq s} w_\gamma ^{\mathrm{dis}}$
. Let
![]() $\theta = \log (q)/(4 \Delta )$
. By [Reference Helmuth, Jenssen and Perkins21, Equation (13)],
$\theta = \log (q)/(4 \Delta )$
. By [Reference Helmuth, Jenssen and Perkins21, Equation (13)],
Thus also
Hence
![]() $P_v \leq (1/2) e^{-(1+\theta )s}$
. By a union bound over all vertices, the probability in the statement of the lemma is at most
$P_v \leq (1/2) e^{-(1+\theta )s}$
. By a union bound over all vertices, the probability in the statement of the lemma is at most
![]() $\sum _v P_v \leq (n/2) 2^{-(1+\theta )s}= (1/2) n^{1-C(1+\theta )}$
. The lemma follows by requiring
$\sum _v P_v \leq (n/2) 2^{-(1+\theta )s}= (1/2) n^{1-C(1+\theta )}$
. The lemma follows by requiring
![]() $q$
to be sufficiently large with respect to
$q$
to be sufficiently large with respect to
![]() $\Delta$
and
$\Delta$
and
![]() $C$
that
$C$
that
![]() $C(1+\theta ) -1 \geq 3/2$
.
$C(1+\theta ) -1 \geq 3/2$
.
4.3 Ordered polymers
We use the definition of ordered polymers from [Reference Helmuth, Jenssen and Perkins21, Section 2.4.2]. Let
![]() $G=(V,E)$
be a graph of max degree
$G=(V,E)$
be a graph of max degree
![]() $\Delta$
with
$\Delta$
with
![]() $n=|V(G)|$
and
$n=|V(G)|$
and
![]() $m=|E(G)|$
. For a set of edges
$m=|E(G)|$
. For a set of edges
![]() $A\subseteq E$
, Let
$A\subseteq E$
, Let
![]() ${\mathcal{B}}_0(A) = A$
, and inductively for
${\mathcal{B}}_0(A) = A$
, and inductively for
![]() $i = 0,1,2,\dots$
define
$i = 0,1,2,\dots$
define
![]() ${\mathcal{B}}_{i+1}(A)$
to be the set of all edges such that they are either in
${\mathcal{B}}_{i+1}(A)$
to be the set of all edges such that they are either in
![]() ${\mathcal{B}}_i(A)$
or edges that are incident to a vertex that has at least
${\mathcal{B}}_i(A)$
or edges that are incident to a vertex that has at least
![]() ${5\Delta }/{9}$
incident edges in
${5\Delta }/{9}$
incident edges in
![]() ${\mathcal{B}}_i(A)$
. Let
${\mathcal{B}}_i(A)$
. Let
![]() ${\mathcal{B}}_\infty (A) = \bigcup _{i\in \mathbb{N}}{\mathcal{B}}_i(A)$
. It is shown in [Reference Helmuth, Jenssen and Perkins21, Lemma 12] that
${\mathcal{B}}_\infty (A) = \bigcup _{i\in \mathbb{N}}{\mathcal{B}}_i(A)$
. It is shown in [Reference Helmuth, Jenssen and Perkins21, Lemma 12] that
![]() $|{\mathcal{B}}_\infty (A)|\leq 10|{\mathcal{B}}_0(A)|$
.
$|{\mathcal{B}}_\infty (A)|\leq 10|{\mathcal{B}}_0(A)|$
.
An ordered polymer is a connected subgraph
![]() $\gamma =(V(\gamma ),E(\gamma ))$
of
$\gamma =(V(\gamma ),E(\gamma ))$
of
![]() $G$
together with an edge configuration
$G$
together with an edge configuration
![]() $\ell : E(\gamma )\rightarrow \{0,1\}$
subject to: (i)
$\ell : E(\gamma )\rightarrow \{0,1\}$
subject to: (i)
![]() $\mathrm{Out}(\ell )\leq \eta m$
, and (ii)
$\mathrm{Out}(\ell )\leq \eta m$
, and (ii)
![]() ${\mathcal{B}}_{\infty }(\mathrm{Out}(\ell ))=E(\gamma )$
. We let
${\mathcal{B}}_{\infty }(\mathrm{Out}(\ell ))=E(\gamma )$
. We let
![]() $E_{u}(\gamma )$
be the set of unoccupied edges
$E_{u}(\gamma )$
be the set of unoccupied edges
![]() $\mathrm{Out}(\ell )$
of the polymer and
$\mathrm{Out}(\ell )$
of the polymer and
![]() $c'(\gamma )$
be the number of components in the graph
$c'(\gamma )$
be the number of components in the graph
![]() $G[E\backslash E_{u}(\gamma )]$
with fewer than
$G[E\backslash E_{u}(\gamma )]$
with fewer than
![]() $n/2$
vertices. The size of
$n/2$
vertices. The size of
![]() $\gamma$
is defined as
$\gamma$
is defined as
![]() $|E_\gamma |$
, whereas the weight of
$|E_\gamma |$
, whereas the weight of
![]() $\gamma$
is defined as
$\gamma$
is defined as
![]() $w_\gamma ^{\mathrm{ord}} \;:\!=\; q^{c'(\gamma )} (e^\beta -1)^{-E_u(\gamma )}$
.
$w_\gamma ^{\mathrm{ord}} \;:\!=\; q^{c'(\gamma )} (e^\beta -1)^{-E_u(\gamma )}$
.
Given a (partial) configuration
![]() $\mathcal{F}$
, the set of ordered polymers of
$\mathcal{F}$
, the set of ordered polymers of
![]() $\mathcal{F}$
, denoted by
$\mathcal{F}$
, denoted by
![]() $\Gamma ({\mathcal{F}})$
, consists of the connected components of
$\Gamma ({\mathcal{F}})$
, consists of the connected components of
![]() $G[{\mathcal{B}}_\infty (\mathrm{Out}({\mathcal{F}}))]$
, each with the labelling on the edges induced by the corresponding assignment in
$G[{\mathcal{B}}_\infty (\mathrm{Out}({\mathcal{F}}))]$
, each with the labelling on the edges induced by the corresponding assignment in
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
We will use a couple of polymer properties from [Reference Helmuth, Jenssen and Perkins21]. First, we note the following connection between the weight of a configuration
![]() $\mathcal{F}$
to the weight of its polymers
$\mathcal{F}$
to the weight of its polymers
![]() $\Gamma ({\mathcal{F}})$
.
$\Gamma ({\mathcal{F}})$
.
Lemma 27.
Fix
![]() $\Delta \geq 5$
,
$\Delta \geq 5$
,
![]() $K\geq 0$
and
$K\geq 0$
and
![]() $\delta \in (0, 1/2)$
. Let
$\delta \in (0, 1/2)$
. Let
![]() $G\in{\mathcal{G}}_{\Delta, \delta, K}$
and
$G\in{\mathcal{G}}_{\Delta, \delta, K}$
and
![]() ${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
. Then
${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
. Then
![]() $w_G({\mathcal{F}}) = q(\mathrm{e}^\beta - 1)^{|E|} \prod _{\gamma \in \Gamma ({\mathcal{F}})} w_\gamma ^{\mathrm{ord}}$
.
$w_G({\mathcal{F}}) = q(\mathrm{e}^\beta - 1)^{|E|} \prod _{\gamma \in \Gamma ({\mathcal{F}})} w_\gamma ^{\mathrm{ord}}$
.
Proof. Note that
![]() $\mathrm{Out}({\mathcal{F}}) = \bigcup _{\gamma \in \Gamma ({\mathcal{F}})} E_u(\gamma )$
, so
$\mathrm{Out}({\mathcal{F}}) = \bigcup _{\gamma \in \Gamma ({\mathcal{F}})} E_u(\gamma )$
, so
![]() $(\mathrm{e}^\beta -1)^{|E| - \sum _{\gamma \in \Gamma ({\mathcal{F}})}|E_u(\gamma )|} = (\mathrm{e}^\beta -1)^{|{\mathrm{In}}({\mathcal{F}})|}.$
Hence, by [Reference Helmuth, Jenssen and Perkins21, Lemma21],
$(\mathrm{e}^\beta -1)^{|E| - \sum _{\gamma \in \Gamma ({\mathcal{F}})}|E_u(\gamma )|} = (\mathrm{e}^\beta -1)^{|{\mathrm{In}}({\mathcal{F}})|}.$
Hence, by [Reference Helmuth, Jenssen and Perkins21, Lemma21],
![]() $q^{\sum _{\gamma \in \Gamma ({\mathcal{F}})} c'(\gamma )} = q^{c(G[{\mathrm{In}}({\mathcal{F}})]) - 1}$
, so the result follows.
$q^{\sum _{\gamma \in \Gamma ({\mathcal{F}})} c'(\gamma )} = q^{c(G[{\mathrm{In}}({\mathcal{F}})]) - 1}$
, so the result follows.
Lemma 28.
Let
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K\geq 0$
be integers,
$K\geq 0$
be integers,
![]() $\delta \in (0, 1/2)$
be real. Then, for all sufficiently large
$\delta \in (0, 1/2)$
be real. Then, for all sufficiently large
![]() $q$
, the following holds for all
$q$
, the following holds for all
![]() $\beta \geq \log (q^{1.9/\Delta }+1)$
. For
$\beta \geq \log (q^{1.9/\Delta }+1)$
. For
![]() $G\in{\mathcal{G}}_{\Delta, \delta, K}$
with
$G\in{\mathcal{G}}_{\Delta, \delta, K}$
with
![]() $n=|V(G)|$
, for
$n=|V(G)|$
, for
![]() $s\;:\!=\;{2000}\log (n)/\beta$
,
$s\;:\!=\;{2000}\log (n)/\beta$
,
Proof. This proof closely follows the proof of Proposition 15 from [Reference Helmuth, Jenssen and Perkins21]. Suppose that
![]() $q$
is large enough so that
$q$
is large enough so that
![]() $q^{1.9/\Delta }\geq (2\mathrm{e}\Delta )^{400}$
and fix arbitrary
$q^{1.9/\Delta }\geq (2\mathrm{e}\Delta )^{400}$
and fix arbitrary
![]() $\beta \geq \log (q^{1.9/\Delta }+1)$
.
$\beta \geq \log (q^{1.9/\Delta }+1)$
.
Consider an arbitrary ordered polymer
![]() $\gamma$
. For any configuration
$\gamma$
. For any configuration
![]() ${\mathcal{F}}\in \Omega ^{{\mathrm{ord}}}$
with
${\mathcal{F}}\in \Omega ^{{\mathrm{ord}}}$
with
![]() $\gamma \in \Gamma ({\mathcal{F}})$
, by Lemma27, it holds that
$\gamma \in \Gamma ({\mathcal{F}})$
, by Lemma27, it holds that
![]() $w_G({\mathcal{F}}) \leq q(\mathrm{e}^\beta - 1)^{|E|} w_\gamma ^{\mathrm{ord}}$
. Note that for any
$w_G({\mathcal{F}}) \leq q(\mathrm{e}^\beta - 1)^{|E|} w_\gamma ^{\mathrm{ord}}$
. Note that for any
![]() ${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
such that
${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
such that
![]() $\gamma \in \Gamma ({\mathcal{F}})$
, there is a configuration
$\gamma \in \Gamma ({\mathcal{F}})$
, there is a configuration
![]() ${\mathcal{F}}'$
with
${\mathcal{F}}'$
with
![]() $\Gamma ({\mathcal{F}}') = \Gamma ({\mathcal{F}})\setminus \{\gamma \}$
(obtained by setting
$\Gamma ({\mathcal{F}}') = \Gamma ({\mathcal{F}})\setminus \{\gamma \}$
(obtained by setting
![]() ${\mathrm{In}}({\mathcal{F}}') ={\mathrm{In}}({\mathcal{F}})\cup E_u(\gamma )$
), which therefore has weight
${\mathrm{In}}({\mathcal{F}}') ={\mathrm{In}}({\mathcal{F}})\cup E_u(\gamma )$
), which therefore has weight
![]() $w_G({\mathcal{F}}') = w_G({\mathcal{F}})/w_\gamma ^{\mathrm{ord}}$
.
$w_G({\mathcal{F}}') = w_G({\mathcal{F}})/w_\gamma ^{\mathrm{ord}}$
.
Let
![]() $\Omega _\gamma$
be the set of all ordered configurations with a polymer
$\Omega _\gamma$
be the set of all ordered configurations with a polymer
![]() $\gamma$
. We can lower bound
$\gamma$
. We can lower bound
![]() $Z^{\mathrm{ord}}$
by
$Z^{\mathrm{ord}}$
by
![]() $\sum _{{\mathcal{F}}\in \Omega _\gamma } (w_G({\mathcal{F}}) + w_G({\mathcal{F}}')) = (1 + \frac{1}{w_\gamma ^{\mathrm{ord}}}) \sum _{{\mathcal{F}}\in \Omega _\gamma } w_G({\mathcal{F}})$
. Therefore,
$\sum _{{\mathcal{F}}\in \Omega _\gamma } (w_G({\mathcal{F}}) + w_G({\mathcal{F}}')) = (1 + \frac{1}{w_\gamma ^{\mathrm{ord}}}) \sum _{{\mathcal{F}}\in \Omega _\gamma } w_G({\mathcal{F}})$
. Therefore,
 \begin{equation*} \pi ^{\mathrm {ord}}(\gamma \in \Gamma (\cdot )) = \frac {\sum _{{\mathcal {F}}\in \Omega _\gamma } w_G({\mathcal {F}})}{Z^{\mathrm {ord}}} \leq \frac {1}{1 + \frac {1}{w_\gamma ^{\mathrm {ord}}}}\leq w_\gamma ^{\mathrm {ord}}, \end{equation*}
\begin{equation*} \pi ^{\mathrm {ord}}(\gamma \in \Gamma (\cdot )) = \frac {\sum _{{\mathcal {F}}\in \Omega _\gamma } w_G({\mathcal {F}})}{Z^{\mathrm {ord}}} \leq \frac {1}{1 + \frac {1}{w_\gamma ^{\mathrm {ord}}}}\leq w_\gamma ^{\mathrm {ord}}, \end{equation*}
so we conclude that the probability that any fixed polymer
![]() $\gamma$
is a polymer of
$\gamma$
is a polymer of
![]() ${\mathcal{F}}\sim \pi ^{\mathrm{ord}}_G$
is at most
${\mathcal{F}}\sim \pi ^{\mathrm{ord}}_G$
is at most
![]() $w_\gamma ^{\mathrm{ord}}$
.
$w_\gamma ^{\mathrm{ord}}$
.
Let
![]() $u$
be a vertex in
$u$
be a vertex in
![]() $V(G)$
and denote by
$V(G)$
and denote by
![]() $\Gamma _u$
the set of polymers containing
$\Gamma _u$
the set of polymers containing
![]() $u$
. Let
$u$
. Let
![]() $p_u$
be the probability that
$p_u$
be the probability that
![]() $u$
is contained in a polymer of size at least
$u$
is contained in a polymer of size at least
![]() $s$
for
$s$
for
![]() ${\mathcal{F}}\sim \pi ^{\mathrm{ord}}_G$
. By a union bound over the polymers in
${\mathcal{F}}\sim \pi ^{\mathrm{ord}}_G$
. By a union bound over the polymers in
![]() $\Gamma _u$
, We have that
$\Gamma _u$
, We have that
![]() $p_u\leq P_u$
, where
$p_u\leq P_u$
, where
By [Reference Helmuth, Jenssen and Perkins21, Lemma 14],
![]() $c'(\gamma )\leq 9|E_u(\gamma )|/(5 \Delta )$
. The bound on
$c'(\gamma )\leq 9|E_u(\gamma )|/(5 \Delta )$
. The bound on
![]() $\beta$
ensures that
$\beta$
ensures that
Hence we get
By [Reference Helmuth, Jenssen and Perkins21, Lemma 12], for any ordered polymer
![]() $\gamma$
,
$\gamma$
,
![]() $|E(\gamma )|\leq 10|E_u(\gamma )|$
. Thus
$|E(\gamma )|\leq 10|E_u(\gamma )|$
. Thus
By [Reference Helmuth, Jenssen and Perkins21, Proof of Proposition 15], the number of polymers with
![]() $k$
unoccupied edges containing a particular vertex is at most
$k$
unoccupied edges containing a particular vertex is at most
![]() $(2\mathrm{e}\Delta )^{10k}$
, hence
$(2\mathrm{e}\Delta )^{10k}$
, hence
By the lower bounds on
![]() $\beta$
and
$\beta$
and
![]() $q$
, we have
$q$
, we have
![]() $\mathrm{e}^{\beta }-1\geq q^{1.9/\Delta }\geq (2\mathrm{e}\Delta )^{400}$
so
$\mathrm{e}^{\beta }-1\geq q^{1.9/\Delta }\geq (2\mathrm{e}\Delta )^{400}$
so
The last sum is a geometric series with ratio
![]() $\mathrm{e}^{-\beta /80}\lt 1/2$
, so it is upper bounded by twice its largest term. Since
$\mathrm{e}^{-\beta /80}\lt 1/2$
, so it is upper bounded by twice its largest term. Since
![]() $s=\tfrac{2000}{\beta }\log n$
, it follows that
$s=\tfrac{2000}{\beta }\log n$
, it follows that
![]() $P_u\leq 2/n^{5/2}$
. By a union bound over the vertices of
$P_u\leq 2/n^{5/2}$
. By a union bound over the vertices of
![]() $G$
, the probability that there is a polymer of
$G$
, the probability that there is a polymer of
![]() ${\mathcal{F}}\sim \pi ^{{\mathrm{ord}}}_G$
which has size at least
${\mathcal{F}}\sim \pi ^{{\mathrm{ord}}}_G$
which has size at least
![]() $s$
is therefore at most
$s$
is therefore at most
![]() $2/n^{3/2}$
, as required.
$2/n^{3/2}$
, as required.
Furthermore, we can prove the following lemma based on the proof of [Reference Helmuth, Jenssen and Perkins21, Lemma21].
Lemma 29.
Fix
![]() $\Delta \geq 5$
,
$\Delta \geq 5$
,
![]() $K\geq 0$
and
$K\geq 0$
and
![]() $\delta \in (0,1/2)$
. Suppose
$\delta \in (0,1/2)$
. Suppose
![]() $n\geq 2/\delta$
. Let
$n\geq 2/\delta$
. Let
![]() $G=(V,E)$
with
$G=(V,E)$
with
![]() $|V|=n$
be a graph in
$|V|=n$
be a graph in
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
. Consider
${\mathcal{G}}_{\Delta, \delta, K}$
. Consider
![]() ${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
. Let
${\mathcal{F}}\in \Omega ^{\mathrm{ord}}$
. Let
![]() $\kappa$
be the giant component of
$\kappa$
be the giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}})]$
(which exists by Corollary 20
).
$G[{\mathrm{In}}({\mathcal{F}})]$
(which exists by Corollary 20
).
-
1. If
 $u\notin \kappa$
and
$u\notin \kappa$
and
 $e$
is incident to
$e$
is incident to
 $u$
then
$u$
then
 $e$
is in a polymer of
$e$
is in a polymer of
 $\mathcal{F}$
.
$\mathcal{F}$
. -
2. Let
 $S$
be a non-empty set of edges with
$S$
be a non-empty set of edges with
 $|S| \lt{9\Delta n}/{200}$
. Let
$|S| \lt{9\Delta n}/{200}$
. Let
 $\kappa '$
be a component of
$\kappa '$
be a component of
 $G[{\mathrm{In}}({\mathcal{F}})\backslash S]$
with
$G[{\mathrm{In}}({\mathcal{F}})\backslash S]$
with
 $|V(\kappa ')| \lt n/2$
. Then all but at most
$|V(\kappa ')| \lt n/2$
. Then all but at most
 $45\Delta |S|$
vertices of
$45\Delta |S|$
vertices of
 $\kappa '$
are such that all their incident edges belong to a polymer of
$\kappa '$
are such that all their incident edges belong to a polymer of
 $\mathcal{F}$
.
$\mathcal{F}$
. -
3. For
 $S$
and
$S$
and
 $\kappa '$
as in Item
2
, there are at most
$\kappa '$
as in Item
2
, there are at most
 $50\Delta ^2|S|$
components in
$50\Delta ^2|S|$
components in
 $G[{\mathcal{B}}_\infty (\mathrm{Out}({\mathcal{F}}))]$
containing a vertex of
$G[{\mathcal{B}}_\infty (\mathrm{Out}({\mathcal{F}}))]$
containing a vertex of
 $\kappa '$
, that is, there are at most
$\kappa '$
, that is, there are at most
 $50\Delta ^2|S|$
polymers of
$50\Delta ^2|S|$
polymers of
 $\mathcal{F}$
containing vertices of
$\mathcal{F}$
containing vertices of
 $\kappa '$
.
$\kappa '$
.
Proof. We start with the proof of Item 1. Consider a non-giant component
![]() $\kappa '$
of
$\kappa '$
of
![]() $G[{\mathrm{In}}({\mathcal{F}})]$
. Let
$G[{\mathrm{In}}({\mathcal{F}})]$
. Let
![]() $\tau$
be the set of vertices in
$\tau$
be the set of vertices in
![]() $\kappa '$
which have an incident edge that is not in a polymer of
$\kappa '$
which have an incident edge that is not in a polymer of
![]() $\mathcal{F}$
. For contradiction, assume that
$\mathcal{F}$
. For contradiction, assume that
![]() $\tau$
is non-empty. By Corollary20,
$\tau$
is non-empty. By Corollary20,
![]() $|\kappa '|\leq \delta |V|$
and thus
$|\kappa '|\leq \delta |V|$
and thus
![]() $|\tau |\leq \delta |V|$
. The definition of
$|\tau |\leq \delta |V|$
. The definition of
![]() $\tau$
and the fact that out-edges are in polymers imply that every edge in the cut
$\tau$
and the fact that out-edges are in polymers imply that every edge in the cut
![]() $(\tau, V\backslash \tau )$
is in some polymer. By the expansion properties
$(\tau, V\backslash \tau )$
is in some polymer. By the expansion properties
![]() $|E(\tau, V \backslash \tau )|\geq 5\Delta |\tau |/9$
, hence there is a vertex
$|E(\tau, V \backslash \tau )|\geq 5\Delta |\tau |/9$
, hence there is a vertex
![]() $u\in \tau$
with at least
$u\in \tau$
with at least
![]() ${5\Delta }/{9}$
incident edges in the cut, and thus, from the definition of polymers, all edges adjacent to
${5\Delta }/{9}$
incident edges in the cut, and thus, from the definition of polymers, all edges adjacent to
![]() $u$
are in polymers, contradicting that
$u$
are in polymers, contradicting that
![]() $u$
is in
$u$
is in
![]() $\tau$
.
$\tau$
.
Before proving Item 2, we use it to prove Item 3. Let
![]() $\kappa '$
be a non-giant component in
$\kappa '$
be a non-giant component in
![]() $G[{\mathrm{In}}({\mathcal{F}})\backslash S]$
. As before, let
$G[{\mathrm{In}}({\mathcal{F}})\backslash S]$
. As before, let
![]() $\tau$
be the set of vertices in
$\tau$
be the set of vertices in
![]() $\kappa '$
which have an incident edge that is not in a polymer of
$\kappa '$
which have an incident edge that is not in a polymer of
![]() $\mathcal{F}$
. By Item 2,
$\mathcal{F}$
. By Item 2,
![]() $|\tau | \leq 45\Delta |S|$
. Let
$|\tau | \leq 45\Delta |S|$
. Let
![]() $E_\tau$
be the set of edges that are incident to vertices in
$E_\tau$
be the set of edges that are incident to vertices in
![]() $\tau$
. Note that
$\tau$
. Note that
![]() $G[V(\kappa '),E(\kappa ')]$
is connected, and removing an edge from a graph can increase the number of components by at most one. Thus,
$G[V(\kappa '),E(\kappa ')]$
is connected, and removing an edge from a graph can increase the number of components by at most one. Thus,
![]() $(V(\kappa '),E(\kappa ')\setminus E_\tau )$
has at most
$(V(\kappa '),E(\kappa ')\setminus E_\tau )$
has at most
![]() $1+\Delta |\tau |$
components. Any edges in these components are in polymers of
$1+\Delta |\tau |$
components. Any edges in these components are in polymers of
![]() $\mathcal{F}$
. Thus there are at most
$\mathcal{F}$
. Thus there are at most
![]() $1 + \Delta |\tau | \leq 50\Delta ^2|S|$
components of
$1 + \Delta |\tau | \leq 50\Delta ^2|S|$
components of
![]() $G[{\mathcal{B}}_\infty (\mathrm{Out}({\mathcal{F}}))]$
that contain vertices in
$G[{\mathcal{B}}_\infty (\mathrm{Out}({\mathcal{F}}))]$
that contain vertices in
![]() $V(\kappa ')$
, proving Item 3.
$V(\kappa ')$
, proving Item 3.
To finish, we prove Item 2. First we bound the size of
![]() $\kappa '$
. Since
$\kappa '$
. Since
![]() ${\mathcal{F}} \in \Omega ^{\mathrm{ord}}$
,
${\mathcal{F}} \in \Omega ^{\mathrm{ord}}$
,
![]() $|{\mathrm{In}}({\mathcal{F}})\backslash S| \geq (1 - \eta ) |E| - |S|$
. Since
$|{\mathrm{In}}({\mathcal{F}})\backslash S| \geq (1 - \eta ) |E| - |S|$
. Since
![]() $\eta \leq 1/100$
,
$\eta \leq 1/100$
,
![]() $\eta + \frac{|S|}{|E|} \lt 1/10 \leq \phi _G(1/2)$
, hence we can apply Lemma17 with
$\eta + \frac{|S|}{|E|} \lt 1/10 \leq \phi _G(1/2)$
, hence we can apply Lemma17 with
![]() $E' = \mathrm{Out}({\mathcal{F}}) \cup S$
and
$E' = \mathrm{Out}({\mathcal{F}}) \cup S$
and
![]() $\theta = |E'|/|E|$
. We find that
$\theta = |E'|/|E|$
. We find that
![]() $(V,{\mathrm{In}}({\mathcal{F}}) \backslash S)$
has a component of size at least
$(V,{\mathrm{In}}({\mathcal{F}}) \backslash S)$
has a component of size at least
![]() $(1 - \frac{\theta }{2 \phi _G(1/2)}) n \geq (1 -{5 \theta } ) n$
so the number of vertices in
$(1 - \frac{\theta }{2 \phi _G(1/2)}) n \geq (1 -{5 \theta } ) n$
so the number of vertices in
![]() $\kappa '$
is at most
$\kappa '$
is at most
![]() $5 \theta n \leq 5(\eta + |S|/|E|)n \leq \delta n + 10|S|/\Delta$
. Thus,
$5 \theta n \leq 5(\eta + |S|/|E|)n \leq \delta n + 10|S|/\Delta$
. Thus,
![]() $|\tau | \leq \delta n + 10 |S|/\Delta$
. Next let
$|\tau | \leq \delta n + 10 |S|/\Delta$
. Next let
![]() $\lambda = \lceil 10 |S|/\Delta \rceil$
and let
$\lambda = \lceil 10 |S|/\Delta \rceil$
and let
![]() $U$
be a subset of
$U$
be a subset of
![]() $\tau$
of size
$\tau$
of size
![]() $|\tau | - \lambda \leq \delta n$
. Then
$|\tau | - \lambda \leq \delta n$
. Then
 \begin{align*} |E(\tau, V\backslash \tau )| &\geq |E(U,V\setminus \tau )| \\[5pt] &\geq |E(U,V\setminus U)| - |E(U,\tau \setminus U)|\\[5pt] &\geq \tfrac 59 \Delta |U| - \lambda \Delta = \tfrac 59 \Delta |\tau | - 14 \lambda \Delta /9. \end{align*}
\begin{align*} |E(\tau, V\backslash \tau )| &\geq |E(U,V\setminus \tau )| \\[5pt] &\geq |E(U,V\setminus U)| - |E(U,\tau \setminus U)|\\[5pt] &\geq \tfrac 59 \Delta |U| - \lambda \Delta = \tfrac 59 \Delta |\tau | - 14 \lambda \Delta /9. \end{align*}
By the definition of
![]() $\tau$
, all edges in
$\tau$
, all edges in
![]() $E(\tau, V(\kappa ')\setminus \tau )$
are in polymers of
$E(\tau, V(\kappa ')\setminus \tau )$
are in polymers of
![]() $\mathcal{F}$
. Since
$\mathcal{F}$
. Since
![]() $\kappa '$
is a component of
$\kappa '$
is a component of
![]() $G[{\mathrm{In}}({\mathcal{F}})\setminus S]$
, there are at most
$G[{\mathrm{In}}({\mathcal{F}})\setminus S]$
, there are at most
![]() $|S|$
edges in
$|S|$
edges in
![]() ${\mathrm{In}}({\mathcal{F}})$
between
${\mathrm{In}}({\mathcal{F}})$
between
![]() $\tau$
and
$\tau$
and
![]() $V\setminus V(\kappa ')$
. Thus the number of edges in
$V\setminus V(\kappa ')$
. Thus the number of edges in
![]() $E(\tau, V\setminus \tau )$
that are in polymers is at least
$E(\tau, V\setminus \tau )$
that are in polymers is at least
![]() $|E(\tau, V\backslash \tau )| - |S|$
. This is at least
$|E(\tau, V\backslash \tau )| - |S|$
. This is at least
![]() $\tfrac 59 \Delta |\tau | - 14 \lambda \Delta /9 - |S| \geq \tfrac 59 \Delta |\tau | - 149 |S|/9 - 14\Delta /9 \geq \tfrac 59 \Delta |\tau | - 45 \Delta |S|/9$
, where the last inequality follows from
$\tfrac 59 \Delta |\tau | - 14 \lambda \Delta /9 - |S| \geq \tfrac 59 \Delta |\tau | - 149 |S|/9 - 14\Delta /9 \geq \tfrac 59 \Delta |\tau | - 45 \Delta |S|/9$
, where the last inequality follows from
![]() $\Delta \geq 5$
,
$\Delta \geq 5$
,
![]() $|S|\geq 1$
.
$|S|\geq 1$
.
Averaged over all vertices
![]() $w\in \tau$
, the number of edges in
$w\in \tau$
, the number of edges in
![]() $E(\tau, V\setminus \tau )$
that are in polymers and are incident to
$E(\tau, V\setminus \tau )$
that are in polymers and are incident to
![]() $w$
is at least
$w$
is at least
![]() $\tfrac 59 \Delta - 45 \Delta |S|/(9\tau )$
. We may assume
$\tfrac 59 \Delta - 45 \Delta |S|/(9\tau )$
. We may assume
![]() $\tau$
is non-empty, otherwise Item 2 directly follows. Thus, there is a vertex
$\tau$
is non-empty, otherwise Item 2 directly follows. Thus, there is a vertex
![]() $w\in \tau$
such that the number of edges in
$w\in \tau$
such that the number of edges in
![]() $E(\tau, V\setminus \tau )$
that are in polymers and are incident to
$E(\tau, V\setminus \tau )$
that are in polymers and are incident to
![]() $w$
is at least
$w$
is at least
![]() $\tfrac 59 \Delta - 45 \Delta |S|/(9\tau )$
. Since this number is an integer, the number of edges in
$\tfrac 59 \Delta - 45 \Delta |S|/(9\tau )$
. Since this number is an integer, the number of edges in
![]() $E(\tau, V\setminus \tau )$
that are in polymers and are incident to
$E(\tau, V\setminus \tau )$
that are in polymers and are incident to
![]() $w$
is at least
$w$
is at least
Suppose for contradiction that
![]() $|\tau | \gt 45\Delta |S|$
. Then the term that is subtracted in the definition of
$|\tau | \gt 45\Delta |S|$
. Then the term that is subtracted in the definition of
![]() $W$
is less than
$W$
is less than
![]() $1/9$
. On the other hand, if the first term,
$1/9$
. On the other hand, if the first term,
![]() $5\Delta /9$
is not an integer, then its non-integer part is at least
$5\Delta /9$
is not an integer, then its non-integer part is at least
![]() $1/9$
. Either way,
$1/9$
. Either way,
![]() $W = \lceil 5 \Delta /9\rceil \geq 5\Delta /9$
. As in the proof of Item 1, all incident edges of
$W = \lceil 5 \Delta /9\rceil \geq 5\Delta /9$
. As in the proof of Item 1, all incident edges of
![]() $w$
hence must be a in a polymer, contradicting that
$w$
hence must be a in a polymer, contradicting that
![]() $w\in \tau$
.
$w\in \tau$
.
5. Proving WSM within the ordered phase
In this section we will prove Theorem5. We will use the following notation.
Definition 30.
Let
![]() $G=(V,E)$
be a graph. Given vertices
$G=(V,E)$
be a graph. Given vertices
![]() $u,v\in V$
, let
$u,v\in V$
, let
![]() $d_G(v,u)$
be the distance in
$d_G(v,u)$
be the distance in
![]() $G$
from
$G$
from
![]() $v$
to
$v$
to
![]() $u$
. For
$u$
. For
![]() $U\subseteq V$
and
$U\subseteq V$
and
![]() $F\subseteq E$
, denote by
$F\subseteq E$
, denote by
![]() $d_G(v,U)$
the min distance in
$d_G(v,U)$
the min distance in
![]() $G$
from
$G$
from
![]() $v$
to any vertex in
$v$
to any vertex in
![]() $U$
, and by
$U$
, and by
![]() $d_G(v,F)$
the min distance in
$d_G(v,F)$
the min distance in
![]() $G$
to any endpoint of any edge in
$G$
to any endpoint of any edge in
![]() $F$
. Let
$F$
. Let
![]() $\partial _G(F)$
be the set of vertices in
$\partial _G(F)$
be the set of vertices in
![]() $V$
incident to both an edge in
$V$
incident to both an edge in
![]() $F$
and an edge in
$F$
and an edge in
![]() $E\backslash F$
. For a rooted tree
$E\backslash F$
. For a rooted tree
![]() $T$
and a vertex
$T$
and a vertex
![]() $u\in V(T)$
, let
$u\in V(T)$
, let
![]() $T_u$
denote the subtree of
$T_u$
denote the subtree of
![]() $T$
rooted at
$T$
rooted at
![]() $u$
.
$u$
.
Fix positive integers
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K\geq 0$
. Let
$K\geq 0$
. Let
![]() $M = M(K,\Delta )=2000 \times 400 \times (2+K) \Delta \log (\Delta -1)$
. Fix
$M = M(K,\Delta )=2000 \times 400 \times (2+K) \Delta \log (\Delta -1)$
. Fix
![]() $q$
sufficiently large and
$q$
sufficiently large and
![]() $\beta \geq \beta _c$
. Fix a graph
$\beta \geq \beta _c$
. Fix a graph
![]() $G=(V,E)\in{\mathcal{G}}_{\Delta, \delta, K}$
with
$G=(V,E)\in{\mathcal{G}}_{\Delta, \delta, K}$
with
![]() $n=|V|$
sufficiently large and fix a vertex
$n=|V|$
sufficiently large and fix a vertex
![]() $v\in V$
. Let
$v\in V$
. Let
![]() $r \;:\!=\; \min (\tfrac{M}\beta, \tfrac 13) \log _{\Delta -1} n$
.
$r \;:\!=\; \min (\tfrac{M}\beta, \tfrac 13) \log _{\Delta -1} n$
.
Definition 31.
Consider a breadth-first search from
![]() $v$
in
$v$
in
![]() $G[B_r(v)]$
. Let
$G[B_r(v)]$
. Let
![]() $T_0$
be the rooted tree consisting of all forward edges in this breadth-first search. We refer to edges in
$T_0$
be the rooted tree consisting of all forward edges in this breadth-first search. We refer to edges in
![]() $E(T_0)$
as the tree edges. We refer to the edges in
$E(T_0)$
as the tree edges. We refer to the edges in
![]() $\mathcal{E} \;:\!=\; E(B_r(v)) \backslash E(T_0)$
as excess edges.
$\mathcal{E} \;:\!=\; E(B_r(v)) \backslash E(T_0)$
as excess edges.
Observation 32.
For every edge
![]() $\{u,u'\}$
in
$\{u,u'\}$
in
![]() $\mathcal{E}$
,
$\mathcal{E}$
,
![]() $d_{T_0}(v,u)$
and
$d_{T_0}(v,u)$
and
![]() $d_{T_0}(v,u')$
differ by at most one. For any
$d_{T_0}(v,u')$
differ by at most one. For any
![]() $u\in B_r(v)$
,
$u\in B_r(v)$
,
![]() $d_G(v,u) = d_{T_0}(v,u)$
.
$d_G(v,u) = d_{T_0}(v,u)$
.
Since
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
,
${\mathcal{G}}_{\Delta, \delta, K}$
,
![]() $|\mathcal{E}|\leq K$
so the ball
$|\mathcal{E}|\leq K$
so the ball
![]() $B_r(v)$
is close to being a tree. The next observation picks out a piece of
$B_r(v)$
is close to being a tree. The next observation picks out a piece of
![]() $B_r(v)$
without excess edges.
$B_r(v)$
without excess edges.
Observation 33.
Suppose
![]() $r \gt K+1$
. Then there are integers
$r \gt K+1$
. Then there are integers
![]() $r_1$
and
$r_1$
and
![]() $r_2$
satisfying
$r_2$
satisfying
![]() $r \geq r_1 \gt r_2 \geq 0$
such that
$r \geq r_1 \gt r_2 \geq 0$
such that
![]() $E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
contains no edges from
$E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
contains no edges from
![]() $\mathcal{E}$
and
$\mathcal{E}$
and
![]() $r_1 - r_2 \geq \frac{r}{1 + K} - 1$
.
$r_1 - r_2 \geq \frac{r}{1 + K} - 1$
.
Proof. For every edge
![]() $e$
of
$e$
of
![]() $G$
, let
$G$
, let
![]() $d^+(v,e)$
denote the maximum distance in
$d^+(v,e)$
denote the maximum distance in
![]() $G$
from
$G$
from
![]() $v$
to an endpoint of
$v$
to an endpoint of
![]() $e$
. Let
$e$
. Let
![]() $\mathcal{D} = \{ d^+_G(e) \mid e \in \mathcal{E}\}$
. Note that
$\mathcal{D} = \{ d^+_G(e) \mid e \in \mathcal{E}\}$
. Note that
![]() $|\mathcal{D}| \leq K$
. Thus the set
$|\mathcal{D}| \leq K$
. Thus the set
![]() $\{1,2,\ldots, \lfloor r\rfloor \} \backslash \mathcal{D}$
can be partitioned into at most
$\{1,2,\ldots, \lfloor r\rfloor \} \backslash \mathcal{D}$
can be partitioned into at most
![]() $K + 1$
intervals of contiguous distances. Thus, there are integers
$K + 1$
intervals of contiguous distances. Thus, there are integers
![]() $r_1$
and
$r_1$
and
![]() $r'_2$
with
$r'_2$
with
![]() $r_1 \geq r_2'$
such that the set
$r_1 \geq r_2'$
such that the set
![]() $\{r_2', r_2' + 1, \dots, r_1\}$
does not intersect
$\{r_2', r_2' + 1, \dots, r_1\}$
does not intersect
![]() $\mathcal{D}$
and
$\mathcal{D}$
and
![]() $r_1 - r_2' + 1 \geq \frac{\lfloor r\rfloor - K}{K + 1} \geq \frac{r - 1 - K}{K + 1} = \frac{r}{K+1} - 1$
.
$r_1 - r_2' + 1 \geq \frac{\lfloor r\rfloor - K}{K + 1} \geq \frac{r - 1 - K}{K + 1} = \frac{r}{K+1} - 1$
.
Let
![]() $r_2 = r_2' - 1$
. We claim that
$r_2 = r_2' - 1$
. We claim that
![]() $(E(B_{r_1}(v))\backslash E(B_{r_2}(v)))\cap \mathcal{E} = \emptyset$
. To see this, consider any
$(E(B_{r_1}(v))\backslash E(B_{r_2}(v)))\cap \mathcal{E} = \emptyset$
. To see this, consider any
![]() $ e \in \mathcal{E}$
. By the choice of
$ e \in \mathcal{E}$
. By the choice of
![]() $r_1$
and
$r_1$
and
![]() $ r_2$
, either
$ r_2$
, either
![]() $d^+(v,e)\gt r_1$
or
$d^+(v,e)\gt r_1$
or
![]() $ d^+(v,e)\leq r_2$
. In the former case, an endpoint of
$ d^+(v,e)\leq r_2$
. In the former case, an endpoint of
![]() $e$
is outside
$e$
is outside
![]() $V(B_{r_1}(v))$
, thus
$V(B_{r_1}(v))$
, thus
![]() $e \notin B_{r_1}(v)$
. In the latter case, both endpoints of
$e \notin B_{r_1}(v)$
. In the latter case, both endpoints of
![]() $e$
are in
$e$
are in
![]() $B_{r_2}(v)$
, thus
$B_{r_2}(v)$
, thus
![]() $ e\in B_{r_2}(v)$
. That concludes the proof.
$ e\in B_{r_2}(v)$
. That concludes the proof.
5.1 Definitions/Notation
In addition to a configurations, we will work with partial configurations, where some edges are not yet revealed. We will use the symbol ‘
![]() $*$
’ to denote that an edge
$*$
’ to denote that an edge
![]() $e$
has not yet been revealed.
$e$
has not yet been revealed.
Definition 34.
A partial configuration
![]() $\mathcal{A}$
is a function
$\mathcal{A}$
is a function
![]() ${\mathcal{A}} : E \rightarrow \{0,1,*\}$
. We write
${\mathcal{A}} : E \rightarrow \{0,1,*\}$
. We write
![]() $R({\mathcal{A}}) \;:\!=\;{\mathcal{A}}^{-1}(\{0,1\})$
and refer to it as the set of revealed edges in
$R({\mathcal{A}}) \;:\!=\;{\mathcal{A}}^{-1}(\{0,1\})$
and refer to it as the set of revealed edges in
![]() $\mathcal{A}$
. We denote by
$\mathcal{A}$
. We denote by
![]() ${\mathrm{In}}({\mathcal{A}})$
the set of edges
${\mathrm{In}}({\mathcal{A}})$
the set of edges
![]() $e$
with
$e$
with
![]() ${\mathcal{A}}(e)=1$
(the ‘in’ edges) and by
${\mathcal{A}}(e)=1$
(the ‘in’ edges) and by
![]() $\mathrm{Out}({\mathcal{A}})$
the set of edges
$\mathrm{Out}({\mathcal{A}})$
the set of edges
![]() $e$
with
$e$
with
![]() ${\mathcal{A}}(e)=0$
(the ‘out’ edges). We use
${\mathcal{A}}(e)=0$
(the ‘out’ edges). We use
![]() $\Omega ^*$
to denote the set of all partial configurations.
$\Omega ^*$
to denote the set of all partial configurations.
Note that each configuration is also a partial configuration – these are precisely the partial configurations
![]() $\mathcal{A}$
with
$\mathcal{A}$
with
![]() $R({\mathcal{A}})=E$
. Next we define notation for partial configurations.
$R({\mathcal{A}})=E$
. Next we define notation for partial configurations.
Definition 35.
Let
![]() ${\mathcal{A}}_1,{\mathcal{A}}_2$
be partial configurations. We say that
${\mathcal{A}}_1,{\mathcal{A}}_2$
be partial configurations. We say that
![]() ${\mathcal{A}}_2$
is a refinement of
${\mathcal{A}}_2$
is a refinement of
![]() ${\mathcal{A}}_1$
, written
${\mathcal{A}}_1$
, written
![]() ${\mathcal{A}}_1\subseteq{\mathcal{A}}_2$
, whenever
${\mathcal{A}}_1\subseteq{\mathcal{A}}_2$
, whenever
![]() ${\mathrm{In}}({\mathcal{A}}_1)\subseteq{\mathrm{In}}({\mathcal{A}}_2)$
and
${\mathrm{In}}({\mathcal{A}}_1)\subseteq{\mathrm{In}}({\mathcal{A}}_2)$
and
![]() $\mathrm{Out}({\mathcal{A}}_1)\subseteq \mathrm{Out}({\mathcal{A}}_2)$
(and hence
$\mathrm{Out}({\mathcal{A}}_1)\subseteq \mathrm{Out}({\mathcal{A}}_2)$
(and hence
![]() $R({\mathcal{A}}_1)\subseteq R({\mathcal{A}}_2)$
as well). If
$R({\mathcal{A}}_1)\subseteq R({\mathcal{A}}_2)$
as well). If
![]() $R({\mathcal{A}}_1)$
and
$R({\mathcal{A}}_1)$
and
![]() $R({\mathcal{A}}_2)$
are disjoint, the union of
$R({\mathcal{A}}_2)$
are disjoint, the union of
![]() ${\mathcal{A}}_1$
and
${\mathcal{A}}_1$
and
![]() ${\mathcal{A}}_2$
, written
${\mathcal{A}}_2$
, written
![]() ${\mathcal{A}}_1\cup{\mathcal{A}}_2$
, is the partial configuration with
${\mathcal{A}}_1\cup{\mathcal{A}}_2$
, is the partial configuration with
![]() ${\mathrm{In}}({\mathcal{A}}_1\cup{\mathcal{A}}_2) ={\mathrm{In}}({\mathcal{A}}_1)\cup{\mathrm{In}}({\mathcal{A}}_2)$
and
${\mathrm{In}}({\mathcal{A}}_1\cup{\mathcal{A}}_2) ={\mathrm{In}}({\mathcal{A}}_1)\cup{\mathrm{In}}({\mathcal{A}}_2)$
and
![]() $\mathrm{Out}({\mathcal{A}}_1\cup{\mathcal{A}}_2)=\mathrm{Out}({\mathcal{A}}_1)\cup \mathrm{Out}({\mathcal{A}}_2)$
.
$\mathrm{Out}({\mathcal{A}}_1\cup{\mathcal{A}}_2)=\mathrm{Out}({\mathcal{A}}_1)\cup \mathrm{Out}({\mathcal{A}}_2)$
.
The following distributions on configurations and partial configurations will be useful.
Definition 36.
Let
![]() $\mathcal{A}$
be a partial configuration in
$\mathcal{A}$
be a partial configuration in
![]() $\Omega ^*$
. Then
$\Omega ^*$
. Then
![]() $\Omega _{\mathcal{A}} \;:\!=\; \{{\mathcal{F}} \in \Omega \mid{\mathcal{A}} \subseteq{\mathcal{F}}\}$
will denote the set of all configurations that refine
$\Omega _{\mathcal{A}} \;:\!=\; \{{\mathcal{F}} \in \Omega \mid{\mathcal{A}} \subseteq{\mathcal{F}}\}$
will denote the set of all configurations that refine
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\pi _{\mathcal{A}}$
is the conditional distribution of
$\pi _{\mathcal{A}}$
is the conditional distribution of
![]() $\pi$
in
$\pi$
in
![]() $\Omega _{\mathcal{A}}$
, that is, for
$\Omega _{\mathcal{A}}$
, that is, for
![]() ${\mathcal{F}} \in \Omega _{\mathcal{A}}$
,
${\mathcal{F}} \in \Omega _{\mathcal{A}}$
,
![]() $\pi _{\mathcal{A}}({\mathcal{F}}) = \pi ({\mathcal{F}}) /\sum _{{\mathcal{F}}' \in \Omega _{\mathcal{A}}} \pi ({\mathcal{F}}')$
. Similarly, if
$\pi _{\mathcal{A}}({\mathcal{F}}) = \pi ({\mathcal{F}}) /\sum _{{\mathcal{F}}' \in \Omega _{\mathcal{A}}} \pi ({\mathcal{F}}')$
. Similarly, if
![]() $\Omega _{\mathcal{A}} \cap \Omega ^{\mathrm{ord}}$
is non-empty, then
$\Omega _{\mathcal{A}} \cap \Omega ^{\mathrm{ord}}$
is non-empty, then
![]() $\pi ^{\mathrm{ord}}_{\mathcal{A}}$
is the conditional distribution of
$\pi ^{\mathrm{ord}}_{\mathcal{A}}$
is the conditional distribution of
![]() $\pi ^{\mathrm{ord}}$
in
$\pi ^{\mathrm{ord}}$
in
![]() $\Omega _{\mathcal{A}}\cap \Omega ^{\mathrm{ord}}$
.
$\Omega _{\mathcal{A}}\cap \Omega ^{\mathrm{ord}}$
.
5.2 The coupling process
From now on, we assume that
![]() $n=|V(G)|$
is sufficiently large, so
$n=|V(G)|$
is sufficiently large, so
![]() $r\gt K + 1$
. We define
$r\gt K + 1$
. We define
![]() $r_1$
and
$r_1$
and
![]() $r_2$
as in Observation33. Note
$r_2$
as in Observation33. Note
![]() $r_1\geq \frac{r}{K+1}-1$
. Let
$r_1\geq \frac{r}{K+1}-1$
. Let
![]() $T = T_0[B_{r_1}(v)]$
be the first
$T = T_0[B_{r_1}(v)]$
be the first
![]() $r_1 + 1$
levels of the tree
$r_1 + 1$
levels of the tree
![]() $T_0$
. To prove Theorem5, we construct a coupling of
$T_0$
. To prove Theorem5, we construct a coupling of
![]() ${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}^+_{r_1}(v)}$
and
${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}^+_{r_1}(v)}$
and
![]() ${\mathcal{F}}^{\mathrm{ord}}\sim \pi ^{\mathrm{ord}}$
, such that
${\mathcal{F}}^{\mathrm{ord}}\sim \pi ^{\mathrm{ord}}$
, such that
![]() ${\mathbb{P}}({\mathcal{F}}^+(e)\neq{\mathcal{F}}^{\mathrm{ord}}(e)) \leq 1/(100 |E|)$
.
${\mathbb{P}}({\mathcal{F}}^+(e)\neq{\mathcal{F}}^{\mathrm{ord}}(e)) \leq 1/(100 |E|)$
.
To do this, we generate two sequences of coupled partial configurations, starting by revealing all edges outside the ball
![]() $B_{r_1}(v)$
and progressively revealing the edges of
$B_{r_1}(v)$
and progressively revealing the edges of
![]() $T$
, starting from its leaves. We reveal edges one subtree at a time until either the boundary is contained in a giant component of in edges, or an edge incident to
$T$
, starting from its leaves. We reveal edges one subtree at a time until either the boundary is contained in a giant component of in edges, or an edge incident to
![]() $B_{r_2}(v)$
is revealed. In the first case, we use Observation51 from Appendix B to couple edges incident to
$B_{r_2}(v)$
is revealed. In the first case, we use Observation51 from Appendix B to couple edges incident to
![]() $v$
perfectly. In the other case, we will be able to show the existence of a large polymer (which is an unlikely event).
$v$
perfectly. In the other case, we will be able to show the existence of a large polymer (which is an unlikely event).
Formally, we will construct a sequence of edge subsets
![]() $F_0 \subseteq F_1 \subseteq \cdots \subseteq E$
, sequence of vertex subsets
$F_0 \subseteq F_1 \subseteq \cdots \subseteq E$
, sequence of vertex subsets
![]() $V_0, V_1, \dots$
, and two sequences of partial configurations
$V_0, V_1, \dots$
, and two sequences of partial configurations
![]() ${\mathcal{F}}_0^+\subseteq{\mathcal{F}}_1^+\subseteq \dots \subseteq{\mathcal{F}}^+$
and
${\mathcal{F}}_0^+\subseteq{\mathcal{F}}_1^+\subseteq \dots \subseteq{\mathcal{F}}^+$
and
![]() ${\mathcal{F}}_0^{\mathrm{ord}}\subseteq{\mathcal{F}}_1^{\mathrm{ord}}\subseteq \dots \subseteq{\mathcal{F}}^{\mathrm{ord}}$
, maintaining the following invariant for all integers
${\mathcal{F}}_0^{\mathrm{ord}}\subseteq{\mathcal{F}}_1^{\mathrm{ord}}\subseteq \dots \subseteq{\mathcal{F}}^{\mathrm{ord}}$
, maintaining the following invariant for all integers
![]() $i\geq 0$
:
$i\geq 0$
:
For each
![]() $i$
, all unrevealed edges of some subtree of
$i$
, all unrevealed edges of some subtree of
![]() $T$
get revealed. It will also hold, for each
$T$
get revealed. It will also hold, for each
![]() $i$
, that
$i$
, that
![]() $E\setminus E(B_{r_1}(v)) \subseteq F_i$
. To facilitate this process of revealing the edges, the following definitions will be helpful.
$E\setminus E(B_{r_1}(v)) \subseteq F_i$
. To facilitate this process of revealing the edges, the following definitions will be helpful.
Definition 37.
Let
![]() $F$
be a subset of
$F$
be a subset of
![]() $E$
. Then
$E$
. Then
![]() $\Omega _{F} \;:\!=\; \{{\mathcal{A}} \in \Omega ^* \mid R({\mathcal{A}}) = F\}$
. The distribution
$\Omega _{F} \;:\!=\; \{{\mathcal{A}} \in \Omega ^* \mid R({\mathcal{A}}) = F\}$
. The distribution
![]() $\pi _F$
on
$\pi _F$
on
![]() $\Omega _F$
is defined as follows. For
$\Omega _F$
is defined as follows. For
![]() ${\mathcal{A}}\in \Omega _F$
,
${\mathcal{A}}\in \Omega _F$
,
![]() $\pi _F({\mathcal{A}}) \;:\!=\; \pi (\Omega _{\mathcal{A}})$
. Similarly,
$\pi _F({\mathcal{A}}) \;:\!=\; \pi (\Omega _{\mathcal{A}})$
. Similarly,
![]() $\pi ^{\mathrm{ord}}_F$
is the distribution on
$\pi ^{\mathrm{ord}}_F$
is the distribution on
![]() $\Omega _F$
so that
$\Omega _F$
so that
![]() $\pi _F^{\mathrm{ord}}({\mathcal{A}}) = \pi ^{\mathrm{ord}}(\Omega _{\mathcal{A}})$
.
$\pi _F^{\mathrm{ord}}({\mathcal{A}}) = \pi ^{\mathrm{ord}}(\Omega _{\mathcal{A}})$
.
Definition 38.
Let
![]() ${\mathcal{A}}\in \Omega ^*$
be a partial configuration. Let
${\mathcal{A}}\in \Omega ^*$
be a partial configuration. Let
![]() $F$
be a subset of
$F$
be a subset of
![]() $E$
with
$E$
with
![]() $R({\mathcal{A}}) \subseteq F$
. Then
$R({\mathcal{A}}) \subseteq F$
. Then
![]() $\Omega _{{\mathcal{A}},F} \;:\!=\; \{{\mathcal{A}}'\in \Omega _F \mid{\mathcal{A}}\subseteq{\mathcal{A}}', R({\mathcal{A}})=F\}$
. We define a distribution
$\Omega _{{\mathcal{A}},F} \;:\!=\; \{{\mathcal{A}}'\in \Omega _F \mid{\mathcal{A}}\subseteq{\mathcal{A}}', R({\mathcal{A}})=F\}$
. We define a distribution
![]() $\pi _{{\mathcal{A}},F}$
on
$\pi _{{\mathcal{A}},F}$
on
![]() $\Omega _{{\mathcal{A}},F}$
given by
$\Omega _{{\mathcal{A}},F}$
given by
We can now describe the process in detail.
-
Step 1. Let
 $i \;:\!=\; 0$
. Let
$i \;:\!=\; 0$
. Let
 $F_0 \;:\!=\; E \setminus E(B_{r_1}(v))$
. Let
$F_0 \;:\!=\; E \setminus E(B_{r_1}(v))$
. Let
 ${\mathcal{F}}_0^{\mathrm{ord}}\sim \pi ^{\mathrm{ord}}_{F_0}$
. Let
${\mathcal{F}}_0^{\mathrm{ord}}\sim \pi ^{\mathrm{ord}}_{F_0}$
. Let
 $V_0 \;:\!=\; \{ w\in V \mid d_G(v,w) = r_1\}$
.
$V_0 \;:\!=\; \{ w\in V \mid d_G(v,w) = r_1\}$
.-
(a) If
 $|{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{ord}})| \lt (1-\eta ) |E|$
: Generate
$|{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{ord}})| \lt (1-\eta ) |E|$
: Generate
 ${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}_{{\mathcal{F}}_0^{\mathrm{ord}}}$
and generate
${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}_{{\mathcal{F}}_0^{\mathrm{ord}}}$
and generate
 ${\mathcal{F}}^+_0\sim \pi _{{\mathcal{B}}_{r+1}^+(v)}$
. Let
${\mathcal{F}}^+_0\sim \pi _{{\mathcal{B}}_{r+1}^+(v)}$
. Let
 ${\mathcal{F}}^+ \;:\!=\;{\mathcal{F}}^+_0$
. Terminate (unsuccessfully).
${\mathcal{F}}^+ \;:\!=\;{\mathcal{F}}^+_0$
. Terminate (unsuccessfully). -
(b) Otherwise: Define
 ${\mathcal{F}}_0^+$
by
${\mathcal{F}}_0^+$
by
 $R({\mathcal{F}}_0^+) ={\mathrm{In}}({\mathcal{F}}_0^+) = F_0$
.
$R({\mathcal{F}}_0^+) ={\mathrm{In}}({\mathcal{F}}_0^+) = F_0$
.
-
-
Step 2. Repeat until
 $d_G(F_i, v) \leq r_2$
:
$d_G(F_i, v) \leq r_2$
:-
Let
 $W_i$
be the set of all vertices in
$W_i$
be the set of all vertices in
 $\partial _G(F_i)$
that are in a component of size less than
$\partial _G(F_i)$
that are in a component of size less than
 $n/2$
in
$n/2$
in
 $G[{\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})]$
.-
(a) If
 $W_i$
is non-empty: Choose
$W_i$
is non-empty: Choose
 $w_i \in W_i$
to maximise
$w_i \in W_i$
to maximise
 $d_G(w_i,v)$
. Let
$d_G(w_i,v)$
. Let
 $p_{i}$
be the parent of
$p_{i}$
be the parent of
 $w_i$
in
$w_i$
in
 $T$
. Let
$T$
. Let
 $F_{i+1} \;:\!=\; F_i \cup E(T_{p_i})$
. Generate, optimally coupled,
$F_{i+1} \;:\!=\; F_i \cup E(T_{p_i})$
. Generate, optimally coupled,
 ${\mathcal{F}}^{\mathrm{ord}}_{i+1}\sim \pi _{{\mathcal{F}}^{\mathrm{ord}}_i,F_{i+1}}$
and
${\mathcal{F}}^{\mathrm{ord}}_{i+1}\sim \pi _{{\mathcal{F}}^{\mathrm{ord}}_i,F_{i+1}}$
and
 ${\mathcal{F}}_{i+1}^+ \sim \pi _{{\mathcal{F}}^+_i,F_{i+1}}$
. Let
${\mathcal{F}}_{i+1}^+ \sim \pi _{{\mathcal{F}}^+_i,F_{i+1}}$
. Let
 $V_{i+1} \;:\!=\; (V_{i}\backslash V(T_{p_i}))\cup \{p_i\}$
. Let
$V_{i+1} \;:\!=\; (V_{i}\backslash V(T_{p_i}))\cup \{p_i\}$
. Let
 $i \;:\!=\; i + 1$
.
$i \;:\!=\; i + 1$
. -
(b) Otherwise: Generate, optimally coupled,
 ${\mathcal{F}}^{\mathrm{ord}}\sim \pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
and
${\mathcal{F}}^{\mathrm{ord}}\sim \pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
and
 ${\mathcal{F}}^+\sim \pi _{{\mathcal{F}}^+_i}$
and terminate (succesfully).
${\mathcal{F}}^+\sim \pi _{{\mathcal{F}}^+_i}$
and terminate (succesfully).
-
-
-
Step 3. Generate, optimally coupled,
 ${\mathcal{F}}^{\mathrm{ord}}\sim \pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
and
${\mathcal{F}}^{\mathrm{ord}}\sim \pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
and
 ${\mathcal{F}}^+\sim \pi _{{\mathcal{F}}^+_i}$
. Terminate (unsuccesfully).
${\mathcal{F}}^+\sim \pi _{{\mathcal{F}}^+_i}$
. Terminate (unsuccesfully).
We next derive some useful observations justifying the definition of the process. We will require the following definition.
Definition 39.
Let
![]() $\mathcal{A}$
be a partial configuration. The boundary component set
$\mathcal{A}$
be a partial configuration. The boundary component set
![]() $\xi ({\mathcal{A}})$
of
$\xi ({\mathcal{A}})$
of
![]() $\mathcal{A}$
is the set of equivalence classes corresponding to components of the boundary vertices, that is,
$\mathcal{A}$
is the set of equivalence classes corresponding to components of the boundary vertices, that is,
![]() $ \xi ({\mathcal{A}}) = \{ \kappa \cap \partial (R({\mathcal{A}})) \mid \kappa \text{ is a component in } G[{\mathrm{In}}({\mathcal{A}})]\}$
.
$ \xi ({\mathcal{A}}) = \{ \kappa \cap \partial (R({\mathcal{A}})) \mid \kappa \text{ is a component in } G[{\mathrm{In}}({\mathcal{A}})]\}$
.
Observation 40.
Suppose that the process does not terminate in Step 1a (with
![]() $i=0$
). Then it maintains the following invariants for all
$i=0$
). Then it maintains the following invariants for all
![]() $i\geq 0$
such that
$i\geq 0$
such that
![]() ${\mathcal{F}}_i^{\mathrm{ord}},{\mathcal{F}}_i^+, F_i$
and
${\mathcal{F}}_i^{\mathrm{ord}},{\mathcal{F}}_i^+, F_i$
and
![]() $V_i$
are defined.
$V_i$
are defined.
-
Inv1(i).
 $R({\mathcal{F}}_i^{\mathrm{ord}}) = R({\mathcal{F}}_i^+)=F_i$
,
$R({\mathcal{F}}_i^{\mathrm{ord}}) = R({\mathcal{F}}_i^+)=F_i$
,
 ${\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}}) \subseteq{\mathrm{In}}({\mathcal{F}}_i^+)$
, and
${\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}}) \subseteq{\mathrm{In}}({\mathcal{F}}_i^+)$
, and
 $E\setminus E(B_{r_1}(v))\subseteq F_i$
,
$E\setminus E(B_{r_1}(v))\subseteq F_i$
, -
Inv2(i). For all distinct
 $u_1, u_2\in V_i$
,
$u_1, u_2\in V_i$
,
 $V(T_{u_1})\cap V(T_{u_2}) = \emptyset$
,
$V(T_{u_1})\cap V(T_{u_2}) = \emptyset$
, -
Inv3(i).
 $\bigcup _{u\in V_i} V(T_u) = V(F_i)\cap V(T)$
and
$\bigcup _{u\in V_i} V(T_u) = V(F_i)\cap V(T)$
and
 $\bigcup _{u\in V_i} E(T_u) \subseteq F_i$
,
$\bigcup _{u\in V_i} E(T_u) \subseteq F_i$
, -
Inv4(i). If
 $d_G(F_i, v) \gt r_2$
, then
$d_G(F_i, v) \gt r_2$
, then
 $\partial _G (F_i)\subseteq V_i$
,
$\partial _G (F_i)\subseteq V_i$
, -
Inv5(i). If
 $F_{i+1}$
is defined, then
$F_{i+1}$
is defined, then
 $F_i \subset F_{i+1}$
, and
$F_i \subset F_{i+1}$
, and
-
Inv6(i). If
 ${\mathcal{F}}_{i+1}^{\mathrm{ord}}$
and
${\mathcal{F}}_{i+1}^{\mathrm{ord}}$
and
 ${\mathcal{F}}_{i+1}^+$
are defined in the process, then
${\mathcal{F}}_{i+1}^+$
are defined in the process, then
 ${\mathcal{F}}^{\mathrm{ord}}_i \subseteq{\mathcal{F}}^{\mathrm{ord}}_{i+1}$
and
${\mathcal{F}}^{\mathrm{ord}}_i \subseteq{\mathcal{F}}^{\mathrm{ord}}_{i+1}$
and
 ${\mathcal{F}}^+_i \subseteq{\mathcal{F}}^+_{i+1}$
${\mathcal{F}}^+_i \subseteq{\mathcal{F}}^+_{i+1}$
Proof. We do an induction on
![]() $i$
. For the base case let
$i$
. For the base case let
![]() $i = 0$
. Inv1(
$i = 0$
. Inv1(
![]() $0$
) holds by the definitions of
$0$
) holds by the definitions of
![]() $F_0$
,
$F_0$
,
![]() ${\mathcal{F}}_0^{\mathrm{ord}}$
and
${\mathcal{F}}_0^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}_0^+$
. Inv2(
${\mathcal{F}}_0^+$
. Inv2(
![]() $0$
) follows from the fact that any
$0$
) follows from the fact that any
![]() $u\in V_0$
is a leaf of
$u\in V_0$
is a leaf of
![]() $T$
and thus
$T$
and thus
![]() $T_u$
contains a single vertex -
$T_u$
contains a single vertex -
![]() $u$
.
$u$
.
The second part of Inv3(
![]() $0$
) is trivial as neither of the subtrees have any edges. We show the first part of Inv3(
$0$
) is trivial as neither of the subtrees have any edges. We show the first part of Inv3(
![]() $0$
) by proving that for all
$0$
) by proving that for all
![]() $u\in V(T)$
,
$u\in V(T)$
,
![]() $u\in V_0$
if and only if
$u\in V_0$
if and only if
![]() $u\in V(F_0)$
. First, suppose that
$u\in V(F_0)$
. First, suppose that
![]() $u\in V(F_0)\cap V(T)$
. The definitions of
$u\in V(F_0)\cap V(T)$
. The definitions of
![]() $F_0$
and
$F_0$
and
![]() $T$
imply that
$T$
imply that
![]() $d_G(u,v) = r_1$
so
$d_G(u,v) = r_1$
so
![]() $u\in V_0$
, as desired. For the other direction, consider
$u\in V_0$
, as desired. For the other direction, consider
![]() $u\in V_0$
. We need to show that
$u\in V_0$
. We need to show that
![]() $G$
has an edge
$G$
has an edge
![]() $\{u,u'\}$
with
$\{u,u'\}$
with
![]() $d_G(u',v) \gt r_1$
. The vertex
$d_G(u',v) \gt r_1$
. The vertex
![]() $u$
is a leaf of
$u$
is a leaf of
![]() $T$
, hence
$T$
, hence
![]() $u$
has a single incident edge in
$u$
has a single incident edge in
![]() $E(T)$
. Given that
$E(T)$
. Given that
![]() $G$
is
$G$
is
![]() $\Delta$
-regular with
$\Delta$
-regular with
![]() $\Delta \gt 1$
, there is some edge
$\Delta \gt 1$
, there is some edge
![]() $\{u, u'\}$
, such that
$\{u, u'\}$
, such that
![]() $u'$
is not
$u'$
is not
![]() $u$
’s parent in
$u$
’s parent in
![]() $T$
. By Observation32,
$T$
. By Observation32,
![]() $d_G(u', v) \in \{r_1 - 1, r_1, r_1 + 1\}$
. By the choice of
$d_G(u', v) \in \{r_1 - 1, r_1, r_1 + 1\}$
. By the choice of
![]() $r_1$
,
$r_1$
,
![]() $ r_2$
, and
$ r_2$
, and
![]() $u'$
,
$u'$
,
![]() $\{u, u'\} \notin E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
, so
$\{u, u'\} \notin E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
, so
![]() $d_G(u', v) = r_1 + 1 \gt r_1$
, and the result follows.
$d_G(u', v) = r_1 + 1 \gt r_1$
, and the result follows.
The invariant Inv4(
![]() $0$
) follows from the fact that for any
$0$
) follows from the fact that for any
![]() $u\in \partial _G (F_0)$
there are edges
$u\in \partial _G (F_0)$
there are edges
![]() $\{u, u_1\} \in F_0$
and
$\{u, u_1\} \in F_0$
and
![]() $\{u,u_2\}\notin F_0$
, so
$\{u,u_2\}\notin F_0$
, so
![]() $d_G(u, v) \leq r_1$
and
$d_G(u, v) \leq r_1$
and
![]() $d_G(u_2, v) \leq r_1$
, and thus also
$d_G(u_2, v) \leq r_1$
, and thus also
![]() $d_G(u_1, v) \gt r_1$
, so by Observation32 it follows that
$d_G(u_1, v) \gt r_1$
, so by Observation32 it follows that
![]() $d_G(u, v) = r_1$
and thus
$d_G(u, v) = r_1$
and thus
![]() $u\in V_0$
.
$u\in V_0$
.
For the inductive step, suppose
![]() $F_{i+1}$
,
$F_{i+1}$
,
![]() ${\mathcal{F}}_{i+1}^{\mathrm{ord}}$
,
${\mathcal{F}}_{i+1}^{\mathrm{ord}}$
,
![]() $F_{i+1}^+$
and
$F_{i+1}^+$
and
![]() $V_{i+1}$
are all defined and suppose that Inv1(
$V_{i+1}$
are all defined and suppose that Inv1(
![]() $i$
)-Inv4(
$i$
)-Inv4(
![]() $i$
) hold. We now show Inv5(
$i$
) hold. We now show Inv5(
![]() $i$
), Inv6(
$i$
), Inv6(
![]() $i$
) and Inv1(
$i$
) and Inv1(
![]() $i+1$
)–Inv4(
$i+1$
)–Inv4(
![]() $i+1$
).
$i+1$
).
For Inv5(
![]() $i$
),
$i$
),
![]() $F_{i}\subseteq F_{i+1}$
follows by construction. For the strict inequality, it is enough to show that
$F_{i}\subseteq F_{i+1}$
follows by construction. For the strict inequality, it is enough to show that
![]() $\{w_i, p_i\}\in F_{i+1}\setminus F_i$
. Since
$\{w_i, p_i\}\in F_{i+1}\setminus F_i$
. Since
![]() $F_{i+1}$
is defined,
$F_{i+1}$
is defined,
![]() $d_G(F_i, v) \gt r_2$
, otherwise the process would terminate before the
$d_G(F_i, v) \gt r_2$
, otherwise the process would terminate before the
![]() $(i+1)$
th iteration of Step 3. Thus by Inv4(
$(i+1)$
th iteration of Step 3. Thus by Inv4(
![]() $i$
) and by
$i$
) and by
![]() $w_i\in \partial _G (F_i)$
,
$w_i\in \partial _G (F_i)$
,
![]() $w_i\in V_i$
. So for any
$w_i\in V_i$
. So for any
![]() $u\in V_i$
, Inv2(
$u\in V_i$
, Inv2(
![]() $i$
) implies that
$i$
) implies that
![]() $p_i\notin V(T_u)$
. Hence Inv3(
$p_i\notin V(T_u)$
. Hence Inv3(
![]() $i$
) implies that
$i$
) implies that
![]() $p_i\notin V(F_i)$
so
$p_i\notin V(F_i)$
so
![]() $\{w_i, p_i\}\notin F_i$
. But
$\{w_i, p_i\}\notin F_i$
. But
![]() $E(T_{p_i})\subseteq F_{i+1}$
, hence
$E(T_{p_i})\subseteq F_{i+1}$
, hence
![]() $\{w_i, p_i\}\in F_{i+1}$
, completing the proof of Inv5(
$\{w_i, p_i\}\in F_{i+1}$
, completing the proof of Inv5(
![]() $i$
). Inv6(
$i$
). Inv6(
![]() $i$
) follows by construction.
$i$
) follows by construction.
The first and third parts of Inv1(
![]() $i+1$
) follow by construction, the second part follows from Corollary53 (see Appendix B, using
$i+1$
) follow by construction, the second part follows from Corollary53 (see Appendix B, using
![]() ${\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})\subseteq{\mathrm{In}}({\mathcal{F}}_i^+)$
and the fact that the coupling is optimal. Inv2(
${\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})\subseteq{\mathrm{In}}({\mathcal{F}}_i^+)$
and the fact that the coupling is optimal. Inv2(
![]() $i + 1$
) follows by construction and Inv2(
$i + 1$
) follows by construction and Inv2(
![]() $i$
). Also, the second part of Inv3(
$i$
). Also, the second part of Inv3(
![]() $i + 1$
) follows by construction and Inv3(
$i + 1$
) follows by construction and Inv3(
![]() $i$
).
$i$
).
For the first part of Inv3(
![]() $i+1$
), by the definition of
$i+1$
), by the definition of
![]() $F_{i+1}$
, if
$F_{i+1}$
, if
![]() $u\in V(F_{i+1})\cap V(T)$
, then
$u\in V(F_{i+1})\cap V(T)$
, then
![]() $u\in V(T_{p_i})$
or
$u\in V(T_{p_i})$
or
![]() $u\in V(F_{i})\cap V(T)$
. In the first case, note
$u\in V(F_{i})\cap V(T)$
. In the first case, note
![]() $p_i\in V_{i+1}$
. Otherwise, by Inv3(
$p_i\in V_{i+1}$
. Otherwise, by Inv3(
![]() $i$
), there is a vertex
$i$
), there is a vertex
![]() $u'\in V_i$
with
$u'\in V_i$
with
![]() $u\in V(T_{u'})$
. If
$u\in V(T_{u'})$
. If
![]() $u'$
is in
$u'$
is in
![]() $V(T_{p_i})$
, then so is
$V(T_{p_i})$
, then so is
![]() $u$
, hence the first case applies. If not, then
$u$
, hence the first case applies. If not, then
![]() $u'\in V_{i+1}$
. For the converse, for
$u'\in V_{i+1}$
. For the converse, for
![]() $u\in V_{i+1}$
, there are two cases. If
$u\in V_{i+1}$
, there are two cases. If
![]() $u = p_i$
then
$u = p_i$
then
![]() $E(T_{p_i})\subseteq F_{i+1}$
so
$E(T_{p_i})\subseteq F_{i+1}$
so
![]() $V(T_{p_i}) \subseteq V(F_{i+1})\cap V(T)$
. Otherwise,
$V(T_{p_i}) \subseteq V(F_{i+1})\cap V(T)$
. Otherwise,
![]() $u\in V_i$
, so the result follows by Inv3(
$u\in V_i$
, so the result follows by Inv3(
![]() $i$
) and Inv5(
$i$
) and Inv5(
![]() $i$
).
$i$
).
Finally we prove Inv4(
![]() $i+1$
). Suppose that
$i+1$
). Suppose that
![]() $d_G(F_{i+1}, v) \gt r_2$
and let
$d_G(F_{i+1}, v) \gt r_2$
and let
![]() $u\in \partial _G F_{i+1}$
. Our goal is to show
$u\in \partial _G F_{i+1}$
. Our goal is to show
![]() $u\in V_{i+1}$
Let
$u\in V_{i+1}$
Let
![]() $u_1, u_2\in V$
be such that
$u_1, u_2\in V$
be such that
![]() $\{u, u_1\}\in F_{i+1}$
and
$\{u, u_1\}\in F_{i+1}$
and
![]() $\{u, u_2\}\notin F_{i+1}$
. By Inv1(
$\{u, u_2\}\notin F_{i+1}$
. By Inv1(
![]() $i+1$
),
$i+1$
),
![]() $E\setminus E(B_{r_1}(v))\subseteq F_{i+1}$
, and so
$E\setminus E(B_{r_1}(v))\subseteq F_{i+1}$
, and so
![]() $u, u_2 \in V(B_{r_1}(v)) = V(T)$
. Also,
$u, u_2 \in V(B_{r_1}(v)) = V(T)$
. Also,
![]() $d_G(u, v) \gt r_2$
implies
$d_G(u, v) \gt r_2$
implies
![]() $\{u, u_2\}\in E(B_{r_1}(v))\setminus E(B_{r_2}(v)$
. Since
$\{u, u_2\}\in E(B_{r_1}(v))\setminus E(B_{r_2}(v)$
. Since
![]() $\{u, u_1\}\in F_{i+1}$
,
$\{u, u_1\}\in F_{i+1}$
,
![]() $u\in V(F_{i+1})$
, so by Inv3(
$u\in V(F_{i+1})$
, so by Inv3(
![]() $i+1$
), there is a vertex
$i+1$
), there is a vertex
![]() $u'\in V_{i+1}$
such that
$u'\in V_{i+1}$
such that
![]() $u\in V(T_{u'})$
. By the choice of
$u\in V(T_{u'})$
. By the choice of
![]() $r_1$
and
$r_1$
and
![]() $r_2$
,
$r_2$
,
![]() $\{u, u_2\}$
is a tree edge, so if
$\{u, u_2\}$
is a tree edge, so if
![]() $u\neq u'$
, by the second part of Inv3(
$u\neq u'$
, by the second part of Inv3(
![]() $i+1$
),
$i+1$
),
![]() $\{u, u_2\}$
would be then in
$\{u, u_2\}$
would be then in
![]() $F_{i+1}$
, contradicting the choice of
$F_{i+1}$
, contradicting the choice of
![]() $u_2$
. Thus
$u_2$
. Thus
![]() $u = u' \in V_{i+1}$
.
$u = u' \in V_{i+1}$
.
Observation 41.
The process eventually terminates, with
![]() ${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}_{r_1}^+(v)}$
.
${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}_{r_1}^+(v)}$
.
Proof. By Inv5, the process always terminates. If the process terminates in Step 1a, then, by construction, the resulting configurations are drawn from the correct distributions. Otherwise, Step 2 is executed. Thus,
![]() $(1-\eta ) |E| \leq |{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_0)|$
. By Inv6, for every value of
$(1-\eta ) |E| \leq |{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_0)|$
. By Inv6, for every value of
![]() $i$
until termination,
$i$
until termination,
![]() $(1-\eta ) |E| \leq |{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_0)| \leq |{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_i)|$
. This implies that every
$(1-\eta ) |E| \leq |{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_0)| \leq |{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_i)|$
. This implies that every
![]() $\Omega _{{\mathcal{F}}_i^{\mathrm{ord}}} \subseteq \Omega ^{\mathrm{ord}}$
so
$\Omega _{{\mathcal{F}}_i^{\mathrm{ord}}} \subseteq \Omega ^{\mathrm{ord}}$
so
![]() $\pi _{{\mathcal{F}}_i^{\mathrm{ord}}}^{\mathrm{ord}} = \pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
. From this it follows that
$\pi _{{\mathcal{F}}_i^{\mathrm{ord}}}^{\mathrm{ord}} = \pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
. From this it follows that
![]() ${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
. Given how
${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
. Given how
![]() ${\mathcal{F}}_0^+$
is generated in Step 1b, it holds that, for any
${\mathcal{F}}_0^+$
is generated in Step 1b, it holds that, for any
![]() ${\mathcal{F}}\in \Omega$
,
${\mathcal{F}}\in \Omega$
,
![]() $\pi _{{\mathcal{B}}_{r_1}^+(v)}({\mathcal{F}}) \gt 0$
precisely when
$\pi _{{\mathcal{B}}_{r_1}^+(v)}({\mathcal{F}}) \gt 0$
precisely when
![]() ${\mathcal{F}}_0^+\subseteq{\mathcal{F}}$
. Then
${\mathcal{F}}_0^+\subseteq{\mathcal{F}}$
. Then
![]() ${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}_{r_1}^+(v)}$
follows from the way that
${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}_{r_1}^+(v)}$
follows from the way that
![]() ${\mathcal{F}}^+_i$
is generated in the process.
${\mathcal{F}}^+_i$
is generated in the process.
Observation 42.
If the process terminates in Step 2a, then there is a non-negative integer
![]() $i$
such that
$i$
such that
![]() $G[{\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})]$
has a giant component containing all vertices in
$G[{\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})]$
has a giant component containing all vertices in
![]() $\partial _G(F_i)$
. Also,
$\partial _G(F_i)$
. Also,
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
agree on the edges that are incident to
${\mathcal{F}}^+$
agree on the edges that are incident to
![]() $v$
.
$v$
.
Proof. The only way that the process can get to Step 2a, with some index
![]() $i$
, is if
$i$
, is if
![]() $d_G(F_i, v) \gt r_2$
and
$d_G(F_i, v) \gt r_2$
and
![]() $W_i = \emptyset$
. In this case all vertices of the boundary
$W_i = \emptyset$
. In this case all vertices of the boundary
![]() $\partial _G(F_i)$
are contained in the giant component of
$\partial _G(F_i)$
are contained in the giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})]$
.
Since
![]() $r_2 \geq 0$
,
$r_2 \geq 0$
,
![]() $d_G(F_i, v) \gt r_2 \geq 0$
, so the edges that are incident to
$d_G(F_i, v) \gt r_2 \geq 0$
, so the edges that are incident to
![]() $v$
are not in
$v$
are not in
![]() $F_i$
. Since
$F_i$
. Since
![]() $G$
is connected, the boundary
$G$
is connected, the boundary
![]() $\partial _G (F_i)$
is non-empty.
$\partial _G (F_i)$
is non-empty.
Thus
![]() $\xi ({\mathcal{F}}_{i}^{\mathrm{ord}})$
consists of a single equivalence class containing all vertices of
$\xi ({\mathcal{F}}_{i}^{\mathrm{ord}})$
consists of a single equivalence class containing all vertices of
![]() $\partial _G(F_i)$
. By Inv1(
$\partial _G(F_i)$
. By Inv1(
![]() $i$
),
$i$
),
![]() ${\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})\subseteq{\mathrm{In}}({\mathcal{F}}_i^+)$
and
${\mathrm{In}}({\mathcal{F}}_i^{\mathrm{ord}})\subseteq{\mathrm{In}}({\mathcal{F}}_i^+)$
and
![]() $R({\mathcal{F}}_i^{\mathrm{ord}}) = R({\mathcal{F}}_i^+)$
, so
$R({\mathcal{F}}_i^{\mathrm{ord}}) = R({\mathcal{F}}_i^+)$
, so
![]() $G[{\mathrm{In}}({\mathcal{F}}_i^+)]$
has a giant component containing all vertices in
$G[{\mathrm{In}}({\mathcal{F}}_i^+)]$
has a giant component containing all vertices in
![]() $\partial _G(F_i)$
and
$\partial _G(F_i)$
and
![]() $\xi ({\mathcal{F}}_i^+)$
contains a single equivalence class, containing all vetices in
$\xi ({\mathcal{F}}_i^+)$
contains a single equivalence class, containing all vetices in
![]() $\partial _G(F_i)$
. By Observation51,
$\partial _G(F_i)$
. By Observation51,
![]() $\pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
and
$\pi _{{\mathcal{F}}_i^{\mathrm{ord}}}$
and
![]() $\pi _{{\mathcal{F}}_i^+}$
have the same projection on
$\pi _{{\mathcal{F}}_i^+}$
have the same projection on
![]() $E\backslash F_i$
, meaning that for any partial configuration
$E\backslash F_i$
, meaning that for any partial configuration
![]() ${\mathcal{A}}\in \Omega _{E\backslash F_i}$
,
${\mathcal{A}}\in \Omega _{E\backslash F_i}$
,
![]() $\pi _{{\mathcal{F}}_i^{\mathrm{ord}}}({\mathcal{F}}_i^{\mathrm{ord}} \cup{\mathcal{A}}) = \pi _{{\mathcal{F}}_i^+}({\mathcal{F}}_i^+ \cup{\mathcal{A}})$
. Since the coupling in Step 2a is optimal,
$\pi _{{\mathcal{F}}_i^{\mathrm{ord}}}({\mathcal{F}}_i^{\mathrm{ord}} \cup{\mathcal{A}}) = \pi _{{\mathcal{F}}_i^+}({\mathcal{F}}_i^+ \cup{\mathcal{A}})$
. Since the coupling in Step 2a is optimal,
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
agree on the edges incident to
${\mathcal{F}}^+$
agree on the edges incident to
![]() $v$
(since they are not in
$v$
(since they are not in
![]() $F_i$
).
$F_i$
).
Observation 43.
Suppose that Step 2a is executed with index
![]() $i$
and let
$i$
and let
![]() $k = r_1 - d_G(w_i, v)$
. There are non-negative integers
$k = r_1 - d_G(w_i, v)$
. There are non-negative integers
![]() $j_0,\ldots, j_k$
with
$j_0,\ldots, j_k$
with
![]() $j_k=i$
such that, for every
$j_k=i$
such that, for every
![]() $\ell \in \{0,\ldots, k-1\}$
,
$\ell \in \{0,\ldots, k-1\}$
,
![]() $j_{\ell } \lt j_{\ell +1}$
and
$j_{\ell } \lt j_{\ell +1}$
and
![]() $w_{j_{\ell +1}} = p_{j_\ell }$
.
$w_{j_{\ell +1}} = p_{j_\ell }$
.
Proof. By construction,
![]() $w_i\in \partial _G(F_i)$
and
$w_i\in \partial _G(F_i)$
and
![]() $d_G(F_i,v) \gt r_2$
. By Inv4(
$d_G(F_i,v) \gt r_2$
. By Inv4(
![]() $i$
),
$i$
),
![]() $\partial _G(F_i) \subseteq V_i\subseteq V(T)$
. Hence
$\partial _G(F_i) \subseteq V_i\subseteq V(T)$
. Hence
![]() $d_G(w_i, v) \leq r_1$
, so
$d_G(w_i, v) \leq r_1$
, so
![]() $k \geq 0$
. The proof is by induction on
$k \geq 0$
. The proof is by induction on
![]() $k$
.
$k$
.
For the base case,
![]() $k = 0$
, it suffices to define
$k = 0$
, it suffices to define
![]() $j_0 \;:\!=\; i$
and the condition in the statement of the observation is vacuous.
$j_0 \;:\!=\; i$
and the condition in the statement of the observation is vacuous.
For the induction step, fix
![]() $k\geq 0$
and assume that the observation holds whenever Step 2a is executed with any index
$k\geq 0$
and assume that the observation holds whenever Step 2a is executed with any index
![]() $j$
such that
$j$
such that
![]() $r_1 - d_G(w_j, v)\leq k$
. Suppose that Step 2a is executed with index
$r_1 - d_G(w_j, v)\leq k$
. Suppose that Step 2a is executed with index
![]() $i$
such that
$i$
such that
![]() $r_1 - d_G(w_i, v) = k+1$
. Define
$r_1 - d_G(w_i, v) = k+1$
. Define
![]() $j_{k+1} \;:\!=\; i$
. By Invariant Inv4(
$j_{k+1} \;:\!=\; i$
. By Invariant Inv4(
![]() $i$
),
$i$
),
![]() $w_i\in V_i$
. By the construction of
$w_i\in V_i$
. By the construction of
![]() $V_i$
, either
$V_i$
, either
![]() $d_G(w_i, v) = r_1$
, or there is an index
$d_G(w_i, v) = r_1$
, or there is an index
![]() $i'\lt i$
such that
$i'\lt i$
such that
![]() $w_i = p_{i'}$
. The first case is ruled out by
$w_i = p_{i'}$
. The first case is ruled out by
![]() $d_G(w_i, v) = r_1 - (k+1) \lt r_1$
. In the second case,
$d_G(w_i, v) = r_1 - (k+1) \lt r_1$
. In the second case,
![]() $w_i$
is the parent of
$w_i$
is the parent of
![]() $w_{i'}$
in the BFS tree, so
$w_{i'}$
in the BFS tree, so
![]() $d_G(w_{i'}, v) = d_G(w_i, v) + 1$
and
$d_G(w_{i'}, v) = d_G(w_i, v) + 1$
and
![]() $k= r_1 - d_G(w_{i'},v)$
. We finish by applying the inductive hypothesis with index
$k= r_1 - d_G(w_{i'},v)$
. We finish by applying the inductive hypothesis with index
![]() $i'$
.
$i'$
.
Equipped with these results, we can now prove the following lemma.
Lemma 44.
Fix
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K, M\gt 0$
. Suppose that
$K, M\gt 0$
. Suppose that
![]() $\beta \geq 3 M$
. Suppose that
$\beta \geq 3 M$
. Suppose that
![]() $n$
is sufficiently large so that
$n$
is sufficiently large so that
![]() $r\;:\!=\; \tfrac{M}\beta \log _{\Delta -1} n \gt K$
. and
$r\;:\!=\; \tfrac{M}\beta \log _{\Delta -1} n \gt K$
. and
![]() $|B_{r}(v)| \leq 9 \Delta n/200$
. Define
$|B_{r}(v)| \leq 9 \Delta n/200$
. Define
![]() $r_1$
as in Observation
33
so that
$r_1$
as in Observation
33
so that
![]() $r_1\geq \frac{r}{K+1}-1$
. Let
$r_1\geq \frac{r}{K+1}-1$
. Let
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
be generated by the process. Then at least one of the following conditions holds.
${\mathcal{F}}^+$
be generated by the process. Then at least one of the following conditions holds.
-
1.
 ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
 ${\mathcal{F}}^+$
agree on the edges that are incident to
${\mathcal{F}}^+$
agree on the edges that are incident to
 $v$
.
$v$
. -
2.
 $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus E(B_{r_1}(v))| \lt (1-\eta ) |E|$
.
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus E(B_{r_1}(v))| \lt (1-\eta ) |E|$
. -
3.
 ${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
 $\frac{r}{400\Delta (1+K)}-1$
.
$\frac{r}{400\Delta (1+K)}-1$
.
Proof. By Observation41, the process eventually terminates. If it terminates in Step 1a, then
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus E(B_{r_1}(v))| \lt (1-\eta )|E|$
, thus Condition 2 is satisfied. If the process terminates in Step 2a, then by Observation42, Condition 1 holds.
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus E(B_{r_1}(v))| \lt (1-\eta )|E|$
, thus Condition 2 is satisfied. If the process terminates in Step 2a, then by Observation42, Condition 1 holds.
For the rest of the proof we assume that the process terminates in Step 3. We will show that Condition 3 holds. Let
![]() $i'$
be the index that triggers the condition
$i'$
be the index that triggers the condition
![]() $d_G(F_{i'}, v) \leq r_2$
in Step 2. Let
$d_G(F_{i'}, v) \leq r_2$
in Step 2. Let
![]() $i \;:\!=\; i' - 1$
so that step 2a is run for the last time with index
$i \;:\!=\; i' - 1$
so that step 2a is run for the last time with index
![]() $i$
. By the choice of
$i$
. By the choice of
![]() $i'$
,
$i'$
,
![]() $d_G(F_i, v) \gt r_2$
. Since
$d_G(F_i, v) \gt r_2$
. Since
![]() $p_{i}$
is an endpoint of an edge in
$p_{i}$
is an endpoint of an edge in
![]() $F_{i'}$
,
$F_{i'}$
,
![]() $d_G(p_i,v) \leq r_2$
. Since
$d_G(p_i,v) \leq r_2$
. Since
![]() $w_i\in \partial _G(F_i)$
,
$w_i\in \partial _G(F_i)$
,
![]() $d_G(v,w_i) \gt r_2$
. Since
$d_G(v,w_i) \gt r_2$
. Since
![]() $d_G(w_i, v) = d_G(p_i, v) + 1$
, we conclude that
$d_G(w_i, v) = d_G(p_i, v) + 1$
, we conclude that
![]() $d_G(w_i, v) = r_2 + 1$
. By Observation43 with index
$d_G(w_i, v) = r_2 + 1$
. By Observation43 with index
![]() $i$
and
$i$
and
![]() $k = r_1 - (r_2+1)$
, there are non-negative integers
$k = r_1 - (r_2+1)$
, there are non-negative integers
![]() $\{j_0,\ldots, j_k\}$
with
$\{j_0,\ldots, j_k\}$
with
![]() $j_k=i$
such that, for every
$j_k=i$
such that, for every
![]() $\ell \in \{0,\ldots, k-1\}$
,
$\ell \in \{0,\ldots, k-1\}$
,
![]() $j_\ell \lt j_{\ell +1}$
and
$j_\ell \lt j_{\ell +1}$
and
![]() $p_{j_\ell } = w_{j_{\ell +1}}$
. Thus
$p_{j_\ell } = w_{j_{\ell +1}}$
. Thus
![]() $w_{j_{\ell +1}} \in V_{\ell +1}$
. Note that
$w_{j_{\ell +1}} \in V_{\ell +1}$
. Note that
![]() $w_{j_0},\ldots, w_{j_k}$
is a path in
$w_{j_0},\ldots, w_{j_k}$
is a path in
![]() $T$
and that
$T$
and that
![]() $w_{j_k}$
is closest to the root
$w_{j_k}$
is closest to the root
![]() $v$
in this path. By Observation33 and the definition of
$v$
in this path. By Observation33 and the definition of
![]() $k$
,
$k$
,
![]() $k \geq r/(K+1)-2$
. Let
$k \geq r/(K+1)-2$
. Let
![]() $r' = \lfloor k / 2\rfloor$
,
$r' = \lfloor k / 2\rfloor$
,
![]() $J' = \{j_{\ell } \mid r' \leq \ell \leq k\}$
and
$J' = \{j_{\ell } \mid r' \leq \ell \leq k\}$
and
![]() $W' = \{w_j \mid j\in J'\}$
. Since
$W' = \{w_j \mid j\in J'\}$
. Since
![]() $V(T) \subseteq V(B_{r+1}(v))$
, we have established that for all
$V(T) \subseteq V(B_{r+1}(v))$
, we have established that for all
![]() $w\in W'$
$w\in W'$
![]() $r_2+1 \leq d_G(v,w) \leq r_1$
. We now distinguish three cases.
$r_2+1 \leq d_G(v,w) \leq r_1$
. We now distinguish three cases.
Case 1. For all
![]() $j\in J'$
,
$j\in J'$
,
![]() $w_j$
is not in a giant component of
$w_j$
is not in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
.
Let
![]() $F'$
be the set of edges with endpoints in
$F'$
be the set of edges with endpoints in
![]() $W'$
and note that
$W'$
and note that
![]() $F'$
contains the edges in the path
$F'$
contains the edges in the path
![]() $w_{r'},\ldots, w_{k}$
. By Observation41,
$w_{r'},\ldots, w_{k}$
. By Observation41,
![]() ${\mathcal{F}}^{\mathrm{ord}} \in \Omega ^{\mathrm{ord}}$
. Applying Item 1 of Lemma29 to each vertex
${\mathcal{F}}^{\mathrm{ord}} \in \Omega ^{\mathrm{ord}}$
. Applying Item 1 of Lemma29 to each vertex
![]() $u\in W'$
, we find that every edge in
$u\in W'$
, we find that every edge in
![]() $F'$
is contained in a polymer of
$F'$
is contained in a polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
. Since the vertices in
${\mathcal{F}}^{\mathrm{ord}}$
. Since the vertices in
![]() $W'$
form a path in
$W'$
form a path in
![]() $G$
, the edges in
$G$
, the edges in
![]() $F'$
are all in the same polymer of
$F'$
are all in the same polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
. Thus,
${\mathcal{F}}^{\mathrm{ord}}$
. Thus,
![]() ${\mathcal{F}}^{\mathrm{ord}}$
has a polymer of size at least
${\mathcal{F}}^{\mathrm{ord}}$
has a polymer of size at least
![]() $k/2 \geq r/(2(K+1))-1$
.
$k/2 \geq r/(2(K+1))-1$
.
Case 2. There is an index
![]() $j \in J'$
such that
$j \in J'$
such that
![]() $w_j$
is in the giant component of
$w_j$
is in the giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
and the giant component of
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
and the giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j, p_j\}]$
.
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j, p_j\}]$
.
We make the following claim.
Claim 2a: There is then a non-empty set
![]() $S$
of at most
$S$
of at most
![]() $9 \Delta |V|/200$
edges of
$9 \Delta |V|/200$
edges of
![]() $G$
such that the size of the component
$G$
such that the size of the component
![]() $\kappa '$
of
$\kappa '$
of
![]() $w_j$
in the graph
$w_j$
in the graph
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash S]$
is less than
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash S]$
is less than
![]() $n/2$
and furthermore
$n/2$
and furthermore
![]() $|V(\kappa ')| \geq |S|r'$
.
$|V(\kappa ')| \geq |S|r'$
.
Before proving Claim 2a, we show that it implies Condition 3, completing the proof of Case 2. By Lemma29, item 2, all but at most
![]() $45\Delta |S|$
vertices of
$45\Delta |S|$
vertices of
![]() $\kappa '$
are such that all their incident edges belong to polymer. Thus, at least
$\kappa '$
are such that all their incident edges belong to polymer. Thus, at least
![]() $|S|r' - 45\Delta |S|$
vertices of
$|S|r' - 45\Delta |S|$
vertices of
![]() $\kappa '$
are such that all their incident edges are in a polymer. By Lemma29, item 3, there are at most
$\kappa '$
are such that all their incident edges are in a polymer. By Lemma29, item 3, there are at most
![]() $50\Delta ^2|S|$
polymers of
$50\Delta ^2|S|$
polymers of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
containing vertices of
${\mathcal{F}}^{\mathrm{ord}}$
containing vertices of
![]() $\kappa '$
. We conclude that there is a polymer of
$\kappa '$
. We conclude that there is a polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
containing at least
${\mathcal{F}}^{\mathrm{ord}}$
containing at least
![]() $\frac{|S|r' - 45\Delta |S|}{50\Delta ^2|S|}$
vertices of
$\frac{|S|r' - 45\Delta |S|}{50\Delta ^2|S|}$
vertices of
![]() $\kappa '$
with the property that all of their incident edges are in the polymer.
$\kappa '$
with the property that all of their incident edges are in the polymer.
Since the number of edges incident to a set of size
![]() $z$
is at least
$z$
is at least
![]() $\Delta z/2$
, there is a polymer of
$\Delta z/2$
, there is a polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
containing a vertex of
${\mathcal{F}}^{\mathrm{ord}}$
containing a vertex of
![]() $B_{r_1}(v)$
with size at least
$B_{r_1}(v)$
with size at least
To conclude the proof of Case 2, we prove Claim 2a. Since the process ends in Step 3, Step 1a does not occur, so
![]() $|{\mathrm{In}}(F^{\mathrm{ord}}_0)|\geq (1-\eta )|E|$
. Since
$|{\mathrm{In}}(F^{\mathrm{ord}}_0)|\geq (1-\eta )|E|$
. Since
![]() ${\mathcal{F}}^{{\mathrm{ord}}}_0\subseteq{\mathcal{F}}^{\mathrm{ord}}_j$
from Inv6,
${\mathcal{F}}^{{\mathrm{ord}}}_0\subseteq{\mathcal{F}}^{\mathrm{ord}}_j$
from Inv6,
![]() ${\mathrm{In}}(F^{{\mathrm{ord}}}_0)\subseteq{\mathrm{In}}(F^{\mathrm{ord}}_j)$
, so
${\mathrm{In}}(F^{{\mathrm{ord}}}_0)\subseteq{\mathrm{In}}(F^{\mathrm{ord}}_j)$
, so
![]() $|{\mathrm{In}}(F^{\mathrm{ord}}_j)|\geq (1-\eta )|E|$
. By Corollary20,
$|{\mathrm{In}}(F^{\mathrm{ord}}_j)|\geq (1-\eta )|E|$
. By Corollary20,
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_j)]$
has a (unique) giant component. Call this component
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}}_j)]$
has a (unique) giant component. Call this component
![]() $\kappa _j$
. Similarly,
$\kappa _j$
. Similarly,
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
has a giant component, call this component
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
has a giant component, call this component
![]() $\kappa$
. Note that
$\kappa$
. Note that
![]() $V(\kappa _j)\subseteq V(\kappa )$
. Since
$V(\kappa _j)\subseteq V(\kappa )$
. Since
![]() $w_j$
was chosen in Step 2a,
$w_j$
was chosen in Step 2a,
![]() $w_j\in V(\kappa )\backslash V(\kappa _j)$
.
$w_j\in V(\kappa )\backslash V(\kappa _j)$
.
Let
![]() $\Gamma$
be the set of all paths from
$\Gamma$
be the set of all paths from
![]() $w_j$
to
$w_j$
to
![]() $V(\kappa _j)$
in the graph
$V(\kappa _j)$
in the graph
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
. Every path
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
. Every path
![]() $\gamma \in \Gamma$
contains an edge in
$\gamma \in \Gamma$
contains an edge in
![]() $E\setminus F_j$
. Let
$E\setminus F_j$
. Let
![]() $\{u_1^\gamma, u_2^\gamma \}$
be the first such edge in
$\{u_1^\gamma, u_2^\gamma \}$
be the first such edge in
![]() $\gamma$
, with
$\gamma$
, with
![]() $d_G(u_1^\gamma, w_j) \lt d_G(u_2^\gamma, w_j)$
. Let
$d_G(u_1^\gamma, w_j) \lt d_G(u_2^\gamma, w_j)$
. Let
![]() $S\;:\!=\; \{ \{u_1^\gamma, u_2^\gamma \} \mid \gamma \in \Gamma \}$
.
$S\;:\!=\; \{ \{u_1^\gamma, u_2^\gamma \} \mid \gamma \in \Gamma \}$
.
By the definition of
![]() $S$
, any path from
$S$
, any path from
![]() $w_j$
to
$w_j$
to
![]() $\kappa _j$
goes through an edge in
$\kappa _j$
goes through an edge in
![]() $S$
, thus
$S$
, thus
![]() $w_j$
is not connected to
$w_j$
is not connected to
![]() $\kappa _j$
in
$\kappa _j$
in
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus S]$
. Let
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus S]$
. Let
![]() $\kappa '$
be the component of
$\kappa '$
be the component of
![]() $w_j$
in
$w_j$
in
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus S]$
. The component
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus S]$
. The component
![]() $\kappa '$
contains no vertices of
$\kappa '$
contains no vertices of
![]() $\kappa _j$
. Since
$\kappa _j$
. Since
![]() $|V(\kappa _j)|\gt n/2$
, we get
$|V(\kappa _j)|\gt n/2$
, we get
![]() $|V(\kappa ')| \lt n/2$
.
$|V(\kappa ')| \lt n/2$
.
We conclude by we proving that
![]() $|V(\kappa ')\cap B_{r_1}(v)|\geq |S|r'$
. The proof follows from a sequence of claims.
$|V(\kappa ')\cap B_{r_1}(v)|\geq |S|r'$
. The proof follows from a sequence of claims.
Claim 2b: For any
![]() $\gamma \in \Gamma$
,
$\gamma \in \Gamma$
,
![]() $u_1^\gamma \in \partial _G(F_j)$
and
$u_1^\gamma \in \partial _G(F_j)$
and
![]() $d_G(v,u_1^\gamma ) \gt r_2$
.
$d_G(v,u_1^\gamma ) \gt r_2$
.
The proof of Claim 2b is as follows. If
![]() $u_1^\gamma = w_j$
, then
$u_1^\gamma = w_j$
, then
![]() $u_1^\gamma \in \partial _G(F_j)$
by the choice of
$u_1^\gamma \in \partial _G(F_j)$
by the choice of
![]() $w_j$
. Otherwise, since
$w_j$
. Otherwise, since
![]() $u_1^\gamma$
is the first edge on
$u_1^\gamma$
is the first edge on
![]() $\gamma$
that is not in
$\gamma$
that is not in
![]() $E\setminus F_j$
, the edges on the path from
$E\setminus F_j$
, the edges on the path from
![]() $w_j$
to
$w_j$
to
![]() $u_1^\gamma$
are in
$u_1^\gamma$
are in
![]() $F_j$
, so there is a at least one edge from
$F_j$
, so there is a at least one edge from
![]() $F_j$
incident to
$F_j$
incident to
![]() $u_1^\gamma$
, and the edge
$u_1^\gamma$
, and the edge
![]() $\{u_1^\gamma, u_2^\gamma \}\notin F_j$
is also incident to
$\{u_1^\gamma, u_2^\gamma \}\notin F_j$
is also incident to
![]() $u_1^\gamma$
, so
$u_1^\gamma$
, so
![]() $u_1^\gamma \in \partial _G(F_j)$
. In either case,
$u_1^\gamma \in \partial _G(F_j)$
. In either case,
![]() $d_G(v,u_1^\gamma ) \geq d_G(v,F_j)\gt r_2$
.
$d_G(v,u_1^\gamma ) \geq d_G(v,F_j)\gt r_2$
.
Claim 2c: For any
![]() $\gamma \in \Gamma$
,
$\gamma \in \Gamma$
,
![]() $d_G(v,u_1^\gamma ) \leq r_1$
,
$d_G(v,u_1^\gamma ) \leq r_1$
,
![]() $d_G(v,u_2^\gamma ) \leq r_1$
,
$d_G(v,u_2^\gamma ) \leq r_1$
,
![]() $u_1^\gamma \in V_j$
, and
$u_1^\gamma \in V_j$
, and
![]() $u_2^\gamma$
is the parent of
$u_2^\gamma$
is the parent of
![]() $u_1^\gamma$
in
$u_1^\gamma$
in
![]() $V(T)$
$V(T)$
To prove Claim 2c, consider
![]() $\gamma \in \Gamma$
. Since the edge
$\gamma \in \Gamma$
. Since the edge
![]() $\{u_1^\gamma, u_2^\gamma \} \in E\setminus F_j$
, both
$\{u_1^\gamma, u_2^\gamma \} \in E\setminus F_j$
, both
![]() $u_1^\gamma$
and
$u_1^\gamma$
and
![]() $u_2^\gamma$
are in
$u_2^\gamma$
are in
![]() $V(B_{r_1}(v))=V(T)$
. Since Step 2 is executed with index
$V(B_{r_1}(v))=V(T)$
. Since Step 2 is executed with index
![]() $j$
,
$j$
,
![]() $d_G(F_j,v) \gt r_2$
. So by Claim 2b and Inv4(
$d_G(F_j,v) \gt r_2$
. So by Claim 2b and Inv4(
![]() $j$
),
$j$
),
![]() $u_1^\gamma \in V_j$
. By Invariant Inv3(
$u_1^\gamma \in V_j$
. By Invariant Inv3(
![]() $j$
),
$j$
),
![]() $E(T_{u_1^\gamma })\subseteq F_j$
, so the only candidate for
$E(T_{u_1^\gamma })\subseteq F_j$
, so the only candidate for
![]() $u_2^\gamma$
is the parent of
$u_2^\gamma$
is the parent of
![]() $u_1^\gamma$
in
$u_1^\gamma$
in
![]() $T$
.
$T$
.
Claim 2d:
![]() $|S| = |\{u_1^\gamma \mid \gamma \in \Gamma \}|$
.
$|S| = |\{u_1^\gamma \mid \gamma \in \Gamma \}|$
.
By Claim 2c, the mapping of a vertex
![]() $u \in \{u_1^\gamma \mid \gamma \in \Gamma \}$
to its parental edge in
$u \in \{u_1^\gamma \mid \gamma \in \Gamma \}$
to its parental edge in
![]() $T$
is a bijection between
$T$
is a bijection between
![]() $ \{u_1^\gamma \mid \gamma \in \Gamma \}$
and
$ \{u_1^\gamma \mid \gamma \in \Gamma \}$
and
![]() $S= \{ \{u_1^\gamma, u_2^\gamma \} \mid \gamma \in \Gamma \}$
.
$S= \{ \{u_1^\gamma, u_2^\gamma \} \mid \gamma \in \Gamma \}$
.
Claim 2e: For any
![]() $\gamma \in \Gamma$
,
$\gamma \in \Gamma$
,
![]() $|V(\kappa ')\cap V(T_{u_1^\gamma })| \geq r'$
.
$|V(\kappa ')\cap V(T_{u_1^\gamma })| \geq r'$
.
To prove Claim 2e, consider
![]() $\gamma \in \Gamma$
. We consider two cases. First, suppose
$\gamma \in \Gamma$
. We consider two cases. First, suppose
![]() $u_1^\gamma \neq w_j$
. By construction
$u_1^\gamma \neq w_j$
. By construction
![]() $w_j \in V_j$
and from Claim 2c,
$w_j \in V_j$
and from Claim 2c,
![]() $u_1^\gamma \in V_j$
. By Inv2(
$u_1^\gamma \in V_j$
. By Inv2(
![]() $j$
),
$j$
),
![]() $V(T_{w_j})\cap V(T_{u_1^\gamma }) = \emptyset$
. At the beginning of the proof, we established
$V(T_{w_j})\cap V(T_{u_1^\gamma }) = \emptyset$
. At the beginning of the proof, we established
![]() $r_2+1 \leq d_G(v,w_j) \leq r_1$
. By Claims 2b and 2c,
$r_2+1 \leq d_G(v,w_j) \leq r_1$
. By Claims 2b and 2c,
![]() $r_2 + 1 \leq d_G(v,u_1^\gamma ) \leq r_1$
. Since the path
$r_2 + 1 \leq d_G(v,u_1^\gamma ) \leq r_1$
. Since the path
![]() $\gamma$
goes from
$\gamma$
goes from
![]() $w_j$
to
$w_j$
to
![]() $u_1^\gamma$
without leaving
$u_1^\gamma$
without leaving
![]() $F_j$
, it goes from
$F_j$
, it goes from
![]() $w_j$
to a leaf of
$w_j$
to a leaf of
![]() $T_{w_j}$
and it finishes by going from a leaf of
$T_{w_j}$
and it finishes by going from a leaf of
![]() $T_{u_1^\gamma }$
to
$T_{u_1^\gamma }$
to
![]() $u_1^\gamma$
. All of these edges are in
$u_1^\gamma$
. All of these edges are in
![]() $\kappa '$
and there are at least
$\kappa '$
and there are at least
![]() $r_1 - d_G(v,u_1^\gamma )$
of them. Since, by Claim 2b,
$r_1 - d_G(v,u_1^\gamma )$
of them. Since, by Claim 2b,
![]() $u_1^\gamma \in \partial _G(F_j)$
but, by construction, it is not in
$u_1^\gamma \in \partial _G(F_j)$
but, by construction, it is not in
![]() $\kappa _j$
, by the definition of
$\kappa _j$
, by the definition of
![]() $W_j$
,
$W_j$
,
![]() $u_1^\gamma \in W_j$
. By the choice of
$u_1^\gamma \in W_j$
. By the choice of
![]() $w_j$
,
$w_j$
,
![]() $d_G(u_1^\gamma, v) \leq d_G(w_j, v) \leq r_1 - r'$
. Thus
$d_G(u_1^\gamma, v) \leq d_G(w_j, v) \leq r_1 - r'$
. Thus
![]() $|V(\kappa ')\cap V(T_{u_1^\gamma })|\geq r_1 - (r_1 - r') = r'$
.
$|V(\kappa ')\cap V(T_{u_1^\gamma })|\geq r_1 - (r_1 - r') = r'$
.
For the second case, suppose
![]() $u_1^\gamma = w_j$
. By the assumption of Case 2,
$u_1^\gamma = w_j$
. By the assumption of Case 2,
![]() $w_j$
is in a giant component of
$w_j$
is in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j, p_j\}]$
, thus
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j, p_j\}]$
, thus
![]() $S$
contains an edge other than the edge
$S$
contains an edge other than the edge
![]() $\{u_1^{\gamma '},u_2^{\gamma '}\}$
with
$\{u_1^{\gamma '},u_2^{\gamma '}\}$
with
![]() $\gamma ' \in \Gamma$
that is not equal to the edge
$\gamma ' \in \Gamma$
that is not equal to the edge
![]() $\{w_j,p_j\}$
. By Claim 2c,
$\{w_j,p_j\}$
. By Claim 2c,
![]() $u_1^{\gamma '} \neq w_j$
. Applying the argument from the first case to
$u_1^{\gamma '} \neq w_j$
. Applying the argument from the first case to
![]() $\gamma '$
, the path
$\gamma '$
, the path
![]() $\gamma '$
starts by going from
$\gamma '$
starts by going from
![]() $w_j$
to a leaf of
$w_j$
to a leaf of
![]() $T_{w_j}$
so it contains at least
$T_{w_j}$
so it contains at least
![]() $r'$
edges of
$r'$
edges of
![]() $T_{w_j}$
, all of which are in
$T_{w_j}$
, all of which are in
![]() $\kappa _j$
.
$\kappa _j$
.
We now use Claims 2d and 2e to finish the proof that
![]() $|V(\kappa ')| \geq |S| r'$
, which completes the proof of Claim 2a, and hence the proof of Case 2. Consider paths
$|V(\kappa ')| \geq |S| r'$
, which completes the proof of Claim 2a, and hence the proof of Case 2. Consider paths
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma '$
in
$\gamma '$
in
![]() $\Gamma$
with
$\Gamma$
with
![]() $u_1^\gamma \neq u_1^{\gamma '}$
. By Inv2(
$u_1^\gamma \neq u_1^{\gamma '}$
. By Inv2(
![]() $j$
),
$j$
),
![]() $V(T_{u_1^\gamma })\cap V(T_{u_1^{\gamma '}})=\emptyset$
, therefore
$V(T_{u_1^\gamma })\cap V(T_{u_1^{\gamma '}})=\emptyset$
, therefore
![]() $|V(\kappa ')| \geq \sum _{u\in \{u_1^\gamma \mid \gamma \in \Gamma \}} |V(\kappa ')\cap V(T_{u_1^\gamma })|$
. Claim 2e shows that each term in the sum is at least
$|V(\kappa ')| \geq \sum _{u\in \{u_1^\gamma \mid \gamma \in \Gamma \}} |V(\kappa ')\cap V(T_{u_1^\gamma })|$
. Claim 2e shows that each term in the sum is at least
![]() $r'$
. Claim 2d shows that
$r'$
. Claim 2d shows that
![]() $|S|$
is equal to the number of terms in the sum. Therefore we obtain
$|S|$
is equal to the number of terms in the sum. Therefore we obtain
![]() $|V(\kappa ')| \geq |S| r'$
, as required.
$|V(\kappa ')| \geq |S| r'$
, as required.
Case 3. There is an index
![]() $j \in J'$
such that
$j \in J'$
such that
![]() $w_j$
is in the giant component of
$w_j$
is in the giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
. However, for all
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
. However, for all
![]() $j\in J'$
,
$j\in J'$
,
![]() $w_j$
is not in a giant component of
$w_j$
is not in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j, p_j\}]$
.
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j, p_j\}]$
.
Let
![]() $\kappa$
be the giant component of
$\kappa$
be the giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
. Let
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
. Let
![]() $j_\ell = \min \{j \in J' \mid w_j \in V(\kappa )\}$
.
$j_\ell = \min \{j \in J' \mid w_j \in V(\kappa )\}$
.
Claim 3: For each
![]() $\ell '$
satisfying
$\ell '$
satisfying
![]() $\ell \leq \ell ' \lt k$
,
$\ell \leq \ell ' \lt k$
,
![]() $w_{j_{\ell '}}\in V(\kappa )$
and
$w_{j_{\ell '}}\in V(\kappa )$
and
![]() $\{w_{j_{\ell '}},w_{j_{\ell '+1}}\} \in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
.
$\{w_{j_{\ell '}},w_{j_{\ell '+1}}\} \in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
.
We prove Claim 3 by induction on
![]() $\ell '$
. The base case is
$\ell '$
. The base case is
![]() $\ell ' = \ell$
. In this case,
$\ell ' = \ell$
. In this case,
![]() $w_{j_{\ell }}\in V(\kappa )$
is from the definition of
$w_{j_{\ell }}\in V(\kappa )$
is from the definition of
![]() $j_\ell$
. Then since
$j_\ell$
. Then since
![]() $w_{j_\ell }$
is in a giant component of
$w_{j_\ell }$
is in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
but is not in a giant component of
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
but is not in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash \{w_{j_\ell }, p_{j_{\ell }}\}]$
, the edge
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash \{w_{j_\ell }, p_{j_{\ell }}\}]$
, the edge
![]() $\{w_{j_\ell }, p_{j_{\ell }}\} = \{w_{j_\ell }, w_{j_{\ell +1}}\} \in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
, as required. For the induction step, fix
$\{w_{j_\ell }, p_{j_{\ell }}\} = \{w_{j_\ell }, w_{j_{\ell +1}}\} \in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
, as required. For the induction step, fix
![]() $\ell '$
satisfying
$\ell '$
satisfying
![]() $\ell \leq \ell ' \lt k-1$
and assume Claim 3 for
$\ell \leq \ell ' \lt k-1$
and assume Claim 3 for
![]() $\ell '$
. Since Claim 3 implies
$\ell '$
. Since Claim 3 implies
![]() $w_{j_{\ell '}}\in \kappa$
and
$w_{j_{\ell '}}\in \kappa$
and
![]() $\{w_{j_{\ell '}}, w_{j_{\ell '+1}}\}\in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
,
$\{w_{j_{\ell '}}, w_{j_{\ell '+1}}\}\in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
,
![]() $w_{j_{\ell '}}$
and
$w_{j_{\ell '}}$
and
![]() $w_{j_{\ell '+1}}$
are in the same component of
$w_{j_{\ell '+1}}$
are in the same component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
, namely,
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
, namely,
![]() $\kappa$
. Then since
$\kappa$
. Then since
![]() $w_{j_{\ell '+1}}$
is in a giant component of
$w_{j_{\ell '+1}}$
is in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
but is not in a giant component of
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})]$
but is not in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash \{ w_{j_{\ell '+1}}, p_{j_{\ell '+1}}\}]$
, the edge
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash \{ w_{j_{\ell '+1}}, p_{j_{\ell '+1}}\}]$
, the edge
![]() $\{w_{j_{\ell '+1}}, p_{j_{\ell '+1}}\} = \{w_{j_{\ell '+1}}, w_{j_{\ell '+2}}\} \in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
, as required.
$\{w_{j_{\ell '+1}}, p_{j_{\ell '+1}}\} = \{w_{j_{\ell '+1}}, w_{j_{\ell '+2}}\} \in{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})$
, as required.
Claim 3 implies that for every
![]() $j$
satisfying
$j$
satisfying
![]() $j_\ell \leq j \leq k$
,
$j_\ell \leq j \leq k$
,
![]() $w_j\in V(\kappa )$
. Let
$w_j\in V(\kappa )$
. Let
![]() $e = \{w_k,p_k\}$
. Since
$e = \{w_k,p_k\}$
. Since
![]() $w_k$
is not in a giant component of
$w_k$
is not in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{e\}]$
and the edge
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{e\}]$
and the edge
![]() $e$
is not on the path
$e$
is not on the path
![]() $w_{j_\ell },\ldots, w_k$
it follows that no vertices in
$w_{j_\ell },\ldots, w_k$
it follows that no vertices in
![]() $W'$
are in a giant component of
$W'$
are in a giant component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{e\}]$
. We now consider two cases.
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{e\}]$
. We now consider two cases.
Case 3a.
![]() $k - \ell \geq r'/2$
.
$k - \ell \geq r'/2$
.
Take
![]() $S = \{e\}$
. Suppose that
$S = \{e\}$
. Suppose that
![]() $|V|$
is sufficiently large that
$|V|$
is sufficiently large that
![]() $|S| \lt 9\Delta |V|/200$
. For any
$|S| \lt 9\Delta |V|/200$
. For any
![]() $j\in J'$
let
$j\in J'$
let
![]() $\kappa _j$
be the component containing
$\kappa _j$
be the component containing
![]() $w_j$
in
$w_j$
in
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j,p_j\}]$
. Item 2 of Lemma29 implies that all but at most
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\setminus \{w_j,p_j\}]$
. Item 2 of Lemma29 implies that all but at most
![]() $45\Delta$
vertices of
$45\Delta$
vertices of
![]() $\kappa _j$
are such that all their incident edges belong to a polymer of
$\kappa _j$
are such that all their incident edges belong to a polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
. Item 3 implies that there are at most
${\mathcal{F}}^{\mathrm{ord}}$
. Item 3 implies that there are at most
![]() $50 \Delta ^2$
polymers containing vertices of
$50 \Delta ^2$
polymers containing vertices of
![]() $\kappa _j$
. Since
$\kappa _j$
. Since
![]() $k-\ell \geq r'/2$
, we conclude that there are at least
$k-\ell \geq r'/2$
, we conclude that there are at least
![]() $ r'/2 - 45\Delta$
vertices of
$ r'/2 - 45\Delta$
vertices of
![]() $W'\cap V(\kappa )$
such that all their incident edges are in a polymer, and at most
$W'\cap V(\kappa )$
such that all their incident edges are in a polymer, and at most
![]() $50\Delta ^2$
polymers containing them. Hence there a polymer of size at least
$50\Delta ^2$
polymers containing them. Hence there a polymer of size at least
![]() $\frac{\Delta }{2} \times \frac{r'/2 - 45\Delta }{50\Delta ^2}\geq \frac{r' - 90\Delta }{200\Delta } \geq \frac{r}{400\Delta (1+K)}-1$
.
$\frac{\Delta }{2} \times \frac{r'/2 - 45\Delta }{50\Delta ^2}\geq \frac{r' - 90\Delta }{200\Delta } \geq \frac{r}{400\Delta (1+K)}-1$
.
Case 3b.
![]() $k - \ell \lt r'/2$
.
$k - \ell \lt r'/2$
.
We have already seen that
![]() $w_{r'},\ldots, w_{\ell -1}$
is a path in
$w_{r'},\ldots, w_{\ell -1}$
is a path in
![]() $G$
with length at least
$G$
with length at least
![]() $\ell - r' \geq r'/2$
and its vertices are not in
$\ell - r' \geq r'/2$
and its vertices are not in
![]() $V(\kappa )$
. By Item 1 of Lemma29, every edge incident to one of these vertices is contained in a polymer of
$V(\kappa )$
. By Item 1 of Lemma29, every edge incident to one of these vertices is contained in a polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
. Since the vertices form a path in
${\mathcal{F}}^{\mathrm{ord}}$
. Since the vertices form a path in
![]() $G$
, the edges adjacent to them are all in the same polymer of
$G$
, the edges adjacent to them are all in the same polymer of
![]() ${\mathcal{F}}^{\mathrm{ord}}$
. Thus,
${\mathcal{F}}^{\mathrm{ord}}$
. Thus,
![]() ${\mathcal{F}}^{\mathrm{ord}}$
has a polymer of size at least
${\mathcal{F}}^{\mathrm{ord}}$
has a polymer of size at least
![]() $(r'/2) \geq \frac{(k/2)-1}{2} \geq \frac{r}{4(K+1)}-1$
.
$(r'/2) \geq \frac{(k/2)-1}{2} \geq \frac{r}{4(K+1)}-1$
.
Next we will show that the termination condition from Step 1 of the process is unlikely to happen.
Lemma 45.
Let
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K\geq 0$
be integers. Let
$K\geq 0$
be integers. Let
![]() $\delta \in (0,1/2)$
be a real number. Let
$\delta \in (0,1/2)$
be a real number. Let
![]() $\eta = \min \{\delta /5,1/100\}$
There are positive real numbers
$\eta = \min \{\delta /5,1/100\}$
There are positive real numbers
![]() $q_0\geq 1$
and
$q_0\geq 1$
and
![]() $n_0$
such that the following holds for all
$n_0$
such that the following holds for all
![]() $q\geq q_0$
and all
$q\geq q_0$
and all
![]() $\beta \geq \beta _c$
. Let
$\beta \geq \beta _c$
. Let
![]() $G=(V,E)$
. Let
$G=(V,E)$
. Let
![]() $n=|V|$
and let
$n=|V|$
and let
![]() $v$
be a vertex in
$v$
be a vertex in
![]() $V$
. Let
$V$
. Let
![]() $r$
be a real number satisfying
$r$
be a real number satisfying
![]() $r \leq \tfrac{1}{3}\log _{\Delta -1}(n)$
. Then
$r \leq \tfrac{1}{3}\log _{\Delta -1}(n)$
. Then
![]() $\pi _G^{\mathrm{ord}}(|{\mathrm{In}}({\mathcal{F}})\backslash E(B_r(v))| \lt (1-\eta )|E|) = e^{-\Omega (n)}$
.
$\pi _G^{\mathrm{ord}}(|{\mathrm{In}}({\mathcal{F}})\backslash E(B_r(v))| \lt (1-\eta )|E|) = e^{-\Omega (n)}$
.
Proof. Let
![]() $r_0(n) = \tfrac{1}{3} \log _{\Delta -1}(n)$
so
$r_0(n) = \tfrac{1}{3} \log _{\Delta -1}(n)$
so
![]() $r(n) \leq r_0(n)$
. Let
$r(n) \leq r_0(n)$
. Let
![]() $n_0$
be sufficiently large that
$n_0$
be sufficiently large that
![]() $\Delta ^{r(n_0)+1} \leq (\eta - \zeta ) n_0\Delta /2$
, where
$\Delta ^{r(n_0)+1} \leq (\eta - \zeta ) n_0\Delta /2$
, where
![]() $\zeta$
is the constant from Lemma3. By Lemma3,
$\zeta$
is the constant from Lemma3. By Lemma3,
However, if
![]() $|{\mathrm{In}}({\mathcal{F}})| \gt (1-\zeta )|E|$
, then
$|{\mathrm{In}}({\mathcal{F}})| \gt (1-\zeta )|E|$
, then
5.3 Proof of WSM within the ordered phase
We can now prove Theorem5. We start with the following Lemma.
Lemma 46.
Let
![]() $\Delta \geq 5$
and
$\Delta \geq 5$
and
![]() $K\geq 0$
be integers and let
$K\geq 0$
be integers and let
![]() $\delta \in (0, 1/2)$
be a real. There is
$\delta \in (0, 1/2)$
be a real. There is
![]() $M=M(\Delta, K)\gt 0$
such that the following holds for all sufficiently large
$M=M(\Delta, K)\gt 0$
such that the following holds for all sufficiently large
![]() $q$
and any
$q$
and any
![]() $\beta \geq \beta _c$
. For all sufficiently large
$\beta \geq \beta _c$
. For all sufficiently large
![]() $n$
and any
$n$
and any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G\in{\mathcal{G}}_{\Delta, \delta, K}$
, the RC model on
$G\in{\mathcal{G}}_{\Delta, \delta, K}$
, the RC model on
![]() $G$
with parameters
$G$
with parameters
![]() $q$
and
$q$
and
![]() $\beta$
has WSM within the ordered phase at radius
$\beta$
has WSM within the ordered phase at radius
![]() $r_1$
satisfying
$r_1$
satisfying
![]() $r_1\leq \frac{{M}}{\beta }\log _{\Delta -1} (n)$
.
$r_1\leq \frac{{M}}{\beta }\log _{\Delta -1} (n)$
.
Proof. Recall that
![]() $\eta = \min \{\delta /5,1/100\}$
. Let
$\eta = \min \{\delta /5,1/100\}$
. Let
![]() $M = 2000 \times 400 \times (2+K) \Delta \log (\Delta -1)$
.
$M = 2000 \times 400 \times (2+K) \Delta \log (\Delta -1)$
.
Let
![]() $r(n,\beta ) \;:\!=\; \frac{{M}}{\beta }\log _{\Delta -1}(n)$
. Let
$r(n,\beta ) \;:\!=\; \frac{{M}}{\beta }\log _{\Delta -1}(n)$
. Let
![]() $\beta _0(q) \;:\!=\; \log (q^{1.9/\Delta }+1)$
. Let
$\beta _0(q) \;:\!=\; \log (q^{1.9/\Delta }+1)$
. Let
![]() $q_0$
and
$q_0$
and
![]() $n_0$
be large enough that
$n_0$
be large enough that
-
•
 $\beta _c(q_0) \geq \beta _0(q_0)$
.
$\beta _c(q_0) \geq \beta _0(q_0)$
. -
•
 $\beta _0(q_0) \geq 3 M$
.
$\beta _0(q_0) \geq 3 M$
. -
•
 $2 n_0^{-3/2} + f(n_0) \leq 1/(50 \Delta n_0)$
where
$2 n_0^{-3/2} + f(n_0) \leq 1/(50 \Delta n_0)$
where
 $f(n)$
is the
$f(n)$
is the
 $e^{-\Omega (n)}$
upper bound from Lemma45.
$e^{-\Omega (n)}$
upper bound from Lemma45.
For every
![]() $\beta$
define
$\beta$
define
![]() $n_1(\beta )$
to be the smallest positive integer such that
$n_1(\beta )$
to be the smallest positive integer such that
-
•
 $\frac{r(n_1(\beta ),\beta )}{400\Delta (1+K)}-1 \geq \frac{r(n_1(\beta ),\beta )}{400\Delta (2+K)}$
$\frac{r(n_1(\beta ),\beta )}{400\Delta (1+K)}-1 \geq \frac{r(n_1(\beta ),\beta )}{400\Delta (2+K)}$
Now fix
![]() $q\geq q_0$
and
$q\geq q_0$
and
![]() $\beta \geq \beta _c(q)$
.
$\beta \geq \beta _c(q)$
.
Consider any
![]() $n\geq \max \{n_0,n_1(\beta )\}$
. Consider an
$n\geq \max \{n_0,n_1(\beta )\}$
. Consider an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G\in{\mathcal{G}}_{\Delta, \delta, K}$
. Let
$G\in{\mathcal{G}}_{\Delta, \delta, K}$
. Let
![]() $r_1$
be as in Lemma44. Use the process to generate
$r_1$
be as in Lemma44. Use the process to generate
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
. We wish to show that for every edge
${\mathcal{F}}^+$
. We wish to show that for every edge
![]() $e$
incident to
$e$
incident to
![]() $v$
,
$v$
,
By Observation41
![]() ${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}} \sim \pi ^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}_{r+1}^+(v)}$
. By Lemma44, if
${\mathcal{F}}^+\sim \pi _{{\mathcal{B}}_{r+1}^+(v)}$
. By Lemma44, if
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
do not agree on an edge incident to
${\mathcal{F}}^+$
do not agree on an edge incident to
![]() $v$
, then
$v$
, then
![]() ${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
![]() $\frac{r(n,\beta )}{400\Delta (1+K)}-1$
, or
$\frac{r(n,\beta )}{400\Delta (1+K)}-1$
, or
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash E(B_{r_1}(v))| \lt (1-\eta )|E|$
. Thus the probability that
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{ord}})\backslash E(B_{r_1}(v))| \lt (1-\eta )|E|$
. Thus the probability that
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
do not agree on an edge incident to
${\mathcal{F}}^+$
do not agree on an edge incident to
![]() $v$
is at most the sum of probabilities of those two events.
$v$
is at most the sum of probabilities of those two events.
Applying Lemma28, noting that
![]() $\frac{r(n,\beta )}{400\Delta (1+K)}-1 \geq \frac{r(n,\beta )}{400\Delta (2+K)}$
and (given the lower bound on
$\frac{r(n,\beta )}{400\Delta (1+K)}-1 \geq \frac{r(n,\beta )}{400\Delta (2+K)}$
and (given the lower bound on
![]() $M$
at the start of the proof) that this quantity is at least
$M$
at the start of the proof) that this quantity is at least
![]() $2000\log n/\beta$
, the probability of the first event is at most
$2000\log n/\beta$
, the probability of the first event is at most
![]() $2n^{-3/2}$
.
$2n^{-3/2}$
.
Note that
![]() $r(n,\beta ) \leq \tfrac 13 \log _{\Delta -1}(n)$
. Applying Lemma45, the probability of the second event is
$r(n,\beta ) \leq \tfrac 13 \log _{\Delta -1}(n)$
. Applying Lemma45, the probability of the second event is
![]() $f(n) = e^{-\Omega (n)}$
. The result follows by summing these probabilities.
$f(n) = e^{-\Omega (n)}$
. The result follows by summing these probabilities.
Finally, we use Lemma46 to prove Theorem5.
Proof. By Lemmas7 and 16, there exist
![]() $K=K(\Delta )\gt 0$
and
$K=K(\Delta )\gt 0$
and
![]() $\delta =\delta (\Delta ) \in (0,1/2)$
such that, w.h.p.,
$\delta =\delta (\Delta ) \in (0,1/2)$
such that, w.h.p.,
![]() $G\sim{\mathcal{G}}_{\Delta, n}$
is in
$G\sim{\mathcal{G}}_{\Delta, n}$
is in
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
. Let
${\mathcal{G}}_{\Delta, \delta, K}$
. Let
![]() $M = M(\Delta, K)$
be as in Lemma46, and note that
$M = M(\Delta, K)$
be as in Lemma46, and note that
![]() $M$
is in fact only dependent on
$M$
is in fact only dependent on
![]() $\Delta$
. By Lemma46, for all
$\Delta$
. By Lemma46, for all
![]() $q$
sufficiently large and
$q$
sufficiently large and
![]() $\beta \geq \beta _c$
, for all
$\beta \geq \beta _c$
, for all
![]() $n$
sufficiently large and any
$n$
sufficiently large and any
![]() $n$
-vertex
$n$
-vertex
![]() $G\in{\mathcal{G}}_{\Delta, \delta, K}$
,
$G\in{\mathcal{G}}_{\Delta, \delta, K}$
,
![]() $G$
has a WSM within the ordered phase at radius
$G$
has a WSM within the ordered phase at radius
![]() $r_1$
where
$r_1$
where
![]() $r_1 \leq \tfrac{M}\beta \log _{\Delta -1}(n)$
.
$r_1 \leq \tfrac{M}\beta \log _{\Delta -1}(n)$
.
6. Proof of WSM within the disordered phase
We will prove that for
![]() $q$
large enough, all large enough graphs in
$q$
large enough, all large enough graphs in
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
have WSM within the disordered phase on all low enough temperatures. We use the same notion of partial configurations as in Section 5.1.
${\mathcal{G}}_{\Delta, \delta, K}$
have WSM within the disordered phase on all low enough temperatures. We use the same notion of partial configurations as in Section 5.1.
Definition 47.
Let
![]() $\mathcal{A}$
be a partial configuration in
$\mathcal{A}$
be a partial configuration in
![]() $\Omega ^*$
. If
$\Omega ^*$
. If
![]() $\Omega _{\mathcal{A}} \cap \Omega ^{\mathrm{dis}}$
is non-empty, then
$\Omega _{\mathcal{A}} \cap \Omega ^{\mathrm{dis}}$
is non-empty, then
![]() $\pi ^{\mathrm{dis}}_{\mathcal{A}}$
is the conditional distribution of
$\pi ^{\mathrm{dis}}_{\mathcal{A}}$
is the conditional distribution of
![]() $\pi ^{\mathrm{dis}}$
in
$\pi ^{\mathrm{dis}}$
in
![]() $\Omega _{\mathcal{A}}\cap \Omega ^{\mathrm{dis}}$
.
$\Omega _{\mathcal{A}}\cap \Omega ^{\mathrm{dis}}$
.
For a set
![]() $F\subseteq E$
, define the distribution
$F\subseteq E$
, define the distribution
![]() $\pi ^{\mathrm{dis}}_F$
to be the distribution on
$\pi ^{\mathrm{dis}}_F$
to be the distribution on
![]() $\Omega _F$
, such that for
$\Omega _F$
, such that for
![]() ${\mathcal{A}}\in \Omega _F$
,
${\mathcal{A}}\in \Omega _F$
,
![]() $\pi _F^{\mathrm{dis}}({\mathcal{A}}) = \pi ^{\mathrm{dis}}(\Omega _{\mathcal{A}})$
.
$\pi _F^{\mathrm{dis}}({\mathcal{A}}) = \pi ^{\mathrm{dis}}(\Omega _{\mathcal{A}})$
.
First we prove the following lemma showing that a suitable coupling exists.
Lemma 48.
Fix
![]() $\Delta \geq 5$
,
$\Delta \geq 5$
,
![]() $K\geq 0$
integers, and
$K\geq 0$
integers, and
![]() $\delta \in (0, 1/2)$
a real. Then, for all
$\delta \in (0, 1/2)$
a real. Then, for all
![]() $q$
large enough and
$q$
large enough and
![]() $\beta \leq \log (q^{2.1/\Delta }+1)$
, the following holds for all
$\beta \leq \log (q^{2.1/\Delta }+1)$
, the following holds for all
![]() $G=(V,E)\in{\mathcal{G}}_{\Delta, \delta, K}$
with sufficiently many vertices. Let
$G=(V,E)\in{\mathcal{G}}_{\Delta, \delta, K}$
with sufficiently many vertices. Let
![]() $v\in V$
and
$v\in V$
and
![]() $r \;:\!=\; \frac{1}{3}\log _{\Delta -1} |V|$
. Then there is an integer
$r \;:\!=\; \frac{1}{3}\log _{\Delta -1} |V|$
. Then there is an integer
![]() $r_1$
satisfying
$r_1$
satisfying
![]() $r \geq r_1 \geq \frac{r}{K+1}-1$
and there is a coupling
$r \geq r_1 \geq \frac{r}{K+1}-1$
and there is a coupling
![]() $({\mathcal{F}}^-,{\mathcal{F}}^{\mathrm{dis}})$
such that
$({\mathcal{F}}^-,{\mathcal{F}}^{\mathrm{dis}})$
such that
![]() ${\mathcal{F}}^-\sim \pi _{{\mathcal{B}}^-_{r_1}(v)}$
and
${\mathcal{F}}^-\sim \pi _{{\mathcal{B}}^-_{r_1}(v)}$
and
![]() ${\mathcal{F}}^{\mathrm{dis}}\sim \pi ^{\mathrm{dis}}$
, and moreover at least one of the following holds:
${\mathcal{F}}^{\mathrm{dis}}\sim \pi ^{\mathrm{dis}}$
, and moreover at least one of the following holds:
-
1.
 $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}\backslash E(B_{r_1}(v))| \gt \eta |E| - |E(B_{r_1}(v))|$
.
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}\backslash E(B_{r_1}(v))| \gt \eta |E| - |E(B_{r_1}(v))|$
. -
2. For any edge
 $e$
incident to
$e$
incident to
 $v$
,
$v$
,
 ${\mathcal{F}}^-(e) ={\mathcal{F}}^{\mathrm{dis}}(e)$
.
${\mathcal{F}}^-(e) ={\mathcal{F}}^{\mathrm{dis}}(e)$
. -
3.
 $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})]$
has a component with at least
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})]$
has a component with at least
 $\frac{r}{K+1}-2$
edges.
$\frac{r}{K+1}-2$
edges.
Proof. We use the definition of
![]() $T_0$
and
$T_0$
and
![]() $\mathcal{E}$
from Definition31. By Observation33, we get
$\mathcal{E}$
from Definition31. By Observation33, we get
![]() $r_1$
and
$r_1$
and
![]() $r_2$
satisfying
$r_2$
satisfying
![]() $r\geq r_1 \gt r_2 \geq 0$
such that
$r\geq r_1 \gt r_2 \geq 0$
such that
![]() $r_1-r_2\geq \frac{r}{K+1}-1$
and
$r_1-r_2\geq \frac{r}{K+1}-1$
and
![]() $E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
contains no edges from
$E(B_{r_1}(v))\setminus E(B_{r_2}(v))$
contains no edges from
![]() $\mathcal{E}$
. Let
$\mathcal{E}$
. Let
![]() $T$
be the tree consisting of the first
$T$
be the tree consisting of the first
![]() $r_1 + 1$
levels of
$r_1 + 1$
levels of
![]() $T_0$
, that is,
$T_0$
, that is,
![]() $T_0[B_{r_1}(v)]$
.
$T_0[B_{r_1}(v)]$
.
Construct the coupling as follows: First, let
![]() $F_0\;:\!=\; E\setminus E(B_{r_1}(v))$
and
$F_0\;:\!=\; E\setminus E(B_{r_1}(v))$
and
![]() ${\mathcal{F}}_0^{\mathrm{dis}}\sim \pi _{F_0}^{\mathrm{dis}}$
. If
${\mathcal{F}}_0^{\mathrm{dis}}\sim \pi _{F_0}^{\mathrm{dis}}$
. If
![]() $|{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})| \gt \eta |E| - |E(B_{r_1}(v))|$
, then let
$|{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})| \gt \eta |E| - |E(B_{r_1}(v))|$
, then let
![]() ${\mathcal{F}}^{\mathrm{dis}}\sim \pi ^{\mathrm{dis}}_{{\mathcal{F}}_0^{\mathrm{dis}}}$
and
${\mathcal{F}}^{\mathrm{dis}}\sim \pi ^{\mathrm{dis}}_{{\mathcal{F}}_0^{\mathrm{dis}}}$
and
![]() ${\mathcal{F}}^-\sim \pi ^{\mathrm{dis}}_{{\mathcal{B}}_{r_1}^-(v)}$
. Otherwise, let
${\mathcal{F}}^-\sim \pi ^{\mathrm{dis}}_{{\mathcal{B}}_{r_1}^-(v)}$
. Otherwise, let
![]() ${\mathcal{F}}_0^-$
be the partial configuration with
${\mathcal{F}}_0^-$
be the partial configuration with
![]() $R({\mathcal{F}}_0^-) = \mathrm{Out}({\mathcal{F}}_0^-) = F_0$
, let
$R({\mathcal{F}}_0^-) = \mathrm{Out}({\mathcal{F}}_0^-) = F_0$
, let
![]() $F_1 = E\setminus E(B_{r_2+1}(v))$
and generate, optimally coupled,
$F_1 = E\setminus E(B_{r_2+1}(v))$
and generate, optimally coupled,
![]() ${\mathcal{F}}_1^{\mathrm{dis}}\sim \pi _{{\mathcal{F}}_0^{\mathrm{dis}},F_1}$
and
${\mathcal{F}}_1^{\mathrm{dis}}\sim \pi _{{\mathcal{F}}_0^{\mathrm{dis}},F_1}$
and
![]() ${\mathcal{F}}_1^-\sim \pi _{{\mathcal{F}}_0^-,F_1}$
. Finally, generate, optimally coupled
${\mathcal{F}}_1^-\sim \pi _{{\mathcal{F}}_0^-,F_1}$
. Finally, generate, optimally coupled
![]() ${\mathcal{F}}^-\sim \pi _{{\mathcal{F}}^-_1}$
and
${\mathcal{F}}^-\sim \pi _{{\mathcal{F}}^-_1}$
and
![]() ${\mathcal{F}}^{\mathrm{dis}}\sim \pi _{{\mathcal{F}}^{\mathrm{dis}}_1}$
.
${\mathcal{F}}^{\mathrm{dis}}\sim \pi _{{\mathcal{F}}^{\mathrm{dis}}_1}$
.
First note, that
![]() ${\mathcal{F}}^{\mathrm{dis}}\sim \pi ^{\mathrm{dis}}$
and
${\mathcal{F}}^{\mathrm{dis}}\sim \pi ^{\mathrm{dis}}$
and
![]() ${\mathcal{F}}^-\sim \pi _{{\mathcal{B}}_{r_1}^-(v)}$
. In the case
${\mathcal{F}}^-\sim \pi _{{\mathcal{B}}_{r_1}^-(v)}$
. In the case
![]() $|{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})| \gt \eta |E| - |E(B_{r_1}(v))|$
it follows by construction. Otherwise, we may note that any refinement of
$|{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})| \gt \eta |E| - |E(B_{r_1}(v))|$
it follows by construction. Otherwise, we may note that any refinement of
![]() ${\mathcal{F}}^{\mathrm{dis}}_0$
has at most
${\mathcal{F}}^{\mathrm{dis}}_0$
has at most
![]() $\eta |E|$
edges, as
$\eta |E|$
edges, as
![]() $|E\setminus R({\mathcal{F}}_0^{\mathrm{dis}})| = |E(B_{r_1}(v))|$
, thus
$|E\setminus R({\mathcal{F}}_0^{\mathrm{dis}})| = |E(B_{r_1}(v))|$
, thus
![]() $\pi _{{\mathcal{F}}_0^{\mathrm{dis}},F_1} = \pi _{{\mathcal{F}}_0^{\mathrm{dis}},F_1}^{\mathrm{dis}}$
. Similarly,
$\pi _{{\mathcal{F}}_0^{\mathrm{dis}},F_1} = \pi _{{\mathcal{F}}_0^{\mathrm{dis}},F_1}^{\mathrm{dis}}$
. Similarly,
![]() $\pi _{{\mathcal{F}}^{\mathrm{dis}}_1} = \pi _{{\mathcal{F}}_1^{\mathrm{dis}}}^{\mathrm{dis}}$
. For
$\pi _{{\mathcal{F}}^{\mathrm{dis}}_1} = \pi _{{\mathcal{F}}_1^{\mathrm{dis}}}^{\mathrm{dis}}$
. For
![]() ${\mathcal{F}}^-$
the result follows from the fact that a configuration
${\mathcal{F}}^-$
the result follows from the fact that a configuration
![]() $\mathcal{F}$
is a refinement of
$\mathcal{F}$
is a refinement of
![]() ${\mathcal{F}}_0^-$
if and only if
${\mathcal{F}}_0^-$
if and only if
![]() $\pi _{{\mathcal{B}}^-_{r_1}(v)}({\mathcal{F}})\gt 0$
.
$\pi _{{\mathcal{B}}^-_{r_1}(v)}({\mathcal{F}})\gt 0$
.
Now we proceed to show that the resulting configurations satisfy one of the conditions. We have three exhaustive cases, and we show that each corresponds to one of the conditions.
Case 1.
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \gt \eta |E| - |E(B_{r_1}(v))|$
.
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \gt \eta |E| - |E(B_{r_1}(v))|$
.
Then its refinement
![]() ${\mathcal{F}}^{\mathrm{dis}}$
satisfies
${\mathcal{F}}^{\mathrm{dis}}$
satisfies
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})\backslash E(B_{r_1}(v))| \gt \eta |E| - |E(B_{r_1}(v))|$
, since
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})\backslash E(B_{r_1}(v))| \gt \eta |E| - |E(B_{r_1}(v))|$
, since
![]() $E(B_{r_1}(v))\cap R({\mathcal{F}}^{\mathrm{dis}}_0) = \emptyset$
, thus the first condition holds.
$E(B_{r_1}(v))\cap R({\mathcal{F}}^{\mathrm{dis}}_0) = \emptyset$
, thus the first condition holds.
Case 2.
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \leq \eta |E| - |E(B_{r_1}(v))|$
, and
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \leq \eta |E| - |E(B_{r_1}(v))|$
, and
![]() $\xi ({\mathcal{F}}_1^{\mathrm{dis}})$
is a free boundary. That is, no two vertices in
$\xi ({\mathcal{F}}_1^{\mathrm{dis}})$
is a free boundary. That is, no two vertices in
![]() $\partial (F_1)$
are in the same component of
$\partial (F_1)$
are in the same component of
![]() $G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
.
Since
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \leq \eta |E| - |E(B_{r_1}(v))|$
, we have
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \leq \eta |E| - |E(B_{r_1}(v))|$
, we have
![]() $R({\mathcal{F}}_0^{\mathrm{dis}}) = R({\mathcal{F}}_0^-) = F_0$
, and
$R({\mathcal{F}}_0^{\mathrm{dis}}) = R({\mathcal{F}}_0^-) = F_0$
, and
![]() $R({\mathcal{F}}_1^{\mathrm{dis}}) = R({\mathcal{F}}_1^0) = F_1$
. Also,
$R({\mathcal{F}}_1^{\mathrm{dis}}) = R({\mathcal{F}}_1^0) = F_1$
. Also,
![]() $\emptyset ={\mathrm{In}}({\mathcal{F}}_0^-)\subseteq{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})$
, thus by Corollary53, and by the fact that
$\emptyset ={\mathrm{In}}({\mathcal{F}}_0^-)\subseteq{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})$
, thus by Corollary53, and by the fact that
![]() ${\mathcal{F}}_1^{\mathrm{dis}}$
and
${\mathcal{F}}_1^{\mathrm{dis}}$
and
![]() ${\mathcal{F}}_1^-$
were optimally coupled, also
${\mathcal{F}}_1^-$
were optimally coupled, also
![]() ${\mathrm{In}}({\mathcal{F}}_1^-)\subseteq{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})$
. So since no two vertices in
${\mathrm{In}}({\mathcal{F}}_1^-)\subseteq{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})$
. So since no two vertices in
![]() $\partial (R({\mathcal{F}}_1^{\mathrm{dis}})) = \partial (F_1) = \partial (R({\mathcal{F}}_1^-))$
are in the same component of
$\partial (R({\mathcal{F}}_1^{\mathrm{dis}})) = \partial (F_1) = \partial (R({\mathcal{F}}_1^-))$
are in the same component of
![]() $G[{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})]$
, it is also true that no two vertices in
$G[{\mathrm{In}}({\mathcal{F}}_0^{\mathrm{dis}})]$
, it is also true that no two vertices in
![]() $\partial (F_1)$
are in the same component of
$\partial (F_1)$
are in the same component of
![]() $G[{\mathrm{In}}({\mathcal{F}}_0^-)]$
. So
$G[{\mathrm{In}}({\mathcal{F}}_0^-)]$
. So
![]() $\xi ({\mathcal{F}}^{\mathrm{dis}}_0) = \xi ({\mathcal{F}}^-_0)$
, thus by Observation51 and by the fact that they were optimally coupled,
$\xi ({\mathcal{F}}^{\mathrm{dis}}_0) = \xi ({\mathcal{F}}^-_0)$
, thus by Observation51 and by the fact that they were optimally coupled,
![]() ${\mathcal{F}}^-$
and
${\mathcal{F}}^-$
and
![]() ${\mathcal{F}}^{\mathrm{dis}}$
agree on the edges of
${\mathcal{F}}^{\mathrm{dis}}$
agree on the edges of
![]() $E\setminus F_1 = E(B_{r_2+1}(v))$
. Note that since
$E\setminus F_1 = E(B_{r_2+1}(v))$
. Note that since
![]() $r_2 + 1 \geq 1$
, all edges incident to
$r_2 + 1 \geq 1$
, all edges incident to
![]() $v$
are in
$v$
are in
![]() $E(B_{r_2+1}(v))$
, thus
$E(B_{r_2+1}(v))$
, thus
![]() ${\mathcal{F}}^{\mathrm{dis}}$
and
${\mathcal{F}}^{\mathrm{dis}}$
and
![]() ${\mathcal{F}}^-$
agree on them. This corresponds to condition two.
${\mathcal{F}}^-$
agree on them. This corresponds to condition two.
Case 3.
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \leq \eta |E| - |E(B_{r_1}(v))|$
and there are distinct vertices
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}}_0)| \leq \eta |E| - |E(B_{r_1}(v))|$
and there are distinct vertices
![]() $u_1, u_2\in \partial (F_1)$
such that
$u_1, u_2\in \partial (F_1)$
such that
![]() $u_1$
and
$u_1$
and
![]() $u_2$
are in the same component of
$u_2$
are in the same component of
![]() $G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
.
Consider any path
![]() $\gamma$
between
$\gamma$
between
![]() $u_1$
and
$u_1$
and
![]() $u_2$
in the
$u_2$
in the
![]() $G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
. Since no edges in
$G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
. Since no edges in
![]() $B_{r_2}(v)$
are revealed in
$B_{r_2}(v)$
are revealed in
![]() ${\mathcal{F}}_1^{\mathrm{dis}}$
,
${\mathcal{F}}_1^{\mathrm{dis}}$
,
![]() $\gamma$
is contained in
$\gamma$
is contained in
![]() $E\setminus E(B_{r_2}(v))$
. Note that since
$E\setminus E(B_{r_2}(v))$
. Note that since
![]() $T_{u_1}$
and
$T_{u_1}$
and
![]() $T_{u_2}$
- the subtrees of
$T_{u_2}$
- the subtrees of
![]() $T$
rooted in
$T$
rooted in
![]() $u_1$
and
$u_1$
and
![]() $u_2$
, respectively, are disjoint,
$u_2$
, respectively, are disjoint,
![]() $V(\gamma )$
is not contained in
$V(\gamma )$
is not contained in
![]() $V(T_{u_1})$
. Let
$V(T_{u_1})$
. Let
![]() $e = \{w_1, w_2\}$
be the first edge on
$e = \{w_1, w_2\}$
be the first edge on
![]() $\gamma$
such that
$\gamma$
such that
![]() $w_1\in V(T_{u_1})$
and
$w_1\in V(T_{u_1})$
and
![]() $w_2\not \in V(T_{u_1})$
. Note that for any vertex
$w_2\not \in V(T_{u_1})$
. Note that for any vertex
![]() $w$
with
$w$
with
![]() $r_1 \gt d_G(w, v) \gt r_2$
, all edges incident to
$r_1 \gt d_G(w, v) \gt r_2$
, all edges incident to
![]() $w$
are edges of
$w$
are edges of
![]() $T$
, and in particular, if it also holds that if
$T$
, and in particular, if it also holds that if
![]() $w$
is a non-leaf vertex in
$w$
is a non-leaf vertex in
![]() $V(T_{u_1})$
, all incident edges to
$V(T_{u_1})$
, all incident edges to
![]() $w$
are in
$w$
are in
![]() $E(T_{u_1})$
.
$E(T_{u_1})$
.
Then, by construction and the choice of
![]() $r_1$
and
$r_1$
and
![]() $ r_2$
,
$ r_2$
,
![]() $\partial (F_1) = \{u\in V \mid d_G(u, v) = r_2 + 1\}$
. Also no edges incident to vertices with distance at most
$\partial (F_1) = \{u\in V \mid d_G(u, v) = r_2 + 1\}$
. Also no edges incident to vertices with distance at most
![]() $r_2$
from
$r_2$
from
![]() $v$
were revealed, so it must be the case that
$v$
were revealed, so it must be the case that
![]() $d_G(w_1, v) = r_1$
.
$d_G(w_1, v) = r_1$
.
Hence there is a path containing at least
![]() $r_1 - (r_2 + 1) \geq \frac{r}{K+1} - 2$
edges in
$r_1 - (r_2 + 1) \geq \frac{r}{K+1} - 2$
edges in
![]() $G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
, and thus also in
$G[{\mathrm{In}}({\mathcal{F}}_1^{\mathrm{dis}})]$
, and thus also in
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})]$
. So there is a connected component of
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})]$
. So there is a connected component of
![]() $G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})]$
with size at least
$G[{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})]$
with size at least
![]() $\frac{r}{K + 1}-2$
, which corresponds to the third condition.
$\frac{r}{K + 1}-2$
, which corresponds to the third condition.
Next we prove Theorem6.
Theorem 6.
For all integer
![]() $\Delta \geq 5$
, for all
$\Delta \geq 5$
, for all
![]() $q$
sufficiently large and any
$q$
sufficiently large and any
![]() $\beta \leq \beta _c$
, w.h.p. over
$\beta \leq \beta _c$
, w.h.p. over
![]() $G\sim{\mathcal{G}}_{n,\Delta }$
,
$G\sim{\mathcal{G}}_{n,\Delta }$
,
![]() $G$
has WSM within the disordered phase at a radius
$G$
has WSM within the disordered phase at a radius
![]() $r$
which satisfies
$r$
which satisfies
![]() $r\leq \tfrac{1}{3}\log _{\Delta -1}n$
.
$r\leq \tfrac{1}{3}\log _{\Delta -1}n$
.
Proof. By Lemmas7 and 16, there exist
![]() $K=K(\Delta )\gt 0$
and
$K=K(\Delta )\gt 0$
and
![]() $\delta =\delta (\Delta ) \in (0,1/2)$
such that, w.h.p.,
$\delta =\delta (\Delta ) \in (0,1/2)$
such that, w.h.p.,
![]() $G\sim{\mathcal{G}}_{\Delta, n}$
is in
$G\sim{\mathcal{G}}_{\Delta, n}$
is in
![]() ${\mathcal{G}}_{\Delta, \delta, K}$
. Let
${\mathcal{G}}_{\Delta, \delta, K}$
. Let
![]() $\beta _1(q) \;:\!=\;\log (q^{2.1/\Delta }+1)$
. Let
$\beta _1(q) \;:\!=\;\log (q^{2.1/\Delta }+1)$
. Let
![]() $\zeta$
be the constant from Lemma3 and let
$\zeta$
be the constant from Lemma3 and let
![]() $C'$
be constant implicit in Equation 2 so that this equation guarantees
$C'$
be constant implicit in Equation 2 so that this equation guarantees
![]() $\pi _G^{\mathrm{dis}}\Big (|{\mathrm{In}}({\mathcal{F}})|\geq \zeta |E|\Big ) \leq e^{-C' n}$
.
$\pi _G^{\mathrm{dis}}\Big (|{\mathrm{In}}({\mathcal{F}})|\geq \zeta |E|\Big ) \leq e^{-C' n}$
.
Let
![]() $q_0$
and
$q_0$
and
![]() $n_0$
be large enough that
$n_0$
be large enough that
-
•
 $\beta _c(q_0) \leq \beta _1(q_0)$
.
$\beta _c(q_0) \leq \beta _1(q_0)$
. -
• Lemmas3 and 48 apply. Lemma26 applies with
 $C = \frac{1}{3(2+K)\log (\Delta -1)}$
.
$C = \frac{1}{3(2+K)\log (\Delta -1)}$
. -
•
 $(\eta - \zeta ) n_0 \geq \Delta n_0^{1/3}$
and
$(\eta - \zeta ) n_0 \geq \Delta n_0^{1/3}$
and
 $C'n_0 \geq \log (100\Delta n_0)$
and
$C'n_0 \geq \log (100\Delta n_0)$
and
 $n_0\geq (50\Delta )^2$
.
$n_0\geq (50\Delta )^2$
. -
•
 $\frac{\log _{\Delta -1} n_0}{3(K+1)}-2\geq \frac{\log _{\Delta -1} n_0}{3(K+2)}$
,
$\frac{\log _{\Delta -1} n_0}{3(K+1)}-2\geq \frac{\log _{\Delta -1} n_0}{3(K+2)}$
,
Now fix
![]() $q\geq q_0$
and
$q\geq q_0$
and
![]() $\beta \leq \beta _c(q)$
.
$\beta \leq \beta _c(q)$
.
Consider any
![]() $n\geq n_0$
. Consider an
$n\geq n_0$
. Consider an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G=(V,E)\in{\mathcal{G}}_{\Delta, \delta, K}$
. Let
$G=(V,E)\in{\mathcal{G}}_{\Delta, \delta, K}$
. Let
![]() $r\;:\!=\; \frac 13 \log _{\Delta -1}(n)$
. Fix
$r\;:\!=\; \frac 13 \log _{\Delta -1}(n)$
. Fix
![]() $v\in V$
. Let
$v\in V$
. Let
![]() $r_1$
be as in Lemma48. Use the process to generate
$r_1$
be as in Lemma48. Use the process to generate
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
. We wish to show that for every edge
${\mathcal{F}}^+$
. We wish to show that for every edge
![]() $e$
incident to
$e$
incident to
![]() $v$
,
$v$
,
By Lemma48, if
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
do not agree on all edges incident to
${\mathcal{F}}^+$
do not agree on all edges incident to
![]() $v$
, then
$v$
, then
![]() $|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})|\geq \eta |E| - |E(B_{r_1}(v))|$
or
$|{\mathrm{In}}({\mathcal{F}}^{\mathrm{dis}})|\geq \eta |E| - |E(B_{r_1}(v))|$
or
![]() ${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
${\mathcal{F}}^{\mathrm{ord}}$
contains a polymer of size at least
![]() $\frac{r}{K+1}-2\geq \frac{\log n}{3(K+2)\log (\Delta -1)} = C \log n$
. Thus the probability that
$\frac{r}{K+1}-2\geq \frac{\log n}{3(K+2)\log (\Delta -1)} = C \log n$
. Thus the probability that
![]() ${\mathcal{F}}^{\mathrm{ord}}$
and
${\mathcal{F}}^{\mathrm{ord}}$
and
![]() ${\mathcal{F}}^+$
do not agree on all edges incident to
${\mathcal{F}}^+$
do not agree on all edges incident to
![]() $v$
is at most the sum of the probabilities of these two events.
$v$
is at most the sum of the probabilities of these two events.
Since
![]() $(\eta - \zeta ) n \geq \Delta n^{1/3}$
,
$(\eta - \zeta ) n \geq \Delta n^{1/3}$
,
![]() $\zeta |E| \leq \eta |E| - |E(B_{r_1}(v))|$
, so Lemma3 guarantees that the probability of the first event is at most
$\zeta |E| \leq \eta |E| - |E(B_{r_1}(v))|$
, so Lemma3 guarantees that the probability of the first event is at most
![]() $e^{-C'n}\leq \frac{1}{100\Delta n} = \frac{1}{200|E|}$
.
$e^{-C'n}\leq \frac{1}{100\Delta n} = \frac{1}{200|E|}$
.
By Lemma26, the probability of the second event is at most
![]() $n^{-3/2} / 2\leq \frac{1}{100\Delta n} = \frac{1}{200|E|}$
. The result follows by summing these probabilities.
$n^{-3/2} / 2\leq \frac{1}{100\Delta n} = \frac{1}{200|E|}$
. The result follows by summing these probabilities.
7. Proof of Theorems12 and 13
In this section, we provide the last ingredients that were used in the proof of Theorem1 by showing the
![]() $O(n\log n)$
bounds in Theorems12 and 13. The overall argument is quite close to what was presented in Section 2.4 for the proof of Theorem11; the only extra argument required is a slightly more refined estimate from the distance to stationarity using log-Sobolev constants to save an
$O(n\log n)$
bounds in Theorems12 and 13. The overall argument is quite close to what was presented in Section 2.4 for the proof of Theorem11; the only extra argument required is a slightly more refined estimate from the distance to stationarity using log-Sobolev constants to save an
![]() $O(\log n)$
factor (a similar argument appears in [Reference Blanca and Gheissari4]). We present first the relevant tools in Sections 7.1 and 7.2, and then finish the proofs in Section 7.3.
$O(\log n)$
factor (a similar argument appears in [Reference Blanca and Gheissari4]). We present first the relevant tools in Sections 7.1 and 7.2, and then finish the proofs in Section 7.3.
7.1 The log-sobolev constant and mixing time inequality
Let
![]() $\mu$
be a distribution supported on a set
$\mu$
be a distribution supported on a set
![]() $\Omega$
. For a function
$\Omega$
. For a function
![]() $g:\Omega \rightarrow \mathbb{R}_{\geq 0}$
, let
$g:\Omega \rightarrow \mathbb{R}_{\geq 0}$
, let
with the convention
![]() $0\log 0\;:\!=\;0$
. Moreover, for a reversible Markov chain
$0\log 0\;:\!=\;0$
. Moreover, for a reversible Markov chain
![]() $(X_t)_{t\geq 0}$
on
$(X_t)_{t\geq 0}$
on
![]() $\Omega$
with transition matrix
$\Omega$
with transition matrix
![]() $P\in \mathbb{R}^{\Omega \times \Omega }_{\geq 0}$
, let
$P\in \mathbb{R}^{\Omega \times \Omega }_{\geq 0}$
, let
![]() $\mathcal{E}(g,g)\;:\!=\;\tfrac{1}{2}\sum _{\omega, \omega '}\mu (\omega )P(\omega, \omega ')(g(\omega )-g(\omega '))^2$
be the Dirichlet form for
$\mathcal{E}(g,g)\;:\!=\;\tfrac{1}{2}\sum _{\omega, \omega '}\mu (\omega )P(\omega, \omega ')(g(\omega )-g(\omega '))^2$
be the Dirichlet form for
![]() $P$
. The standard log-Sobolev constant of the chain is then defined as
$P$
. The standard log-Sobolev constant of the chain is then defined as
 \begin{equation*}\alpha (P)\;:\!=\;\min _{\substack {g:\Omega \rightarrow \mathbb {R}_{\geq 0};\\[5pt] \mathrm {Ent}_{\mu }[g]\neq 0}}\frac {\mathcal {E}(\sqrt {g},\sqrt {g})}{\mathrm {Ent}_\mu [g]}.\end{equation*}
\begin{equation*}\alpha (P)\;:\!=\;\min _{\substack {g:\Omega \rightarrow \mathbb {R}_{\geq 0};\\[5pt] \mathrm {Ent}_{\mu }[g]\neq 0}}\frac {\mathcal {E}(\sqrt {g},\sqrt {g})}{\mathrm {Ent}_\mu [g]}.\end{equation*}
The following well-known connection between the log-Sobolev constant and the distance from stationarity can be found, for example, in [Reference Blanca and Gheissari4, Fact 6.1]. Let
![]() $\mu _{\min }=\min _{\omega \in \Omega }. \mu (\omega )$
. Then, for any
$\mu _{\min }=\min _{\omega \in \Omega }. \mu (\omega )$
. Then, for any
![]() $\gamma \lt \alpha (P)$
, it holds that
$\gamma \lt \alpha (P)$
, it holds that
7.2 Log-sobolev constant for free/wired tree-like neighbourhoods
Here we briefly discuss how to bound the log-Sobolev for the wired RC dynamics for tree-like neighbourhoods for integer
![]() $q\gt 1$
(cf. Remark10) using the results from [Reference Blanca, Chen, Štefankovič and Vigoda2] on the tree.
$q\gt 1$
(cf. Remark10) using the results from [Reference Blanca, Chen, Štefankovič and Vigoda2] on the tree.
Lemma 49.
Let
![]() $q\geq 2$
and
$q\geq 2$
and
![]() $\Delta \geq 3$
be integers, and
$\Delta \geq 3$
be integers, and
![]() $K,\beta \gt 0$
be reals. There exists
$K,\beta \gt 0$
be reals. There exists
![]() $\tilde{C}\gt 0$
such that the following holds for every
$\tilde{C}\gt 0$
such that the following holds for every
![]() $\Delta$
-regular graph
$\Delta$
-regular graph
![]() $G=(V,E)$
and any integer
$G=(V,E)$
and any integer
![]() $r\geq 1$
.
$r\geq 1$
.
Suppose that
![]() $\rho \in V$
is such that
$\rho \in V$
is such that
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. Then, with
$K$
-treelike. Then, with
![]() $n=|B_r(\rho )|$
, the log-Sobolev constant for the wired RC dynamics on
$n=|B_r(\rho )|$
, the log-Sobolev constant for the wired RC dynamics on
![]() $B_r(\rho )$
is
$B_r(\rho )$
is
![]() $\geq \tilde{C}/n$
.
$\geq \tilde{C}/n$
.
Proof. Let
![]() $T=T_{\Delta }(\rho )$
denote the
$T=T_{\Delta }(\rho )$
denote the
![]() $\Delta$
-regular tree rooted at
$\Delta$
-regular tree rooted at
![]() $\rho$
. Then, for integer
$\rho$
. Then, for integer
![]() $q\geq 2$
and
$q\geq 2$
and
![]() $\beta \gt 0$
, it is shown in [Reference Blanca, Chen, Štefankovič and Vigoda2, Proof of Lemma 32] that there exists
$\beta \gt 0$
, it is shown in [Reference Blanca, Chen, Štefankovič and Vigoda2, Proof of Lemma 32] that there exists
![]() $C\gt 0$
such that the log-Sobolev constant for the wired RC dynamics on
$C\gt 0$
such that the log-Sobolev constant for the wired RC dynamics on
![]() $T[B_r(\rho )]$
is
$T[B_r(\rho )]$
is
![]() $\geq C/N$
where
$\geq C/N$
where
![]() $N=|B_r(\rho )|$
.
$N=|B_r(\rho )|$
.
To translate this into a lower bound on the log-Sobolev constant of
![]() $G[B_r(\rho )]$
(which is
$G[B_r(\rho )]$
(which is
![]() $K$
-treelike) as in the statement of the lemma, we can just use the argument in [Reference Gheissari and Sinclair15, Proof of Lemma 4.4]. There, they show, for the Ising model with all plus boundary condition, it via a graph decomposition argument that there exists a constant
$K$
-treelike) as in the statement of the lemma, we can just use the argument in [Reference Gheissari and Sinclair15, Proof of Lemma 4.4]. There, they show, for the Ising model with all plus boundary condition, it via a graph decomposition argument that there exists a constant
![]() $C'=C(q,\beta, K,\Delta )$
independent of
$C'=C(q,\beta, K,\Delta )$
independent of
![]() $r$
such that
$r$
such that
![]() $\alpha \big (P_{G[B_r(\rho )]}\big )\geq C\alpha \big (P_{T[B_r(\rho )]}\big )$
whenever
$\alpha \big (P_{G[B_r(\rho )]}\big )\geq C\alpha \big (P_{T[B_r(\rho )]}\big )$
whenever
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. The details of the graph decomposition do not depend on the Ising model, so the exact same strategy yields the analogue for the RC model.
$K$
-treelike. The details of the graph decomposition do not depend on the Ising model, so the exact same strategy yields the analogue for the RC model.
The analogous result for the free boundary is available from [Reference Blanca and Gheissari4] for all
![]() $q\geq 1$
, we state here the following more precise version of Lemma9.
$q\geq 1$
, we state here the following more precise version of Lemma9.
Lemma 50 ([Reference Blanca and Gheissari4, Lemma 6.5]). Let
![]() $\Delta \geq 3$
be an integer, and
$\Delta \geq 3$
be an integer, and
![]() $q,K\gt 1$
,
$q,K\gt 1$
,
![]() $\beta \gt 0$
be reals. There exists
$\beta \gt 0$
be reals. There exists
![]() $C\gt 0$
such that the following holds for any
$C\gt 0$
such that the following holds for any
![]() $\Delta$
-regular graph
$\Delta$
-regular graph
![]() $G$
and integer
$G$
and integer
![]() $r\geq 1$
.
$r\geq 1$
.
Suppose that
![]() $\rho \in V$
is such that
$\rho \in V$
is such that
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. Then, with
$K$
-treelike. Then, with
![]() $n=|B_r(\rho )|$
, the log-Sobolev constant for the free RC dynamics on
$n=|B_r(\rho )|$
, the log-Sobolev constant for the free RC dynamics on
![]() $B_r(\rho )$
is
$B_r(\rho )$
is
![]() $\geq C/n$
.
$\geq C/n$
.
7.3 Completing the proof of Theorems 12 and 13
Proof of Theorems
12 and 13. We first show Theorem12. Consider therefore
![]() $\Delta \geq 5$
, and let
$\Delta \geq 5$
, and let
![]() $q$
be sufficiently large so that both Lemma3 and Theorem6 apply, and suppose that
$q$
be sufficiently large so that both Lemma3 and Theorem6 apply, and suppose that
![]() $\beta \leq \beta _c$
.
$\beta \leq \beta _c$
.
Consider
![]() $G=(V,E)\sim{\mathcal{G}}_{n,\Delta }$
with
$G=(V,E)\sim{\mathcal{G}}_{n,\Delta }$
with
![]() $n=|V|$
and
$n=|V|$
and
![]() $m=|E|$
. By Lemma7, we can assume that
$m=|E|$
. By Lemma7, we can assume that
![]() $G$
is locally
$G$
is locally
![]() $K$
-treelike. By Lemma3,
$K$
-treelike. By Lemma3,
![]() $\pi _G^{\mathrm{dis}}\big (|{\mathrm{In}}({\mathcal{F}})|\geq \zeta |E|\big )=\mathrm{e}^{-\Omega (n)}$
. By Theorem6,
$\pi _G^{\mathrm{dis}}\big (|{\mathrm{In}}({\mathcal{F}})|\geq \zeta |E|\big )=\mathrm{e}^{-\Omega (n)}$
. By Theorem6,
![]() $G$
has WSM within the disordered phase at radius
$G$
has WSM within the disordered phase at radius
![]() $r$
for some
$r$
for some
![]() $r\leq \tfrac{1}{3}\log _{\Delta -1}n$
.
$r\leq \tfrac{1}{3}\log _{\Delta -1}n$
.
We will consider the RC dynamics
![]() $(X_t)_{t\geq 0}$
with
$(X_t)_{t\geq 0}$
with
![]() $X_0$
being the all-out configuration on the edges. We will also consider the ‘disordered’ RC dynamics
$X_0$
being the all-out configuration on the edges. We will also consider the ‘disordered’ RC dynamics
![]() $(\hat{X}_t)_{t\geq 0}$
with
$(\hat{X}_t)_{t\geq 0}$
with
![]() $\hat{X}_0\sim \pi ^{\mathrm{dis}}_G$
where we reject moves of the chain that lead to configurations outside of
$\hat{X}_0\sim \pi ^{\mathrm{dis}}_G$
where we reject moves of the chain that lead to configurations outside of
![]() $\Omega ^{\mathrm{dis}}$
. Note that
$\Omega ^{\mathrm{dis}}$
. Note that
![]() $\hat{X}_t\sim \pi ^{\mathrm{dis}}_G$
for all
$\hat{X}_t\sim \pi ^{\mathrm{dis}}_G$
for all
![]() $t\geq 0$
. We will show how to couple these two dynamics in
$t\geq 0$
. We will show how to couple these two dynamics in
![]() $O(n \log n)$
time. The result will follow by showing that there is a coupling between
$O(n \log n)$
time. The result will follow by showing that there is a coupling between
![]() $(X_t)_{t\geq 0}$
and
$(X_t)_{t\geq 0}$
and
![]() $(\hat{X}_t)_{t\geq 0}$
such that, for
$(\hat{X}_t)_{t\geq 0}$
such that, for
![]() $T=O(n\log n)$
, it holds that
$T=O(n\log n)$
, it holds that
Analogously to the ordered case we use the monotone coupling, where at every step
![]() $t$
, the two chains choose the same edge
$t$
, the two chains choose the same edge
![]() $e_t$
to update and use the same uniform number
$e_t$
to update and use the same uniform number
![]() $U_t\in [0,1]$
to decide whether to include
$U_t\in [0,1]$
to decide whether to include
![]() $e_t$
in each of
$e_t$
in each of
![]() $X_{t+1},\hat{X}_{t+1}$
. For
$X_{t+1},\hat{X}_{t+1}$
. For
![]() $t\geq 0$
, let
$t\geq 0$
, let
![]() $\mathcal{E}_t$
be the event that
$\mathcal{E}_t$
be the event that
![]() ${\mathrm{In}}(\hat{X}_t)\leq \zeta |E|$
and let
${\mathrm{In}}(\hat{X}_t)\leq \zeta |E|$
and let
![]() $\mathcal{E}_{\lt t}\;:\!=\;\bigcap _{t'=0,\ldots, t-1} \mathcal{E}_{t'}$
. From Lemma3 we have that
$\mathcal{E}_{\lt t}\;:\!=\;\bigcap _{t'=0,\ldots, t-1} \mathcal{E}_{t'}$
. From Lemma3 we have that
![]() $\pi ^{\mathrm{dis}}_G(\mathcal{E}_{\lt t})\geq 1-t\mathrm{e}^{-\Omega (n)}$
. Using again the monotonicity of the model for
$\pi ^{\mathrm{dis}}_G(\mathcal{E}_{\lt t})\geq 1-t\mathrm{e}^{-\Omega (n)}$
. Using again the monotonicity of the model for
![]() $q\geq 1$
, under the monotone coupling, for all
$q\geq 1$
, under the monotone coupling, for all
![]() $t\geq 0$
such that
$t\geq 0$
such that
![]() $\mathcal{E}_{\lt t}$
holds (and hence no reject move has happened in
$\mathcal{E}_{\lt t}$
holds (and hence no reject move has happened in
![]() $\hat{X}_t$
so far), we have that
$\hat{X}_t$
so far), we have that
![]() $X_t\leq \hat{X}_t$
(i.e.,
$X_t\leq \hat{X}_t$
(i.e.,
![]() ${\mathrm{In}}(X_t)\subseteq{\mathrm{In}}(\hat{X}_t)$
). We next proceed to bound the terms in the upper bound
${\mathrm{In}}(X_t)\subseteq{\mathrm{In}}(\hat{X}_t)$
). We next proceed to bound the terms in the upper bound
So, fix an arbitrary edge
![]() $e$
incident to some vertex
$e$
incident to some vertex
![]() $v$
, and let
$v$
, and let
![]() $(X^v_t)$
be the free RC dynamics on
$(X^v_t)$
be the free RC dynamics on
![]() $G[B_r(v)]$
. We couple the evolution of
$G[B_r(v)]$
. We couple the evolution of
![]() $(X_t^v)$
with that of
$(X_t^v)$
with that of
![]() $(X_t)$
and
$(X_t)$
and
![]() $(\hat{X}_t)$
using the monotone coupling analogously to the ordered case, where in
$(\hat{X}_t)$
using the monotone coupling analogously to the ordered case, where in
![]() $X_t^v$
we ignore updates of edges outside the ball
$X_t^v$
we ignore updates of edges outside the ball
![]() $G[B_r(v)]$
). We have
$G[B_r(v)]$
). We have
![]() $X_t^v\leq X_t$
for all
$X_t^v\leq X_t$
for all
![]() $t\geq 0$
, and hence, conditioned on
$t\geq 0$
, and hence, conditioned on
![]() $\mathcal{E}_{\lt t}$
, we have that
$\mathcal{E}_{\lt t}$
, we have that
![]() $X^v_t\leq X_t\leq \hat{X}_t$
. Proceeding as in the proof of Theorem11, we therefore get the following analogue of (5):
$X^v_t\leq X_t\leq \hat{X}_t$
. Proceeding as in the proof of Theorem11, we therefore get the following analogue of (5):
 \begin{equation} \begin{aligned}{\mathbb{P}}\big (X_t(e)\neq \hat{X}_t(e)\mid \mathcal{E}_{\lt t}\big )\leq 4{\mathbb{P}}\big (\overline{ \mathcal{E}_{\lt t}}\big )+\big |{\mathbb{P}}(X^v_t(e)&=0)-\pi _{{\mathcal{B}}^-_r(v)}(e\mapsto 0)\big |\\[5pt] &+\big |\pi _{{\mathcal{B}}^-_r(v)}(e\mapsto 0)-\pi ^{\mathrm{dis}}_G(e\mapsto 0)\big |. \end{aligned} \end{equation}
\begin{equation} \begin{aligned}{\mathbb{P}}\big (X_t(e)\neq \hat{X}_t(e)\mid \mathcal{E}_{\lt t}\big )\leq 4{\mathbb{P}}\big (\overline{ \mathcal{E}_{\lt t}}\big )+\big |{\mathbb{P}}(X^v_t(e)&=0)-\pi _{{\mathcal{B}}^-_r(v)}(e\mapsto 0)\big |\\[5pt] &+\big |\pi _{{\mathcal{B}}^-_r(v)}(e\mapsto 0)-\pi ^{\mathrm{dis}}_G(e\mapsto 0)\big |. \end{aligned} \end{equation}
Since
![]() $G$
has WSM within the disordered phase at radius
$G$
has WSM within the disordered phase at radius
![]() $r$
, we have that
$r$
, we have that
Let
![]() $C\gt 0$
be the constant in Lemma50 and set
$C\gt 0$
be the constant in Lemma50 and set
![]() $N_v=|E(B_r(v))|\leq \Delta ^{r+1}$
. By Chernoff bounds, for
$N_v=|E(B_r(v))|\leq \Delta ^{r+1}$
. By Chernoff bounds, for
![]() $T=\Theta (n\log n)$
, we get at least
$T=\Theta (n\log n)$
, we get at least
![]() $t_v\;:\!=\;\tfrac{40}{C}N_v\log n$
edge updates within the ball
$t_v\;:\!=\;\tfrac{40}{C}N_v\log n$
edge updates within the ball
![]() $B_r(v)$
with probability
$B_r(v)$
with probability
![]() $1-\exp (-n^{\Omega (1)})$
. Since
$1-\exp (-n^{\Omega (1)})$
. Since
![]() $r\leq \tfrac{1}{3}\log _{\Delta -1} n$
,
$r\leq \tfrac{1}{3}\log _{\Delta -1} n$
,
![]() $G[B_r(v)]$
is
$G[B_r(v)]$
is
![]() $K$
-treelike, so from Lemma50 and applying the log-Sobolev inequality (8) (with
$K$
-treelike, so from Lemma50 and applying the log-Sobolev inequality (8) (with
![]() $\gamma =C/(2N_v)$
,
$\gamma =C/(2N_v)$
,
![]() $t=t_v$
and
$t=t_v$
and
![]() $\min _{{\mathcal{F}}}\pi _{{\mathcal{B}}^-_r(v)}({\mathcal{F}})\geq (2q \mathrm{e}^{\beta })^{-N_v}$
), we have
$\min _{{\mathcal{F}}}\pi _{{\mathcal{B}}^-_r(v)}({\mathcal{F}})\geq (2q \mathrm{e}^{\beta })^{-N_v}$
), we have
where the last inequality holds for all
![]() $m=\Delta n=\Omega (1)$
. Plugging (11) and (12) into (10) for
$m=\Delta n=\Omega (1)$
. Plugging (11) and (12) into (10) for
![]() $t=T$
, and then back into (4), we get (9), that is,
$t=T$
, and then back into (4), we get (9), that is,
![]() ${\mathbb{P}}(X_T\neq \hat{X}_T)\leq 5m T \mathrm{e}^{-\Omega (n)}+m/m^3+1/100\leq 1/5$
. This finishes the proof of Theorem11.
${\mathbb{P}}(X_T\neq \hat{X}_T)\leq 5m T \mathrm{e}^{-\Omega (n)}+m/m^3+1/100\leq 1/5$
. This finishes the proof of Theorem11.
For the proof of Theorem13 (integer
![]() $q$
and
$q$
and
![]() $\beta \geq \beta _c$
), the argument is completely analogous to what was just presented for
$\beta \geq \beta _c$
), the argument is completely analogous to what was just presented for
![]() $\beta \leq \beta _c$
, using now the log-Sobolev bound of Lemma8 to get the analogue of (12) (see the proof in Section 2.4 and the inequality (7)).
$\beta \leq \beta _c$
, using now the log-Sobolev bound of Lemma8 to get the analogue of (12) (see the proof in Section 2.4 and the inequality (7)).
Appendix A. Mixing on tree-like graphs for the wired RC dynamics
In this section, we prove Lemma9 which we restate here for convenience.
Lemma 9.
Let
![]() $\Delta \geq 3$
be an integer, and
$\Delta \geq 3$
be an integer, and
![]() $q,K\gt 1$
,
$q,K\gt 1$
,
![]() $\beta \gt 0$
be reals. There exists
$\beta \gt 0$
be reals. There exists
![]() $\hat{C}\gt 0$
such that the following holds for any
$\hat{C}\gt 0$
such that the following holds for any
![]() $\Delta$
-regular graph
$\Delta$
-regular graph
![]() $G$
and integer
$G$
and integer
![]() $r\geq 1$
.
$r\geq 1$
.
Suppose that
![]() $\rho \in V$
is such that
$\rho \in V$
is such that
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. Then, with
$K$
-treelike. Then, with
![]() $n=|B_r(\rho )|$
, the mixing time of the free RC dynamics on
$n=|B_r(\rho )|$
, the mixing time of the free RC dynamics on
![]() $B_r(\rho )$
is
$B_r(\rho )$
is
![]() $\leq \hat{C}n\log n$
.
$\leq \hat{C}n\log n$
.
Proof. We use a canonical paths argument, following largely [Reference Mossel and Sly25, Proof of Lemma8]. Let
![]() $G=(V,E)$
be a
$G=(V,E)$
be a
![]() $\Delta$
-regular graph and
$\Delta$
-regular graph and
![]() $\rho \in V$
be such that
$\rho \in V$
be such that
![]() $G[B_r(\rho )]$
is
$G[B_r(\rho )]$
is
![]() $K$
-treelike. Let
$K$
-treelike. Let
![]() $n=|B_r(\rho )|$
,
$n=|B_r(\rho )|$
,
![]() $m=|E(B_r(\rho )|$
. Let
$m=|E(B_r(\rho )|$
. Let
![]() $\hat{\pi }=\hat{\pi }_{B_r(\rho )}$
be the stationary distribution of the wired RC dynamics on
$\hat{\pi }=\hat{\pi }_{B_r(\rho )}$
be the stationary distribution of the wired RC dynamics on
![]() $B_r(\rho )$
.
$B_r(\rho )$
.
Consider a BFS tree
![]() $T$
for
$T$
for
![]() $G[B_r(\rho )]$
starting from
$G[B_r(\rho )]$
starting from
![]() $\rho$
, let
$\rho$
, let
![]() $L$
be the set of the leaves of
$L$
be the set of the leaves of
![]() $T$
and let
$T$
and let
![]() $\mathcal{E}=E(G[B_r(\rho )])\backslash E(T)$
be the set of excess edges. Note that the height of
$\mathcal{E}=E(G[B_r(\rho )])\backslash E(T)$
be the set of excess edges. Note that the height of
![]() $T$
is at most
$T$
is at most
![]() $r$
, the set
$r$
, the set
![]() $S_r(\rho )$
of vertices at distance
$S_r(\rho )$
of vertices at distance
![]() $r$
from
$r$
from
![]() $\rho$
satisfies
$\rho$
satisfies
![]() $S_r(\rho )\subseteq L$
and there are at most
$S_r(\rho )\subseteq L$
and there are at most
![]() $2K$
leaves of
$2K$
leaves of
![]() $T$
at depth less than
$T$
at depth less than
![]() $r$
(by the
$r$
(by the
![]() $\Delta$
-regularity of
$\Delta$
-regularity of
![]() $G$
, each such leaf must be incident to an excess edge of
$G$
, each such leaf must be incident to an excess edge of
![]() $G$
), so
$G$
), so
![]() $|L\backslash S_r(\rho )|\leq 2K$
. For a vertex
$|L\backslash S_r(\rho )|\leq 2K$
. For a vertex
![]() $u$
in
$u$
in
![]() $B_r(\rho )$
, we let
$B_r(\rho )$
, we let
![]() $T_u$
be the subtree of
$T_u$
be the subtree of
![]() $T$
rooted at
$T$
rooted at
![]() $u$
, and
$u$
, and
![]() $\mathrm{Anc}(u)$
be the ancestors of
$\mathrm{Anc}(u)$
be the ancestors of
![]() $u$
in
$u$
in
![]() $T$
(i.e., the vertices on the path from the root
$T$
(i.e., the vertices on the path from the root
![]() $\rho$
to
$\rho$
to
![]() $u$
, including
$u$
, including
![]() $u$
).
$u$
).
Consider next a depth-first-search traversal of the tree
![]() $T$
starting from
$T$
starting from
![]() $\rho$
, and let
$\rho$
, and let
![]() $v_1,\ldots, v_n$
be the order in which the vertices of
$v_1,\ldots, v_n$
be the order in which the vertices of
![]() $T$
were first visited. We write
$T$
were first visited. We write
![]() $v_i\lt v_j$
whenever
$v_i\lt v_j$
whenever
![]() $i\lt j$
; moreover, for a subset of vertices
$i\lt j$
; moreover, for a subset of vertices
![]() $S$
and a vertex
$S$
and a vertex
![]() $u$
, we write
$u$
, we write
![]() $S\lt u$
to denote that for each
$S\lt u$
to denote that for each
![]() $w\in S$
it holds that
$w\in S$
it holds that
![]() $w\lt u$
. Since the tree
$w\lt u$
. Since the tree
![]() $T$
has depth
$T$
has depth
![]() $r$
, at any stage of the DFS traversal there are at most
$r$
, at any stage of the DFS traversal there are at most
![]() $r$
vertices which are visited but not fully explored (note that a leaf that is visited is automatically explored). Since the degree of any vertex is
$r$
vertices which are visited but not fully explored (note that a leaf that is visited is automatically explored). Since the degree of any vertex is
![]() $\leq \Delta$
, it follows that
$\leq \Delta$
, it follows that
-
(a) for
 $i=1,\ldots, n$
, there are at most
$i=1,\ldots, n$
, there are at most
 $\Delta r$
tree edges with one endpoint in
$\Delta r$
tree edges with one endpoint in
 $\{v_1,\ldots, v_i\}$
and the other in
$\{v_1,\ldots, v_i\}$
and the other in
 $\{v_{i+1},\ldots, v_m\}$
(from the DFS traversal).
$\{v_{i+1},\ldots, v_m\}$
(from the DFS traversal). -
(b) for an arbitrary vertex
 $u$
in
$u$
in
 $T$
and any vertex
$T$
and any vertex
 $w$
which is not an ancestor of
$w$
which is not an ancestor of
 $u$
(i.e.,
$u$
(i.e.,
 $w\notin \mathrm{Anc}(u)$
), we have from the DFS traversal either that
$w\notin \mathrm{Anc}(u)$
), we have from the DFS traversal either that
 $V(T_w)\lt u$
or
$V(T_w)\lt u$
or
 $V(T_w) \gt u$
.
$V(T_w) \gt u$
.
We order the edges
![]() $e_1,\ldots, e_m$
in
$e_1,\ldots, e_m$
in
![]() $G[{\mathcal{B}}_r(\rho )]$
(including excess edges) in lexicographic order in terms of the order of the vertices. So edges with an endpoint
$G[{\mathcal{B}}_r(\rho )]$
(including excess edges) in lexicographic order in terms of the order of the vertices. So edges with an endpoint
![]() $v_1$
come first (ordered by the other endpoint) and so on.
$v_1$
come first (ordered by the other endpoint) and so on.
For two configurations
![]() ${\mathcal{F}},{\mathcal{F}}':E\rightarrow \{0,1\}$
that differ on the edges
${\mathcal{F}},{\mathcal{F}}':E\rightarrow \{0,1\}$
that differ on the edges
![]() $e_{i_1},\ldots, e_{i_k}$
(with
$e_{i_1},\ldots, e_{i_k}$
(with
![]() $i_1\lt \cdots \lt i_k$
), define the path
$i_1\lt \cdots \lt i_k$
), define the path
![]() $\mathrm{Path}({\mathcal{F}},{\mathcal{F}}')$
of configurations
$\mathrm{Path}({\mathcal{F}},{\mathcal{F}}')$
of configurations
![]() $\mathrm{Path}({\mathcal{F}},{\mathcal{F}}')={\mathcal{F}}_0\rightarrow{\mathcal{F}}_1\cdots \rightarrow{\mathcal{F}}_{k}$
by defining, for
$\mathrm{Path}({\mathcal{F}},{\mathcal{F}}')={\mathcal{F}}_0\rightarrow{\mathcal{F}}_1\cdots \rightarrow{\mathcal{F}}_{k}$
by defining, for
![]() $j=0,\ldots, k$
,
$j=0,\ldots, k$
,
![]() ${\mathcal{F}}_{j}$
to agree with
${\mathcal{F}}_{j}$
to agree with
![]() $\mathcal{F}$
on the edges
$\mathcal{F}$
on the edges
![]() $\{e_{i_{j+1}},\ldots, e_{i_k}\}$
and to agree with
$\{e_{i_{j+1}},\ldots, e_{i_k}\}$
and to agree with
![]() ${\mathcal{F}}'$
on the edges
${\mathcal{F}}'$
on the edges
![]() $\{e_{i_1},\ldots, e_{i_j}\}$
. Note that
$\{e_{i_1},\ldots, e_{i_j}\}$
. Note that
![]() ${\mathcal{F}}_0={\mathcal{F}},{\mathcal{F}}_k={\mathcal{F}}'$
and both
${\mathcal{F}}_0={\mathcal{F}},{\mathcal{F}}_k={\mathcal{F}}'$
and both
![]() ${\mathcal{F}},{\mathcal{F}}'$
and hence
${\mathcal{F}},{\mathcal{F}}'$
and hence
![]() ${\mathcal{F}}_j$
as well agree on
${\mathcal{F}}_j$
as well agree on
![]() $E\backslash \{e_{i_1},\ldots, e_{i_k}\})$
. Then, the relaxation time of the chain, see for example [Reference Jerrum23, Chapter 5], is bounded by
$E\backslash \{e_{i_1},\ldots, e_{i_k}\})$
. Then, the relaxation time of the chain, see for example [Reference Jerrum23, Chapter 5], is bounded by
 \begin{equation*}\tau \leq m\max _{({\mathcal {F}},{\mathcal {F}}')}\sum _{\substack {{\mathcal {A}},{\mathcal {A}}':E\rightarrow \{0,1\};\\[5pt] ({\mathcal {F}}\rightarrow {\mathcal {F}}')\in \mathrm {Path}({\mathcal {A}},{\mathcal {A}}')}}\frac {\hat {\pi }({\mathcal {A}})\hat {\pi }({\mathcal {A}}')}{\hat {\pi }({\mathcal {F}}){\mathbb {P}}({\mathcal {F}},{\mathcal {F}}')},\end{equation*}
\begin{equation*}\tau \leq m\max _{({\mathcal {F}},{\mathcal {F}}')}\sum _{\substack {{\mathcal {A}},{\mathcal {A}}':E\rightarrow \{0,1\};\\[5pt] ({\mathcal {F}}\rightarrow {\mathcal {F}}')\in \mathrm {Path}({\mathcal {A}},{\mathcal {A}}')}}\frac {\hat {\pi }({\mathcal {A}})\hat {\pi }({\mathcal {A}}')}{\hat {\pi }({\mathcal {F}}){\mathbb {P}}({\mathcal {F}},{\mathcal {F}}')},\end{equation*}
where the maximum is over all pairs of configurations
![]() ${\mathcal{F}},{\mathcal{F}}'$
that differ on a single edge and the summation is over all pairs of configurations
${\mathcal{F}},{\mathcal{F}}'$
that differ on a single edge and the summation is over all pairs of configurations
![]() ${\mathcal{A}},{\mathcal{A}}'$
whose corresponding
${\mathcal{A}},{\mathcal{A}}'$
whose corresponding
![]() $\mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
includes the transition
$\mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
includes the transition
![]() ${\mathcal{F}}\rightarrow{\mathcal{F}}'$
as part of the path.
${\mathcal{F}}\rightarrow{\mathcal{F}}'$
as part of the path.
Consider an arbitrary pair of configurations
![]() $\kappa =({\mathcal{F}},{\mathcal{F}}')$
that differ at a single edge
$\kappa =({\mathcal{F}},{\mathcal{F}}')$
that differ at a single edge
![]() $f=\{v_j, v_{j'}\}$
for some
$f=\{v_j, v_{j'}\}$
for some
![]() $j\lt j'$
and suppose further that
$j\lt j'$
and suppose further that
![]() $f=e_\ell$
. For configurations
$f=e_\ell$
. For configurations
![]() ${\mathcal{A}},{\mathcal{A}}'$
such that
${\mathcal{A}},{\mathcal{A}}'$
such that
![]() $({\mathcal{F}}\rightarrow{\mathcal{F}}')\in \mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
define the configuration
$({\mathcal{F}}\rightarrow{\mathcal{F}}')\in \mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
define the configuration
![]() $g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
so that
$g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
so that
From the fact that
![]() $({\mathcal{F}}\rightarrow{\mathcal{F}}')\in \mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
, we also have that:
$({\mathcal{F}}\rightarrow{\mathcal{F}}')\in \mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
, we also have that:
It follows that the map
![]() $g_{\kappa }(\cdot, \cdot )$
is injective, that is, given its value
$g_{\kappa }(\cdot, \cdot )$
is injective, that is, given its value
![]() ${\mathcal{F}}^*$
and the configurations
${\mathcal{F}}^*$
and the configurations
![]() ${\mathcal{F}},{\mathcal{F}}'$
, there is a unique pair
${\mathcal{F}},{\mathcal{F}}'$
, there is a unique pair
![]() $({\mathcal{A}},{\mathcal{A}}')$
such that
$({\mathcal{A}},{\mathcal{A}}')$
such that
![]() ${\mathcal{F}}^*=g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
and
${\mathcal{F}}^*=g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
and
![]() $({\mathcal{F}}\rightarrow{\mathcal{F}}')\in \mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
. For a configuration
$({\mathcal{F}}\rightarrow{\mathcal{F}}')\in \mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
. For a configuration
![]() $\mathcal{X}\;:\; E(B_r(\rho ))\rightarrow \{0,1\}$
, let
$\mathcal{X}\;:\; E(B_r(\rho ))\rightarrow \{0,1\}$
, let
![]() $\hat{c}(\mathcal{X})$
denote the number of components in
$\hat{c}(\mathcal{X})$
denote the number of components in
![]() $(B_r(\rho ),{\mathrm{In}}(X))$
that do not include any of the vertices in
$(B_r(\rho ),{\mathrm{In}}(X))$
that do not include any of the vertices in
![]() $S_r(\rho )$
, cf. Footnote 5. Let
$S_r(\rho )$
, cf. Footnote 5. Let
![]() $s\;:\!=\; \Delta r + K$
and
$s\;:\!=\; \Delta r + K$
and
![]() $t \;:\!=\; 4 \Delta r + 12 K$
. The main step in the proof is to show that:
$t \;:\!=\; 4 \Delta r + 12 K$
. The main step in the proof is to show that:
Assuming these for the moment, we have that
Recall that
![]() $p=1-\mathrm{e}^{-\beta }$
and that for
$p=1-\mathrm{e}^{-\beta }$
and that for
![]() $q\gt 1$
it holds that
$q\gt 1$
it holds that
![]() $\hat{p}\in (p/q,p)$
. Therefore, for the RC dynamics, we have that
$\hat{p}\in (p/q,p)$
. Therefore, for the RC dynamics, we have that
![]() ${\mathbb{P}}({\mathcal{F}},{\mathcal{F}}')\geq \frac{\min \{p/q,(1-p)\}}{m} \geq (1-\mathrm{e}^{-\beta })/(q m \mathrm{e}^\beta )$
using that
${\mathbb{P}}({\mathcal{F}},{\mathcal{F}}')\geq \frac{\min \{p/q,(1-p)\}}{m} \geq (1-\mathrm{e}^{-\beta })/(q m \mathrm{e}^\beta )$
using that
![]() $\min \{p/q,(1-p)\}\geq \mathrm{e}^{-\beta }/q$
. Using this and the injectivity of
$\min \{p/q,(1-p)\}\geq \mathrm{e}^{-\beta }/q$
. Using this and the injectivity of
![]() $g$
, we can bound
$g$
, we can bound
![]() $\tau$
by
$\tau$
by
 \begin{equation*}\tau \leq \frac {m^2 q^{t+1}\mathrm {e}^{\beta (s+1)}} {(1-\mathrm {e}^{-\beta })} \sum _{\substack {{\mathcal {A}},{\mathcal {A}}':E\rightarrow \{0,1\};\\[5pt] ({\mathcal {F}}\rightarrow {\mathcal {F}}')\in \mathrm {Path}({\mathcal {A}},{\mathcal {A}}')}} \hat {\pi }\big (g_{\kappa }({\mathcal {A}},{\mathcal {A}}')\big )\leq \frac {m^2 q^{t+1}\mathrm {e}^{\beta (s+1)}} {(1-\mathrm {e}^{-\beta })}.\end{equation*}
\begin{equation*}\tau \leq \frac {m^2 q^{t+1}\mathrm {e}^{\beta (s+1)}} {(1-\mathrm {e}^{-\beta })} \sum _{\substack {{\mathcal {A}},{\mathcal {A}}':E\rightarrow \{0,1\};\\[5pt] ({\mathcal {F}}\rightarrow {\mathcal {F}}')\in \mathrm {Path}({\mathcal {A}},{\mathcal {A}}')}} \hat {\pi }\big (g_{\kappa }({\mathcal {A}},{\mathcal {A}}')\big )\leq \frac {m^2 q^{t+1}\mathrm {e}^{\beta (s+1)}} {(1-\mathrm {e}^{-\beta })}.\end{equation*}
The mixing time is at most
![]() $ \tau (1 + \tfrac 12 \log (\min _{\mathcal{X}} \hat{\pi }(\mathcal{X})^{-1}))$
Since
$ \tau (1 + \tfrac 12 \log (\min _{\mathcal{X}} \hat{\pi }(\mathcal{X})^{-1}))$
Since
![]() $\min _{\mathcal{X}}\hat{\pi }(\mathcal{X})\geq 2^{-n} q^{-n} e^{-\beta m}$
and
$\min _{\mathcal{X}}\hat{\pi }(\mathcal{X})\geq 2^{-n} q^{-n} e^{-\beta m}$
and
![]() $m\leq \Delta n$
, the mixing time is at most
$m\leq \Delta n$
, the mixing time is at most
![]() $n^3 \Delta ^2 q^{t+1}\mathrm{e}^{\beta (s+1)}\tfrac{1+ \log (q) + \beta \Delta }{1-\mathrm{e}^{-\beta }}$
so the statement for the mixing time follows by taking
$n^3 \Delta ^2 q^{t+1}\mathrm{e}^{\beta (s+1)}\tfrac{1+ \log (q) + \beta \Delta }{1-\mathrm{e}^{-\beta }}$
so the statement for the mixing time follows by taking
![]() $ \hat{C}\;:\!=\; 2 \Delta ^3 (q \mathrm{e}^{\beta })^{12K+3}/{(1-\mathrm{e}^{-\beta })}$
.
$ \hat{C}\;:\!=\; 2 \Delta ^3 (q \mathrm{e}^{\beta })^{12K+3}/{(1-\mathrm{e}^{-\beta })}$
.
It remains to show (15) and (16). For convenience let
![]() ${\mathcal{F}}^*=g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
. We will shortly prove the following facts for an arbitrary edge
${\mathcal{F}}^*=g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
. We will shortly prove the following facts for an arbitrary edge
![]() $e=\{u,w\}$
:
$e=\{u,w\}$
:
-
1. if
 ${\mathcal{A}}(e)={\mathcal{A}}'(e)$
, then
${\mathcal{A}}(e)={\mathcal{A}}'(e)$
, then
 ${\mathcal{A}}(e)={\mathcal{A}}'(e)={\mathcal{F}}(e)={\mathcal{F}}^*(e)$
.
${\mathcal{A}}(e)={\mathcal{A}}'(e)={\mathcal{F}}(e)={\mathcal{F}}^*(e)$
. -
2. if
 ${\mathcal{A}}(e)\neq{\mathcal{A}}'(e)$
, then
${\mathcal{A}}(e)\neq{\mathcal{A}}'(e)$
, then
 $\big ({\mathcal{A}}(e),{\mathcal{A}}'(e)\big )= \big ({\mathcal{F}}^*(e),{\mathcal{F}}(e)\big )$
when
$\big ({\mathcal{A}}(e),{\mathcal{A}}'(e)\big )= \big ({\mathcal{F}}^*(e),{\mathcal{F}}(e)\big )$
when
 $u,w\leq v_j$
and
$u,w\leq v_j$
and
 $\big ({\mathcal{A}}(e),{\mathcal{A}}'(e)\big )= \big ({\mathcal{F}}(e),{\mathcal{F}}^*(e)\big )$
when
$\big ({\mathcal{A}}(e),{\mathcal{A}}'(e)\big )= \big ({\mathcal{F}}(e),{\mathcal{F}}^*(e)\big )$
when
 $u,w\gt v_j$
.
$u,w\gt v_j$
.
Indeed, for Item 1, consider
![]() $e$
with
$e$
with
![]() ${\mathcal{A}}(e) ={\mathcal{A}}'(e)$
and suppose first that
${\mathcal{A}}(e) ={\mathcal{A}}'(e)$
and suppose first that
![]() ${\mathcal{A}}(e)={\mathcal{A}}'(e)=1$
. Then
${\mathcal{A}}(e)={\mathcal{A}}'(e)=1$
. Then
![]() ${\mathcal{F}}(e)={\mathcal{F}}'(e)=1$
(since by the construction of
${\mathcal{F}}(e)={\mathcal{F}}'(e)=1$
(since by the construction of
![]() $\mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
, all configurations in it agree on the edges where
$\mathrm{Path}({\mathcal{A}},{\mathcal{A}}')$
, all configurations in it agree on the edges where
![]() ${\mathcal{A}},{\mathcal{A}}'$
agree). Moreover,
${\mathcal{A}},{\mathcal{A}}'$
agree). Moreover,
![]() ${\mathcal{F}}^*(e)=1$
by construction (since
${\mathcal{F}}^*(e)=1$
by construction (since
![]() ${\mathcal{F}}^*=g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
agrees with
${\mathcal{F}}^*=g_{\kappa }({\mathcal{A}},{\mathcal{A}}')$
agrees with
![]() ${\mathcal{A}},{\mathcal{A}}'$
on the edges where the latter agree). The proof for the second case
${\mathcal{A}},{\mathcal{A}}'$
on the edges where the latter agree). The proof for the second case
![]() ${\mathcal{A}}(e)={\mathcal{A}}'(e)=0$
is analogous. Item 2 follows from (13) and (14) after observing that
${\mathcal{A}}(e)={\mathcal{A}}'(e)=0$
is analogous. Item 2 follows from (13) and (14) after observing that
![]() $u,w\leq v_j$
implies that
$u,w\leq v_j$
implies that
![]() $e=\{u,w\}\lt e_\ell$
, while
$e=\{u,w\}\lt e_\ell$
, while
![]() $u,w\gt v_j$
gives that
$u,w\gt v_j$
gives that
![]() $e\gt e_\ell$
.
$e\gt e_\ell$
.
Let
![]() $W_j$
be the tree edges which are incident to a vertex in
$W_j$
be the tree edges which are incident to a vertex in
![]() $\mathrm{Anc}(v_j)$
, so that
$\mathrm{Anc}(v_j)$
, so that
![]() $|W_j|\leq \Delta r$
. From Item (1), these are the only tree edges that can have one endpoint in
$|W_j|\leq \Delta r$
. From Item (1), these are the only tree edges that can have one endpoint in
![]() $\{v_1,\ldots, v_j\}$
and the other among
$\{v_1,\ldots, v_j\}$
and the other among
![]() $\{v_{j+1},\ldots, v_n\}$
, along with any non-tree edges (i.e., excess edges
$\{v_{j+1},\ldots, v_n\}$
, along with any non-tree edges (i.e., excess edges
![]() $\mathcal{E}$
). Therefore, from Items 1 and 2 above, it follows that for an edge
$\mathcal{E}$
). Therefore, from Items 1 and 2 above, it follows that for an edge
![]() $e\in E\backslash (W_j \cup \mathcal{E})$
it holds that
$e\in E\backslash (W_j \cup \mathcal{E})$
it holds that
which establishes (15) since
![]() $|W_j \cup \mathcal{E}|\leq \Delta r+K$
.
$|W_j \cup \mathcal{E}|\leq \Delta r+K$
.
To show (16), fix an arbitrary root-to-leaf path
![]() $P$
passing through
$P$
passing through
![]() $v_j$
, and denote by
$v_j$
, and denote by
![]() $E_P$
be the edges of the path. Now, consider the slightly ‘tweaked’ configurations
$E_P$
be the edges of the path. Now, consider the slightly ‘tweaked’ configurations
![]() $\hat{{\mathcal{A}}},\hat{{\mathcal{A}}}',\hat{{\mathcal{F}}},\hat{{\mathcal{F}}}^*$
obtained from
$\hat{{\mathcal{A}}},\hat{{\mathcal{A}}}',\hat{{\mathcal{F}}},\hat{{\mathcal{F}}}^*$
obtained from
![]() ${\mathcal{A}},{\mathcal{A}}',{\mathcal{F}},{\mathcal{F}}^*$
, respectively, by setting, for each
${\mathcal{A}},{\mathcal{A}}',{\mathcal{F}},{\mathcal{F}}^*$
, respectively, by setting, for each
![]() $\mathcal{X}\in \{{\mathcal{A}},{\mathcal{A}}',{\mathcal{F}},{\mathcal{F}}^*\}$
,
$\mathcal{X}\in \{{\mathcal{A}},{\mathcal{A}}',{\mathcal{F}},{\mathcal{F}}^*\}$
,
![]() $\hat{\mathcal{X}}(e)=1$
for
$\hat{\mathcal{X}}(e)=1$
for
![]() $e\in E_P\cup W_j$
,
$e\in E_P\cup W_j$
,
![]() $\hat{\mathcal{X}}(e)=0$
for
$\hat{\mathcal{X}}(e)=0$
for
![]() $e\in \mathcal{E}$
and
$e\in \mathcal{E}$
and
![]() $\hat{\mathcal{X}}(e)=\mathcal{X}(e)$
for
$\hat{\mathcal{X}}(e)=\mathcal{X}(e)$
for
![]() $e\notin E_P\cup W_j\cup \mathcal{E}$
. Note that, for each
$e\notin E_P\cup W_j\cup \mathcal{E}$
. Note that, for each
![]() $\mathcal{X}\in \{{\mathcal{A}},{\mathcal{A}}',{\mathcal{F}},{\mathcal{F}}^*\}$
, we have
$\mathcal{X}\in \{{\mathcal{A}},{\mathcal{A}}',{\mathcal{F}},{\mathcal{F}}^*\}$
, we have
![]() $\big ||\hat{\mathcal{X}}|-|\mathcal{X}|\big |\leq \Delta r+K$
, so
$\big ||\hat{\mathcal{X}}|-|\mathcal{X}|\big |\leq \Delta r+K$
, so
![]() $\big ||\hat{c}(\hat{\mathcal{X}})|-|\hat{c}(\mathcal{X})|\big |\leq \Delta r+K$
as well. So, to prove (16), it suffices to show
$\big ||\hat{c}(\hat{\mathcal{X}})|-|\hat{c}(\mathcal{X})|\big |\leq \Delta r+K$
as well. So, to prove (16), it suffices to show
To show this, first note that
![]() $\hat{{\mathcal{A}}},\hat{{\mathcal{A}}}',\hat{{\mathcal{F}}},\hat{{\mathcal{F}}}^*$
still satisfy Items 1 and 2 above (replacing
$\hat{{\mathcal{A}}},\hat{{\mathcal{A}}}',\hat{{\mathcal{F}}},\hat{{\mathcal{F}}}^*$
still satisfy Items 1 and 2 above (replacing
![]() $\mathcal{A}$
with
$\mathcal{A}$
with
![]() $\hat{\mathcal{A}}$
, and so on) since the only changes are for edges in
$\hat{\mathcal{A}}$
, and so on) since the only changes are for edges in
![]() $E_P\cup W_j\cup \mathcal{E}$
on which the assignments of the tweaked configurations are identical (and hence fall under Item 1). In fact, Items 1 and 2 now apply to all edges for the tweaked configurations (previously, edges in
$E_P\cup W_j\cup \mathcal{E}$
on which the assignments of the tweaked configurations are identical (and hence fall under Item 1). In fact, Items 1 and 2 now apply to all edges for the tweaked configurations (previously, edges in
![]() $W_j\cup \mathcal{E}$
were potentially not covered in Item 2, but now are covered since they fall under Item 1). So, the analogue of (17) for
$W_j\cup \mathcal{E}$
were potentially not covered in Item 2, but now are covered since they fall under Item 1). So, the analogue of (17) for
![]() $\hat{{\mathcal{A}}},\hat{{\mathcal{A}}}',\hat{{\mathcal{F}}},\hat{{\mathcal{F}}}^*$
holds for every edge of
$\hat{{\mathcal{A}}},\hat{{\mathcal{A}}}',\hat{{\mathcal{F}}},\hat{{\mathcal{F}}}^*$
holds for every edge of
![]() $G[B_r(\rho )]$
, yielding that
$G[B_r(\rho )]$
, yielding that
and, further, for any edge
![]() $e=\{u,w\}$
we have that
$e=\{u,w\}$
we have that
 \begin{equation} \big (\hat{\mathcal{A}}(e),\hat{\mathcal{A}}'(e)\big )=\begin{cases} \big (\hat{\mathcal{F}}^*(e),\hat{\mathcal{F}}(e)\big ) & \mbox{ if } u,w\leq v_j\\[5pt] \big (\hat{\mathcal{F}}(e),\hat{\mathcal{F}}^*(e)\big ),& \mbox{ otherwise. } \end{cases} \end{equation}
\begin{equation} \big (\hat{\mathcal{A}}(e),\hat{\mathcal{A}}'(e)\big )=\begin{cases} \big (\hat{\mathcal{F}}^*(e),\hat{\mathcal{F}}(e)\big ) & \mbox{ if } u,w\leq v_j\\[5pt] \big (\hat{\mathcal{F}}(e),\hat{\mathcal{F}}^*(e)\big ),& \mbox{ otherwise. } \end{cases} \end{equation}
At this stage, it will be convenient to consider the graph
![]() $T^*$
obtained from
$T^*$
obtained from
![]() $G[B_r(\rho )]$
by identifying all the leaves of
$G[B_r(\rho )]$
by identifying all the leaves of
![]() $T$
into a single vertex
$T$
into a single vertex
![]() $v^*$
(recall that the leaves of
$v^*$
(recall that the leaves of
![]() $T$
consist of the vertices
$T$
consist of the vertices
![]() $S_r(\rho )$
, which are at depth
$S_r(\rho )$
, which are at depth
![]() $r$
, together with at most
$r$
, together with at most
![]() $2K$
leaves that are at depth
$2K$
leaves that are at depth
![]() $\lt r$
). For
$\lt r$
). For
![]() $\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
, let
$\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
, let
![]() $c^*(\mathcal{X})$
be the number of components in the graph
$c^*(\mathcal{X})$
be the number of components in the graph
![]() $T^*[{\mathrm{In}}(\mathcal{X})]$
that do not include
$T^*[{\mathrm{In}}(\mathcal{X})]$
that do not include
![]() $v^*$
and let
$v^*$
and let
![]() ${\mathcal{C}}^*(\mathcal{X})=(V^*(\mathcal{X}),E^*(\mathcal{X}))$
be the connected component of
${\mathcal{C}}^*(\mathcal{X})=(V^*(\mathcal{X}),E^*(\mathcal{X}))$
be the connected component of
![]() $v^*$
. Note that any connected component of
$v^*$
. Note that any connected component of
![]() $(B_r(\rho ),{\mathrm{In}}(\mathcal{X}))$
that does not include a vertex from
$(B_r(\rho ),{\mathrm{In}}(\mathcal{X}))$
that does not include a vertex from
![]() $S_r(\rho )$
is not connected to
$S_r(\rho )$
is not connected to
![]() $v^*$
in
$v^*$
in
![]() $T^*[{\mathrm{In}}(\mathcal{X})]$
, unless it contains one of the
$T^*[{\mathrm{In}}(\mathcal{X})]$
, unless it contains one of the
![]() $2K$
leaves at depth
$2K$
leaves at depth
![]() $\lt r$
. It follows that
$\lt r$
. It follows that
![]() $|c^*(\mathcal{X})-\hat{c}(\mathcal{X})|\leq 2K$
, so to prove (18) it suffices to show
$|c^*(\mathcal{X})-\hat{c}(\mathcal{X})|\leq 2K$
, so to prove (18) it suffices to show
For
![]() $\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
, note that a connected component
$\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
, note that a connected component
![]() $F$
of
$F$
of
![]() $\mathcal{X}$
that does not include
$\mathcal{X}$
that does not include
![]() $v^*$
is a subgraph of
$v^*$
is a subgraph of
![]() $T$
(using that
$T$
(using that
![]() $\mathcal{X}(e)=0$
for
$\mathcal{X}(e)=0$
for
![]() $e\in \mathcal{E}$
) and hence a tree, so
$e\in \mathcal{E}$
) and hence a tree, so
![]() $1=|V(F)|-|E(F)|$
. Summing over all such components, we obtain that
$1=|V(F)|-|E(F)|$
. Summing over all such components, we obtain that
Therefore, using (19), to finish the proof of (21) it suffices to show that for an arbitrary vertex
![]() $v$
and an arbitrary edge
$v$
and an arbitrary edge
![]() $e$
it holds that
$e$
it holds that
Clearly (22) is true for any
![]() $v\in \mathrm{Anc}(v_j)$
since
$v\in \mathrm{Anc}(v_j)$
since
![]() $v\in{\mathcal{C}}(\mathcal{X})$
for each
$v\in{\mathcal{C}}(\mathcal{X})$
for each
![]() $\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
by construction of the tweaked configurations. So, consider
$\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
by construction of the tweaked configurations. So, consider
![]() $v\notin \mathrm{Anc}(v_j)$
. First, suppose
$v\notin \mathrm{Anc}(v_j)$
. First, suppose
![]() $v\lt v_j$
. Let
$v\lt v_j$
. Let
![]() $u$
be the ancestor of
$u$
be the ancestor of
![]() $v$
whose parent
$v$
whose parent
![]() $w$
is an ancestor of
$w$
is an ancestor of
![]() $v_j$
. The key point is that for each
$v_j$
. The key point is that for each
![]() $\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
we have
$\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
we have
![]() $w\in V^*(\mathcal{X})$
(since
$w\in V^*(\mathcal{X})$
(since
![]() $w$
is an ancestor of
$w$
is an ancestor of
![]() $v_j$
) and the edge
$v_j$
) and the edge
![]() $e=\{u,w\}$
belongs to
$e=\{u,w\}$
belongs to
![]() $W_j$
, so
$W_j$
, so
![]() $\hat{\mathcal{X}}(e)=1$
. Therefore whether
$\hat{\mathcal{X}}(e)=1$
. Therefore whether
![]() $v \in V^*(\mathcal{X})$
is determined by the set of those paths contained in the subtree
$v \in V^*(\mathcal{X})$
is determined by the set of those paths contained in the subtree
![]() $T_u$
which start from
$T_u$
which start from
![]() $v$
and end either at
$v$
and end either at
![]() $u$
or a leaf of
$u$
or a leaf of
![]() $T_u$
. Denote by
$T_u$
. Denote by
![]() $\mathcal{P}_{v}$
the set of all such paths. Since
$\mathcal{P}_{v}$
the set of all such paths. Since
![]() $v\lt v_j$
, we have that
$v\lt v_j$
, we have that
![]() $u\lt v_j$
and that
$u\lt v_j$
and that
![]() $u$
is not ancestor of
$u$
is not ancestor of
![]() $v_j$
, so from Item 2 it holds that
$v_j$
, so from Item 2 it holds that
![]() $V(T_u)\lt v_j$
. It follows from (20) that for every edge
$V(T_u)\lt v_j$
. It follows from (20) that for every edge
![]() $e\in E(T_u)$
we have
$e\in E(T_u)$
we have
![]() $(\hat{\mathcal{A}}(e),\hat{\mathcal{A}}'(e))=({\mathcal{F}}^*(e),\hat{\mathcal{F}}^*(e))$
, so
$(\hat{\mathcal{A}}(e),\hat{\mathcal{A}}'(e))=({\mathcal{F}}^*(e),\hat{\mathcal{F}}^*(e))$
, so
and similarly
![]() $ v\in V^*(\hat{\mathcal{A}}')\Leftrightarrow v\in V^*(\hat{\mathcal{F}})$
, proving (22) for
$ v\in V^*(\hat{\mathcal{A}}')\Leftrightarrow v\in V^*(\hat{\mathcal{F}})$
, proving (22) for
![]() $v\lt v_j$
. An analogous argument applies when
$v\lt v_j$
. An analogous argument applies when
![]() $v\gt v_j$
, then
$v\gt v_j$
, then
![]() $V(T_u)\gt v_j$
and, using (20) again,
$V(T_u)\gt v_j$
and, using (20) again,
![]() $v\in V^*(\hat{\mathcal{A}})\Leftrightarrow v\in V^*(\hat{\mathcal{F}})$
,
$v\in V^*(\hat{\mathcal{A}})\Leftrightarrow v\in V^*(\hat{\mathcal{F}})$
,
![]() $ v\in V^*(\hat{\mathcal{A}}')\Leftrightarrow v\in V^*(\hat{\mathcal{F}}^*)$
, finishing the proof of (22). The proof of (23) is very similar, after noting that for
$ v\in V^*(\hat{\mathcal{A}}')\Leftrightarrow v\in V^*(\hat{\mathcal{F}}^*)$
, finishing the proof of (22). The proof of (23) is very similar, after noting that for
![]() $\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
and an edge
$\mathcal{X}\in \{\hat{\mathcal{A}},\hat{\mathcal{A}}',\hat{\mathcal{F}},\hat{\mathcal{F}}^*\}$
and an edge
![]() $e=\{u,w\}$
it holds that
$e=\{u,w\}$
it holds that
![]() $e\in E^*(\mathcal{X})$
iff
$e\in E^*(\mathcal{X})$
iff
![]() $ \mathcal{X}(e)=1$
and
$ \mathcal{X}(e)=1$
and
![]() $u,w\in V^*(\mathcal{X})$
.
$u,w\in V^*(\mathcal{X})$
.
This completes the proof of (21), and hence the proof of (18) and (16) as well, concluding therefore the lemma.
Appendix B. Boundary conditions and monotonicity
We will be interested in vertices on the boundary of a partial configuration, and in the structure of connected components in the graph induced by in-edges. See Definition39.
Observation 51.
Let
![]() ${\mathcal{F}}_1$
and
${\mathcal{F}}_1$
and
![]() ${\mathcal{F}}_2$
be two partial configurations such that
${\mathcal{F}}_2$
be two partial configurations such that
![]() $R({\mathcal{F}}_1) = R({\mathcal{F}}_2)$
and
$R({\mathcal{F}}_1) = R({\mathcal{F}}_2)$
and
![]() $\xi ({\mathcal{F}}_1)=\xi ({\mathcal{F}}_2)$
. Let
$\xi ({\mathcal{F}}_1)=\xi ({\mathcal{F}}_2)$
. Let
![]() $F = E\backslash R({\mathcal{F}}_1)$
. Then
$F = E\backslash R({\mathcal{F}}_1)$
. Then
![]() $\pi _{{\mathcal{F}}_1}$
and
$\pi _{{\mathcal{F}}_1}$
and
![]() $\pi _{{\mathcal{F}}_2}$
have the same projection on
$\pi _{{\mathcal{F}}_2}$
have the same projection on
![]() $F$
, meaning that for any partial configuration
$F$
, meaning that for any partial configuration
![]() ${\mathcal{A}}\in \Omega _F$
,
${\mathcal{A}}\in \Omega _F$
,
![]() $\pi _{{\mathcal{F}}_1}({\mathcal{F}}_1 \cup{\mathcal{A}}) = \pi _{{\mathcal{F}}_2}({\mathcal{F}}_2 \cup{\mathcal{A}})$
.
$\pi _{{\mathcal{F}}_1}({\mathcal{F}}_1 \cup{\mathcal{A}}) = \pi _{{\mathcal{F}}_2}({\mathcal{F}}_2 \cup{\mathcal{A}})$
.
Proof. Let
![]() $\mathcal{A}$
be a partial configuration in
$\mathcal{A}$
be a partial configuration in
![]() $\Omega _F$
. Consider the components of
$\Omega _F$
. Consider the components of
![]() $G[{\mathrm{In}}({\mathcal{F}}_1\cup{\mathcal{A}})]$
and
$G[{\mathrm{In}}({\mathcal{F}}_1\cup{\mathcal{A}})]$
and
![]() $G[{\mathrm{In}}({\mathcal{F}}_2\cup{\mathcal{A}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}_2\cup{\mathcal{A}})]$
.
-
• The components of
 $G[{\mathrm{In}}({\mathcal{F}}_1\cup{\mathcal{A}})]$
containing only vertices of
$G[{\mathrm{In}}({\mathcal{F}}_1\cup{\mathcal{A}})]$
containing only vertices of
 $V_R({\mathcal{F}}_1)\backslash \partial{\mathcal{F}}_1$
do not depend on the partial configuration
$V_R({\mathcal{F}}_1)\backslash \partial{\mathcal{F}}_1$
do not depend on the partial configuration
 $\mathcal{A}$
. Let
$\mathcal{A}$
. Let
 $C_1$
be the number of these components. Similarly, the components of
$C_1$
be the number of these components. Similarly, the components of
 $G[{\mathrm{In}}({\mathcal{F}}_2 \cup{\mathcal{A}})]$
containing only vertices of
$G[{\mathrm{In}}({\mathcal{F}}_2 \cup{\mathcal{A}})]$
containing only vertices of
 $V_R({\mathcal{F}}_2) \backslash \partial{\mathcal{F}}_2$
do not depend on
$V_R({\mathcal{F}}_2) \backslash \partial{\mathcal{F}}_2$
do not depend on
 $\mathcal{A}$
. Let
$\mathcal{A}$
. Let
 $C_2$
be the number of these components.
$C_2$
be the number of these components. -
• The components of
 $G[{\mathrm{In}}({\mathcal{F}}_1\cup{\mathcal{A}})]$
containing only vertices of
$G[{\mathrm{In}}({\mathcal{F}}_1\cup{\mathcal{A}})]$
containing only vertices of
 $V\backslash V_R({\mathcal{F}}_1)$
depend on
$V\backslash V_R({\mathcal{F}}_1)$
depend on
 $\mathcal{A}$
but not on
$\mathcal{A}$
but not on
 $F$
, so the same components are in
$F$
, so the same components are in
 $G[{\mathrm{In}}({\mathcal{F}}_2\cup{\mathcal{A}})]$
.
$G[{\mathrm{In}}({\mathcal{F}}_2\cup{\mathcal{A}})]$
. -
• Since
 $\xi ({\mathcal{F}}_1) = \xi ({\mathcal{F}}_2)$
, there is one-to-one correspondence between components of
$\xi ({\mathcal{F}}_1) = \xi ({\mathcal{F}}_2)$
, there is one-to-one correspondence between components of
 $G[{\mathrm{In}}({\mathcal{F}}_1 \cup{\mathcal{A}})]$
that contain vertices in
$G[{\mathrm{In}}({\mathcal{F}}_1 \cup{\mathcal{A}})]$
that contain vertices in
 $\partial{\mathcal{F}}_1$
and components of
$\partial{\mathcal{F}}_1$
and components of
 $G[{\mathrm{In}}({\mathcal{F}}_2 \cup{\mathcal{A}})]$
containing vertices in
$G[{\mathrm{In}}({\mathcal{F}}_2 \cup{\mathcal{A}})]$
containing vertices in
 $\partial{\mathcal{F}}_2$
. Any two components that correspond to each other induce the same component on
$\partial{\mathcal{F}}_2$
. Any two components that correspond to each other induce the same component on
 $F$
.
$F$
.
Thus, for any
![]() ${\mathcal{A}} \colon F \rightarrow \{0,1,*\}$
, the number of components in
${\mathcal{A}} \colon F \rightarrow \{0,1,*\}$
, the number of components in
![]() $G[{\mathrm{In}}({\mathcal{A}} \cup{\mathcal{F}}_1)]$
minus
$G[{\mathrm{In}}({\mathcal{A}} \cup{\mathcal{F}}_1)]$
minus
![]() $C_1$
is equal to the number of components in
$C_1$
is equal to the number of components in
![]() $G[{\mathrm{In}}({\mathcal{A}} \cup{\mathcal{F}}_2)]$
minus
$G[{\mathrm{In}}({\mathcal{A}} \cup{\mathcal{F}}_2)]$
minus
![]() $C_2$
. Hence
$C_2$
. Hence
![]() $w_G({\mathcal{A}}\cup{\mathcal{F}}_1)$
and
$w_G({\mathcal{A}}\cup{\mathcal{F}}_1)$
and
![]() $w_G({\mathcal{A}}\cup{\mathcal{F}}_2)$
differ by a constant multiplicative factor, from which the result follows.
$w_G({\mathcal{A}}\cup{\mathcal{F}}_2)$
differ by a constant multiplicative factor, from which the result follows.
Cor 53 gives information about marginals in the case where
![]() $R({\mathcal{F}}_1) = R({\mathcal{F}}_2)$
and
$R({\mathcal{F}}_1) = R({\mathcal{F}}_2)$
and
![]() ${\mathrm{In}}({\mathcal{F}}_1) \subseteq{\mathrm{In}}({\mathcal{F}}_2)$
. The proof follows from Observation52.
${\mathrm{In}}({\mathcal{F}}_1) \subseteq{\mathrm{In}}({\mathcal{F}}_2)$
. The proof follows from Observation52.
Observation 52.
Let
![]() $f$
be an edge in
$f$
be an edge in
![]() $E$
. Consider partial configurations
$E$
. Consider partial configurations
![]() ${\mathcal{F}}_1$
and
${\mathcal{F}}_1$
and
![]() ${\mathcal{F}}_2$
with
${\mathcal{F}}_2$
with
![]() $R({\mathcal{F}}_1) = R({\mathcal{F}}_2)= E\backslash \{f\}$
and
$R({\mathcal{F}}_1) = R({\mathcal{F}}_2)= E\backslash \{f\}$
and
![]() ${\mathrm{In}}({\mathcal{F}}_1) \subseteq{\mathrm{In}}({\mathcal{F}}_2)$
. Let
${\mathrm{In}}({\mathcal{F}}_1) \subseteq{\mathrm{In}}({\mathcal{F}}_2)$
. Let
![]() ${\mathcal{A}}_1 \sim \pi _{{\mathcal{F}}_1}$
and
${\mathcal{A}}_1 \sim \pi _{{\mathcal{F}}_1}$
and
![]() ${\mathcal{A}}_2 \sim \pi _{{\mathcal{F}}_2}$
. Then
${\mathcal{A}}_2 \sim \pi _{{\mathcal{F}}_2}$
. Then
![]() ${\mathbb{P}}( f\in{\mathrm{In}}({\mathcal{A}}_1)) \leq{\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_2))$
.
${\mathbb{P}}( f\in{\mathrm{In}}({\mathcal{A}}_1)) \leq{\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_2))$
.
Proof. First, observe that if
![]() $G[{\mathrm{In}}({\mathcal{F}}_1)]$
has two components connected by
$G[{\mathrm{In}}({\mathcal{F}}_1)]$
has two components connected by
![]() $f$
then the vertices in these components are connected in
$f$
then the vertices in these components are connected in
![]() $G[{\mathrm{In}}({\mathcal{F}}_2)\cup \{f\}]$
.
$G[{\mathrm{In}}({\mathcal{F}}_2)\cup \{f\}]$
.
For
![]() $j\in \{0,1\}$
, let
$j\in \{0,1\}$
, let
![]() ${\mathcal{F}}_{i,j}$
be
${\mathcal{F}}_{i,j}$
be
![]() ${\mathcal{F}}_i\cup \{f\mapsto j\}$
. Then, by the observation,
${\mathcal{F}}_i\cup \{f\mapsto j\}$
. Then, by the observation,
![]() $c({\mathcal{F}}_{2,0})-c({\mathcal{F}}_{2,1})\leq c({\mathcal{F}}_{1,0})-c({\mathcal{F}}_{1,1})$
. It follows that
$c({\mathcal{F}}_{2,0})-c({\mathcal{F}}_{2,1})\leq c({\mathcal{F}}_{1,0})-c({\mathcal{F}}_{1,1})$
. It follows that
 \begin{align*}{\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_1)) &= \frac{{\mathbb{P}}({\mathcal{F}}_{1,1})}{{\mathbb{P}}({\mathcal{F}}_{1,1})+{\mathbb{P}}({\mathcal{F}}_{1,0})} = \frac{(e^\beta -1)^{|{\mathcal{F}}_{1}^{-1}(1)|+1} q^{c({\mathcal{F}}_{1,1})}}{ (e^\beta -1)^{|{\mathcal{F}}_{1}^{-1}(1)|+1} q^{c({\mathcal{F}}_{1,1})} + (e^\beta -1)^{|{\mathcal{F}}_{1}^{-1}(1)|} q^{c({\mathcal{F}}_{1,0})}} \\[5pt] &= \frac{(e^\beta -1)q^{c({\mathcal{F}}_{1,1})-c({\mathcal{F}}_{1,0})}}{(e^\beta -1)q^{c({\mathcal{F}}_{1,1})-c({\mathcal{F}}_{1,0})} + 1} \leq \frac{(e^\beta -1)q^{c({\mathcal{F}}_{2,1})-c({\mathcal{F}}_{2,0})}}{(e^\beta -1)q^{c({\mathcal{F}}_{2,1})-c({\mathcal{F}}_{2,0})} + 1} \\[5pt] &={\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_2)) \end{align*}
\begin{align*}{\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_1)) &= \frac{{\mathbb{P}}({\mathcal{F}}_{1,1})}{{\mathbb{P}}({\mathcal{F}}_{1,1})+{\mathbb{P}}({\mathcal{F}}_{1,0})} = \frac{(e^\beta -1)^{|{\mathcal{F}}_{1}^{-1}(1)|+1} q^{c({\mathcal{F}}_{1,1})}}{ (e^\beta -1)^{|{\mathcal{F}}_{1}^{-1}(1)|+1} q^{c({\mathcal{F}}_{1,1})} + (e^\beta -1)^{|{\mathcal{F}}_{1}^{-1}(1)|} q^{c({\mathcal{F}}_{1,0})}} \\[5pt] &= \frac{(e^\beta -1)q^{c({\mathcal{F}}_{1,1})-c({\mathcal{F}}_{1,0})}}{(e^\beta -1)q^{c({\mathcal{F}}_{1,1})-c({\mathcal{F}}_{1,0})} + 1} \leq \frac{(e^\beta -1)q^{c({\mathcal{F}}_{2,1})-c({\mathcal{F}}_{2,0})}}{(e^\beta -1)q^{c({\mathcal{F}}_{2,1})-c({\mathcal{F}}_{2,0})} + 1} \\[5pt] &={\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_2)) \end{align*}
where the inequality follows from
![]() $c({\mathcal{F}}_{1,1})-c({\mathcal{F}}_{1,0})\leq c({\mathcal{F}}_{2,1})-c({\mathcal{F}}_{2,0})$
.
$c({\mathcal{F}}_{1,1})-c({\mathcal{F}}_{1,0})\leq c({\mathcal{F}}_{2,1})-c({\mathcal{F}}_{2,0})$
.
In the language of [Reference Grimmett18], Observation52 says that
![]() $\pi$
is
$\pi$
is
![]() $1$
-monotonic. It implies the following monotonicity result.
$1$
-monotonic. It implies the following monotonicity result.
Corollary 53.
Let
![]() $f$
be an edge of
$f$
be an edge of
![]() $E$
. Consider partial configurations
$E$
. Consider partial configurations
![]() ${\mathcal{F}}_1$
and
${\mathcal{F}}_1$
and
![]() ${\mathcal{F}}_2$
with
${\mathcal{F}}_2$
with
![]() $R({\mathcal{F}}_1) = R({\mathcal{F}}_2)$
and
$R({\mathcal{F}}_1) = R({\mathcal{F}}_2)$
and
![]() ${\mathrm{In}}({\mathcal{F}}_1) \subseteq{\mathrm{In}}({\mathcal{F}}_2)$
. Let
${\mathrm{In}}({\mathcal{F}}_1) \subseteq{\mathrm{In}}({\mathcal{F}}_2)$
. Let
![]() ${\mathcal{A}}_1 \sim \pi _{{\mathcal{F}}_1}$
and
${\mathcal{A}}_1 \sim \pi _{{\mathcal{F}}_1}$
and
![]() ${\mathcal{A}}_2 \sim \pi _{{\mathcal{F}}_2}$
. Then
${\mathcal{A}}_2 \sim \pi _{{\mathcal{F}}_2}$
. Then
![]() ${\mathbb{P}}( f\in{\mathrm{In}}({\mathcal{A}}_1)) \leq{\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_2))$
.
${\mathbb{P}}( f\in{\mathrm{In}}({\mathcal{A}}_1)) \leq{\mathbb{P}}(f\in{\mathrm{In}}({\mathcal{A}}_2))$
.
Proof. Use [Reference Grimmett18, Theorem 2.27]. It says that if a RCM measure is
![]() $1$
-monotonic, then the measure is monotonic, that is,
$1$
-monotonic, then the measure is monotonic, that is,
![]() $\pi _{{\mathcal{F}}_1}(A) \leq \pi _{{\mathcal{F}}_2}(A)$
for any increasing event – that is any
$\pi _{{\mathcal{F}}_1}(A) \leq \pi _{{\mathcal{F}}_2}(A)$
for any increasing event – that is any
![]() $A\subseteq \Omega$
such that whenever
$A\subseteq \Omega$
such that whenever
![]() ${\mathcal{F}}'_{\!\!1},{\mathcal{F}}'_{\!\!2}$
are configurations with
${\mathcal{F}}'_{\!\!1},{\mathcal{F}}'_{\!\!2}$
are configurations with
![]() ${\mathrm{In}}({\mathcal{F}}'_{\!\!1})\subseteq{\mathrm{In}}({\mathcal{F}}'_{\!\!2})$
and
${\mathrm{In}}({\mathcal{F}}'_{\!\!1})\subseteq{\mathrm{In}}({\mathcal{F}}'_{\!\!2})$
and
![]() ${\mathcal{F}}'_{\!\!1}\in A$
, then also
${\mathcal{F}}'_{\!\!1}\in A$
, then also
![]() ${\mathcal{F}}'_{\!\!2}\in A$
.
${\mathcal{F}}'_{\!\!2}\in A$
.
Observation52 says that
![]() $\pi$
is
$\pi$
is
![]() $1$
-monotonic, thus monotonicity follows by the theorem. To conclude, take
$1$
-monotonic, thus monotonicity follows by the theorem. To conclude, take
![]() $A$
to be the increasing event ‘
$A$
to be the increasing event ‘
![]() $f$
is occupied’ – we can see that this is increasing as whenever, for configurations
$f$
is occupied’ – we can see that this is increasing as whenever, for configurations
![]() ${\mathcal{F}}'_{\!\!1},{\mathcal{F}}'_{\!\!2}$
,
${\mathcal{F}}'_{\!\!1},{\mathcal{F}}'_{\!\!2}$
,
![]() $f\in{\mathrm{In}}({\mathcal{F}}'_{\!\!1})$
, and
$f\in{\mathrm{In}}({\mathcal{F}}'_{\!\!1})$
, and
![]() ${\mathrm{In}}({\mathcal{F}}'_{\!\!1})\subseteq{\mathrm{In}}({\mathcal{F}}'_{\!\!2})$
, then also
${\mathrm{In}}({\mathcal{F}}'_{\!\!1})\subseteq{\mathrm{In}}({\mathcal{F}}'_{\!\!2})$
, then also
![]() $f\in{\mathrm{In}}({\mathcal{F}}'_{\!\!2})$
.
$f\in{\mathrm{In}}({\mathcal{F}}'_{\!\!2})$
.