No CrossRef data available.
Article contents
Projecting Difference Sets on the Positive Orthant
Published online by Cambridge University Press: 01 September 2008
Abstract
Let n ≥ 1 be an integer. Given a vector a=(a1,. . ,an)∈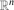 , write
, write
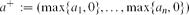 (the ‘projection of a onto the positive orthant’). For a set A⊆
(the ‘projection of a onto the positive orthant’). For a set A⊆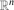 put A+:={a+: a ∈ A} and A−A:={a−b: a, b ∈ A}. Improving previously known bounds, we show that |(A−A)+| ≥ |A|3/5/6 for any finite set A⊆
put A+:={a+: a ∈ A} and A−A:={a−b: a, b ∈ A}. Improving previously known bounds, we show that |(A−A)+| ≥ |A|3/5/6 for any finite set A⊆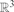 , and that |(A−A)+| ≥ c|A|6/11/(log |A|)2/11 with an absolute constant c>0 for any finite set A⊆
, and that |(A−A)+| ≥ c|A|6/11/(log |A|)2/11 with an absolute constant c>0 for any finite set A⊆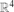 such that |A| ≥ 2.
such that |A| ≥ 2.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
[1]Balasubramanian, R. and Soundararajan, K. (1996) On a conjecture of R. L. Graham. Acta Arith. 75 1–38.CrossRefGoogle Scholar
[2]Granville, A. and Roesler, F. (1999) The set of differences of a given set. Amer. Math. Monthly 106 338–344.CrossRefGoogle Scholar
[3]Marica, J. and Schönheim, J. (1969) Differences of sets and a problem of Graham. Canad. Math. Bull. 12 635–637.CrossRefGoogle Scholar


